Главная /
Программирование /
Дискретная математика
Дискретная математика - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Дискретная математика - одна из важнейших составляющих современной математики. С одной стороны, она включает фундаментальные основы математики - теорию множеств, математическую логику, теорию алгоритмов; с другой стороны, является основным математическим аппаратом информатики и вычислительной техники и потому служит базой для многочисленных приложений в экономике, технике, социальной сфере.
Все ответы: Дискретная математика - одна из важнейших составляющих современной математики. С одной стороны, она включает фундаментальные основы математики - теорию множеств, математическую логику, теорию алгоритмов; с другой стороны, является основным математическим аппаратом информатики и вычислительной техники и потому служит базой для многочисленных приложений в экономике, технике, социальной сфере.
Смотрите также:
Каково число логических функций от
3 переменных?
(1)
8
(2)
9
(3)
28
Существуют ли простые графы
без петель с
5 вершинами
со следующим набором степеней:
(1)
(1,2,3,4,5)
(2)
(1,2,3,3,5)
(3)
(1,2,3,3,4)
(4)
(2,2,3,3,4)
Даны множества
A = {a,b,d,e,f}, B = {b,c,e,g}, С = {a,d,f}.
Отметьте верное равенство:
(1)
С = A∩B
(2)
С = A\B
(3)
С = A∪B
(4)
С = B\A
Встретились
6 друзей, и каждый пожал руку каждому.
Сколько всего было рукопожатий?
(1)
6
(2)
12
(3)
15
(4)
30
Какие из множеств замкнуты относительно сложения?
(1)
множество натуральных чисел
(2)
множество нечетных чисел
(3)
множество квадратных корней из натуральных чисел
(4)
множество натуральных чисел, кратных
3
В таблице приведены три функции
Какие из этих функций содержат несущественные переменные?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 0 |
0 | 1 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 1 |
1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 0 |
1 | 1 | 1 | 0 | 0 | 1 |
(1)
f1
(2)
f2
(3)
f3
Сколько ребер могут иметь простые графы без петель
с
5 вершинами?
(1)
одно ребро
(2)
5 ребер
(3)
10 ребер
(4)
25 ребер
Множество
A содержит 5 элементов,
множество B содержит 8 элементов. Сколько элементов может содержать их пересечение?
(1)
8 элементов
(2)
6 элементов
(3)
5 элементов
(4)
3 элемента
Сколькими способами можно выбрать гласную и согласную буквы
из слова «схема»?
(1)
5
(2)
6
(3)
12
(4)
25
Какие из операций ассоциативны?
(1)
вычитание чисел
(2)
сложение чисел
(3)
разность множеств
Какие из функций ассоциативны?
(1)
импликация
(2)
конъюнкция
(3)
штрих Шеффера?
Какой радиус может быть у графа
с
5 вершинами?
(1)
1
(2)
2
(3)
3
(4)
5
Множества ![math]()
, ![math]()
, ![math]()
выражены через три других множества
![math]()
, ![math]()
, ![math]()
следующими равенствами: ![math]()
, ![math]()
, ![math]()
.
Отметьте верное равенство:
, 
, 
выражены через три других множества
, 
, 
следующими равенствами: 
, 
, 
.
Отметьте верное равенство:
(1)
![math]()
(2)
![math]()
(3)
![math]()
В группе из
17 человек
английский язык изучают 10 человек,
французский язык изучают 6 человек
и оба языка изучают 2 человека.
Сколько человек в группе не изучает
ни английский, ни французский языки?
(1)
1
(2)
2
(3)
3
(4)
6
Какие из операций коммутативны?
(1)
вычитание чисел
(2)
умножение чисел
(3)
пересечение множеств
Какая из формул эквивалентна формуле
(¬x&y)∨(x&z)∨(¬x&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(¬x∨z)&(y∨z)
(3)
(x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с
5 вершинами?
(1)
3
(2)
4
(3)
5
(4)
6
Чему равна проекция множества
A = {(1,2),(1,3),(2,3),(3,4)} на первую координату?
(1)
{1,2,3,4}
(2)
{1,2,3}
(3)
{2,3,4}
На вершину горы ведут пять дорог.
Сколькими способами турист может подняться на гору
и спуститься с нее?
(1)
5
(2)
10
(3)
25
(4)
100
Какие из операций над множествами ассоциативны?
(1)
объединение
(2)
пересечение
(3)
разность
Функция
Какой из полиномов Жегалкина ей соответствует?
f задана таблицей:
x | y | z | f |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
(1)
xyz⊕xz⊕x⊕y⊕z
(2)
xyz⊕yz⊕x⊕z
(3)
xy⊕xz⊕y⊕z
(4)
xz⊕x⊕y⊕z
Какие из графов, приведенных на рисунке,
являются эйлеровыми?
![files]()
(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие
G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(c,4),(e,3)}.
Какое из множеств является образом элемента b при этом соответствии?
(1)
{1,2,3,4}
(2)
{1,4}
(3)
{2,3}
Сколькими способами можно составить
трехцветный полосатый флаг, если имеется материал
пяти различных цветов?
(1)
5
(2)
20
(3)
60
(4)
125
Отметьте подмножества, которые в алгебре целых чисел со сложением
образуют подалгебру:
(1)
множество чисел, кратных
5
(2)
множество
[0,1]
(3)
множество натуральных чисел
Какие из функций являются монотонными?
(1) конъюнкция
(2) импликация
(3) штрих Шеффера
Граф задан матрицей смежности:
Отметьте каким он является:
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
(4)
несвязным
Соответствие
G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(d,3)}.
Отметьте верное утверждение:
(1)
G всюду определено;
(2)
G функционально;
(3)
G сюръективно?
Сколько различных слов можно получить
перестановками букв в слове
abcd?
(1)
4
(2)
12
(3)
24
(4)
256
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
четные числа с операцией сложения
(2)
целые числа с операцией вычитания
(3)
рациональные числа с операцией умножения
(4)
множество
{-1,1} с операцией умножения
Какая из функций является линейной?
(1) эквивалентность
(2) стрелка Пирса
(3) конъюнкция
Отметьте графы, в которых возможна топологическая сортировка:
(1)
сильно связные
(2)
односторонне связным
(3)
слабо связные
(4)
несвязные
Какие из множеств являются счетными?
(1) множество натуральных чисел;
(2) множество рациональных чисел;
(3) множество действительных чисел;
(4)
множество
[0,1]
Сколькими способами можно выбрать три различные краски из имеющихся пяти (порядок красоок важен)?
(1)
3
(2)
60
(3)
15
(4)
35
Какие из множеств с операцией сложения образуют группу?
(1)
целые числа, кратные
3
(2)
множество
{-1,1}
(3)
неотрицательные целые числа
(4)
целые числа
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
дизъюнкция и сложение по модулю
2
(2)
импликация
(3)
эквивалентность и сложение по модулю
2
(4)
конъюнкция и дизъюнкция
Какую длину может иметь максимальный путь
в ациклическом графе с
n вершинами?
(1)
1
(2)
2
(3)
n-1
(4)
n
Между множествами
A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(c,3),(d,3),(d,4)}
и H = {(a,2),(b,1),(c,3),(d,3)}.
Какое соответствие функционально?
(1)
G и H
(2)
только
G
(3)
только
H
(4)
ни
G, ни H
В палитре художника
5 различных красок.
Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане.
Затем берет следующую кисть, окунает ее в любую из красок и делает второе пятно по соседству.
Сколько различных комбинаций существует для трех пятен? Порядок пятен на ватмане не важен?
(1)
10
(2)
25
(3)
35
(4)
125
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
множество
{-1,1} с операцией умножения
(2)
рациональные числа с операцией умножения
(3)
неотрицательные целые числа с операцией сложения
(4)
четные числа с операцией сложения
В таблице приведены три функции
Какие из этих функций функционально полны в слабом смысле?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 0 | 0 | 1 |
1 | 1 | 1 | 1 | 1 | 1 |
(1)
f1
(2)
f2
(3)
f3
Каким может быть ориентированное дерево?
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
Функция
f(x1,x2) имеет тип A2*B,
функция g(y1,y2) имеет тип CA*A.
Какой тип имеет функция f(x1,g(y1,y2))?
(1)
A2*B
(2)
CA*A
(3)
ACA*B
(4)
A2CA*B Какими из следующих
свойств обладают биномиальные коэффициенты?
(1)
Cnn-k=Cnk
(2)
![math]()
(3)
C2nn=(n!)2
Чему равен единичный элемент в группе целых чисел со сложением?
(1)
его не существует
(2)
0
(3)
1
Дано равенство
∀x∀yP(x,y) = ∃x∃yP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых
Р.
(2)
Это равенство верно при любых
Р.
(3)
Это равенство при некоторых
Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны ![files]()
Нарушены ли в ней правила распределения потоков?
4:
Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
Между точками горизонтальной прямой задано отношение «левее»
(
x левее y). Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины
5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово bcacd?
(1)
214
(2)
395
(3)
618
(4)
732
Какой элемент является образующей в группе целых чисел со сложением?
(1)
такого элемента не существует
(2)
0
(3)
1
Какая из формул исчисления предикатов выражает
тот факт, что в множестве
М, в котором определен
частичный порядок, не существует максимального элемента?
(1)
∀x∃y(x∈M→((y∈M)&(x<y)))
(2)
∀x∃y((x∈M)&(y∈M)&(x<y))
(3)
∀x∃y((x∈M)∨((y∈M)&(x<y)))
Граф является двудольным, если он ...
(1) имеет цикл с четным числом вершин
(2) имеет цикл с нечетным числом вершин
(3) ациклический граф
Объединение двух отношений частичного порядка будет отношением частичного порядка ...
(1) всегда
(2) иногда (может быть, а может не быть)
(3) никогда
Чему равно число таблиц размером
23
с элементами из множества мощности 3?
(1)
120
(2)
216
(3)
729
(4)
801
Чему равна наименьшая верхняя грань для ![files]()
{c,e}?
(1)
a
(2)
c
(3)
b
Отметьте неверную формулу:
(1)
∀x∀yP(x,y) = ∀y∀xP(x,y)
(2)
∀x∃yP(x,y) = ∃y∀xP(x,y)
(3)
∀x(P(x)&Q(x)) = ∀xP(x)&∀xQ(x).
Степень
Cn
матрицы смежности C
ориентированного графа G
содержит ненулевые элементы во всех
клетках главной диагонали если:
(1)
все вершины G имеют петли
(2)
некоторые вершины G имеют петли
(3)
граф G содержит циклы
(4)
граф G - сильно связный
На множестве
A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(a,c),(b,c),(c,d)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(d,a)
(2)
(a,d), (b,d)
(3)
никакие, так как
R транзитивно;
(4)
(a,d)
Даны три множества:
A = {a,b,c},
B = {-1,1}, C = {0,1}.
Каково число различных функций типа AB*C2?
(1)
24
(2)
64
(3)
46
(4)
10
Чему равна наибольшая нижняя грань для ![files]()
{b,d}?
(1)
e
(2)
f
(3)
g
Каково число логических функций от
4 переменных?
(1)
8
(2)
16
(3)
216
Существуют ли простые графы
без петель с
4 вершинами
со следующим набором степеней:
(1)
(1,2,3,4)
(2)
(1,2,3,3)
(3)
(1,2,2,3)
(4)
(1,1,2,3)
Даны множества ![math]()
, ![math]()
, ![math]()
.
Отметьте верное равенство:
, 
, 
.
Отметьте верное равенство:
(1)
![math]()
(2)
![math]()
(3)
![math]()
(4)
![math]()
Сколько четных двузначных чисел можно составить из цифр
2,3,6,7,9 (каждую цифру в числе можно использовать только 1 раз)?
(1)
5
(2)
8
(3)
10
(4)
25 Какие из множеств замкнуты относительно умножения?
(1)
множество натуральных чисел
(2)
множество нечетных чисел
(3)
множество положительных чисел
(4)
множество отрицательных чисел
В таблице приведены три функции
Какие из этих функций содержат несущественные переменные?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 1 | 1 | 1 |
0 | 0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 0 | 1 | 1 |
0 | 1 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 1 |
(1)
f1
(2)
f2
(3)
f3
Сколько ребер могут иметь простые графы без петель
с
6 вершинами?
(1)
одно ребро
(2)
6 ребер
(3)
15 ребер
(4)
36 ребер
Множество
A содержит 6 элементов,
множество B содержит 7 элементов. Сколько элементов может содержать их объединение?
(1)
9 элементов
(2)
7 элементов
(3)
6 элементов
(4)
4 элемента
Сколькими способами можно выбрать гласную и согласную буквы
из слова «здание»?
(1)
6
(2)
9
(3)
18
(4)
24
Какие из операций ассоциативны?
(1)
умножение чисел
(2)
объединение множеств
(3)
деление чисел
Какие из функций ассоциативны?
(1)
дизъюнкция
(2)
стрелка Пирса
(3)
сложение по модулю
2
Какой радиус может быть у графа
с
4 вершинами?
(1)
1
(2)
2
(3)
3
(4)
4
Множества
A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D\(E∪F), B = DE∪DF, C = (D\E)∩(D\F).
Отметьте верное равенство:
(1)
A=B
(2)
B=C
(3)
A=C
В группе из
15 человек
6 человек увлекаются театром,
8 человек увлекаются спортом
и 3 человека увлекаются и театром, и спортом.
Сколько человек в группе не увлекаются
ни театром, ни спортом?
(1)
1
(2)
3
(3)
4
(4)
14
Какие из операций коммутативны?
(1)
сложение чисел
(2)
пересечение множеств
(3)
разность множеств
Какая из формул эквивалентна формуле
(x&¬y)∨(y&z)∨(¬y&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(x∨z)&(¬y∨z)
(3)
(¬x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с
4 вершинами?
(1)
2
(2)
3
(3)
4
(4)
5
Чему равна проекция множества
A = {(1,3),(2,3),(2,4),(3,1)} на вторую координату?
(1)
{1,2,3,4}
(2)
{1,2,2,1}
(3)
{1,3,4,1}
(4)
{3,3,4,1}
Надо послать
4 срочных письма.
Сколькими способами можно это сделать, если для передачи
писем можно послать трех курьеров и каждое письмо
можно дать любому из курьеров?
(1)
3
(2)
4
(3)
12
(4)
24
Какие из операций над множествами коммутативны?
(1)
объединение
(2)
пересечение
(3)
разность
Функция
Какой из полиномов Жегалкина ей соответствует?
f задана таблицей:
x | y | z | f |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
(1)
xyz⊕xy⊕yz⊕z
(2)
xyz⊕yz⊕x⊕z
(3)
xy⊕yz⊕y⊕z
(4)
xz⊕x⊕y⊕1
Какие из графов, приведенных на рисунке,
являются эйлеровыми?
![files]()
(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие
G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(a,3),(b,3),(c,1),(e,3),(e,4)}.
Какое из множеств является прообразом элемента 3 при этом соответствии?
(1)
{a,b,c,e}
(2)
{a,b,e}
(3)
{a,c}
В группе из
20
человек нужно выбрать старосту и профорга.
Сколькими способами это можно сделать?
(1)
20
(2)
40
(3)
380
(4)
400
Отметьте подмножества, которые в алгебре целых чисел с умножением
образуют подалгебру:
(1)
множество чисел, кратных
3
(2)
множество
[0,1]
(3)
множество отрицательных чисел
Какие из функций являются монотонными?
(1)
отрицание
(2)
сложение по модулю
2
(3)
дизъюнкция
Отметьте каким является граф заданный матрицей смежности:
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
(1) сильно связным
(2) односторонне связным
(3) несвязным
(4) слабо связным
Соответствие
G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,1),(d,4)}.
Отметьте верные утверждения:
(1)
G всюду определено
(2)
G функционально
(3)
G обратимо
(4)
G взаимно однозначно
Сколько различных слов можно получить
перестановками букв в слове
abcde?
(1)
5
(2)
20
(3)
120
(4)
55
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
неотрицательные целые числа с операцией сложения
(2)
нечетные числа с операцией сложения
(3)
положительные рациональные числа с операцией умножения
(4)
нечетные числа с операцией умножения
Какие из функций являются линейными?
(1)
сложение по модулю
2
(2)
штрих Шеффера
(3)
дизъюнкция
(4)
константа
Какие графы могут совпадать со своим
графом конденсации?
(1)
сильно связным;
(2)
односторонне связным;
(3)
слабо связным;
(4)
несвязным?
Какое из множеств является конечным?
(1) множество всех натуральных чисел;
(2) множество всех рациональных чисел;
(3) действительные числа отрезка
[0,1]
(4) множество
{1,2,3} Сколькими способами из
10
спортсменов можно отобрать команду из 6 человек?
(1)
C106
(2)
60
(3)
A106
(4)
610
Какие из множеств с операцией сложения образуют группу?
(1)
нечетные числа
(2)
рациональные числа
(3)
множество
[-1,1]
(4)
целые числа, имеющие остаток от деления на
4, равный 3
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
дизъюнкция и отрицание
(2)
штрих Шеффера
(3)
эквивалентность и отрицание
(4)
конъюнкция и импликация
Дан ациклический граф с
n вершинами.
Сколько в нем может быть вершин, которые не являются ни источниками, ни стоками?
(1)
n
(2)
n+1
(3)
n2
(4)
n-2
Между множествами
A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(a,1),(b,1),(c,3),(d,4)}
и H = {(a,1),(c,1),(c,3),(d,4)}.
Какое соответствие функционально?
(1)
G и H
(2)
только
G
(3)
только
H
(4)
ни
G, ни H
В кондитерском магазине продавались три сорта пироженных:
эклеры, наполеоны и слоеные. Сколькими способами можно купить
4 пироженных?
(1)
4
(2)
9
(3)
12
(4)
15
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
степени двойки с целыми показателями с операцией умножения
(2)
рациональные числа с операцией сложения
(3)
положительные рациональные числа с операцией деления
(4)
нечетные числа с операцией сложения
В таблице приведены три функции
Какие из этих функций функционально полны в слабом смысле?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 1 | 0 |
0 | 1 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 |
(1)
f1
(2)
f2
(3)
f3
Сколько центров может быть у дерева
с
n вершинами?
(1)
1
(2)
2
(3)
n-1
(4)
n
Функция
f(x1,x2) имеет тип AB→C,
функция g(y1,y2) имеет тип AC→A.
Какой тип имеет функция f(g(y1,y2),x2)?
(1)
AB→C
(2)
AC→A
(3)
ACB→C
(4)
ABAC→C
Какими из следующих свойств обладают биномиальные коэффициенты?
(1)
Cnn-k=Cnk
(2) ![math]()
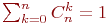
(3)
Cn+1k=Cnk+Cnk-1 Чему равен единичный элемент в группе целых степеней двойки с умножением?
(1)
его не существует
(2)
1
(3)
2
Дано равенство
∀x∃yP(x,y) = ∃x∀yP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых
Р.
(2)
Это равенство верно при любых
Р.
(3)
Это равенство при некоторых
Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны ![files]()
Нарушены ли в ней правила распределения потоков?
4:
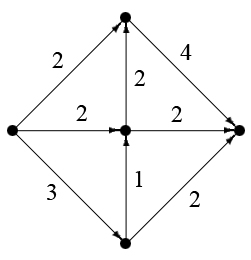Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
На множестве действительных чисел задано отношение
|x-y|<5.
Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины
5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово abcad?
(1)
84
(2)
99
(3)
125
(4)
212
Какой элемент является образующей в группе целых степеней двойки с умножением?
(1)
такого элемента не существует
(2)
1
(3)
2
Какая из формул исчисления предикатов выражает
тот факт, что в множестве
М, в котором определен
частичный порядок, не существует минимального элемента?
(1)
∀x∃y(x∈M→((y∈M)&(y<x)))
(2)
∀x∃y((x∈M)&(y∈M)&(y<x))
(3)
∀x∃y((x∈M)∨((y∈M)&(y<x)))
Во сколько цветов можно раскрасить цикл, содержащий
9 вершин?
(1)
в
2 цвета
(2)
в
3 цвета
(3)
в
4 цвета
Каким может быть дополнение к отношению эквивалентности?
(1) рефлексивным
(2) симметричным
(3) антисимметричным
Чему равно число таблиц размером
33
с элементами из множества мощности 2?
(1)
72
(2)
81
(3)
512
(4)
1024
Чему равна наименьшая верхняя грань для ![files]()
{c,g}?
(1)
a
(2)
c
(3)
d
Отметьте неверную формулу:
(1)
∀x(P(x)&Q(x)) = ∀xP(x)&∀xQ(x)
(2)
∃x(P(x)&Q(x)) = ∃xP(x)&∃xQ(x)
(3)
∃x∃yP(x,y) = ∃y∃xP(x,y).
Ориентированный граф
G содержит циклы.
Какое из утверждений всегда верно?
(1)
степень
Cn матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы во всех клетках главной диагонали
(2)
степень
Cn матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы во некоторых клетках главной диагонали
(3)
сумма ![math]()
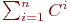степеней матрицы
смежности
степеней матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы в некоторых клетках главной диагонали
(4)
сумма ![math]()
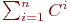степеней матрицы
смежности
степеней матрицы
смежности C ориентированного
графа G содержит ненулевые
элементы во всех клетках главной диагонали
На множестве
A = {a,b,c,d} задано бинарное отношение
R = {(a,d),(b,d),(d,c)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(c,d)
(2)
(a,c), (b,c)
(3)
никакие, так как
R транзитивно;
(4)
(a,b), (b,a)
Даны три множества:
A = {1,2,3},
B = {a,b}, C = {0,1}.
Каково число различных функций типа AB2→C?
(1)
24
(2)
144
(3)
212
(4)
512
Чему равна наибольшая нижняя грань для ![files]()
{e,g}?
(1)
c
(2)
f
(3)
h
Каково число логических функций от
5 переменных?
(1)
25
(2)
32
(3)
232
Существуют ли простые графы
без петель с
6 вершинами
со следующим набором степеней:
(1)
(1,2,3,4,5,6)
(2)
(1,2,3,4,5,5)
(3)
(1,2,3,4,4,5)
(4)
(1,3,3,3,3,5)
Даны множества
A = {a,b,d,e}, B = {b,c,e,f,g}, С = {c,f,g}.
Отметьте верное равенство:
(1)
С = A∩B
(2)
С = A\B
(3)
С = A∪B
(4)
С = B\A
Сколько нечетных двузначных чисел можно составить из цифр
1,2,5,7,8 (цифры можно использовать только 1 раз)?
(1)
5
(2)
12
(3)
15
(4)
25
Какие из множеств замкнуты относительно сложения?
(1)
множество положительных чисел
(2)
множество отрицательных чисел
(3)
множество целых степеней двойки
(4)
множество четных чисел
В таблице приведены три функции
Какие из этих функций содержат несущественные переменные?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 1 | 1 | 1 |
0 | 1 | 0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 | 1 | 0 |
1 | 0 | 0 | 1 | 1 | 0 |
1 | 0 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 1 |
1 | 1 | 1 | 1 | 1 | 0 |
(1)
f1
(2)
f2
(3)
f3
Сколько ребер могут иметь простые графы без петель
с
4 вершинами?
(1)
одно ребро
(2)
4 ребер
(3)
6 ребер
(4)
16 ребер
Множество
A содержит 5 элементов,
множество B содержит 8 элементов. Сколько элементов может содержать разность A\B?
(1)
0 элементов
(2)
2 элемента
(3)
5 элементов
(4)
8 элементов
Сколькими способами можно выбрать гласную и согласную буквы
из слова «пехота»?
(1)
6
(2)
9
(3)
15
(4)
36
Какие из операций ассоциативны?
(1)
возведение в степень
(2)
пересечение множеств
(3)
объединение множеств
Какие из функций ассоциативны?
(1)
эквивалентность
(2)
импликация
(3)
сложение по модулю
2
Какой радиус может быть у графа
с
6 вершинами?
(1)
1
(2)
2
(3)
3
(4)
5
Множества
A, B, C выражены через три других множества
D, E, F следующими равенствами
(знак пересечения опущен): A = D∪EF, B = ((D\E)∪E)F, С = DF∪EF.
Отметьте верное равенство:
(1)
A=B
(2)
B=C
(3)
A=C
В группе из
20 человек
5 человек сдали экзамен по истории на «отлично»,
7 человек сдали экзамен по высшей математике на «отлично»
и 2 человека сдали экзамен по обоим предметам на «отлично».
Сколько человек в группе не сдали на «отлично»
ни экзамен по истории, ни экзамен по высшей математике?
(1)
2
(2)
6
(3)
10
(4)
14
Какие из операций коммутативны?
(1)
деление чисел
(2)
возведение в степень
(3)
объединение множеств
Какая из формул эквивалентна формуле
(x&y)∨(y&z)∨(¬y&z)?
(1)
(x∨¬z)&(y∨z)
(2)
(x∨z)&(y∨z)
(3)
(¬x∨z)&(y∨z)
Какое расстояние между двумя вершинами возможно графе с
6 вершинами?
(1)
2
(2)
4
(3)
5
(4)
6
Чему равна проекция множества
A = {(1,4),(2,1),(2,3),(4,3)} на первую координату?
(1)
{1,2,3,4}
(2)
{1,2,4}
(3)
{1,3,4}
Трое студентов сдают экзамен.
Сколькими способами могут быть поставлены
им отметки, если известно, что никто
из них не получил неудовлетворительной
отметки?
(1)
3
(2)
9
(3)
27
(4)
81
Отметьте дистрибутивны слева множества:
(1)
объединение относительно пересечения
(2)
пересечение относительно разности
(3)
разность относительно объединения
Функция
Какой из полиномов Жегалкина ей соответствует?
f задана таблицей:
x | y | z | f |
|---|---|---|---|
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
(1)
xyz⊕xy⊕x⊕y⊕1
(2)
xyz⊕x⊕y⊕1
(3)
xy⊕x⊕y⊕z
(4)
xz⊕x⊕y⊕1
Какие из графов, приведенных на рисунке,
являются эйлеровыми?
![files]()
(1)
первый граф
(2)
второй граф
(3)
третий граф
Соответствие
G между множествами A = {a,b,c,d,e} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(b,1),(c,3),(d,1),(d,4),(e,3)}.
Какое из множеств является образом элемента d при этом соответствии?
(1)
{1,2,3,4}
(2)
{1,2,3}
(3)
{1,4}
В некоторых видов спортивных
соревнований исходом является определение
участников, занявших первое, второе и третье
места. В соревновании участвует
10
человек. Сколько возможно различных исходов?
(1)
10
(2)
30
(3)
720
(4)
1000
Отметьте подмножества, которые в алгебре действительных чисел с умножением
образуют подалгебру:
(1)
множество целых степеней двойки
(2)
множество
{0,1,2}
(3)
множество натуральных чисел
Какая из функций являются монотонной?
(1)
эквивалентность
(2)
стрелка Пирса
(3)
константа
Соответствие
G между множествами A = {a,b,c,d} и B = {1,2,3,4}
задано множеством пар G = {(a,2),(c,1),(c,3),(d,3),(d,4)}.
Отметьте верное утверждение:
(1)
G всюду определено;
(2)
G функционально;
(3)
G сюръективно?
Сколько различных слов можно получить
перестановками букв в слове
abc?
(1)
3
(2)
6
(3)
9
(4)
27
Какие из множеств с указанной операцией над элементами образуют полугруппу?
(1)
целые числа, кратные
7, с операцией сложения
(2)
положительные рациональные числа с операцией деления
(3)
степени двойки с целыми показателями с операцией умножения
(4)
целые числа с операцией сложения
Какие из функций являются линейными?
(1)
отрицание
(2)
константа
(3)
импликация
Каким может быть граф конденсации?
(1)
сильно связным
(2)
односторонне связным
(3)
слабо связным
(4)
несвязным
Какие из множеств имеют мощность континуума:
(1) множество натуральных чисел;
(2) множество рациональных чисел;
(3) множество действительных чисел;
(4) множество
[0,1]
Сколько существует двухэлементных
подмножеств множества
{a,b,c,d}?
(1)
4
(2)
6
(3)
12
(4)
16
Какие из множеств с операцией сложения образуют группу?
(1)
неотрицательные рациональные числа
(2)
целые степени двойки
(3)
целые числа, кратные
4
(4)
множество
{0} (состоящее только из нуля)
Какие из перечисленных систем функций функционально полны в слабом смысле?
(1)
стрелка Пирса
(2)
импликация и отрицание
(3)
сложение по модулю
2 и отрицание
(4)
импликация и дизъюнкция
Отметьте возможные длины максимального пути в ациклическом графе с
6 вершинами и 5 ребрами:
(1)
1
(2)
2
(3)
4
(4)
5
Между множествами
A = {a,b,c,d} и B = {1,2,3,4}
множеством пар заданы соответствия G = {(b,1),(c,2),(d,2),(d,3)}
и H = {(a,2),(b,2),(c,4),(d,1)}.
Какое соответствие функционально?
(1)
G и H
(2)
только
G
(3)
только
H
(4)
ни
G, ни H
В почтовом отделении имеются открытки
3 видов.
Сколькими способами можно купить набор из 5 открыток?
(1)
10
(2)
15
(3)
21
(4)
25
Какие из множеств с указанной операцией над элементами образуют группу?
(1)
целые числа с операцией вычитания
(2)
целые числа, кратные
3, с операцией сложения
(3)
рациональные числа, отличные от нуля, с операцией умножения
(4)
нечетные числа с операцией умножения
В таблице приведены три функции
Какие из этих функций функционально полны в слабом смысле?
f1,
f2, f3
от переменных x, y, z:
x | y | z | f1 | f2 | f3 |
|---|---|---|---|---|---|
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 | 1 |
1 | 0 | 1 | 1 | 0 | 1 |
1 | 1 | 0 | 1 | 1 | 0 |
1 | 1 | 1 | 1 | 1 | 1 |
(1)
f1
(2)
f2
(3)
f3
Сколько висячих вершин может быть у дерева
с
n вершинами?
(1)
1
(2)
2
(3)
n-1
Функция
f(x1,x2) имеет тип AC→B,
функция g(y1,y2) имеет тип AC→C.
Какой тип имеет функция f(x1,g(y1,y2))?
(1)
AC→B
(2)
AC→C
(3)
A2C→B
(4)
ACAC→C
Какими из следующих
свойств обладают биномиальные коэффициенты?
(1)
C2nn=Cn+1n
(2)
![math]()
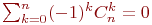
(3)
Cn+1k=Cnk+Cnk-1
Чему равен единичный элемент в группе
{-1,1} с умножением?
(1)
его не существует
(2)
1
(3)
-1
Дано равенство
∀x∃yP(x,y) = ∃y∀xP(x,y).
Какие из утверждений верны?
(1)
Это равенство неверно при любых
Р.
(2)
Это равенство верно при любых
Р.
(3)
Это равенство при некоторых
Р верно, а при некоторых других Р неверно.
В потоковой сети, приведенной на рисунке,
все пропускные способности равны ![files]()
Нарушены ли в ней правила распределения потоков?
4:
Нарушены ли в ней правила распределения потоков?
(1)
Нет, все верно.
(2)
Да, нарушен закон Кирхгофа.
(3)
Да, нарушено ограничение на пропускную способность.
На множестве натуральных чисел задано отношение «
x+y
делится на 2». Отметьте верное утверждение:
(1) отношение рефлексивно
(2) отношение антирефлексивно
(3) отношение симметрично
(4) отношение транзитивно
Слова длины
5 в алфавите {a,b,c,d}
перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0.
Какой номер будет иметь слово caabd?
(1)
625
(2)
519
(3)
812
(4)
907
Какой элемент является образующей в группе
{-1,1} с умножением?
(1)
такого элемента не существует
(2)
1
(3)
-1
Какая из формул исчисления предикатов выражает
тот факт, что в множестве
М, в котором определен
частичный порядок, существует максимальный элемент?
(1)
∃x∀y(((x∈M)&(y∈M)&(x<y))→(x=y))
(2)
∀x∃y(((x∈M)&(y∈M)&(x<y))→(x=y))
(3)
∃x∃y(((x∈M)&(y∈M)&(x<y))→(x=y))
Для любого
k число путей
длины k, начинающихся с любой вершины
графа G, всегда одинаково, если
(1)
G — неориентированное дерево
(2)
G — неориентированный цикл
(3)
G — полный граф
Каким может быть дополнение к отношению строгого порядка?
(1) рефлексивным
(2) симметричным
(3) антисимметричным
Чему равно число таблиц размером
3x2
с элементами из множества мощности 3?
(1)
216
(2)
256
(3)
512
(4)
729
Чему равна наименьшая верхняя грань для ![files]()
{b,f}?
(1)
a
(2)
b
(3)
d
Отметьте неверную формулу:
(1)
∀x∀yP(x,y) = ∀y∀xP(x,y)
(2)
∀x(P(x)∨Q(x)) = ∀xP(x)∨∀xQ(x)
(3)
∃x(P(x)∨Q(x)) = ∃xP(x)∨∃xQ(x).
На множестве
A = {a,b,c,d} задано бинарное отношение
R = {(a,b),(b,c),(b,d)}. Какие пары нужно добавить к R, чтобы
получить его транзитивное замыкание?
(1)
(a,c), (a,d)
(2)
(c,d), (d,c)
(3)
никакие, так как
R транзитивно;
(4)
(b,a)
Даны два множества:
A = {a,b,c},
B = {0,1}.
Каково число различных функций типа AB2→B2?
(1)
48
(2)
124
(3)
412
(4)
256
Чему равна наибольшая нижняя грань для ![files]()
{c,f}?
(1)
e
(2)
g
(3)
h