Основы аналитической геометрии - ответы на тесты Интуит
Все ответы: Курс состоит из 24-х двухчасовых лекций. Содержит сведения по аналитической геометрии; теории матриц; системам линейных алгебраических уравнений; линейным пространствам и операторам; элементам общей алгебры.
Найти координату проекции на ось ОХ точки А(4;6).
Найти скалярное произведение векторов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Условия.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:



Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Условия.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
Задано уравнение эллипса:
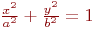
Значения  и
и 
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
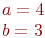 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 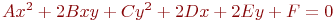 . Найти преобразование координат
. Найти преобразование координат 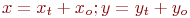 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
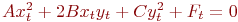 . Указать значение
. Указать значение 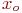 .
.
Ответ введите с точностью 2 знака после запятой.
Найти уравнение плоскости в виде  , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость ХОУ.
Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
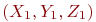 и прямую заданную уравнением:
и прямую заданную уравнением:
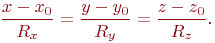 Уравнение представить в виде:
Уравнение представить в виде:
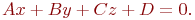
Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
Сколько общих точек имеют линии заданные уравнениями:
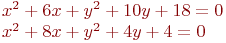
Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 
y=kx+b по координатам двух точек, через которые проходит прямая: (4;6) и (5;9).k=3; b=-6 k=-0,8; b=9,4 k=1,25; b=-4,25 k=2; b=-2 Найти решение системы уравнений методом Гаусса.
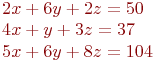
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 2 | 6 | 0 | 1 | 72 |
| 1 | -3 | -6 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 0 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.

Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
Найти их сумму.



Заданы координаты двух векторов: (6;9) и (3;2). Найти сумму векторов.
Найти координату проекции на ось ОУ точки А(4;6).
Даны два вектора.
Найти угол между ними (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Условия.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
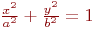
Значения  и
и 
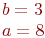
Какая из нижеприведенных точек лежит внутри этой кривой.



Даны полуоси гиперболы  и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
Задано уравнение кривой в виде: 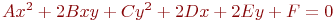 . Найти преобразование координат
. Найти преобразование координат 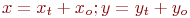 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
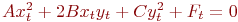 . Указать значение
. Указать значение 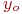 .
.
Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость УОZ.
Найти угол, под которым с плоскостью
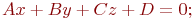
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
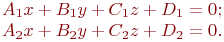
Составить уравнение плоскости проходящей через прямую уравнением:
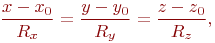
Параллельно прямой:
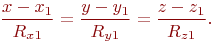
Уравнение представить в виде:
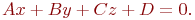
Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
Найти координаты центра линии.
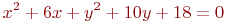
Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
Rx=1; Ry=3 Rx=5; Ry=-4 Rx=4; Ry=5 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И столбец свободных членов:
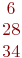
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 6 | 6 | 0 | 1 | 72 |
| 1 | -4 | -9 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.



Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их разность.
Заданы координаты двух векторов: (6;9) и (3;2). Найти разность векторов.
Найти координаты точки В, симметричной точке А(3;4) относительно оси ОХ.
(3;-4) (2;3) (6;-7) Найти скалярное произведение векторов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
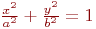
Значения  и
и 
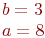
Какая из нижеприведенных точек лежит вне этой кривой.



Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
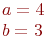 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 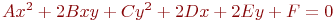 . Найти преобразование координат
. Найти преобразование координат 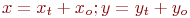 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
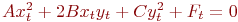 . Указать значение
. Указать значение 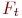 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость ZОХ.
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
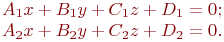 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.Составить уравнение плоскости проходящей через точку с координатами 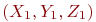 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
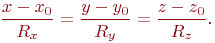
Уравнение представить в виде:
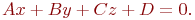
Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
Найти кривизну линии.
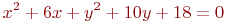 Ответ напишите в виде дроби, например 3/2.
Ответ напишите в виде дроби, например 3/2.Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
a=2; b=-6 a =11,75; b =9,4 a =3,4; b =-4,25 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |
| 0 | 7 | 1 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 6 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 8 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
Заданы координаты двух векторов: (6;9;7) и (3;2;2). Найти сумму векторов.
Найти координаты точки В, симметричной точке А(3;4) относительно оси ОУ.
(-3;4) (2;3) (6;-7) Найти угол между векторами.
Ответ введите с точностью до 1-го знака после запятой.Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
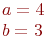 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 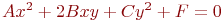 . Найти преобразование координат
. Найти преобразование координат 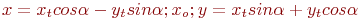 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
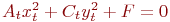 . Указать значение
. Указать значение 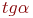 .
.
Найти угол между плоскостью заданной уравнением 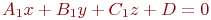 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 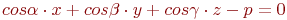
Заданы координаты точки в полярной системе координат: 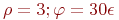 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
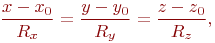
Уравнение прямой представить в виде:
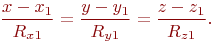
Дан эллиптический параболоид. Определить какие точки ему принадлежат.
Найти радиус линии.
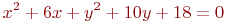
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.
Даны отрезки отсекаемые прямой на осях координат: a=1; b=-2. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 7 | 2 | 2 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 2.5 | 0 | 0 | 42 | 52.5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Дана матрица
Найти обратную матрицу



Заданы координаты двух векторов: (6;9;7) и (3;2;2). Найти разность векторов.
Найти координаты точки В, симметричной точке А(3;4) относительно начала координат.
(-3;-4) (-2;-3) (-6; 7) Найти векторное произведение.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 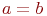 .
.
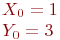
Задано параметрически уравнение эллипса:
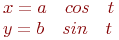
Значения  и
и 
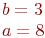
Какая из нижеприведенных точек лежит внутри этой кривой.



Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
Задано уравнение кривой в виде: 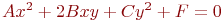 . Найти преобразование координат
. Найти преобразование координат 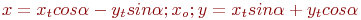 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
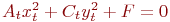 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 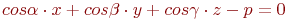 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (3;4). Найти ее координаты в полярной системе координат.




Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через прямую, заданную уравнением:
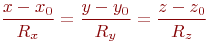
перпендикулярно плоскости:
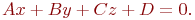
Уравнение представить в виде:
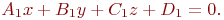
Дан гиперболический параболоид. Определить какие точки ему принадлежат.
Найти координаты центра линии
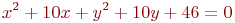
Дана расширенная матрица системы линейных алгебраических уравнений. Найти главный определитель.
Даны отрезки, отсекаемые прямой на осях координат: a=1; b=-2. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
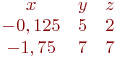
И одно из базисных решений:
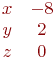
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 15 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их сумму.
Даны координаты трех векторов 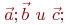 найти коэффициенты в выражении
найти коэффициенты в выражении 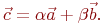
В каком квадранте находится точка А(3,5)
Найти квадрат площади параллелограмма построенного на векторах.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 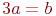 .
.
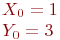
Задано параметрически уравнение эллипса:
Значения  и
и 
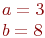
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
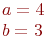 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение кривой в виде: 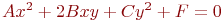 . Найти преобразование координат
. Найти преобразование координат 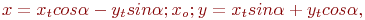 которое приводит уравнение к виду:
которое приводит уравнение к виду:
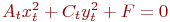 . Указать значение
. Указать значение 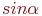 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 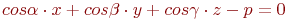 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (4;3;12). Найти ее координаты в цилиндрической системе координат.



Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Укажите проекции направляющего вектора прямой, проходящей через точку 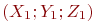 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
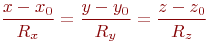
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
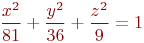
Найти кривизну линии
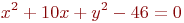
Ответ введите в виде несократимой дроби, например, 3/4.
Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.
Даны отрезки, отсекаемые прямой на осях координат: a=1; b=-2. Найти координаты точки принадлежащей прямой: (5;…).
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
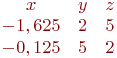
И одно из базисных решений:
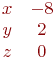
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 0 | 15 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 2 | 3 | 4 | 0 | 0 | 0 | 1 | 64 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их разность.
Даны координаты двух векторов 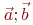 и коэффициенты в выражении
и коэффициенты в выражении 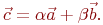
На прямой даны две точки: А(4) и В(8). Найти координаты точки М, которая делит отрезок АВ пополам.
М(6) М(8) М(4) Найти квадрат площади треугольника построенного на векторах.
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 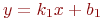 .
.
Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
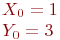
Задано уравнение гиперболы:
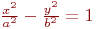
Значения  и
и 
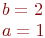
Какая из нижеприведенных точек лежит на этой кривой.
Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
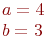
Задано уравнение кривой в виде: Ax2+2Bxy+Cy2+F=0. Найти преобразование координат 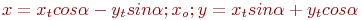 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
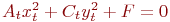 . Указать значение
. Указать значение 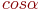 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 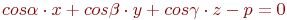 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (8,5;8,5;8,5). Найти ее координаты в сферической системе.



Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
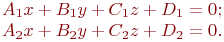
Найти кратчайшее расстояние от точки 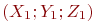 до прямой:
до прямой:
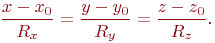 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
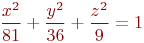
Найти радиус кривизны линии
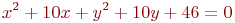
Дана расширенная матрица системы линейных алгебраических уравнений. Найти решение системы.
Через точку с координатами (3;9) проходит прямая, направляющий вектор которой равен (5;4). Найти коэффициенты уравнения этой прямой: y=kx+b.
k=0,8; b=6,6 k=0,25; b=2,5 k=4; b=-1 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
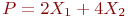
Найти максимальное значение целевой функции.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 2 | 7 | 7 | 1 | 0 | 0 | 0 | 28 | |
| 0 | 6 | 10 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 9 | 7 | 4 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 7 | 2 | 3 | 0 | 0 | 0 | 1 | 64 | |
| 1 | -5 | -8 | -3 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
Даны координаты четырех векторов 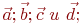 найти коэффициенты в выражении
найти коэффициенты в выражении 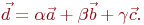
На прямой даны две точки: А(4) и В(10). Найти координаты точки М, лежащей на отрезке AB, если известно, что АМ=2МВ.
М(8) М(9) М(5) Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 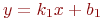 .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
Задано уравнение параболы:
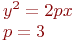
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы  и
и  . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
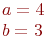



Задано уравнение кривой в виде: 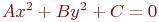 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти угол между плоскостью заданной уравнением 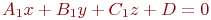 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 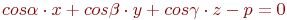 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
Заданы координаты точки в сферической системе координат: 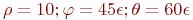 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Найдите кратчайшее расстояние между двумя прямыми:
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
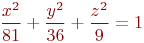
Найти центр тяжести четырех угольника ABCD, если координаты вершин:
Даны координаты вершин треугольника ABC. Найти его площадь.(кв.ед.)
Через точку с координатами (3;9) проходит пряма, направляющий вектор которой равен (5;4). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
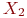 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
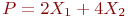
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 5 | 7 | 2 | 0 | 0 | 0 | 1 | 140 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Найти матрицу алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 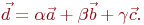 Найти вектор
Найти вектор 
Уравнение эллипса задано параметрически:
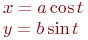
Значения  и
и 
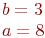
Какая из нижеприведенных точек лежит вне этой кривой?



Найти координату проекции на ось ОХ точки А(7;8).
Найти скалярное произведение векторов.
Заданы координаты точки (6;9) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы два уравнения кривых второго порядка:
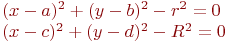
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти тупой угол в градусах между прямой и направлением оси ОХ.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
Задано уравнение эллипса:
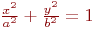
Значения  и
и 
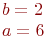
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
Задано уравнение кривой в виде: 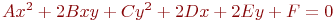 . Найти преобразование координат
. Найти преобразование координат 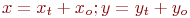 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
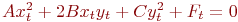 . Указать значение
. Указать значение 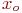 .
.
Найти уравнение плоскости в виде , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
Заданы координаты точки А(7;8;12). Найти координаты ее проекции на координатную плоскость ХОУ.
Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через точку с координатами 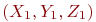 и прямую заданную уравнением:
и прямую заданную уравнением:
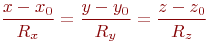
Уравнение представить в виде:
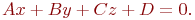
Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
Сколько общих точек имеют линии заданные уравнениями:
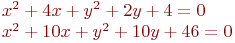
Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 
Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (3;7) и (8;3).
k=2; b=-2 k=-0,8; b=9,4 k=1,25; b=-4,25 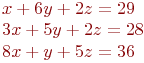
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 3 | 1 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 96 |
| 1 | -4 | -8 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 0 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.

Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
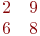
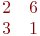
Найти их сумму.



Заданы координаты двух векторов: (2;5) и (2;1). Найти сумму векторов.
Найти координату проекции на ось ОУ точки А(3;8).
Даны два вектора.
Найти угол между ними (в градусах).
(6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
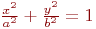
Значения  и
и 
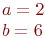
Какая из нижеприведенных точек лежит внутри этой кривой.



Даны полуоси гиперболы 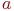 и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
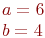 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 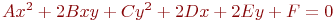 . Найти преобразование координат
. Найти преобразование координат 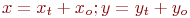 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
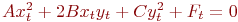 . Указать значение
. Указать значение 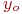 .
.
Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
Заданы координаты точки А(4;3;4). Найти координаты ее проекции на координатную плоскость УОZ.
Найти угол, под которым с плоскостью
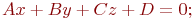
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через прямую уравнением:
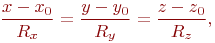
Параллельно прямой:
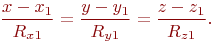
Уравнение представить в виде:
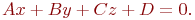
Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
Найти координаты центра линии.
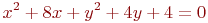
Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
Rx=1; Ry=2 Rx=5; Ry=-4 Rx=4; Ry=5 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И столбец свободных членов:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 6 | 5 | 0 | 1 | 96 |
| 1 | -1 | -7 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их разность.
Заданы координаты двух векторов: (2;5) и (2;1). Найти разность векторов.
Найти координаты точки В, симметричной точке А(2;-3) относительно оси ОХ.
(3;-4) (2;3) (6;-7) Найти скалярное произведение векторов.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
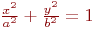
Значения  и
и 
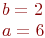
Какая из нижеприведенных точек лежит вне этой кривой.




Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
Задано уравнение кривой в виде: 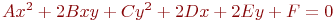 . Найти преобразование координат
. Найти преобразование координат 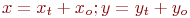 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
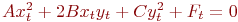 . Указать значение
. Указать значение 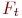 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки А(4;5;3). Найти координаты ее проекции на координатную плоскость ZОХ.
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через точку с координатами 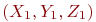 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
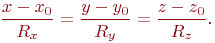
Уравнение представить в виде:
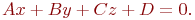
Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
Найти кривизну линии.
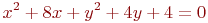 Ответ напишите в виде дроби, например 3/2.
Ответ напишите в виде дроби, например 3/2.Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
a=1; b=-2 a =11,75; b =9,4 a =3,4; b =-4,25 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 1 | 4 | 1 | 0 | 0 | 10 | |
| 0 | 5 | 7 | 1 | 0 | 0 | 1 | 140 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
Заданы координаты двух векторов: (2;5;7) и (2;1;2). Найти сумму векторов.
Найти координаты точки В, симметричной точке А(-2;3) относительно оси ОУ.
(2;3) (-3;4) (6;-7) Найти угол между векторами:
Ответ округлить до целого числа градусов.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
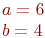 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 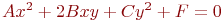 . Найти преобразование координат
. Найти преобразование координат 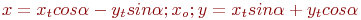 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
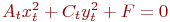 . Указать значение
. Указать значение 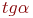 .
.
Найти угол между плоскостью заданной уравнением 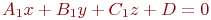 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 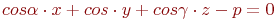
Заданы координаты точки в полярной системе координат: 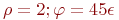 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
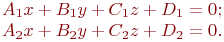
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
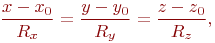
Уравнение прямой представить в виде:
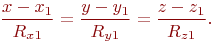
Дан эллиптический параболоид. Определить какие точки ему принадлежат.
Найти радиус линии.
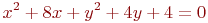
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.
Даны отрезки отсекаемые прямой на осях координат: a=4; b=4. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 10 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 140 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 2,5 | 0 | 0 | 42 | 52,5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Дана матрица
Найти обратную матрицу



Заданы координаты двух векторов: (2;5;7) и (2;1;2). Найти разность векторов.
Найти координаты точки В, симметричной точке А(2;3) относительно начала координат.
(-2;-3) (-3;-4) (-6; 7) Найти векторное произведение.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения с точностью до второго знака после запятой.
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 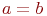 .
.
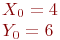
Задано параметрически уравнение эллипса:
Значения  и
и 
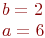
Какая из нижеприведенных точек лежит внутри этой кривой.



Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
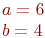 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 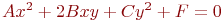 . Найти преобразование координат
. Найти преобразование координат 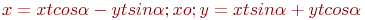 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
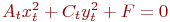 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 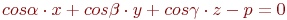 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (6;8). Найти ее координаты в полярной системе координат. Укажите угол с точностью до одного знака после запятой.



Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
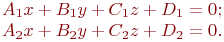 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.Составить уравнение плоскости проходящей через прямую, заданную уравнением:
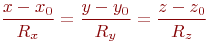
перпендикулярно плоскости:
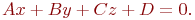
Уравнение представить в виде:
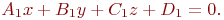
Дан гиперболический параболоид. Определить какие точки ему принадлежат.
Найти координаты центра линии
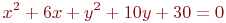
Дана расширенная матрица системы линейных алгебраических уравнений. Найти главный определитель.
Даны отрезки, отсекаемые прямой на осях координат: a=4; b=4. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
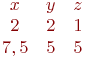
И одно из базисных решений:
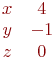
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 25 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 280 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их сумму.
Даны координаты трех векторов 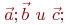 найти коэффициенты в выражении
найти коэффициенты в выражении 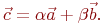
В каком квадранте находится точка А(-3,5)
Найти квадрат площади параллелограмма построенного на векторах:
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат. Ответ введите с точностью до 2-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 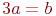 .
.
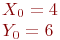
Задано параметрически уравнение эллипса:
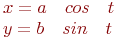
Значения  и
и 
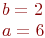
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
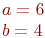 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 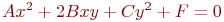 . Найти преобразование координат
. Найти преобразование координат 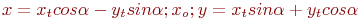 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
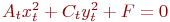 . Указать значение
. Указать значение 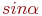 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 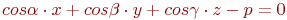 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (6;8;12). Найти ее координаты в цилиндрической системе координат.




Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Укажите проекции направляющего вектора прямой, проходящей через точку 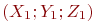 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
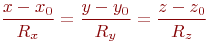
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
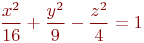
Найти кривизну линии
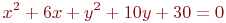 Ответ укажите с точностью до одного знака после запятой.
Ответ укажите с точностью до одного знака после запятой.Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.
Даны отрезки, отсекаемые прямой на осях координат: a=4; b=4. Найти координаты точки принадлежащей прямой: (5;…).
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
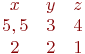
И одно из базисных решений:
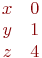
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 0 | 25 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 0 | 280 | |
| 0 | 12 | 6 | 7 | 0 | 0 | 0 | 1 | 54 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их разность.
Даны координаты трех векторов 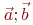 и коэффициенты в выражении
и коэффициенты в выражении 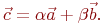 Найти вектор
Найти вектор 
На прямой даны две точки: А(2) и В(14). Найти координаты точки М, которая делит отрезок АВ пополам.
М(8) М(6) М(4) Найти квадрат площади треугольника, построенного на векторах:
Ответ введите с точностью до 1-го знака после запятой.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a=5; вдоль оси ОУ на b=4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 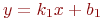 .
.
Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
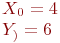
Задано уравнение гиперболы:
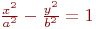
Значения  и
и 
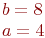
Какая из нижеприведенных точек лежит на этой кривой.





Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
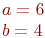
Задано уравнение кривой в виде: 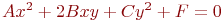 . Найти преобразование координат
. Найти преобразование координат 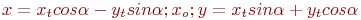 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
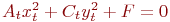 . Указать значение
. Указать значение 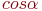 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 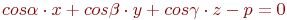 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (3;2;5). Найти ее координаты в сферической системе.



Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Найти кратчайшее расстояние от точки 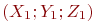 до прямой:
до прямой:
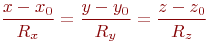 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
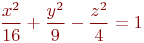
Найти радиус кривизны линии
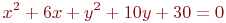
Дана расширенная матрица системы линейных алгебраических уравнений. Найти решение системы.
Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти коэффициенты уравнения этой прямой: y=kx+b.
k=0,8; b=6,6 k=0,25; b=2,5 k=4; b=-1 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
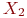 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
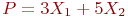 Найти максимум.
Найти максимум.Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 1 | 6 | 5 | 1 | 0 | 0 | 0 | 24 | |
| 0 | 2 | 7 | 3 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 3 | 6 | 2 | 0 | 0 | 1 | 0 | 280 | |
| 0 | 5 | 3 | 4 | 0 | 0 | 0 | 1 | 54 | |
| 1 | -4 | -7 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
Даны координаты четырех векторов 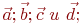 найти коэффициенты в выражении
найти коэффициенты в выражении 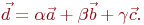
На прямой даны две точки: А(3) и В(12). Найти координату точки М, если известно, что 2АМ=МВ.
6 8 5 4 7 Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 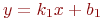 .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
Задано уравнение параболы:
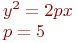
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы  и
и  . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
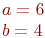



Задано уравнение кривой в виде: 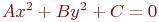 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти острый угол между плоскостью заданной уравнением 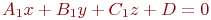 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 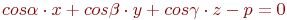 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
Заданы координаты точки в сферической системе координат: 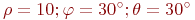 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
 ;
; ;
; )
)  ;
; ;
; )
)  ;
; ;
; )
)  ;
; ;
; )
) Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Найдите кратчайшее расстояние между двумя прямыми:
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
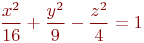
Найти центр тяжести четырех угольника ABCD, если координаты вершин:
Даны координаты вершин треугольника ABC. Найти его площадь. (кв.ед.)
Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
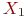 | 20 | 0 | 0 | 10 |
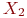 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
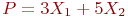
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 6 | 6 | 8 | 1 | 0 | 0 | 0 | 24 | |
| 0 | 5 | 3 | 6 | 0 | 1 | 0 | 0 | 70 | |
| 0 | 6 | 2 | 5 | 0 | 0 | 1 | 0 | 150 | |
| 0 | 8 | 9 | 2 | 0 | 0 | 0 | 1 | 52 | |
| 1 | -3 | -4 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Найти матрицу алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 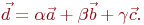 Найти вектор
Найти вектор 
Задано параметрически уравнение эллипса:
Значения  и
и 
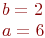
Какая из нижеприведенных точек лежит вне этой кривой.



Найти координату проекции на ось ОХ точки А(9;2).
Найти скалярное произведение векторов.
Заданы координаты точки (8;7) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
Задано уравнение эллипса:
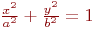
Значения  и
и 
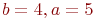
Какая из нижеприведенных точек лежит на этой кривой.





Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
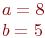 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 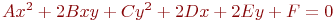 . Найти преобразование координат
. Найти преобразование координат 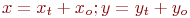 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
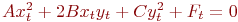 . Указать значение
. Указать значение 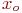 .
.
Найти уравнение плоскости в виде  , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
Заданы координаты точки А(2;4;7). Найти координаты ее проекции на координатную плоскость ХОУ.
Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
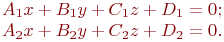
Составить уравнение плоскости проходящей через точку с координатами 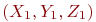 и прямую заданную уравнением:
и прямую заданную уравнением:
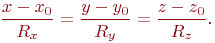
Уравнение представить в виде:
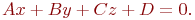
Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
Сколько общих точек имеют линии заданные уравнениями:
Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 
Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (5;2) и (9;7).
k=2; b=-2 k=-0,8; b=9,4 k=1,25; b=-4,25 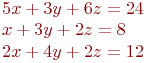
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 5 |
| 0 | 2 | 9 | 0 | 1 | 45 |
| 1 | -4 | -5 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 1 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
Найти их сумму.
Заданы координаты двух векторов: (1;9) и (5;2). Найти сумму векторов.
Найти координату проекции на ось ОУ точки А(4;2).
Даны два вектора.
Найти угол между ними (в градусах).
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
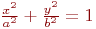
Значения  и
и 
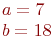
Какая из нижеприведенных точек лежит внутри этой кривой.




Даны полуоси гиперболы.  и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
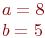 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 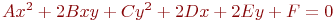 . Найти преобразование координат
. Найти преобразование координат 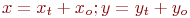 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
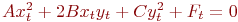 . Указать значение
. Указать значение 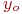 .
.
Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
Заданы координаты точки А(7;5;8). Найти координаты ее проекции на координатную плоскость УОZ.
Найти угол, под которым с плоскостью
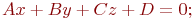
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через прямую уравнением:
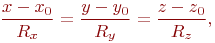
Параллельно прямой:
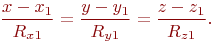
Уравнение представить в виде:
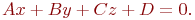
Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
Найти координаты центра линии.
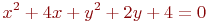
Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
Rx=1; Ry=2 Rx=5; Ry=-4 Rx=4; Ry=5 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И столбец свободных членов:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 3 | 1 | 1 | 0 | 5 |
| 0 | 6 | 5 | 0 | 1 | 45 |
| 1 | -3 | -7 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их разность.
Заданы координаты двух векторов: (1;9) и (5;2). Найти разность векторов.
Найти координаты точки В, симметричной точке А(6;7) относительно оси ОХ.
(6;-7) (3;-4) (2;3) Найти скалярное произведение векторов.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
Задано уравнение эллипса:
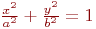
Значения  и
и 
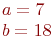
Какая из нижеприведенных точек лежит внутри этой кривой.



Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
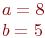 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Условия.
Задано уравнение кривой в виде: 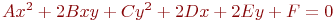 . Найти преобразование координат
. Найти преобразование координат 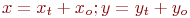 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
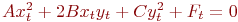 . Указать значение
. Указать значение 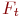 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки А(8;5;5). Найти координаты ее проекции на координатную плоскость ZОХ.
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
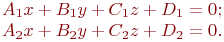 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.Составить уравнение плоскости проходящей через точку с координатами 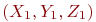 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
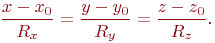
Уравнение представить в виде:
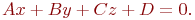
Дан двуполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
Найти кривизну линии.
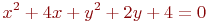
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
a=1; b=-2 a =11,75; b =9,4 a =3,4; b =-4,25 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 1 | 3 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 4,5 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 8 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
Заданы координаты двух векторов: (1;9;7) и (5;2;2). Найти сумму векторов.
Найти координаты точки В, симметричной точке А(-6;-7) относительно оси ОУ.
(6;-7) (-3;4) (2;3) Найти угол между векторами.
Ответ введите с округлением до целого.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми. Ответ округлить до второй цифры после запятой.
Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
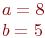 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 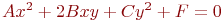 . Найти преобразование координат
. Найти преобразование координат 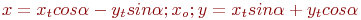 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
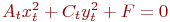 . Указать значение
. Указать значение 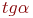 .
.
Найти острый угол между плоскостью заданной уравнением 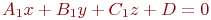 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 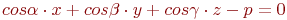


Заданы координаты точки в полярной системе координат: 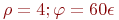 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
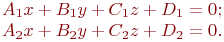
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
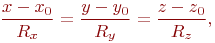
Уравнение прямой представить в виде:
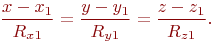
 . Найдите значение
. Найдите значение  в точке с координатами:
в точке с координатами:  .
.Найти радиус линии.
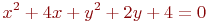
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.
Даны отрезки отсекаемые прямой на осях координат: a=2; b=7. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
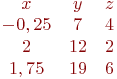
И одно из базисных решений:
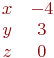
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 5 | 3 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 2.5 | 0 | 0 | 42 | 52.5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Дана матрица
Найти обратную матрицу



Заданы координаты двух векторов: (1;9;7) и (5;2;2). Найти разность векторов.
Найти координаты точки В, симметричной точке А(6;-7) относительно начала координат.
(-6; 7) (-3;-4) (-2;-3) Найти векторное произведение.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 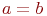 .
.
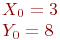
Задано параметрически уравнение эллипса:
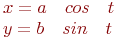
Значения  и
и 
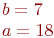
Какая из нижеприведенных точек лежит внутри этой кривой.




Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
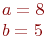 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 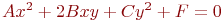 . Найти преобразование координат
. Найти преобразование координат 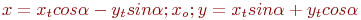 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
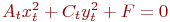 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 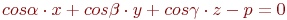 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
(8;6). Найти ее координаты в полярной системе координат. В качестве ответа введите угол, округлив его до целого.Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Составить уравнение плоскости проходящей через прямую, заданную уравнением:
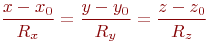
перпендикулярно плоскости:
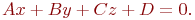
Уравнение представить в виде:

Дан гиперболический параболоид. Определить какие точки ему принадлежат.
Найти координаты центра линии
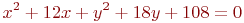
Дана расширенная матрица системы линейных алгебраических уравнений. Найти главный определитель.
Даны отрезки, отсекаемые прямой на осях координат: a=2; b=7. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
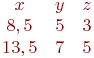
И одно из базисных решений:
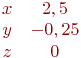
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их сумму.
Даны координаты трех векторов 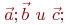 найти коэффициенты в выражении
найти коэффициенты в выражении 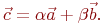
В каком квадранте находится точка А(3,-5)
Найти квадрат площади параллелограмма, построенного на векторах:
После трансляции координаты точки приняли значение (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 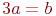 .
.
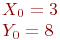
Задано параметрически уравнение эллипса:
Значения  и
и 
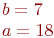
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
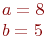 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение кривой в виде: 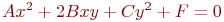 . Найти преобразование координат
. Найти преобразование координат 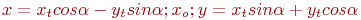 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
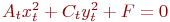 . Указать значение
. Указать значение 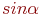 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 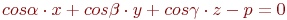 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (8;6;12). Найти ее координаты в цилиндрической системе координат.



Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
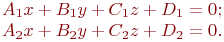
Укажите проекции направляющего вектора прямой, проходящей через точку 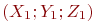 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
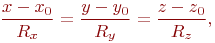
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
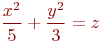
Найти кривизну линии
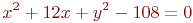
Ответ представьте в виде несократимой дроби.
Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.
Даны отрезки, отсекаемые прямой на осях координат: a=2; b=7. Найти координаты точки принадлежащей прямой: (5;…).
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
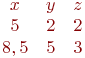
И одно из базисных решений:
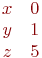
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 5 | 7 | 2 | 0 | 0 | 0 | 1 | 140 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их разность.
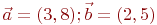 . Найти координаты вектора
. Найти координаты вектора 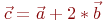 .
.




На прямой даны две точки: А(1) и В(7). Найти координаты точки М, которая делит отрезок АВ пополам.
М(4) М(6) М(8) После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 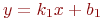 .
.
Угол (в градусах) между прямыми.
Ответ введите с точностью до 1-го знака после запятой.Найти отрезки, отсекаемые на осях координат (b на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
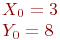
Задано уравнение гиперболы:
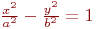
Значения  и
и 
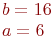
Какая из нижеприведенных точек лежит на этой кривой.




Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
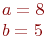
Задано уравнение кривой в виде: 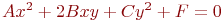 . Найти преобразование координат
. Найти преобразование координат 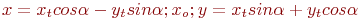 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
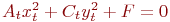 . Указать значение
. Указать значение 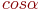 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 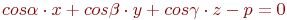 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
Заданы координаты точки в декартовой системе координат (7;4;2). Найти ее координаты в сферической системе.



Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Найти кратчайшее расстояние от точки  до прямой:
до прямой:
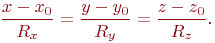 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
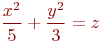
Найти радиус кривизны линии
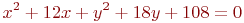
Дана расширенная матрица системы линейных алгебраических уравнений. Найти решение системы.
(3;12) проходит пряма, направляющий вектор которой равен (2;7). Найти коэффициенты уравнения этой прямой: y=kx+b.k=0,25; b=6,5 k=0,25; b=2,5 k=3,5; b=1,5 k=3,5; b=0,25 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
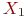 | 20 | 0 | 0 | 10 |
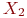 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
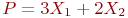
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 5 | 3 | 9 | 1 | 0 | 0 | 0 | 6 | |
| 0 | 2 | 3 | 7 | 0 | 1 | 0 | 0 | 8 | |
| 0 | 3 | 4 | 5 | 0 | 0 | 1 | 0 | 9 | |
| 0 | 4 | 6 | 3 | 0 | 0 | 0 | 1 | 13 | |
| 1 | -4 | -5 | -1 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
Даны координаты четырех векторов 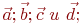 найти коэффициенты в выражении
найти коэффициенты в выражении 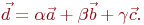
На прямой даны две точки: А(1) и В(7). Найти координаты точки М, если известно, что АМ=2МВ.
М(8) М(9) М(5) Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде 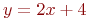 и
и 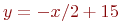 . Найдите угол (в градусах) между прямыми.
. Найдите угол (в градусах) между прямыми.
Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
Задано уравнение параболы:
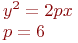
Какая из нижеприведенных точек лежит на этой кривой.



Даны полуоси гиперболы 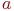 и
и 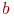 . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
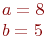



Задано уравнение кривой в виде: 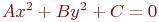 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти угол между плоскостью заданной уравнением 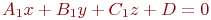 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 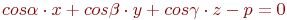 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
Заданы координаты точки в сферической системе координат: 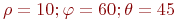 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
Найдите кратчайшее расстояние между двумя прямыми:
Ответ введите с точностью до 2-го знака после запятой.Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью эаданной уравнением:
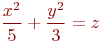
Найти центр тяжести четырех угольника ABCD, если координаты вершин:
Даны координаты вершин треугольника ABC. Найти его площадь. (кв.ед.)
Через точку с координатами (3;11) проходит прямая, направляющий вектор которой равен (1;4). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
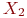 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
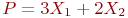
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 0 | 12 | |
| 0 | 8 | 9 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 4 | 6 | 2 | 0 | 0 | 1 | 0 | 80 | |
| 0 | 7 | 4 | 7 | 0 | 0 | 0 | 1 | 32 | |
| 1 | -1 | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Найти матрицу алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 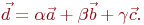 Найти вектор
Найти вектор 
Задано параметрически уравнение эллипса:
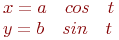
Значения  и
и 
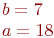
Какая из нижеприведенных точек лежит внутри этой кривой.


