Главная /
Математика /
Дискретный анализ и теория вероятностей
Дискретный анализ и теория вероятностей - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: В рамках курса рассматриваются основные понятия и методы комбинаторного, дискретного и асимптотического анализа, теории вероятностей, статистики и на примере решения классических задач демонстрируется их применение.
Все ответы: В рамках курса рассматриваются основные понятия и методы комбинаторного, дискретного и асимптотического анализа, теории вероятностей, статистики и на примере решения классических задач демонстрируется их применение.
Смотрите также:
Как называется упорядоченный набор из ![math]() различных элементов некоторого
различных элементов некоторого ![math]() -элементного множества?
-элементного множества?
 различных элементов некоторого
различных элементов некоторого  -элементного множества?
-элементного множества?
(1) размещением из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(2) размещением из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(3) сочетанием из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(4) сочетанием из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
Случайная величина ![math]() принимает только 4 значения:
принимает только 4 значения: ![math]() .Известно, что
.Известно, что ![math]() ,
, ![math]() ,
, ![math]() . Чему равна
. Чему равна ![math]() ?
?
 принимает только 4 значения:
принимает только 4 значения:  .Известно, что
.Известно, что  ,
,  ,
,  . Чему равна
. Чему равна  ?
?
0,2
Запишите окончание формулировки неравенства Маркова. Пусть ![math]() и пусть
и пусть ![math]() . Тогда...
. Тогда...
 и пусть
и пусть  . Тогда...
. Тогда...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() - выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин
- выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин ![math]() . Пусть
. Пусть ![math]() - эмпирическая функция распределения. Какое утверждение относительно ее является верным?
- эмпирическая функция распределения. Какое утверждение относительно ее является верным?
 - выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин
- выборка. Предполжим, что выборка является реализацией некоторых одинаково распределенных, независимых случайных величин  . Пусть
. Пусть  - эмпирическая функция распределения. Какое утверждение относительно ее является верным?
- эмпирическая функция распределения. Какое утверждение относительно ее является верным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть имеется некоторое множество ![math]() . На
. На ![math]() - множестве всех возможных подмножеств определено ЧУМ. Определите критерий для
- множестве всех возможных подмножеств определено ЧУМ. Определите критерий для ![math]() .
.
 . На
. На  - множестве всех возможных подмножеств определено ЧУМ. Определите критерий для
- множестве всех возможных подмножеств определено ЧУМ. Определите критерий для  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Что допускается в простом графе?
(1) кратные ребра
(2) ничего из перечисленного
(3) петли
(4) ориентация ребер
Если раскрыть скобки в бесконечном произведении ![math]() , чему равен коэффициент при
, чему равен коэффициент при ![math]() ?
?
 , чему равен коэффициент при
, чему равен коэффициент при  ?
?
0
Говорят, что степенной ряд ![math]() сходится в точке
сходится в точке ![math]() , если сходятся его частичные суммы
, если сходятся его частичные суммы ![math]() .Это утверждение является...
.Это утверждение является...
 сходится в точке
сходится в точке  , если сходятся его частичные суммы
, если сходятся его частичные суммы  .Это утверждение является...
.Это утверждение является...
(1) определением сходимости
(2) необходимым условием сходимости
(3) достаточным условием сходимости
(4) критерием сходимости
Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер. Подмножество
– множество ребер. Подмножество ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() не принадлежит
не принадлежит ![math]() .
.
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер. Подмножество
– множество ребер. Подмножество  называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  не принадлежит
не принадлежит  .
.
(1) клика
(2) независимое множество
(3) зависимое множество
(4) хроматическое множество
Выберите все утверждения верные согласно классическому определению вероятности относительно конечного множества элементарных исходов.
(1) множество элементарных исходов содержит все возможные исходы
(2) исходы попарно несовместны
(3) исходы взаимно независимы
(4) исходы равновозможны
Что согласно локальной леммы Ловаса является верным для событий, определенныx следующим образом? Пусть ![math]() события, для каждого из которых выполнено
события, для каждого из которых выполнено ![math]() и любое событие
и любое событие ![math]() независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем ![math]() штук, причем и
штук, причем и ![math]() .Тогда ...
.Тогда ...
 события, для каждого из которых выполнено
события, для каждого из которых выполнено  и любое событие
и любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук, причем и
штук, причем и  .Тогда ...
.Тогда ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

Имеются два множества непересекающихся объектов: множество ![math]() и множество
и множество ![math]() .Количество способов выбрать либо один объект из множества
.Количество способов выбрать либо один объект из множества ![math]() либо один объект из множества
либо один объект из множества ![math]() определяется ...
определяется ...
 и множество
и множество  .Количество способов выбрать либо один объект из множества
.Количество способов выбрать либо один объект из множества  либо один объект из множества
либо один объект из множества  определяется ...
определяется ...
(1) по правилу умножения и равно ![math]()

(2) по правилу сложения и равно ![math]()

(3) по правилу умножения и равно ![math]()

(4) по правилу сложения и равно ![math]()

(5) по принципу Дирихле и равно ![math]()

(6) по принципу Дирихле и равно ![math]()

Выберите дискретные распределения из перечисленных.
(1) нормальное распределение
(2) распределение Бернулли
(3) распределение Вейбулла
(4) распределение Пуассона
Пусть ![math]() - случайный граф, множество, состоящее из
- случайный граф, множество, состоящее из ![math]() вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью ![math]() , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от ![math]() . Если
. Если ![math]() , то к чему ассимптотически стремиться вероятность того, что в случайном графе нет треугольников?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе нет треугольников?
 - случайный граф, множество, состоящее из
- случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Если
. Если  , то к чему ассимптотически стремиться вероятность того, что в случайном графе нет треугольников?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе нет треугольников?
1
Пусть ![math]() последовательность независимых событий:
последовательность независимых событий: ![math]() . Положим
. Положим ![math]() . Тогда к какой величине при
. Тогда к какой величине при ![math]() сходится
сходится ![math]() почти наверное?
почти наверное?
 последовательность независимых событий:
последовательность независимых событий:  . Положим
. Положим  . Тогда к какой величине при
. Тогда к какой величине при  сходится
сходится  почти наверное?
почти наверное?
0
Согласно обобщенной формуле обращения Мебиуса ![math]() тогда, когда...
тогда, когда...
 тогда, когда...
тогда, когда...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В теории графов дерево это - ...
(1) связанный ациклический граф
(2) связанный циклический граф
(3) несвязанный ациклический граф
(4) несвязанный унициклический граф
Сколько существует разложений натурального числа 10 в виде упорядоченной суммы натуральных слагаемых?
512
Если говорить о ![math]() и
и ![math]() как о формальных степенных рядах, какие из перечисленных утверждений являются верными?
как о формальных степенных рядах, какие из перечисленных утверждений являются верными?
 и
и  как о формальных степенных рядах, какие из перечисленных утверждений являются верными?
как о формальных степенных рядах, какие из перечисленных утверждений являются верными?
(1) радиус сходимости равен 0
(2) радиус сходимости равен 1
(3) ряды различаются
(4) ряды совпадают
(5) при ![math]() равны 1
равны 1
 равны 1
равны 1 Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.Число независимости графа -
– множество ребер.Число независимости графа -
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.Число независимости графа -
– множество ребер.Число независимости графа -
(1) минимальное число цветов, в которые можно покрасить вершины, так чтобы любые две вершины, соединенные ребром были покрашены в разные цвета
(2) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() принадлежит
принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  принадлежит
принадлежит 
(3) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() не принадлежит
не принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  не принадлежит
не принадлежит 
Определите все элементарные исходы,котороые при бросании монеты образуют событие, что выпало простое число очков.
(1) выпало 1 очко
(2) выпало 2 очка
(3) выпало 3 очка
(4) выпало 4 очка
(5) выпало 5 очков
(6) выпало 6 очков
Пусть ![math]() события. Формулировка "любое событие
события. Формулировка "любое событие ![math]() независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем ![math]() штук" означает, что ...
штук" означает, что ...
 события. Формулировка "любое событие
события. Формулировка "любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук" означает, что ...
штук" означает, что ...
(1) из множества ![math]() найдется подмножество
найдется подмножество ![math]() , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых ![math]() не зависит
не зависит
 найдется подмножество
найдется подмножество  , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
(2) из множества ![math]() найдется подмножество
найдется подмножество ![math]() , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых ![math]() не зависит
не зависит
 найдется подмножество
найдется подмножество  , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
(3) из множества ![math]() найдется подмножество
найдется подмножество ![math]() , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых ![math]() не зависит
не зависит
 найдется подмножество
найдется подмножество  , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит
(4) из множества ![math]() найдется подмножество
найдется подмножество ![math]() , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых ![math]() не зависит
не зависит
 найдется подмножество
найдется подмножество  , состоящее из событий, от совокупности которых
, состоящее из событий, от совокупности которых  не зависит
не зависит Какая формула определяет количество сочетаний из ![math]() элементов по
элементов по ![math]() без повторений?
без повторений?
 элементов по
элементов по  без повторений?
без повторений?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Что означает запись ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть случайная величина ![math]() , математическое ожидание квадрата данной случайной величины конечно
, математическое ожидание квадрата данной случайной величины конечно ![math]() и имеется
и имеется ![math]() . Какое утверждение, согласно неравенству Чебышева, является верным?
. Какое утверждение, согласно неравенству Чебышева, является верным?
 , математическое ожидание квадрата данной случайной величины конечно
, математическое ожидание квадрата данной случайной величины конечно  и имеется
и имеется  . Какое утверждение, согласно неравенству Чебышева, является верным?
. Какое утверждение, согласно неравенству Чебышева, является верным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим пару ![math]() , где
, где ![math]() - любое множество,
- любое множество, ![math]() - совокупность подмножеств в
- совокупность подмножеств в ![math]() . Пусть
. Пусть ![math]() конечное множество, а любое
конечное множество, а любое ![math]() имеет мощность равную 2, что в таком случае представляет собой пара
имеет мощность равную 2, что в таком случае представляет собой пара ![math]() ?
?
 , где
, где  - любое множество,
- любое множество,  - совокупность подмножеств в
- совокупность подмножеств в  . Пусть
. Пусть  конечное множество, а любое
конечное множество, а любое  имеет мощность равную 2, что в таком случае представляет собой пара
имеет мощность равную 2, что в таком случае представляет собой пара  ?
?
(1) однородный гиперграф
(2) граф
(3) ранжированное пространство
(4) топологическое пространство
Пусть задано частично упорядоченное множество (ЧУМ) ![math]() , и для каждого элемента
, и для каждого элемента ![math]() найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса ![math]() на ЧУМ
на ЧУМ ![math]() , если
, если ![math]() ?
?
 , и для каждого элемента
, и для каждого элемента  найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса  на ЧУМ
на ЧУМ  , если
, если  ?
?
1
Чему равно ![math]() - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на ![math]() вершинах?
вершинах?
 - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на  вершинах?
вершинах?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколько существует разложений натурального числа 10 в виде упорядоченной суммы натуральных слагаемых длины ровно 4?
42
Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.
– множество ребер.![math]() число независимости и
число независимости и ![math]() кликовое число. Какое утверждение является верным?
кликовое число. Какое утверждение является верным?
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. число независимости и
число независимости и 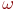 кликовое число. Какое утверждение является верным?
кликовое число. Какое утверждение является верным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Числом Рамсея ![math]() называется минимальное число
называется минимальное число ![math]() такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа ![math]() в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф ![math]() , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф ![math]() , у которого все ребра синие. Чему равно
, у которого все ребра синие. Чему равно ![math]() ?
?
 называется минимальное число
называется минимальное число  такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа  в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф  , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф  , у которого все ребра синие. Чему равно
, у которого все ребра синие. Чему равно  ?
?
1
Рассмотрим 30 шестиэлементных множеств ![math]() , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие ![math]() означает, что
означает, что ![math]() множество одноцветно. Чему равна вероятность выбрать опреденную раскраску?
множество одноцветно. Чему равна вероятность выбрать опреденную раскраску?
 , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие  означает, что
означает, что  множество одноцветно. Чему равна вероятность выбрать опреденную раскраску?
множество одноцветно. Чему равна вероятность выбрать опреденную раскраску?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равен биномиальный коэффициент перед выражением ![math]() при разложении
при разложении ![math]() ?
?
 при разложении
при разложении  ?
?
10
Что означает запись ![math]() ?
?
 ?
?
(1)
(2)
(3)
(4) ![math]()

Как формулируется закон больших чисел (в форме Чебышева)? Пусть ![math]() последовательность одинаково распределенных независимых в совокупности, у которых математические ожидания случайных величин и их квадратов конечны
последовательность одинаково распределенных независимых в совокупности, у которых математические ожидания случайных величин и их квадратов конечны ![math]() . Тогда
. Тогда ![math]() при
при ![math]() ...
...
 последовательность одинаково распределенных независимых в совокупности, у которых математические ожидания случайных величин и их квадратов конечны
последовательность одинаково распределенных независимых в совокупности, у которых математические ожидания случайных величин и их квадратов конечны  . Тогда
. Тогда  при
при  ...
...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим ![math]() . Назовем проекцией
. Назовем проекцией ![math]() на
на ![math]()
![math]() .
. ![math]() дробится (split up) с помощью
дробится (split up) с помощью ![math]() , если
, если ![math]() . Что из перечисленного является определением размерности Вапника-Червоненкиса?
. Что из перечисленного является определением размерности Вапника-Червоненкиса?
 . Назовем проекцией
. Назовем проекцией  на
на 
 .
.  дробится (split up) с помощью
дробится (split up) с помощью  , если
, если  . Что из перечисленного является определением размерности Вапника-Червоненкиса?
. Что из перечисленного является определением размерности Вапника-Червоненкиса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть отношение «… делитель…» определяет частичный порядок на множестве ![math]() . Чему равно значение элемента, который является непосредственным предшественником элемента, равного 18?
. Чему равно значение элемента, который является непосредственным предшественником элемента, равного 18?
 . Чему равно значение элемента, который является непосредственным предшественником элемента, равного 18?
. Чему равно значение элемента, который является непосредственным предшественником элемента, равного 18?
6
На рисунке представлено дерево. Укажите вершину, которую согласно алгоритму в коде Прюфера, следует удалить в первую очередь.
![files]()

2
Сколько существует диаграмм Юнга произвольного веса, но имеющих не более 7 строк и 3 столбцов?
119
Чему равен десятый член последовательности, если![math]() ?
?
 ?
?
55
Пусть имеется простой граф ![math]() ,построенный на
,построенный на ![math]() вершинах. Какое утверждение относительно
вершинах. Какое утверждение относительно ![math]() кликового числа графа является верным при больших
кликового числа графа является верным при больших ![math]() ?
?
 ,построенный на
,построенный на  вершинах. Какое утверждение относительно
вершинах. Какое утверждение относительно  кликового числа графа является верным при больших
кликового числа графа является верным при больших  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Числом Рамсея ![math]() называется минимальное число
называется минимальное число ![math]() такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа ![math]() в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф ![math]() , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф ![math]() , у которого все ребра синие. Чему равен порядок
, у которого все ребра синие. Чему равен порядок ![math]() ?
?
 называется минимальное число
называется минимальное число  такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа  в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф  , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф  , у которого все ребра синие. Чему равен порядок
, у которого все ребра синие. Чему равен порядок  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Не меньше какого числа должно быть ![math]() , чтобы выполнялось следующая теорема? Пусть
, чтобы выполнялось следующая теорема? Пусть ![math]()
![math]() -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем ![math]() множествам
множествам ![math]() , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного ![math]() -элементного подмножества.
-элементного подмножества.
 , чтобы выполнялось следующая теорема? Пусть
, чтобы выполнялось следующая теорема? Пусть 
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем  множествам
множествам  , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного  -элементного подмножества.
-элементного подмножества.
9
Сколькими способами можно переставить буквы в слове «МОЛОКО» так, чтобы получилось новое слово (возможно бессмысленное)?
120
Выберите свойства функции распределения.
(1) монотонно неубывет
(2) монотонно возрастает
(3) непрерывна справа
(4) непрерывна слева
Пусть случайные величины ![math]() , определенные на некотором
, определенные на некотором ![math]() , если для любого
, если для любого ![math]() при
при ![math]() выполняется условие
выполняется условие ![math]() , то говорят, что
, то говорят, что ![math]() сходится к
сходится к ![math]() ...
...
 , определенные на некотором
, определенные на некотором  , если для любого
, если для любого  при
при  выполняется условие
выполняется условие  , то говорят, что
, то говорят, что  сходится к
сходится к  ...
...
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Имеется ранжированное пространство ![math]() , есть некоторое конечное подмножество
, есть некоторое конечное подмножество ![math]() из
из ![math]()
![math]() . и есть число
. и есть число ![math]() . Назовем
. Назовем ![math]()
![math]() -сетью для
-сетью для ![math]() , если
, если ![math]() для любого
для любого ![math]() ...
...
 , есть некоторое конечное подмножество
, есть некоторое конечное подмножество  из
из 
 . и есть число
. и есть число  . Назовем
. Назовем 
 -сетью для
-сетью для  , если
, если  для любого
для любого  ...
...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Журнал А читают 70% студентов, журнал В – 40% студентов, журнал С – 50% студентов; 30% студентов читают журналы А и В, 40% - журналы А и С, 20% - журналы В и С, 10% - журналы А, В и С. Сколько процентов студентов читают хотя бы один журнал?
80
Сколько ребер у связного унициклического графа с 5 вершинами?
5
Какой знак можно поставить между числом неупорядоченных разбиений числа ![math]() на не более чем
на не более чем ![math]() слагаемых и числом неупорядоченных разбиений числа
слагаемых и числом неупорядоченных разбиений числа ![math]() на
на ![math]() слагаемых?
слагаемых?
 на не более чем
на не более чем  слагаемых и числом неупорядоченных разбиений числа
слагаемых и числом неупорядоченных разбиений числа  на
на  слагаемых?
слагаемых?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равен третий член последовательности числе Фибоначчи?
2
Как называется граф ![math]() построенный следующим образом? Имеется
построенный следующим образом? Имеется ![math]() - множество натуральных чисел от 1 до
- множество натуральных чисел от 1 до ![math]() . Множество вершин данного графа образуют все
. Множество вершин данного графа образуют все ![math]() -элементные подмножества из множества
-элементные подмножества из множества ![math]() . Говорят, что пара
. Говорят, что пара ![math]() образуют ребро графа, тогда и только тогда
образуют ребро графа, тогда и только тогда ![math]() .
.
 построенный следующим образом? Имеется
построенный следующим образом? Имеется  - множество натуральных чисел от 1 до
- множество натуральных чисел от 1 до  . Множество вершин данного графа образуют все
. Множество вершин данного графа образуют все  -элементные подмножества из множества
-элементные подмножества из множества  . Говорят, что пара
. Говорят, что пара  образуют ребро графа, тогда и только тогда
образуют ребро графа, тогда и только тогда  .
.
(1) граф Петерсена
(2) Кнезероский граф
(3) граф Эйлера
(4) граф Мура
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Чему равна вероятность при случайном выборе выбрать одну определенную раскраску?
в два цвета - красный и синий. Чему равна вероятность при случайном выборе выбрать одну определенную раскраску?
 в два цвета - красный и синий. Чему равна вероятность при случайном выборе выбрать одну определенную раскраску?
в два цвета - красный и синий. Чему равна вероятность при случайном выборе выбрать одну определенную раскраску?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Орграф зависимостей для ![math]() - это произвольный орграф
- это произвольный орграф ![math]() удовлетворяющий условиям... Выберите все условия.
удовлетворяющий условиям... Выберите все условия.
 - это произвольный орграф
- это произвольный орграф  удовлетворяющий условиям... Выберите все условия.
удовлетворяющий условиям... Выберите все условия.
(1) ![math]() - вершины орграфа
- вершины орграфа
 - вершины орграфа
- вершины орграфа
(2) ![math]() не зависит от совокупности всех
не зависит от совокупности всех ![math]() таких, что
таких, что ![math]()
 не зависит от совокупности всех
не зависит от совокупности всех  таких, что
таких, что 
(3) ![math]() зависит от совокупности всех
зависит от совокупности всех ![math]() таких, что
таких, что ![math]()
 зависит от совокупности всех
зависит от совокупности всех  таких, что
таких, что 
(4) ![math]() не зависит от совокупности всех
не зависит от совокупности всех ![math]() таких, что
таких, что ![math]()
 не зависит от совокупности всех
не зависит от совокупности всех  таких, что
таких, что 
Выберите все выражения равные ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Случайная величина ![math]() принимает только 4 значения:
принимает только 4 значения: ![math]() .Известно, что
.Известно, что ![math]() ,
, ![math]() ,
, ![math]() . Чему равна дисперсия
. Чему равна дисперсия ![math]() ?
?
 принимает только 4 значения:
принимает только 4 значения:  .Известно, что
.Известно, что  ,
,  ,
,  . Чему равна дисперсия
. Чему равна дисперсия  ?
?
1,04
Выберите все верные утверждения.
(1) существуют последовательности случайных величин, которые сходятся по вероятности, но не сходятся почти наверное
(2) если последовательность случайных величин сходится почти наверное, то она сходится и по вероятности
(3) если последовательность случайных величин сходится по вероятности, то она сходится и почти наверное
(4)
Пусть ![math]() , тогда для любого
, тогда для любого ![math]() , причем
, причем ![math]() и для любого
и для любого ![math]() существует
существует ![math]() , которое является
, которое является ![math]() -сетью. От чего зависит мощность
-сетью. От чего зависит мощность ![math]() ?
?
 , тогда для любого
, тогда для любого  , причем
, причем  и для любого
и для любого  существует
существует  , которое является
, которое является  -сетью. От чего зависит мощность
-сетью. От чего зависит мощность  ?
?
(1) от ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

На каком интервале значений ![math]() последовательность биномиальных коэффициентов
последовательность биномиальных коэффициентов ![math]() возрастает?
возрастает?
 последовательность биномиальных коэффициентов
последовательность биномиальных коэффициентов  возрастает?
возрастает?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой граф соответствует коду Прюфера 453376?
(1) ![files]()

(2) ![files]()

(3) ![files]()

Выберите вид рекуррентной формулы количества разбиений числа ![math]() на слагаемые, не превышающие
на слагаемые, не превышающие ![math]() .
.
 на слагаемые, не превышающие
на слагаемые, не превышающие  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

С использованием ![math]() - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция ![math]() .Чему равно значение выражения
.Чему равно значение выражения ![math]() ?
?
 - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция  .Чему равно значение выражения
.Чему равно значение выражения  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равняется кликовое число ![math]() ?
?
 ?
?
(1) 1
(2) ![math]()

(3) ![math]()

Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Чему равна вероятность события
целиком красная. Чему равна вероятность события ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Чему равна вероятность события
целиком красная. Чему равна вероятность события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая оценка для ![math]() получается с помощью локальной леммы Ловаса?
получается с помощью локальной леммы Ловаса?
 получается с помощью локальной леммы Ловаса?
получается с помощью локальной леммы Ловаса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество объектов: множество ![math]() , из которого выбираются сочетания по
, из которого выбираются сочетания по ![math]() элементов. Сколько из этих сочетаний не содержит объект
элементов. Сколько из этих сочетаний не содержит объект ![math]() ?
?
 , из которого выбираются сочетания по
, из которого выбираются сочетания по  элементов. Сколько из этих сочетаний не содержит объект
элементов. Сколько из этих сочетаний не содержит объект  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание ![math]() , если известно
, если известно ![math]()
![math]() ?
?
 , если известно
, если известно 
 ?
?
21
Какое условие выполняется для последовательности случайных величин ![math]() при
при ![math]() сходящихся по распределению к
сходящихся по распределению к ![math]() ?
?
 при
при  сходящихся по распределению к
сходящихся по распределению к  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() .Что тогда верно относительно
.Что тогда верно относительно ![math]() ?
?
 .Что тогда верно относительно
.Что тогда верно относительно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Знак ![math]() в выражении
в выражении ![math]() означает...
означает...
 в выражении
в выражении  означает...
означает...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какова асимптотическая оценка количества унициклических графов ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выберите вид рекуррентной формулы количества разбиений числа ![math]() на
на ![math]() слагаемых.
слагаемых.
 на
на  слагаемых.
слагаемых.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

С использованием ![math]() - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция ![math]() .Что верно относительно функции
.Что верно относительно функции ![math]() ?
?
 - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция  .Что верно относительно функции
.Что верно относительно функции  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно кликовое число Кнезеровского графа ![math]() ?
?
 ?
?
2
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя. Чему равна вероятность события
целиком синяя. Чему равна вероятность события ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя. Чему равна вероятность события
целиком синяя. Чему равна вероятность события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Рассмотрим случайную раскраску полного графа ![math]() на
на ![math]() вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть ![math]() -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и ![math]() - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события ![math]() , где
, где ![math]() -состоит в том, что
-состоит в том, что ![math]() -ый треугольник целиком красный и
-ый треугольник целиком красный и ![math]() -состоит в том, что
-состоит в том, что ![math]() -ая клика размера
-ая клика размера ![math]() целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события ![math]() построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины ![math]() орграфа зависимостей в вершины
орграфа зависимостей в вершины ![math]() ?
?
 на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события  , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и  -состоит в том, что
-состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события  построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины  орграфа зависимостей в вершины
орграфа зависимостей в вершины  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна дисперсия ![math]() ?
?
 ?
?
0
Пусть ![math]() - последовательность независимых в совокупности случайных величин, для которых дисперсия конечна
- последовательность независимых в совокупности случайных величин, для которых дисперсия конечна ![math]() и сходится ряд
и сходится ряд ![math]() . С каким типом сходимости
. С каким типом сходимости ![math]() сходится к
сходится к ![math]() при
при ![math]() ?
?
 - последовательность независимых в совокупности случайных величин, для которых дисперсия конечна
- последовательность независимых в совокупности случайных величин, для которых дисперсия конечна  и сходится ряд
и сходится ряд  . С каким типом сходимости
. С каким типом сходимости  сходится к
сходится к  при
при  ?
?
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
пусть ![math]() . Для
. Для ![math]() что представляет собой
что представляет собой ![math]()
 . Для
. Для  что представляет собой
что представляет собой 
(1) треугольники
(2) тетраэдры
(3) открытые полуплоскости
(4) лучи
Выберите меньшее выражение из перечисленных.
(1) ![math]()

(2) ![math]()

(3) ![math]()

В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах
вершинах ![math]() выражение
выражение ![math]() показывает...
показывает...
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах  выражение
выражение  показывает...
показывает...
(1) число способов построить цикл на выбранных вершинах
(2) число способов зафиксировать вершины для цикла
(3) число способов зафиксировать цикл
(4) число различных (как графы с занумерованными вершинами) лесов с ![math]() деревьями с общим количеством вершин
деревьями с общим количеством вершин ![math]() , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …, ![math]() -ое дерево содержит вершину
-ое дерево содержит вершину ![math]()
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину 
. Пусть ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность ![math]() и
и ![math]() , если
, если ![math]() ?
?
 - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и  - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность  и
и  , если
, если  ?
?
0
Используя операции с формальными степенными рядами, определите чему равен коэффициент при ![math]() при разложении
при разложении ![math]() в формальный степенной ряд.
в формальный степенной ряд.
 при разложении
при разложении  в формальный степенной ряд.
в формальный степенной ряд.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколько вершин содержит Кнезеровский граф ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

При каком минимальном ![math]() выполняется неравенство
выполняется неравенство ![math]() ?
?
 выполняется неравенство
выполняется неравенство  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для событий ![math]() составлено равенство
составлено равенство ![math]() . Каким должен быть последний сомножитель, чтобы это выражение было правильным?
. Каким должен быть последний сомножитель, чтобы это выражение было правильным?
 составлено равенство
составлено равенство  . Каким должен быть последний сомножитель, чтобы это выражение было правильным?
. Каким должен быть последний сомножитель, чтобы это выражение было правильным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание ![math]() ?
?
 ?
?
5
Пусть ![math]() . Чему равно
. Чему равно ![math]() ?
?
 . Чему равно
. Чему равно  ?
?
3
Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайное подмножество
выбираем случайное подмножество ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определено событие
. Пусть определено событие ![math]() . Какое события является отрицанием события
. Какое события является отрицанием события ![math]() ?
?
 . Из множества
. Из множества  выбираем случайное подмножество
выбираем случайное подмножество  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определено событие
. Пусть определено событие  . Какое события является отрицанием события
. Какое события является отрицанием события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите наибольшее выражение из перечисленных.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах
вершинах ![math]() выражение
выражение ![math]() показывает...
показывает...
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах  выражение
выражение  показывает...
показывает...
(1) число способов построить цикл на выбранных вершинах
(2) число способов зафиксировать вершины для цикла
(3) число способов зафиксировать цикл
(4) число различных (как графы с занумерованными вершинами) лесов с ![math]() деревьями с общим количеством вершин
деревьями с общим количеством вершин ![math]() , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …, ![math]() -ое дерево содержит вершину
-ое дерево содержит вершину ![math]()
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину 
Пусть ![math]() и
и ![math]() . Чему равно
. Чему равно ![math]() ?
?
 и
и  . Чему равно
. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равен четвертый член последовательности чисел Каталана?
14
Чему равно кликовое число Кнезеровского графа ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

При каком ![math]() выполняется неравенство
выполняется неравенство ![math]() ?
?
 выполняется неравенство
выполняется неравенство  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна ![math]() вероятность ровно
вероятность ровно ![math]() успехов в
успехов в ![math]() испытаниях по схеме Бернулли, если вероятность успеха в одном испытании
испытаниях по схеме Бернулли, если вероятность успеха в одном испытании ![math]() зависит от количества испытаний
зависит от количества испытаний ![math]() , зависимость
, зависимость ![math]() , где постоянная
, где постоянная ![math]() ?
?
 вероятность ровно
вероятность ровно  успехов в
успехов в  испытаниях по схеме Бернулли, если вероятность успеха в одном испытании
испытаниях по схеме Бернулли, если вероятность успеха в одном испытании  зависит от количества испытаний
зависит от количества испытаний  , зависимость
, зависимость  , где постоянная
, где постоянная  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество ![math]() и множество
и множество ![math]() – все размещения с повторениями из элементов множества по
– все размещения с повторениями из элементов множества по ![math]() по
по ![math]() . Известно, что
. Известно, что ![math]() . Рассмотрим свойство
. Рассмотрим свойство ![math]() которым или обладает или не обладает каждый элемент из множества
которым или обладает или не обладает каждый элемент из множества ![math]() . Размещение обладает свойством
. Размещение обладает свойством ![math]() , если элемент
, если элемент ![math]() не принадлежит данному размещению. Сколько
не принадлежит данному размещению. Сколько ![math]() размещений не обладает ни одним из свойств
размещений не обладает ни одним из свойств ![math]() ?
?
 и множество
и множество  – все размещения с повторениями из элементов множества по
– все размещения с повторениями из элементов множества по  по
по  . Известно, что
. Известно, что  . Рассмотрим свойство
. Рассмотрим свойство  которым или обладает или не обладает каждый элемент из множества
которым или обладает или не обладает каждый элемент из множества  . Размещение обладает свойством
. Размещение обладает свойством  , если элемент
, если элемент  не принадлежит данному размещению. Сколько
не принадлежит данному размещению. Сколько  размещений не обладает ни одним из свойств
размещений не обладает ни одним из свойств  ?
?
(1) ![math]()

(2) 1
(3) 0
(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной 0,3 проводим ребро, соответственно, с вероятностью 0,7 не проводим. Чему равна вероятность, что конкретный треугольник принадлежит случайном графу?
фиксированных вершинах, где с вероятностью равной 0,3 проводим ребро, соответственно, с вероятностью 0,7 не проводим. Чему равна вероятность, что конкретный треугольник принадлежит случайном графу?
 фиксированных вершинах, где с вероятностью равной 0,3 проводим ребро, соответственно, с вероятностью 0,7 не проводим. Чему равна вероятность, что конкретный треугольник принадлежит случайном графу?
фиксированных вершинах, где с вероятностью равной 0,3 проводим ребро, соответственно, с вероятностью 0,7 не проводим. Чему равна вероятность, что конкретный треугольник принадлежит случайном графу?
0,027
Пусть ![math]() . Чему равно
. Чему равно ![math]() ?
?
 . Чему равно
. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Что является верным относительно
. Что является верным относительно ![math]() и
и ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Что является верным относительно
. Что является верным относительно  и
и  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие функции удовлетворяют условию ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах, величина
вершинах, величина ![math]() заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![math]() Чему равна асимптотическая оценка
Чему равна асимптотическая оценка ![math]() ?
?
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина  заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых  Чему равна асимптотическая оценка
Чему равна асимптотическая оценка  ?
?
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Пусть ![math]() и
и ![math]() . Чему равен коэффициент перед
. Чему равен коэффициент перед ![math]() формального степенного ряда
формального степенного ряда ![math]() ?
?
 и
и  . Чему равен коэффициент перед
. Чему равен коэффициент перед  формального степенного ряда
формального степенного ряда  ?
?
0
Соотношение на элементы бесконечной последовательности ![math]() удовлетворяющее условию
удовлетворяющее условию ![math]() , где постоянные величины
, где постоянные величины ![math]() называется...
называется...
 удовлетворяющее условию
удовлетворяющее условию  , где постоянные величины
, где постоянные величины  называется...
называется...
(1) линейное рекуррентное соотношение с постоянными коэффициентами ![math]() -го порядка
-го порядка
 -го порядка
-го порядка
(2) линейное рекуррентное соотношение ![math]() -го порядка
-го порядка
 -го порядка
-го порядка
(3) рекуррентное соотношение с постоянными коэффициентами ![math]() -го порядка
-го порядка
 -го порядка
-го порядка
(4) соотношение с постоянными коэффициентами
Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() . Рассмотрим
. Рассмотрим ![math]() - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа ![math]() . Что верно относительно
. Что верно относительно ![math]() ?
?
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно
. Что верно относительно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определим случайную раскраску так: с вероятностью ![math]() красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью ![math]() красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Чему равна
целиком красная. Чему равна ![math]() ?
?
 красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью  красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Чему равна
целиком красная. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для событий ![math]() для любого
для любого ![math]() и любого
и любого ![math]() при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество ![math]() выполняется равенство
выполняется равенство ![math]() . Какое условие накладывается на множество
. Какое условие накладывается на множество ![math]() ?
?
 для любого
для любого  и любого
и любого  при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество  выполняется равенство
выполняется равенство  . Какое условие накладывается на множество
. Какое условие накладывается на множество  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна функция Мебиуса ![math]() , если
, если ![math]() свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение
свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение ![math]() на простые множители состоит из четного числа сомножителей?
на простые множители состоит из четного числа сомножителей?
 , если
, если  свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение
свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение  на простые множители состоит из четного числа сомножителей?
на простые множители состоит из четного числа сомножителей?
1
Пусть ![math]() . Чему равна
. Чему равна ![math]() ?
?
 . Чему равна
. Чему равна  ?
?
(1) ![math]() , где
, где ![math]() -
- ![math]() -ый факториальный момент
-ый факториальный момент
 , где
, где  -
-  -ый факториальный момент
-ый факториальный момент
(2) ![math]() , где
, где ![math]() -
- ![math]() -ый факториальный момент
-ый факториальный момент
 , где
, где  -
-  -ый факториальный момент
-ый факториальный момент
(3) ![math]() , где
, где ![math]() -
- ![math]() -ый факториальный момент
-ый факториальный момент
 , где
, где  -
-  -ый факториальный момент
-ый факториальный момент
(4) ![math]() , где
, где ![math]() -
- ![math]() -ый факториальный момент
-ый факториальный момент
 , где
, где  -
-  -ый факториальный момент
-ый факториальный момент Чему равна характеристическая функция для ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно ![math]() , где
, где ![math]() ?
?
 , где
, где  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах, величина
вершинах, величина ![math]() заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![math]() Чему равна асимптотическая оценка
Чему равна асимптотическая оценка ![math]() ?
?
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина  заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых  Чему равна асимптотическая оценка
Чему равна асимптотическая оценка  ?
?
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколько требуется знать начальных условий, чтобы однозначно определить решение для cоотношения на элементы бесконечной последовательности ![math]() удовлетворяющее условию
удовлетворяющее условию ![math]() , где постоянные величины
, где постоянные величины ![math]() ?
?
 удовлетворяющее условию
удовлетворяющее условию  , где постоянные величины
, где постоянные величины  ?
?
(1) 0
(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() . Рассмотрим
. Рассмотрим ![math]() - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа ![math]() . Допустим,
. Допустим, ![math]() . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в ![math]() кроме
кроме ![math]() ?
?
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим,  . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в  кроме
кроме  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равна вероятность события ![math]() при условии наступления события
при условии наступления события ![math]() ?
?
 при условии наступления события
при условии наступления события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность, что два человека встретятся, если они договорились, что каждый приходит в любое время в течении определенного часа, и если другого нет, ждет пятнадцать минут, потом уходит? В ответ ввести четыре знака после запятой.
0,4375
Согласно формуле обращения Мебиуса для арифметических функций ![math]() и
и ![math]() верно
верно ![math]() тогда и только тогда, когда...
тогда и только тогда, когда...
 и
и  верно
верно  тогда и только тогда, когда...
тогда и только тогда, когда...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной ![math]() проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью ![math]() не проводим. Какое максимальное число изолированных ребер имеет данный граф?
не проводим. Какое максимальное число изолированных ребер имеет данный граф?
 фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной  проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью  не проводим. Какое максимальное число изолированных ребер имеет данный граф?
не проводим. Какое максимальное число изолированных ребер имеет данный граф?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна характеристическая функция для случайной величины, равной константе ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности  ?
?
(1) ![math]() , где
, где ![math]()
 , где
, где 
(2) ![math]() , где
, где ![math]()
 , где
, где 
(3) ![math]() , где
, где ![math]()
 , где
, где 
(4) ![math]() , где
, где ![math]()
 , где
, где 
Знак ![math]() в выражении
в выражении ![math]() означает ...
означает ...
 в выражении
в выражении  означает ...
означает ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определите число различных (как графы с занумерованными вершинами) лесов с 3 деревьями с общим количеством вершин 6, такое, что первое дерево содержит вершину 1, второе – вершину 2, третье дерево содержит вершину 3.
108
Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найдите наибольшее по модулю решение характеристическое уравнение для рекуррентного соотношения ![math]() .
.
 .
.
-3
Рассмотрим Кнезеровский граф ![math]() . Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет
. Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет ![math]() все вершины, которые содержат
все вершины, которые содержат ![math]() . Элементы какого из перечисленным множества остатись не покрашенными?
. Элементы какого из перечисленным множества остатись не покрашенными?
 . Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет
. Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет  все вершины, которые содержат
все вершины, которые содержат  . Элементы какого из перечисленным множества остатись не покрашенными?
. Элементы какого из перечисленным множества остатись не покрашенными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность пересечения события ![math]() и события
и события ![math]() , если эти события независимы?
, если эти события независимы?
 и события
и события  , если эти события независимы?
, если эти события независимы?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

На перекрестке установлен автоматический светофор, в котором одну минуту горит зеленый свет и полминуты красный, затем снова одну минуту — зеленый и полминуты красный и т. д. В случайный момент времени к перекрестку подъезжает автомобиль. Какова вероятность того, что он проедет перекресток без остановки? Ответ округлить до сотых.
0,67
Как называется набор из ![math]() различных элементов некоторого
различных элементов некоторого ![math]() -элементного множества?
-элементного множества?
 различных элементов некоторого
различных элементов некоторого  -элементного множества?
-элементного множества?
(1) сочетанием из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(2) размещением из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(3) сочетанием из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(4) размещением из ![math]() элементов по n
элементов по n
 элементов по n
элементов по n Случайная величина ![math]() принимает только 3 значения:
принимает только 3 значения: ![math]() .Известно, что
.Известно, что ![math]() ,
, ![math]() . Чему равна
. Чему равна ![math]() ?
?
 принимает только 3 значения:
принимает только 3 значения:  .Известно, что
.Известно, что  ,
,  . Чему равна
. Чему равна  ?
?
0,4
Пусть ![math]() и
и ![math]() . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая ![math]()
 и
и  . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая 
0,75
Пусть ![math]() , каждая из которых принимает значение 1 с вероятностью
, каждая из которых принимает значение 1 с вероятностью ![math]() и значение 0 с вероятностью
и значение 0 с вероятностью ![math]() . Согласно усиленному закону больших чисел для схемы Бернулли к какой величине почти наверное сходится случайная величина
. Согласно усиленному закону больших чисел для схемы Бернулли к какой величине почти наверное сходится случайная величина ![math]() при
при ![math]() ?
?
 , каждая из которых принимает значение 1 с вероятностью
, каждая из которых принимает значение 1 с вероятностью  и значение 0 с вероятностью
и значение 0 с вероятностью  . Согласно усиленному закону больших чисел для схемы Бернулли к какой величине почти наверное сходится случайная величина
. Согласно усиленному закону больших чисел для схемы Бернулли к какой величине почти наверное сходится случайная величина  при
при  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какими свойствами должно бинарное отношение, которое определяет частично упорядоченное множество?
(1) рефлексивность
(2) эквивалентность
(3) транзитивность
(4) асимметричность
(5) антисимметричность
Что допускается в псевдографе?
(1) кратные ребра
(2) ничего из перечисленного
(3) петли
(4) ориентация ребер
Если раскрыть скобки в бесконечном произведении ![math]() , чему равен коэффициент при
, чему равен коэффициент при ![math]() ?
?
 , чему равен коэффициент при
, чему равен коэффициент при  ?
?
-1
Говорят, что степенной ряд ![math]() сходится в точке
сходится в точке ![math]() , если радиус ряда
, если радиус ряда ![math]() Это утверждение является...
Это утверждение является...
 сходится в точке
сходится в точке  , если радиус ряда
, если радиус ряда  Это утверждение является...
Это утверждение является...
(1) определением сходимости
(2) необходимым условием сходимости
(3) достаточным условием сходимости
(4) критерием сходимости
Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер. Подмножество
– множество ребер. Подмножество ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() принадлежит
принадлежит ![math]() .
.
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер. Подмножество
– множество ребер. Подмножество  называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  принадлежит
принадлежит  .
.
(1) клика
(2) независимое множество
(3) зависимое множество
(4) хроматическое множество
Чему равна вероятность элементарного исхода при бросании стандартной игральной кости согласно классическому определению вероятности? (Два знака после запятой).
0,17
Что согласно локальной леммы Ловаса является верным для событий, определенныx следующим образом? Пусть ![math]() события, для каждого из которых выполнено
события, для каждого из которых выполнено ![math]() и любое событие
и любое событие ![math]() независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем ![math]() штук, причем и
штук, причем и ![math]() .Тогда ...
.Тогда ...
 события, для каждого из которых выполнено
события, для каждого из которых выполнено  и любое событие
и любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук, причем и
штук, причем и  .Тогда ...
.Тогда ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

Имеются два множества непересекающихся объектов: множество ![math]() и множество
и множество ![math]() .Количество способов выбрать один объект из множества
.Количество способов выбрать один объект из множества ![math]() и один объект из множества
и один объект из множества ![math]() определяется ..
определяется ..
 и множество
и множество  .Количество способов выбрать один объект из множества
.Количество способов выбрать один объект из множества  и один объект из множества
и один объект из множества  определяется ..
определяется ..
(1) по правилу умножения и равно ![math]()

(2) по правилу сложения и равно ![math]()

(3) по правилу умножения и равно ![math]()

(4) по правилу сложения и равно ![math]()

(5) по принципу Дирихле и равно ![math]()

(6) по принципу Дирихле и равно ![math]()

Выберите абсолютно непрерывные распределения из перечисленных.
(1) нормальное распределение
(2) распределение Бернулли
(3) экспоненциальное распределение
(4) геометрическое распределение
Пусть ![math]() -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из ![math]() вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью ![math]() , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от ![math]() . Если
. Если ![math]() , то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Если
. Если  , то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
0
Пусть ![math]() бесконечная последовательность независимых событий:
бесконечная последовательность независимых событий: ![math]() . Положим
. Положим ![math]() . Тогда с каким самым сильным из предложенных типом сходимости при
. Тогда с каким самым сильным из предложенных типом сходимости при ![math]() случайная величина
случайная величина ![math]() сходится к 0?
сходится к 0?
 бесконечная последовательность независимых событий:
бесконечная последовательность независимых событий:  . Положим
. Положим  . Тогда с каким самым сильным из предложенных типом сходимости при
. Тогда с каким самым сильным из предложенных типом сходимости при  случайная величина
случайная величина  сходится к 0?
сходится к 0?
(1) по распределению
(2) по вероятности
(3) почти наверное
(4) в среднем
Пусть![math]() . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов ![math]() функцию
функцию ![math]() , где
, где ![math]() . Пусть
. Пусть ![math]() обозначает число элементов множества
обозначает число элементов множества ![math]() , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств ![math]() , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно![math]() ?
?
 . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов  функцию
функцию  , где
, где  . Пусть
. Пусть  обозначает число элементов множества
обозначает число элементов множества  , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств  , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколько ребер имеет дерево с 10 вершинами?
9
Сколько существует разложений натурального числа 9 в виде упорядоченной суммы натуральных слагаемых?
256
Если говорить о ![math]() и
и ![math]() как о производящих функциях, какие из перечисленных утверждений являются верными?
как о производящих функциях, какие из перечисленных утверждений являются верными?
 и
и  как о производящих функциях, какие из перечисленных утверждений являются верными?
как о производящих функциях, какие из перечисленных утверждений являются верными?
(1) радиус сходимости равен 1
(2) функции различаются
(3) функции совпадают
(4) при ![math]() равны 1
равны 1
 равны 1
равны 1 Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.Кликовое число графа -
– множество ребер.Кликовое число графа -
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.Кликовое число графа -
– множество ребер.Кликовое число графа -
(1) минимальное число цветов, в которые можно покрасить вершины, так чтобы любые две вершины, соединенные ребром были покрашены в разные цвета
(2) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() принадлежит
принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  принадлежит
принадлежит 
(3) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() не принадлежит
не принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  не принадлежит
не принадлежит 
Определите все элементарные исходы, которые при бросании монеты образуют событие, что выпало четное число очков.
(1) выпало 1 очко
(2) выпало 2 очка
(3) выпало 3 очка
(4) выпало 4 очка
(5) выпало 5 очков
(6) выпало 6 очков
Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. При каком условии событие
целиком красная. При каком условии событие ![math]() независит от совокупности всех
независит от совокупности всех ![math]() ?
?
 состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. При каком условии событие
целиком красная. При каком условии событие  независит от совокупности всех
независит от совокупности всех  ?
?
(1) если ![math]() -я клика имеет не более 1 общего ребра с
-я клика имеет не более 1 общего ребра с ![math]() -й кликой.
-й кликой.
 -я клика имеет не более 1 общего ребра с
-я клика имеет не более 1 общего ребра с  -й кликой.
-й кликой.
(2) если ![math]() -я клика имеет не более 1 общей вершины с
-я клика имеет не более 1 общей вершины с ![math]() -й кликой.
-й кликой.
 -я клика имеет не более 1 общей вершины с
-я клика имеет не более 1 общей вершины с  -й кликой.
-й кликой.
(3) если ![math]() -я клика имеет не более 2 общих вершин с
-я клика имеет не более 2 общих вершин с ![math]() -й кликой.
-й кликой.
 -я клика имеет не более 2 общих вершин с
-я клика имеет не более 2 общих вершин с  -й кликой.
-й кликой.
(4) если ![math]() -я клика имеет не более 2 общих ребер с
-я клика имеет не более 2 общих ребер с ![math]() -й кликой.
-й кликой.
 -я клика имеет не более 2 общих ребер с
-я клика имеет не более 2 общих ребер с  -й кликой.
-й кликой. Какая формула определяет количество сочетаний из ![math]() элементов по
элементов по ![math]() с повторениями?
с повторениями?
 элементов по
элементов по  с повторениями?
с повторениями?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Что означает запись ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() - случайный граф, множество, состоящее из
- случайный граф, множество, состоящее из ![math]() вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью ![math]() , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от ![math]() . Если
. Если ![math]() , то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
 - случайный граф, множество, состоящее из
- случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Если
. Если  , то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
, то к чему ассимптотически стремиться вероятность того, что в случайном графе есть хотя бы один треугольник?
1
Рассмотрим пару ![math]() , где
, где ![math]() - любое множество,
- любое множество, ![math]() - совокупность подмножеств в
- совокупность подмножеств в ![math]() . Что представляет собой пара
. Что представляет собой пара ![math]() ?
?
 , где
, где  - любое множество,
- любое множество,  - совокупность подмножеств в
- совокупность подмножеств в  . Что представляет собой пара
. Что представляет собой пара  ?
?
(1) однородный гиперграф
(2) граф
(3) ранжированное пространство
(4) топологическое пространство
Пусть задано частично упорядоченное множество (ЧУМ) ![math]() , и для каждого элемента
, и для каждого элемента ![math]() найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса ![math]() на ЧУМ
на ЧУМ ![math]() , если
, если ![math]() ?
?
 , и для каждого элемента
, и для каждого элемента  найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса  на ЧУМ
на ЧУМ  , если
, если  ?
?
0
Чему равно ![math]() - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на ![math]() вершинах?
вершинах?
 - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на  вершинах?
вершинах?
125
Сколько существует разложений натурального числа 9 в виде упорядоченной суммы натуральных слагаемых длины ровно 3?
28
Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.
– множество ребер.![math]() хроматическое число и
хроматическое число и ![math]() - кликовое число. Какое утверждение является верным?
- кликовое число. Какое утверждение является верным?
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. хроматическое число и
хроматическое число и  - кликовое число. Какое утверждение является верным?
- кликовое число. Какое утверждение является верным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Числом Рамсея ![math]() называется минимальное число
называется минимальное число ![math]() такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа ![math]() в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф ![math]() , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф ![math]() , у которого все ребра синие. Чему равно
, у которого все ребра синие. Чему равно ![math]() ?
?
 называется минимальное число
называется минимальное число  такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа  в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф  , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф  , у которого все ребра синие. Чему равно
, у которого все ребра синие. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Рассмотрим 30 шестиэлементных множеств ![math]() , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие ![math]() означает, что
означает, что ![math]() множество одноцветно. Чему равна
множество одноцветно. Чему равна ![math]() ?
?
 , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие  означает, что
означает, что  множество одноцветно. Чему равна
множество одноцветно. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равен биномиальный коэффициент перед выражением ![math]() при разложении
при разложении ![math]() ?
?
 при разложении
при разложении  ?
?
21
Что означает запись ![math]() ?
?
 ?
?
(1)
(2)
(3)
(4) ![math]()

Требуется оценить вероятность ![math]() . Что получиться в результате применения неравенства Маркова?
. Что получиться в результате применения неравенства Маркова?
 . Что получиться в результате применения неравенства Маркова?
. Что получиться в результате применения неравенства Маркова?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим ранжированное пространство ![math]() , где
, где ![math]() - множество всех закрытых полупространств в
- множество всех закрытых полупространств в ![math]() . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для ![math]() ?
?
 , где
, где  - множество всех закрытых полупространств в
- множество всех закрытых полупространств в  . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для  ?
?
2
Пусть отношение «… делитель…» определяет частичный порядок на множестве ![math]() . Чему равно значение элемента, который является непосредственным предшественником элемента, равного 12?
. Чему равно значение элемента, который является непосредственным предшественником элемента, равного 12?
 . Чему равно значение элемента, который является непосредственным предшественником элемента, равного 12?
. Чему равно значение элемента, который является непосредственным предшественником элемента, равного 12?
6
На рисунке представлено дерево. Укажите код Прюфера, соответствующий данному дереву (записывать как число без запятых и пробелов).
![files]()

1455
Сколько существует диаграмм Юнга произвольного веса, но имеющих не более 5 строк и 3 столбцов?
55
Чему равен седьмой член последовательности, если![math]() ?
?
 ?
?
13
Рассмотрим множество ![math]() - множество всех графов на
- множество всех графов на ![math]() вершинах. Чему равна мощность множества
вершинах. Чему равна мощность множества ![math]()
 - множество всех графов на
- множество всех графов на  вершинах. Чему равна мощность множества
вершинах. Чему равна мощность множества 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая формула эквивалентна следующему высказыванию относительно чисел Рамсея: существует раскраска ребер полного графа ![math]() , при которой нет ни одной красной клики
, при которой нет ни одной красной клики ![math]() и ни одной синей клики
и ни одной синей клики ![math]() ?
?
 , при которой нет ни одной красной клики
, при которой нет ни одной красной клики  и ни одной синей клики
и ни одной синей клики  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() .Пусть
.Пусть ![math]()
![math]() -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем ![math]() множествам
множествам ![math]() , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного ![math]() -элементного подмножества. При применении к данной ситуации локальной леммы Ловаса чему равно
-элементного подмножества. При применении к данной ситуации локальной леммы Ловаса чему равно ![math]() ?
?
 .Пусть
.Пусть 
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем  множествам
множествам  , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного  -элементного подмножества. При применении к данной ситуации локальной леммы Ловаса чему равно
-элементного подмножества. При применении к данной ситуации локальной леммы Ловаса чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколькими способами можно переставить буквы в слове «КАСКА» так, чтобы получилось новое слово (возможно бессмысленное)?
30
Случайная величина ![math]() принимает только 4 значения:
принимает только 4 значения: ![math]() .Известно, что
.Известно, что ![math]() ,
, ![math]() ,
, ![math]() . Чему равно математическое ожидание
. Чему равно математическое ожидание ![math]() ?
?
 принимает только 4 значения:
принимает только 4 значения:  .Известно, что
.Известно, что  ,
,  ,
,  . Чему равно математическое ожидание
. Чему равно математическое ожидание  ?
?
2,4
Пусть случайные величины ![math]() , определенные на некотором
, определенные на некотором ![math]() . Если выполняется условие
. Если выполняется условие ![math]() , то говорят, что
, то говорят, что ![math]() сходится к
сходится к ![math]() ...
...
 , определенные на некотором
, определенные на некотором  . Если выполняется условие
. Если выполняется условие  , то говорят, что
, то говорят, что  сходится к
сходится к  ...
...
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Согласно теореме Радона какое условие из перечисленных выполняется, если ![math]() и
и ![math]() ?
?
 и
и  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Журнал А читают 70% студентов, журнал В – 40% студентов, журнал С – 50% студентов; 30% студентов читают журналы А и В, 40% - журналы А и С, 20% - журналы В и С, 10% - журналы А, В и С. Сколько процентов студентов не читают не одного из журналов А, В и С?
20
Сколько циклов содержит связный унициклический граф с 5 вершинами?
1
Какой знак можно поставить между числом упорядоченных разбиений числа ![math]() на
на ![math]() слагаемых и числом упорядоченных разбиений числа
слагаемых и числом упорядоченных разбиений числа ![math]() ?
?
 на
на  слагаемых и числом упорядоченных разбиений числа
слагаемых и числом упорядоченных разбиений числа  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равен четвертый член последовательности числе Фибоначчи?
3
Что является Кнезеровским графом ![math]() ?
?
 ?
?
(1) граф Эйлера
(2) паросочетание
(3) полный граф на ![math]() вершинах
вершинах
 вершинах
вершинах
(4) граф Петерсена
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Событие
целиком красная. Событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя.Что является формальным описанием следующего события: существует клика размера
целиком синяя.Что является формальным описанием следующего события: существует клика размера ![math]() целиком красная или существует клика размера
целиком красная или существует клика размера ![math]() целиком синяя?
целиком синяя?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Событие
целиком красная. Событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя.Что является формальным описанием следующего события: существует клика размера
целиком синяя.Что является формальным описанием следующего события: существует клика размера  целиком красная или существует клика размера
целиком красная или существует клика размера  целиком синяя?
целиком синяя?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

 - события. Пусть
- события. Пусть  произвольный орграф зависимостей и существуют
произвольный орграф зависимостей и существуют  такие, что для любого
такие, что для любого  выполнено
выполнено  . Тогда ...
. Тогда ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выберите выражение равное ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна дисперсия для ![math]() ?
?
 ?
?
2
Какой тип сходимости фигурирует в теореме Муавра-Лапласа?
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Пусть ![math]() , тогда для любого
, тогда для любого ![math]() , причем
, причем ![math]() и для любого
и для любого ![math]() существует
существует ![math]() , которое является
, которое является ![math]() -сетью. Что верно относительно мощности
-сетью. Что верно относительно мощности ![math]() ?
?
 , тогда для любого
, тогда для любого  , причем
, причем  и для любого
и для любого  существует
существует  , которое является
, которое является  -сетью. Что верно относительно мощности
-сетью. Что верно относительно мощности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

На каком интервале значений ![math]() последовательность биномиальных коэффициентов
последовательность биномиальных коэффициентов ![math]() убывает?
убывает?
 последовательность биномиальных коэффициентов
последовательность биномиальных коэффициентов  убывает?
убывает?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой граф соответствует коду Прюфера 171716?
(1) ![files]()

(2) ![files]()

(3) ![files]()

Выберите все начальные условия соответствующие рекуррентной формулы количества разбиений числа ![math]() на слагаемые, не превышающие
на слагаемые, не превышающие ![math]() .
.
 на слагаемые, не превышающие
на слагаемые, не превышающие  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

С использованием ![math]() - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция ![math]() .Чему равно значение выражения
.Чему равно значение выражения ![math]() ?
?
 - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция  .Чему равно значение выражения
.Чему равно значение выражения  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равняется хроматическое число ![math]() ?
?
 ?
?
(1) 1
(2) ![math]()

(3) ![math]()

Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Событие
в два цвета - красный и синий. Событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя.Чему равна вероятность события
целиком синяя.Чему равна вероятность события ![math]() ?
?
 в два цвета - красный и синий. Событие
в два цвета - красный и синий. Событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя.Чему равна вероятность события
целиком синяя.Чему равна вероятность события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Рассмотрим случайную раскраску полного графа ![math]() на
на ![math]() вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть ![math]() -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и ![math]() - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события ![math]() , где
, где ![math]() -состоит в том, что
-состоит в том, что ![math]() -ый треугольник целиком красный и
-ый треугольник целиком красный и ![math]() -состоит в том, что
-состоит в том, что ![math]() -ая клика размера
-ая клика размера ![math]() целиком синяя. Чему равна
целиком синяя. Чему равна ![math]() ?
?
 на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события  , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и  -состоит в том, что
-состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Чему равна
целиком синяя. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() – последовательность из 0 и 1 длины
– последовательность из 0 и 1 длины ![math]() . Найдите
. Найдите ![math]() .
.
 – последовательность из 0 и 1 длины
– последовательность из 0 и 1 длины  . Найдите
. Найдите  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание ![math]() , если известно
, если известно ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() - независимые случайные величины?
- независимые случайные величины?
 , если известно
, если известно  ,
,  ,
,  и
и  - независимые случайные величины?
- независимые случайные величины?
15
Какой тип сходимости фигурирует в усиленом законе больших чисел в формулировке Колмогорова?
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Пусть ![math]() .Что тогда верно относительно
.Что тогда верно относительно ![math]() ?
?
 .Что тогда верно относительно
.Что тогда верно относительно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна асимптотическая оценка ![math]() согласно формуле Стирлинга?
согласно формуле Стирлинга?
 согласно формуле Стирлинга?
согласно формуле Стирлинга?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какова точная оценка количества унициклических графов ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выберите все начальные условия соответствующие рекуррентной формуле количества разбиений числа ![math]() на
на ![math]() слагаемых.
слагаемых.
 на
на  слагаемых.
слагаемых.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

С использованием ![math]() - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция ![math]() .Что верно относительно функции
.Что верно относительно функции ![math]() ?
?
 - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция  .Что верно относительно функции
.Что верно относительно функции  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно хроматическое число Кнезеровского графа ![math]() ?
?
 ?
?
3
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Чему равно
целиком красная. Чему равно ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Чему равно
целиком красная. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим случайную раскраску полного графа ![math]() на
на ![math]() вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть ![math]() -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и ![math]() - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события ![math]() , где
, где ![math]() -состоит в том, что
-состоит в том, что ![math]() -ый треугольник целиком красный и
-ый треугольник целиком красный и ![math]() -состоит в том, что
-состоит в том, что ![math]() -ая клика размера
-ая клика размера ![math]() целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события ![math]() построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины ![math]() орграфа зависимостей в вершины
орграфа зависимостей в вершины ![math]() ?
?
 на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события  , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и  -состоит в том, что
-состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события  построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины  орграфа зависимостей в вершины
орграфа зависимостей в вершины  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна дисперсия ![math]() , если известно
, если известно ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() - независимые случайные величины?
- независимые случайные величины?
 , если известно
, если известно  ,
,  ,
,  и
и  - независимые случайные величины?
- независимые случайные величины?
59
Имеется бесконечная последовательность одинаково распределенных и независимых случайных величин ![math]() . Обозначим
. Обозначим ![math]() . Тогда с каким типом сходимости при
. Тогда с каким типом сходимости при ![math]() случайная величина
случайная величина ![math]() сходится к
сходится к ![math]() ?
?
 . Обозначим
. Обозначим  . Тогда с каким типом сходимости при
. Тогда с каким типом сходимости при  случайная величина
случайная величина  сходится к
сходится к  ?
?
(1) по распределению
(2) по вероятности
(3) почти наверное
(4) в среднем
Пусть ![math]() .Пусть
.Пусть ![math]() . Что тогда верно относительно
. Что тогда верно относительно ![math]() ?
?
 .Пусть
.Пусть  . Что тогда верно относительно
. Что тогда верно относительно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выберите наибольшее выражение из перечисленных.
(1) ![math]()

(2) ![math]()

(3) ![math]()

В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах
вершинах ![math]() выражение
выражение ![math]() показывает...
показывает...
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах  выражение
выражение  показывает...
показывает...
(1) число способов построить цикл на выбранных вершинах
(2) число способов зафиксировать вершины для цикла
(3) число способов зафиксировать цикл
(4) число различных (как графы с занумерованными вершинами) лесов с ![math]() деревьями с общим количеством вершин
деревьями с общим количеством вершин ![math]() , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …, ![math]() -ое дерево содержит вершину
-ое дерево содержит вершину ![math]()
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину 
Пусть ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность ![math]() и
и ![math]() , если
, если ![math]() ?
?
 - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и  - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность  и
и  , если
, если  ?
?
-1
Используя операции с формальными степенными рядами, определите чему равен коэффициент при ![math]() при разложении
при разложении ![math]() в формальный степенной ряд.
в формальный степенной ряд.
 при разложении
при разложении  в формальный степенной ряд.
в формальный степенной ряд.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно хроматическое число Кнезеровского графа ![math]() ?
?
 ?
?
2
Если ![math]() , то какой знак можно поставить между
, то какой знак можно поставить между ![math]() и 1?
и 1?
 , то какой знак можно поставить между
, то какой знак можно поставить между  и 1?
и 1?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для событий ![math]() составлено равенство
составлено равенство ![math]() Каким должен быть последний сомножитель, чтобы это выражение было правильным?
Каким должен быть последний сомножитель, чтобы это выражение было правильным?
 составлено равенство
составлено равенство  Каким должен быть последний сомножитель, чтобы это выражение было правильным?
Каким должен быть последний сомножитель, чтобы это выражение было правильным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество объектов ![math]() , из которого выбираются сочетания по
, из которого выбираются сочетания по ![math]() элементов. Из множества всех возможных сочетаний выбрали подмножество
элементов. Из множества всех возможных сочетаний выбрали подмножество ![math]() , в котором ровно
, в котором ровно ![math]() элементов принадлежат
элементов принадлежат ![math]() .Найдите мощность
.Найдите мощность ![math]() .
.
 , из которого выбираются сочетания по
, из которого выбираются сочетания по  элементов. Из множества всех возможных сочетаний выбрали подмножество
элементов. Из множества всех возможных сочетаний выбрали подмножество  , в котором ровно
, в котором ровно  элементов принадлежат
элементов принадлежат  .Найдите мощность
.Найдите мощность  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание ![math]() , которое равно номеру первого успеха?
, которое равно номеру первого успеха?
 , которое равно номеру первого успеха?
, которое равно номеру первого успеха?
5
Пусть ![math]() . Чему равно
. Чему равно ![math]() ?
?
 . Чему равно
. Чему равно  ?
?
1
Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какой знак можно поставить между
. Какой знак можно поставить между ![math]() и
и ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какой знак можно поставить между
. Какой знак можно поставить между  и
и  ?
?
(1) меньше
(2) больше
(3) равно
Выберите функцию равную ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах
вершинах ![math]() выражение
выражение ![math]() показывает...
показывает...
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах  выражение
выражение  показывает...
показывает...
(1) число способов построить цикл на выбранных вершинах
(2) число способов зафиксировать вершины для цикла
(3) число способов зафиксировать цикл
(4) число различных (как графы с занумерованными вершинами) лесов с ![math]() деревьями с общим количеством вершин
деревьями с общим количеством вершин ![math]() , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …, ![math]() -ое дерево содержит вершину
-ое дерево содержит вершину ![math]()
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину 
Пусть ![math]() и
и ![math]() . Чему равен коэффициент перед
. Чему равен коэффициент перед ![math]() формального степенного ряда
формального степенного ряда ![math]() ?
?
 и
и  . Чему равен коэффициент перед
. Чему равен коэффициент перед  формального степенного ряда
формального степенного ряда  ?
?
2
Чему равен пятый член последовательности чисел Каталана?
42
Чему равно число независимости Кнезеровского графа ![math]() , если
, если ![math]() ?
?
 , если
, если  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Что верно относительно ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему согласно теореме Муавра-Лапласа равна ![math]() , если
, если ![math]() - число испытаний,
- число испытаний, ![math]() - вероятность успеха в одном испытании,
- вероятность успеха в одном испытании, ![math]() - вероятность неудачи в одном испытании,
- вероятность неудачи в одном испытании, ![math]() -число успехов в
-число успехов в ![math]() испытаниях?
испытаниях?
 , если
, если  - число испытаний,
- число испытаний,  - вероятность успеха в одном испытании,
- вероятность успеха в одном испытании, 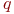 - вероятность неудачи в одном испытании,
- вероятность неудачи в одном испытании,  -число успехов в
-число успехов в  испытаниях?
испытаниях?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно значение выражения ![math]() при
при ![math]() ?
?
 при
при  ?
?
(1) -1
(2) 1
(3) 0
(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной ![math]() проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью ![math]() не проводим. Чему равно максимальное число треугольников, которые можно построить на графе на
не проводим. Чему равно максимальное число треугольников, которые можно построить на графе на ![math]() вершинах?
вершинах?
 фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной  проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью  не проводим. Чему равно максимальное число треугольников, которые можно построить на графе на
не проводим. Чему равно максимальное число треугольников, которые можно построить на графе на  вершинах?
вершинах?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Чему равно
. Чему равно ![math]() ?
?
 . Чему равно
. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Чему равна вероятность
. Чему равна вероятность ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Чему равна вероятность
. Чему равна вероятность  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая запись равносильна записи ![math]() , где постоянная
, где постоянная ![math]() ?
?
 , где постоянная
, где постоянная  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах, величина
вершинах, величина ![math]() заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![math]() .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки ![math]()
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина  заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых  .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки 
(1) замена ![math]()

(2) сумма арифметической прогрессии
(3) сумма геометрической прогрессии
(4) свойство ![math]()

(5) свойство ![math]()

Пусть ![math]() и
и ![math]() . Чему равен коэффициент перед
. Чему равен коэффициент перед ![math]() формального степенного ряда
формального степенного ряда ![math]() ?
?
 и
и  . Чему равен коэффициент перед
. Чему равен коэффициент перед  формального степенного ряда
формального степенного ряда  ?
?
1
Выберите какими свойствами cоотношение на элементы бесконечной последовательности ![math]() удовлетворяющее условию
удовлетворяющее условию ![math]() , где постоянные величины
, где постоянные величины ![math]() .
.
 удовлетворяющее условию
удовлетворяющее условию  , где постоянные величины
, где постоянные величины  .
.
(1) линейность
(2) нелинейность
(3) логлинейность
(4) сублинейность
Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() . Рассмотрим
. Рассмотрим ![math]() - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа ![math]() . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности ![math]() ?
?
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определим случайную раскраску так: с вероятностью ![math]() красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью ![math]() красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя. Чему равна
целиком синяя. Чему равна ![math]() ?
?
 красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью  красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя. Чему равна
целиком синяя. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для событий ![math]() для любого
для любого ![math]() и любого
и любого ![math]() при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество ![math]() выполняется равенство
выполняется равенство ![math]() . Какое условие накладывается на множество
. Какое условие накладывается на множество ![math]() ?
?
 для любого
для любого  и любого
и любого  при выполнении некоторого ограничения на множество
при выполнении некоторого ограничения на множество  выполняется равенство
выполняется равенство  . Какое условие накладывается на множество
. Какое условие накладывается на множество  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна функция Мебиуса ![math]() , если
, если ![math]() свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение
свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение ![math]() на простые множители состоит из нечетного числа сомножителей?
на простые множители состоит из нечетного числа сомножителей?
 , если
, если  свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение
свободно от квадратов (то есть не делится на квадрат никакого простого числа) и разложение  на простые множители состоит из нечетного числа сомножителей?
на простые множители состоит из нечетного числа сомножителей?
-1
Пусть дана последовательность случайных величин ![math]() . Пусть
. Пусть ![math]() . Чему равно
. Чему равно ![math]() при
при ![math]() ?
?
 . Пусть
. Пусть  . Чему равно
. Чему равно  при
при  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется бесконечная последовательность одинаковораспределенных и независимых случайных величин ![math]() . Обозначим
. Обозначим ![math]() . Чему равна характеристическая функция для
. Чему равна характеристическая функция для ![math]() ?
?
 . Обозначим
. Обозначим  . Чему равна характеристическая функция для
. Чему равна характеристическая функция для  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна энтропия ![math]() для
для ![math]() , где
, где ![math]() ?
?
 для
для  , где
, где  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах, величина
вершинах, величина ![math]() заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![math]() .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки ![math]()
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина  заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых  .Выберите операции и свойства, которые использовались для нахождения асимптотической оценки
.Выберите операции и свойства, которые использовались для нахождения асимптотической оценки 
(1) замена ![math]()

(2) сумма арифметической прогрессии
(3) сумма геометрической прогрессии
(4) свойство ![math]()

(5) свойство ![math]()

Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Как выглядит характеристическое уравнение для cоотношения на элементы бесконечной последовательности ![math]() удовлетворяющее условию
удовлетворяющее условию ![math]() , где постоянные величины
, где постоянные величины ![math]() , если
, если ![math]() ?
?
 удовлетворяющее условию
удовлетворяющее условию  , где постоянные величины
, где постоянные величины  , если
, если  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() .Среди множеств
.Среди множеств ![math]() и
и ![math]() выберите множество, с котором не пересекается
выберите множество, с котором не пересекается ![math]() .
.
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств  и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность события ![math]() при условии наступления события
при условии наступления события ![math]() ?
?
 при условии наступления события
при условии наступления события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность, что два человека встретятся, если они договорились, что каждый приходит в любое время в течении определенного часа, и если другого нет, ждет двадцать минут, потом уходит? В ответ ввести четыре знака после запятой, остальные знаки отбросить.
0,5555
Согласно формуле обращения Мебиуса для арифметических функций ![math]() и
и ![math]() верно
верно ![math]() тогда и только тогда, когда...
тогда и только тогда, когда...
 и
и  верно
верно  тогда и только тогда, когда...
тогда и только тогда, когда...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной ![math]() проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью ![math]() не проводим. Пусть
не проводим. Пусть ![math]() - число изолированных ребер в графе
- число изолированных ребер в графе ![math]() Чему равно математическое ожидание
Чему равно математическое ожидание ![math]() ?
?
 фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной  проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью  не проводим. Пусть
не проводим. Пусть  - число изолированных ребер в графе
- число изолированных ребер в графе  Чему равно математическое ожидание
Чему равно математическое ожидание  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется бесконечная последовательность одинаково распределенных и независимых случайных величин ![math]() , у которых математическое ожидание конечно
, у которых математическое ожидание конечно![math]() . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при ![math]() последоваетельность случайных величин
последоваетельность случайных величин ![math]() сходится к
сходится к ![math]() ?
?
 , у которых математическое ожидание конечно
, у которых математическое ожидание конечно . C каким самым сильным типом сходимости при
. C каким самым сильным типом сходимости при  последоваетельность случайных величин
последоваетельность случайных величин  сходится к
сходится к  ?
?
(1) по распределению
(2) по вероятности
(3) почти наверное
(4) в среднем
Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какое утверждения является верным относительно вероятности
. Какое утверждения является верным относительно вероятности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() эквивалента функции
эквивалента функции ![math]() асимптотически означает, что ...
асимптотически означает, что ...
 эквивалента функции
эквивалента функции  асимптотически означает, что ...
асимптотически означает, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определите число различных (как графы с занумерованными вершинами) лесов с 4 деревьями с общим количеством вершин 6, такое, что первое дерево содержит вершину 1, второе – вершину 2, третье дерево содержит вершину 3, четвертое дерево содержит вершину 4.
24
Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найдите наибольшее по модулю решение характеристическое уравнение для рекуррентного соотношения ![math]()

3
Что является верным относительно хроматического числа Кнезеровского графа ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В двух урнах находится соответственно 4 и 5 белых и 6 и 3 черных шаров. Из каждой урны наудачу извлекается один шар, а затем из этих двух наудачу берется один. Какова вероятность, что это будет белый шар? Ответ округлить до сотых.
0,51
К автобусной остановке через каждые четыре минуты подходит автобус линии А и через каждые шесть минут — автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего автобуса линии В равновозможен в пределах от нуля до четырех минут. Определить вероятность того, что первый пришедший автобус окажется автобусом линии А. Ответ округлить до сотых.
0,67
Как называется упорядоченный набор из ![math]() различных элементов некоторого
различных элементов некоторого ![math]() -элементного множества, если элементы выбираются с повторениями?
-элементного множества, если элементы выбираются с повторениями?
 различных элементов некоторого
различных элементов некоторого  -элементного множества, если элементы выбираются с повторениями?
-элементного множества, если элементы выбираются с повторениями?
(1) сочетанием с повторениями из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(2) сочетанием с повторениями из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(3) размещением с повторениями из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
(4) размещением с повторениями из ![math]() элементов по
элементов по ![math]()
 элементов по
элементов по 
Случайная величина ![math]() принимает только 3 значения:
принимает только 3 значения: ![math]() .Известно, что
.Известно, что ![math]() ,
, ![math]() . Чему равна
. Чему равна ![math]() ?
?
 принимает только 3 значения:
принимает только 3 значения:  .Известно, что
.Известно, что  ,
,  . Чему равна
. Чему равна  ?
?
0,3
Пусть ![math]() и
и ![math]() . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая ![math]()
 и
и  . Какое число будет стоять в правой части неравенства Маркова для этого случая
. Какое число будет стоять в правой части неравенства Маркова для этого случая 
0,5
Пусть ![math]() , каждая из которых принимает значение 1 с вероятностью
, каждая из которых принимает значение 1 с вероятностью ![math]() и значение 0 с вероятностью
и значение 0 с вероятностью ![math]() . Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина
. Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина ![math]() сходится при
сходится при ![math]() к
к ![math]() ?
?
 , каждая из которых принимает значение 1 с вероятностью
, каждая из которых принимает значение 1 с вероятностью  и значение 0 с вероятностью
и значение 0 с вероятностью  . Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина
. Согласно усиленному закону больших чисел для схемы Бернулли c каким самым сильным типом сходимости случайная величина  сходится при
сходится при  к
к  ?
?
(1) по распределению
(2) по вероятности
(3) почти наверное
(4) в среднем
Какое отношение позволяет задать на множестве ![math]() частично упорядоченное множество?
частично упорядоченное множество?
 частично упорядоченное множество?
частично упорядоченное множество?
(1) объединение
(2) пересечение
(3) исключение
(4) включение
Что допускается в мультиграфе?
(1) кратные ребра
(2) ничего из перечисленного
(3) петли
(4) ориентация ребер
Если раскрыть скобки в бесконечном произведении ![math]() , чему равен коэффициент при
, чему равен коэффициент при ![math]() ?
?
 , чему равен коэффициент при
, чему равен коэффициент при  ?
?
1
Говорят, что степенной ряд ![math]() сходится в точке
сходится в точке ![math]() , если
, если ![math]() , где радиус ряда
, где радиус ряда ![math]() Это утверждение является...
Это утверждение является...
 сходится в точке
сходится в точке  , если
, если  , где радиус ряда
, где радиус ряда  Это утверждение является...
Это утверждение является...
(1) определением сходимости
(2) необходимым условием сходимости
(3) достаточным условием сходимости
(4) критерием сходимости
Чего НЕ содержит простой граф?
(1) петель
(2) кратных ребер
(3) ориентации
Чему равна вероятность элементарного исхода при бросании стандартной монеты согласно классическому определению вероятности? (Один знак после запятой).
0,5
Что согласно локальной леммы Ловаса является верным для событий, определенныx следующим образом? Пусть ![math]() события, для каждого из которых выполнено
события, для каждого из которых выполнено ![math]() и любое событие
и любое событие ![math]() независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем ![math]() штук, причем и
штук, причем и ![math]() .Тогда ...
.Тогда ...
 события, для каждого из которых выполнено
события, для каждого из которых выполнено  и любое событие
и любое событие  независит от остальных событий кроме не более чем
независит от остальных событий кроме не более чем  штук, причем и
штук, причем и  .Тогда ...
.Тогда ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

Имеются два множества объектов: множество объектов («кроликов») и множество контейнеров («ящиков»). Утверждение, позволяющее установить связь между объектами и контейнерами определяется ...
(1) правилом сложения
(2) принципом Дирихле
(3) правилом умножения
Выберите дискретные распределения из перечисленных.
(1) экспоненциальное распределение
(2) распределение Вейбулла
(3) вырожденное распределение
(4) биномиальное распределение
Пусть ![math]() -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из ![math]() вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью ![math]() , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от ![math]() . Пусть случайная величина
. Пусть случайная величина ![math]() - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если ![math]() , то к чему ассимтотические стремится математическое ожидание
, то к чему ассимтотические стремится математическое ожидание ![math]() ?
?
 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Пусть случайная величина
. Пусть случайная величина  - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если  , то к чему ассимтотические стремится математическое ожидание
, то к чему ассимтотические стремится математическое ожидание  ?
?
0
Пусть случайное событие определено так ![math]() . Имеется
. Имеется ![math]() бесконечная последовательность событий. Тогда к чему
бесконечная последовательность событий. Тогда к чему ![math]() сходится почти наверное?
сходится почти наверное?
 . Имеется
. Имеется  бесконечная последовательность событий. Тогда к чему
бесконечная последовательность событий. Тогда к чему  сходится почти наверное?
сходится почти наверное?
0
Пусть![math]() . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов ![math]() функцию
функцию ![math]() , где
, где ![math]() . Пусть
. Пусть ![math]() обозначает число элементов множества
обозначает число элементов множества ![math]() , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств ![math]() , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно![math]() при
при ![math]() ?
?
 . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов  функцию
функцию  , где
, где  . Пусть
. Пусть  обозначает число элементов множества
обозначает число элементов множества  , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств  , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно при
при  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Как у дерева соотносятся число вершин и число ребер?
(1) число ребер и число вершин равны
(2) число ребер на 1 больше числа вершин
(3) число ребер на 1 меньше числа вершин
(4) число ребер на 2 меньше числа вершин
(5) число ребер на 2 больше числа вершин
Сколько существует разложений натурального числа 11 в виде упорядоченной суммы натуральных слагаемых?
1024
Найдите радиус сходимости ряда ![math]() , и выберите какие из перечисленных утверждений являются верными?
, и выберите какие из перечисленных утверждений являются верными?
 , и выберите какие из перечисленных утверждений являются верными?
, и выберите какие из перечисленных утверждений являются верными?
(1) ![math]() принадлежит радиусу сходимости
принадлежит радиусу сходимости
 принадлежит радиусу сходимости
принадлежит радиусу сходимости
(2) ![math]() принадлежит радиусу сходимости
принадлежит радиусу сходимости
 принадлежит радиусу сходимости
принадлежит радиусу сходимости
(3) ![math]() принадлежит радиусу сходимости
принадлежит радиусу сходимости
 принадлежит радиусу сходимости
принадлежит радиусу сходимости
(4) ![math]() принадлежит радиусу сходимости
принадлежит радиусу сходимости
 принадлежит радиусу сходимости
принадлежит радиусу сходимости Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.Хроматическое число графа -
– множество ребер.Хроматическое число графа -
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.Хроматическое число графа -
– множество ребер.Хроматическое число графа -
(1) минимальное число цветов, в которые можно покрасить вершины, так чтобы любые две вершины, соединенные ребром были покрашены в разные цвета
(2) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() принадлежит
принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  принадлежит
принадлежит 
(3) мощность множества ![math]() называется … если для любых
называется … если для любых ![math]() принадлежащих
принадлежащих ![math]() пара
пара ![math]() не принадлежит
не принадлежит ![math]()
 называется … если для любых
называется … если для любых  принадлежащих
принадлежащих  пара
пара  не принадлежит
не принадлежит 
Определите все элементарные исходы, которые при бросании монеты образуют событие, что выпало нечетное число очков.
(1) выпало 1 очко
(2) выпало 2 очка
(3) выпало 3 очка
(4) выпало 4 очка
(5) выпало 5 очков
(6) выпало 6 очков
Во сколько раз оценка для диагональных чисел Рамсея, полученная с помощью локальной леммы Ловаса лучше, чем при использовании только схемы Бернулли?
2
Какая формула определяет количество размещений из ![math]() элементов по
элементов по ![math]() без повторений?
без повторений?
 элементов по
элементов по  без повторений?
без повторений?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Что означает запись ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из ![math]() вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью ![math]() , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от ![math]() . Пусть случайная величина
. Пусть случайная величина ![math]() - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если ![math]() , то чему ассимптотически равна величина
, то чему ассимптотически равна величина ![math]() ?
?
 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Пусть случайная величина
. Пусть случайная величина  - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если  , то чему ассимптотически равна величина
, то чему ассимптотически равна величина  ?
?
0
Рассмотрим пару ![math]() , где
, где ![math]() - любое множество,
- любое множество, ![math]() - совокупность подмножеств в
- совокупность подмножеств в ![math]() . Пусть
. Пусть ![math]() конечное множество, а любое
конечное множество, а любое ![math]() имеет мощность равную
имеет мощность равную ![math]() , что в таком случае представляет собой пара
, что в таком случае представляет собой пара ![math]() ?
?
 , где
, где  - любое множество,
- любое множество,  - совокупность подмножеств в
- совокупность подмножеств в  . Пусть
. Пусть  конечное множество, а любое
конечное множество, а любое  имеет мощность равную
имеет мощность равную  , что в таком случае представляет собой пара
, что в таком случае представляет собой пара  ?
?
(1) однородный гиперграф
(2) граф
(3) ранжированное пространство
(4) топологическое пространство
Пусть задано частично упорядоченное множество (ЧУМ) ![math]() , и для каждого элемента
, и для каждого элемента ![math]() найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса ![math]() на ЧУМ
на ЧУМ ![math]() , если
, если ![math]() ?
?
 , и для каждого элемента
, и для каждого элемента  найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса
найдется только конечное число элементов, предшествующих ему. Чему равна функция Мёбиуса  на ЧУМ
на ЧУМ  , если
, если  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно ![math]() - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на ![math]() вершинах?
вершинах?
 - количество различных (как графы с занумерованными вершинами) деревьев на
- количество различных (как графы с занумерованными вершинами) деревьев на  вершинах?
вершинах?
16
Сколько существует разложений натурального числа 11 в виде упорядоченной суммы натуральных слагаемых длины ровно 5?
210
Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть имеется простой граф ![math]() ,у которого
,у которого ![math]() – множество вершин и
– множество вершин и ![math]() – множество ребер.
– множество ребер.![math]() хроматическое число графа и
хроматическое число графа и ![math]() число независимости графа. Какое утверждение является верным?
число независимости графа. Какое утверждение является верным?
 ,у которого
,у которого  – множество вершин и
– множество вершин и  – множество ребер.
– множество ребер. хроматическое число графа и
хроматическое число графа и  число независимости графа. Какое утверждение является верным?
число независимости графа. Какое утверждение является верным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Числом Рамсея ![math]() называется минимальное число
называется минимальное число ![math]() такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа ![math]() в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф ![math]() , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф ![math]() , у которого все ребра синие. Чему равен
, у которого все ребра синие. Чему равен ![math]() ?
?
 называется минимальное число
называется минимальное число  такое, что при любой раскраске полного графа
такое, что при любой раскраске полного графа  в два цвета - красный и синий, либо существует подграф
в два цвета - красный и синий, либо существует подграф  , у которого все ребра красные, либо существует подграф
, у которого все ребра красные, либо существует подграф  , у которого все ребра синие. Чему равен
, у которого все ребра синие. Чему равен  ?
?
5
Рассмотрим 30 шестиэлементных множеств ![math]() , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие ![math]() состоит в том, что
состоит в том, что ![math]() множество одноцветно. Чему равна
множество одноцветно. Чему равна ![math]() ?
?
 , зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие
, зафиксированных в 50 элементном множестве. Рассмотрим случайную раскраску в два цвета на 50 элементном множестве. Пусть событие  состоит в том, что
состоит в том, что  множество одноцветно. Чему равна
множество одноцветно. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равен биномиальный коэффициент перед выражением ![math]() при разложении
при разложении ![math]() ?
?
 при разложении
при разложении  ?
?
84
Что означает запись ![math]() ?
?
 ?
?
(1)
(2)
(3)
(4) ![math]()

Как можно оценить величину ![math]() , если известно, что
, если известно, что ![math]() независимы в совокупности?
независимы в совокупности?
 , если известно, что
, если известно, что  независимы в совокупности?
независимы в совокупности?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим ранжированное пространство ![math]() , где
, где ![math]() - множество всех закрытых полупространств в
- множество всех закрытых полупространств в ![math]() . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для ![math]() ?
?
 , где
, где  - множество всех закрытых полупространств в
- множество всех закрытых полупространств в  . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для  ?
?
3
Пусть отношение «… делитель…» определяет частичный порядок на множестве ![math]() .Сколько элементов является непосредственными предшественниками элемента, равного 6?
.Сколько элементов является непосредственными предшественниками элемента, равного 6?
 .Сколько элементов является непосредственными предшественниками элемента, равного 6?
.Сколько элементов является непосредственными предшественниками элемента, равного 6?
2
На рисунке представлено дерево. Сколько символов содержит код Прюфера, соответствующий данному дереву.
![files]()

4
Сколько существует диаграмм Юнга произвольного веса, но имеющих не более 6 строк и 4 столбцов?
209
Чему равен одиннадцатый член последовательности, если![math]() ?
?
 ?
?
89
Рассмотрим множество ![math]() - множество всех графов на
- множество всех графов на ![math]() вершинах. Чему равно отношение количества графов
вершинах. Чему равно отношение количества графов ![math]() , для которых кликовое число
, для которых кликовое число ![math]() больше
больше ![math]() к мощности множества
к мощности множества ![math]() если
если ![math]()
 - множество всех графов на
- множество всех графов на  вершинах. Чему равно отношение количества графов
вершинах. Чему равно отношение количества графов  , для которых кликовое число
, для которых кликовое число  больше
больше  к мощности множества
к мощности множества  если
если 
0
Сколько существует способов, покрасить полный граф ![math]() в два цвета - красный и синий?
в два цвета - красный и синий?
 в два цвета - красный и синий?
в два цвета - красный и синий?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() .Пусть
.Пусть ![math]()
![math]() -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем ![math]() множествам
множествам ![math]() , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного ![math]() -элементного подмножества. Пусть событие
-элементного подмножества. Пусть событие ![math]() состоит в том, что
состоит в том, что ![math]() множество одноцветно. Чему равна вероятность
множество одноцветно. Чему равна вероятность ![math]() ?
?
 .Пусть
.Пусть 
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем  множествам
множествам  , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного  -элементного подмножества. Пусть событие
-элементного подмножества. Пусть событие  состоит в том, что
состоит в том, что  множество одноцветно. Чему равна вероятность
множество одноцветно. Чему равна вероятность  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколькими способами можно переставить буквы в слове «КАВКАЗ» так, чтобы получилось новое слово (возможно бессмысленное)?
180
Чему равно математическое ожидание для ![math]() ?
?
 ?
?
2
Какой тип сходимости фигурирует в законе больших чисел в классической формулировке?
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Рассмотрим ранжированное пространство ![math]() , где
, где ![math]() - множество всех закрытых полупространств в
- множество всех закрытых полупространств в ![math]() . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для ![math]() ?
?
 , где
, где  - множество всех закрытых полупространств в
- множество всех закрытых полупространств в  . Чему равна размерность Вапника-Червоненкиса для
. Чему равна размерность Вапника-Червоненкиса для  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Журнал А читают 70% студентов, журнал В – 40% студентов, журнал С – 50% студентов; 30% студентов читают журналы А и В, 40% - журналы А и С, 20% - журналы В и С, 10% - журналы А, В и С. Чему равна ![math]() ?
?
 ?
?
80
Что допускается в унициклическом графе?
(1) кратные ребра
(2) один цикл
(3) циклы
(4) ориентация ребер
Какой знак можно поставить между числом упорядоченных разбиений числа ![math]() и числом неупорядоченных разбиений числа
и числом неупорядоченных разбиений числа ![math]() ?
?
 и числом неупорядоченных разбиений числа
и числом неупорядоченных разбиений числа  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему равен пятый член последовательности числе Фибоначчи?
5
Что является Кнезеровским графом ![math]()

(1) граф Эйлера
(2) паросочетание
(3) полный граф на ![math]() вершинах
вершинах
 вершинах
вершинах
(4) граф Петерсона
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Событие
целиком красная. Событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя.Что является описанием дополнения к событию
целиком синяя.Что является описанием дополнения к событию ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Событие
целиком красная. Событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя.Что является описанием дополнения к событию
целиком синяя.Что является описанием дополнения к событию  ?
?
(1) существует раскраска ребер полного графа ![math]() , при которой нет ни одной красной клики
, при которой нет ни одной красной клики ![math]() и ни одной синей клики
и ни одной синей клики ![math]()
 , при которой нет ни одной красной клики
, при которой нет ни одной красной клики  и ни одной синей клики
и ни одной синей клики 
(2) существует раскраска ребер полного графа ![math]() , при которой есть одна красная клика
, при которой есть одна красная клика ![math]() и одна синяя клика
и одна синяя клика ![math]()
 , при которой есть одна красная клика
, при которой есть одна красная клика  и одна синяя клика
и одна синяя клика 
(3) существует раскраска ребер полного графа ![math]() , при которой есть хотя бы одна красная клика
, при которой есть хотя бы одна красная клика ![math]() или хотя бы одна синяя клика
или хотя бы одна синяя клика ![math]()
 , при которой есть хотя бы одна красная клика
, при которой есть хотя бы одна красная клика  или хотя бы одна синяя клика
или хотя бы одна синяя клика 
 - события. Пусть
- события. Пусть  произвольный орграф зависимостей. И существуют
произвольный орграф зависимостей. И существуют  , что выполняется
, что выполняется  . Что верно относительно
. Что верно относительно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно выражение ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна дисперсия для ![math]() ?
?
 ?
?
4
Если для последовательности случайных величин ![math]() при
при ![math]() выполняется условие
выполняется условие ![math]() в любой
в любой ![math]() - точки непрерывности
- точки непрерывности ![math]() , то говорят, что
, то говорят, что ![math]() сходится к
сходится к ![math]() ...
...
 при
при  выполняется условие
выполняется условие  в любой
в любой  - точки непрерывности
- точки непрерывности  , то говорят, что
, то говорят, что  сходится к
сходится к  ...
...
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Пусть ![math]() , имеется
, имеется ![math]() , причем
, причем ![math]() и
и ![math]() существует
существует ![math]() , которое является
, которое является ![math]() -сетью. От чего зависит мощность
-сетью. От чего зависит мощность ![math]() ?
?
 , имеется
, имеется  , причем
, причем  и
и  существует
существует  , которое является
, которое является  -сетью. От чего зависит мощность
-сетью. От чего зависит мощность  ?
?
(1) от ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

При каком ![math]() достигается максимальное значение величин
достигается максимальное значение величин ![math]() , если
, если ![math]() нечетное число из интервала
нечетное число из интервала ![math]() ?
?
 достигается максимальное значение величин
достигается максимальное значение величин  , если
, если  нечетное число из интервала
нечетное число из интервала  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой граф соответствует коду Прюфера 441666?
(1) ![files]()

(2) ![files]()

(3) ![files]()

Выберите базу рекуррентной формулы количества разбиений числа ![math]() на слагаемые, не превышающие
на слагаемые, не превышающие ![math]() .
.
 на слагаемые, не превышающие
на слагаемые, не превышающие  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

С использованием ![math]() - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция ![math]() .Что верно относительно функции
.Что верно относительно функции ![math]() ?
?
 - чисел Фибоначчи составлена производящая функция
- чисел Фибоначчи составлена производящая функция  .Что верно относительно функции
.Что верно относительно функции  ?
?
(1) g(x)=\frac{x} {1+x+x^2}
(2) g(x)=\frac{x} {1+x-x^2}
(3) g(x)=\frac{x} {1-x+x^2}
(4) g(x)=\frac{x} {1-x-x^2}
Чему равняется кликовое число ![math]() ?
?
 ?
?
(1) 1
(2) ![math]()

(3) ![math]()

Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная. Чему равна вероятность события
целиком красная. Чему равна вероятность события ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Чему равна вероятность события
целиком красная. Чему равна вероятность события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Рассмотрим случайную раскраску полного графа ![math]() на
на ![math]() вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть ![math]() -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и ![math]() - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события ![math]() , где
, где ![math]() -состоит в том, что
-состоит в том, что ![math]() -ый треугольник целиком красный и
-ый треугольник целиком красный и ![math]() -состоит в том, что
-состоит в том, что ![math]() -ая клика размера
-ая клика размера ![math]() целиком синяя. Чему равна
целиком синяя. Чему равна ![math]() ?
?
 на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события  , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и  -состоит в том, что
-состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Чему равна
целиком синяя. Чему равна  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() – последовательность из 0 и 1 длины
– последовательность из 0 и 1 длины ![math]() .Из данного множества выбрали множество
.Из данного множества выбрали множество ![math]() , которое содержит последовательности с ровно
, которое содержит последовательности с ровно ![math]() единицами. Найдите мощность
единицами. Найдите мощность ![math]() .
.
 – последовательность из 0 и 1 длины
– последовательность из 0 и 1 длины  .Из данного множества выбрали множество
.Из данного множества выбрали множество  , которое содержит последовательности с ровно
, которое содержит последовательности с ровно  единицами. Найдите мощность
единицами. Найдите мощность  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание ![math]() ?
?
 ?
?
3
Пусть ![math]() - последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно
- последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно ![math]() . С каким типом сходимости
. С каким типом сходимости ![math]() сходится к
сходится к ![math]() при
при ![math]() ?
?
 - последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно
- последовательность независимых в совокупности и одинакового распределенных случайных величин, для которых математическое ожидание конечно  . С каким типом сходимости
. С каким типом сходимости  сходится к
сходится к  при
при  ?
?
(1) по распределению
(2) по вероятности
(3) в среднем
(4) почти наверное
Пусть ![math]() .Чем ограничена
.Чем ограничена ![math]()
 .Чем ограничена
.Чем ограничена 
(1) ограничена снизу ![math]()

(2) ограничена сверху ![math]()

(3) ограничена снизу ![math]()

(4) ограничена сверху ![math]()

Чему равна асимптотическая оценка ![math]() согласно формуле Стирлинга?
согласно формуле Стирлинга?
 согласно формуле Стирлинга?
согласно формуле Стирлинга?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна асимптотическая оценка выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно ![math]() в рекуррентной формуле количества разбиений числа
в рекуррентной формуле количества разбиений числа ![math]() на
на ![math]() слагаемых.
слагаемых.
 в рекуррентной формуле количества разбиений числа
в рекуррентной формуле количества разбиений числа  на
на  слагаемых.
слагаемых.
0
С использованием ![math]() - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция ![math]() .Что верно относительно функции
.Что верно относительно функции ![math]() ?
?
 - чисел Каталана составлена производящая функция
- чисел Каталана составлена производящая функция  .Что верно относительно функции
.Что верно относительно функции  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно число независимости Кнезеровского графа ![math]() ?
?
 ?
?
4
Рассмотрим все возможные способы покрасить полный граф ![math]() в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя. Чему равно
целиком синяя. Чему равно ![math]() ?
?
 в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя. Чему равно
целиком синяя. Чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим случайную раскраску полного графа ![math]() на
на ![math]() вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть ![math]() -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и ![math]() - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события ![math]() , где
, где ![math]() состоит в том, что
состоит в том, что ![math]() -ый треугольник целиком красный и
-ый треугольник целиком красный и ![math]() состоит в том, что
состоит в том, что ![math]() -ая клика размера
-ая клика размера ![math]() целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события ![math]() построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины ![math]() орграфа зависимостей в вершины
орграфа зависимостей в вершины ![math]() ?
?
 на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события  , где
, где  состоит в том, что
состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и  состоит в том, что
состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события  построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины  орграфа зависимостей в вершины
орграфа зависимостей в вершины  ?
?
(1) ![math]()

(2) C_t^2![math]()

(3) ![math]()

Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна дисперсия ![math]() , если известно
, если известно ![math]() ?
?
 , если известно
, если известно  ?
?
27
Какой тип сходимости фигурирует в центральной предельной теореме?
(1) сходимость почти наверное
(2) сходимость по вероятности
(3) сходимость по распределению
(4) сходимость в среднем
Пусть ![math]() .Пусть
.Пусть ![math]() . Тогда
. Тогда ![math]() ограничена ...
ограничена ...
 .Пусть
.Пусть  . Тогда
. Тогда  ограничена ...
ограничена ...
(1) сверху ![math]()

(2) снизу ![math]()

(3) сверху ![math]()

(4) снизу ![math]()

Выберите наименьшее выражение из перечисленных.
(1) ![math]()

(2) ![math]()

(3) Число перестановок без повторений из ![math]() элементов
элементов
 элементов
элементов В формуле оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах
вершинах ![math]() выражение
выражение ![math]() показывает...
показывает...
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах  выражение
выражение  показывает...
показывает...
(1) число способов построить цикл на выбранных вершинах
(2) число способов зафиксировать вершины для цикла
(3) число способов зафиксировать цикл
(4) число различных (как графы с занумерованными вершинами) лесов с ![math]() деревьями с общим количеством вершин
деревьями с общим количеством вершин ![math]() , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …, ![math]() -ое дерево содержит вершину
-ое дерево содержит вершину ![math]()
 деревьями с общим количеством вершин
деревьями с общим количеством вершин  , такое, что первое дерево содержит вершину 1, второе – вершину 2, …,
, такое, что первое дерево содержит вершину 1, второе – вершину 2, …,  -ое дерево содержит вершину
-ое дерево содержит вершину 
Пусть ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и ![math]() - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа ![math]() , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность ![math]() и
и ![math]() , если
, если ![math]() ?
?
 - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых четное количество слагаемых, и
, в которых четное количество слагаемых, и  - количество различных неупорядоченных разбиений числа
- количество различных неупорядоченных разбиений числа  , в которых нечетное количество слагаемых. Чему равна разность
, в которых нечетное количество слагаемых. Чему равна разность  и
и  , если
, если  ?
?
1
Используя операции с формальными степенными рядами, определите чему равен коэффициент при ![math]() при разложении
при разложении ![math]() в формальный степенной ряд.
в формальный степенной ряд.
 при разложении
при разложении  в формальный степенной ряд.
в формальный степенной ряд.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно число независимости Кнезеровского графа ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() , то выражение
, то выражение ![math]() будет ...
будет ...
 , то выражение
, то выражение  будет ...
будет ...
(1) неположительным
(2) неотрицательным
(3) положительным
(4) отрицательным
Для событий ![math]() составлено равенство
составлено равенство ![math]() Каким должен быть последний сомножитель, чтобы это выражение было правильным?
Каким должен быть последний сомножитель, чтобы это выражение было правильным?
 составлено равенство
составлено равенство  Каким должен быть последний сомножитель, чтобы это выражение было правильным?
Каким должен быть последний сомножитель, чтобы это выражение было правильным?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Имеется множество объектов ![math]() , из которого выбираются сочетания по
, из которого выбираются сочетания по ![math]() элементов. Из множества всех возможных сочетаний выбрали подмножество
элементов. Из множества всех возможных сочетаний выбрали подмножество ![math]() , в котором ровно
, в котором ровно ![math]() элементов принадлежат
элементов принадлежат ![math]() .Найдите мощность
.Найдите мощность ![math]() .
.
 , из которого выбираются сочетания по
, из которого выбираются сочетания по  элементов. Из множества всех возможных сочетаний выбрали подмножество
элементов. Из множества всех возможных сочетаний выбрали подмножество  , в котором ровно
, в котором ровно  элементов принадлежат
элементов принадлежат  .Найдите мощность
.Найдите мощность  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно математическое ожидание>x ![math]() ?
?
 ?
?
5
Пусть ![math]() . Чему равно
. Чему равно ![math]() ?
?
 . Чему равно
. Чему равно  ?
?
0
Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Что является верным относительно
. Что является верным относительно ![math]() и
и ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Что является верным относительно
. Что является верным относительно  и
и  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите наименьшее выражение из перечисленных.
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какова точная оценка количества унициклических графов ![math]() ?
?
 ?
?
(1) ![math]() вершинах
вершинах ![math]()
 вершинах
вершинах 
(2) ![math]() вершинах
вершинах ![math]()
 вершинах
вершинах 
(3) ![math]() вершинах
вершинах ![math]()
 вершинах
вершинах 
(4) ![math]() вершинах
вершинах ![math]()
 вершинах
вершинах 
Пусть ![math]() и
и ![math]() . Чему равен коэффициент перед
. Чему равен коэффициент перед ![math]() формального степенного ряда
формального степенного ряда ![math]() ?
?
 и
и  . Чему равен коэффициент перед
. Чему равен коэффициент перед  формального степенного ряда
формального степенного ряда  ?
?
0
Чему равен шестой член последовательности чисел Каталана?
132
Чему равно число независимости Кнезеровского графа ![math]() , если
, если ![math]() ?
?
 , если
, если  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой знак правильно поставить между ![math]() и
и ![math]() ?
?
 и
и  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему согласно теореме Муавра-Лапласа равна вероятность того, что число успехов по схеме Бернулли, центрированное ![math]() и нормированное
и нормированное ![math]() находится в пределах от
находится в пределах от ![math]() до
до ![math]() , если
, если ![math]() - число испытаний,
- число испытаний, ![math]() - вероятность успеха в одном испытании,
- вероятность успеха в одном испытании, ![math]() - вероятность неудачи в одном испытании?
- вероятность неудачи в одном испытании?
 и нормированное
и нормированное  находится в пределах от
находится в пределах от  до
до  , если
, если  - число испытаний,
- число испытаний,  - вероятность успеха в одном испытании,
- вероятность успеха в одном испытании, 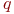 - вероятность неудачи в одном испытании?
- вероятность неудачи в одном испытании?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно значение знакопеременного выражения ![math]() , если
, если ![math]() ?
?
 , если
, если  ?
?
(1) 0
(2) 1
(3) -1
(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной ![math]() проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью ![math]() не проводим. Пусть
не проводим. Пусть ![math]() - число треугольников в случайном графе. чему равно
- число треугольников в случайном графе. чему равно ![math]() ?
?
 фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной  проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью  не проводим. Пусть
не проводим. Пусть  - число треугольников в случайном графе. чему равно
- число треугольников в случайном графе. чему равно  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() - характеристическая функция. Чему равно ее разложение в ряд Тейлора?
- характеристическая функция. Чему равно ее разложение в ряд Тейлора?
 - характеристическая функция. Чему равно ее разложение в ряд Тейлора?
- характеристическая функция. Чему равно ее разложение в ряд Тейлора?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , где
, где ![math]() по схеме выбора с возращением
по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Если известно
. Если известно ![math]() , что является верным относительно
, что является верным относительно ![math]() и
и ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , где
, где  по схеме выбора с возращением
по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Если известно
. Если известно  , что является верным относительно
, что является верным относительно  и
и  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие функции могут быть записаны в виде ![math]() , где постоянная
, где постоянная ![math]() ?
?
 , где постоянная
, где постоянная  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

При построении асимптотической оценки количества различных (как графы с занумерованными вершинами) унициклических графов с ![math]() вершинами и циклом, построенным на
вершинами и циклом, построенным на ![math]() вершинах, величина
вершинах, величина ![math]() заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых ![math]() .При указанном интервале суммирования для
.При указанном интервале суммирования для ![math]() , что является нижней оценкой величины
, что является нижней оценкой величины ![math]() ?
?
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах, величина
вершинах, величина  заменяется на сумму двух слагаемых
заменяется на сумму двух слагаемых  .При указанном интервале суммирования для
.При указанном интервале суммирования для  , что является нижней оценкой величины
, что является нижней оценкой величины  ?
?
(1) ![math]()

(2) ![math]()

(3) 0
(4) 1
Пусть ![math]() и
и ![math]() . Чему равен коэффициент перед
. Чему равен коэффициент перед ![math]() формального степенного ряда
формального степенного ряда ![math]() ?
?
 и
и  . Чему равен коэффициент перед
. Чему равен коэффициент перед  формального степенного ряда
формального степенного ряда  ?
?
0
Сколько решений имеет cоотношение на элементы бесконечной последовательности ![math]() удовлетворяющее условию
удовлетворяющее условию ![math]() , где постоянные величины
, где постоянные величины ![math]() ?
?
 удовлетворяющее условию
удовлетворяющее условию  , где постоянные величины
, где постоянные величины  ?
?
(1) 0
(2) ![math]()

(3) 1
(4) ![math]()

Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() . Рассмотрим
. Рассмотрим ![math]() - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа ![math]() . Что верно относительно мощности
. Что верно относительно мощности ![math]() ?
?
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определим случайную раскраску так: с вероятностью ![math]() красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью ![math]() красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком синяя.Cобытие
целиком синяя.Cобытие ![math]() состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске ![math]() -ая по счету клика
-ая по счету клика ![math]() в графе
в графе ![math]() целиком красная.Чему равняется вероятность события
целиком красная.Чему равняется вероятность события ![math]() ?
?
 красим очередное ребро в красный цвет, с вероятностью
красим очередное ребро в красный цвет, с вероятностью  красим очередное ребро в синий цвет.Пусть событие
красим очередное ребро в синий цвет.Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком синяя.Cобытие
целиком синяя.Cобытие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная.Чему равняется вероятность события
целиком красная.Чему равняется вероятность события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Для событий ![math]() для любого
для любого ![math]() и любого
и любого ![math]() , и если
, и если ![math]() выполняется равенство
выполняется равенство ![math]() .Чему равна
.Чему равна ![math]() если
если ![math]() ?
?
 для любого
для любого  и любого
и любого  , и если
, и если  выполняется равенство
выполняется равенство  .Чему равна
.Чему равна  если
если  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна функция Мебиуса ![math]() , если
, если ![math]() несвободно от квадратов (то есть делится на квадрат простого числа)?
несвободно от квадратов (то есть делится на квадрат простого числа)?
 , если
, если  несвободно от квадратов (то есть делится на квадрат простого числа)?
несвободно от квадратов (то есть делится на квадрат простого числа)?
0
Пусть дана последовательность случайных величин ![math]() . Какое условие на
. Какое условие на ![math]() -
- ![math]() -ые факториальные моменты должно выполняться, чтобы
-ые факториальные моменты должно выполняться, чтобы ![math]() ?
?
 . Какое условие на
. Какое условие на  -
-  -ые факториальные моменты должно выполняться, чтобы
-ые факториальные моменты должно выполняться, чтобы  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Имеется бесконечная последовательность одинаково распределенных и независимых случайных величин ![math]() . Обозначим
. Обозначим ![math]() . Чему равна характеристическая функция для
. Чему равна характеристическая функция для ![math]() ?
?
 . Обозначим
. Обозначим  . Чему равна характеристическая функция для
. Чему равна характеристическая функция для  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Укажите все выражения равные ![math]() , где
, где ![math]() ?
?
 , где
, где  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равно значение выражения ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Сколько решений имеет характеристическое уравнение для рекуррентного соотношения ![math]() ?
?
 ?
?
2
Имеется множество натуральных чисел от 1 до ![math]() . И определены следуюшие подмножества
. И определены следуюшие подмножества ![math]() ,
, ![math]() ,...,
,...,![math]() ,...,
,..., ![math]() . Обозначим
. Обозначим ![math]() .Среди множеств
.Среди множеств ![math]() и
и ![math]() выберите множество, с котором не пересекается
выберите множество, с котором не пересекается ![math]() .
.
 . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств  и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность пересечения события ![math]() и события
и события ![math]() ?
?
 и события
и события  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна вероятность, что два человека встретятся, если они договорились, что каждый приходит в любое время в течении определенного часа, и если другого нет, ждет десять минут, потом уходит? В ответ ввести четыре знака после запятой.
0,3055
Согласно формуле обращения Мебиуса для арифметических функций ![math]() и
и ![math]() верно
верно ![math]() тогда и только тогда, когда
тогда и только тогда, когда ![math]() равна … (укажите все возможные ответы).
равна … (укажите все возможные ответы).
 и
и  верно
верно  тогда и только тогда, когда
тогда и только тогда, когда  равна … (укажите все возможные ответы).
равна … (укажите все возможные ответы).
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассмотрим случайный граф на ![math]() фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной ![math]() проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью ![math]() не проводим. Пусть
не проводим. Пусть ![math]() - число изолированных ребер в графе
- число изолированных ребер в графе ![math]() Чему равен второй факториальный момент
Чему равен второй факториальный момент ![math]() ?
?
 фиксированных вершинах, где с вероятностью равной
фиксированных вершинах, где с вероятностью равной  проводим ребро, соответственно, с вероятностью
проводим ребро, соответственно, с вероятностью  не проводим. Пусть
не проводим. Пусть  - число изолированных ребер в графе
- число изолированных ребер в графе  Чему равен второй факториальный момент
Чему равен второй факториальный момент  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Известно, что последовательность случайных величн сходится по распределению к некоторой константе, то с каким еще типом сходимости эта же случайная величина сходится к константе
(1) по распределению
(2) по вероятности
(3) почти наверное
(4) в среднем
Пусть ![math]() . Из множества
. Из множества ![math]() выбираем случайные подмножества
выбираем случайные подмножества ![math]() и
и ![math]() из
из ![math]() , по схеме выбора с возращением
, по схеме выбора с возращением ![math]() . Пусть определены события
. Пусть определены события ![math]() и
и ![math]() . Какое
. Какое ![math]() требуется взять, чтобы
требуется взять, чтобы ![math]() ?
?
 . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , по схеме выбора с возращением
, по схеме выбора с возращением  . Пусть определены события
. Пусть определены события  и
и  . Какое
. Какое  требуется взять, чтобы
требуется взять, чтобы  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для эквивалентных асимптотически функций ![math]() и
и ![math]() выполняется равенство ...
выполняется равенство ...
 и
и  выполняется равенство ...
выполняется равенство ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определите число различных (как графы с занумерованными вершинами) лесов с 2 деревьями с общим количеством вершин 6, такое, что первое дерево содержит вершину 1, второе – вершину 2.
216
Найдите формальный степенной ряд ![math]() , удовлетворяющий равенству
, удовлетворяющий равенству ![math]() .
.
 , удовлетворяющий равенству
, удовлетворяющий равенству  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найдите наименьшее по модулю решение характеристическое уравнение для рекуррентного соотношения ![math]() .
.
 .
.
1
Рассмотрим Кнезеровский граф ![math]() . Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет
. Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет ![math]() все вершины, которые содержат
все вершины, которые содержат ![math]() . Сколько еще потребуется цветов, чтобы раскрасить граф таким образом, как это требуется для определения хроматического числа графа?
. Сколько еще потребуется цветов, чтобы раскрасить граф таким образом, как это требуется для определения хроматического числа графа?
 . Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет
. Покрасим в цвет 1 все вершины, которые содержат 1; в цвет 2 все вершины, которые содержат 2, ..., в цвет  все вершины, которые содержат
все вершины, которые содержат  . Сколько еще потребуется цветов, чтобы раскрасить граф таким образом, как это требуется для определения хроматического числа графа?
. Сколько еще потребуется цветов, чтобы раскрасить граф таким образом, как это требуется для определения хроматического числа графа?
1
В двух урнах находится соответственно 4 и 5 белых и 6 и 3 черных шаров. Из каждой урны наудачу извлекается один шар, а затем из этих двух наудачу берется один. Какова вероятность, что это будет черный шар? Ответ округлить до сотых.
0,49
К автобусной остановке через каждые четыре минуты подходит автобус линии А и через каждые шесть минут — автобус линии В. Интервал времени между моментами прихода автобуса линии А и ближайшего следующего автобуса линии В равновозможен в пределах от нуля до четырех минут. Определить вероятность того, что автобус какой-либо линии подойдет в течение двух минут. Ответ округлить до сотых.
0,67