Главная /
Математика /
Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе рассмотрены основные понятия и принципы экономико-математического моделирования, представлены классические и неоклассические модели экономических процессов, и показаны технологии их реализации сервисами MathCAD.
Все ответы: В курсе рассмотрены основные понятия и принципы экономико-математического моделирования, представлены классические и неоклассические модели экономических процессов, и показаны технологии их реализации сервисами MathCAD.
Смотрите также:
Функция ![math]() имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
 имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
(1) 0
(2) -1
(3) 1
(4) не существует
Если сложные проценты начисляются несколько раз в году, то при финансовых расчетах срок финансовой операции:
(1) делится на количество начислений
(2) остается без изменения
(3) умножается на количество начислений
(4) не учитывается в расчетах
Промежуточная продукция в межотраслевом балансе это -
(1) продукция, направляемая вне сферы производственного потребления
(2) продукция, представляющая полуфабрикат основной продукции каждой отрасли
(3) продукция отрасли, поступающая во все отрасли для поддержания производственного процесса
(4) разность конечной и валовой продукции отрасли
Какие методы используются при решении задачи оптимизации?
(1) методы математического программирования
(2) методы математического анализа
(3) методы дифференциальных уравнений
(4) методы математической статистики
Что такое имитационная модель экономического процесса?
(1) закон распределения
(2) программный комплекс (или программа)
(3) система уравнений
(4) функция генерации
Дайте определения нечеткого множества А:
(1) нечеткое множество ![math]() - универсальное множество
- универсальное множество ![math]() , каждый элемент которого имеет определенную степень принадлежности
, каждый элемент которого имеет определенную степень принадлежности
 - универсальное множество
- универсальное множество  , каждый элемент которого имеет определенную степень принадлежности
, каждый элемент которого имеет определенную степень принадлежности
(2) нечеткое множество ![math]() - пара
- пара ![math]() , где
, где ![math]() — универсальное множество,
— универсальное множество, ![math]() — функция, определенная на множестве
— функция, определенная на множестве ![math]() и принимающая значения
и принимающая значения ![math]()
 - пара
- пара  , где
, где  — универсальное множество,
— универсальное множество,  — функция, определенная на множестве
— функция, определенная на множестве  и принимающая значения
и принимающая значения 
(3) нечеткое множество ![math]() - пара
- пара ![math]() , где
, где ![math]() — универсальное множество,
— универсальное множество, ![math]() — функция, определенная на множестве
— функция, определенная на множестве ![math]() и принимающая значения на отрезке
и принимающая значения на отрезке ![math]()
 - пара
- пара  , где
, где  — универсальное множество,
— универсальное множество,  — функция, определенная на множестве
— функция, определенная на множестве  и принимающая значения на отрезке
и принимающая значения на отрезке 
(4) нечеткое множество ![math]() - пара
- пара ![math]() , где
, где ![math]() — универсальное множество,
— универсальное множество, ![math]() — функция, определенная на множестве
— функция, определенная на множестве ![math]() и принимающая два значения: 0 или 1
и принимающая два значения: 0 или 1
 - пара
- пара  , где
, где  — универсальное множество,
— универсальное множество,  — функция, определенная на множестве
— функция, определенная на множестве  и принимающая два значения: 0 или 1
и принимающая два значения: 0 или 1 Экстремальное значение функции ![math]() равно:
равно:
 равно:
равно:
(1) 4
(2) 5
(3) 6
(4) не существует
Выражение ![math]() лежит в основе расчета
лежит в основе расчета
 лежит в основе расчета
лежит в основе расчета
(1) современной стоимости элементарного денежного потока
(2) будущей стоимости элементарного денежного потока
(3) дисконтированной стоимости денежного потока
(4) текущей стоимости финансовой ренты
Уравнение межотраслевого баланса имеет вид:
(1)
(E - A)X =Y
(2)
(E - A)Y =X
(3)
X = AX+ Y
(4)
Y = AY+ X Факторы, порождающие ограничения в оптимизационных моделях экономических задач:
(1) стремление получить максимальную прибыль;
(2) использование ресурсов, запасы которых ограничены;
(3) условия на соотношения между группами управляемых переменных,
(4) обеспечение минимальных затрат
Цель имитационного моделирования методом Монте-Карло -
(1) определение оптимальных значений исследуемых показателей,
(2) построение вероятностных законов распределения исследуемых показателей.
(3) определение экстремальных значений исследуемых показателей,
(4) определение стохастических значений исследуемых показателей,
Характеристическая функция "обычного" множества ![math]() это -
это -
 это -
это -
(1) любая функция, заданная на множестве ![math]() и принимающая значения 0 или 1
и принимающая значения 0 или 1
 и принимающая значения 0 или 1
и принимающая значения 0 или 1
(2) функция, заданная на универсальном множестве ![math]() и принимающая значение 1, если элемент принадлежит данному множеству
и принимающая значение 1, если элемент принадлежит данному множеству ![math]() и значение 0, если не принадлежит
и значение 0, если не принадлежит
 и принимающая значение 1, если элемент принадлежит данному множеству
и принимающая значение 1, если элемент принадлежит данному множеству  и значение 0, если не принадлежит
и значение 0, если не принадлежит
(3) функция, заданная на универсальном множестве ![math]() и принимающая значения на отрезке
и принимающая значения на отрезке ![math]()
 и принимающая значения на отрезке
и принимающая значения на отрезке 
(4) функция, заданная на универсальном множестве ![math]() и принимающая значения
и принимающая значения ![math]()
 и принимающая значения
и принимающая значения 
Функция ![math]() имеет перегибы при значениях
имеет перегибы при значениях
 имеет перегибы при значениях
имеет перегибы при значениях x, равных:
(1) 0,3
(2) 1,3
(3) 1,7
(4) 2,7
Выражение для наращенной стоимости постоянной финансовой ренты имеет вид:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой смысл имеют элементы матрицы прямых затрат aij:
(1) доля продукции i-й отрасли в затратах на производство единицы продукции j -й отрасли
(2) объем продукции i-й отрасли, расходуемый на производство единицы продукции конечной продукции j-отрасли
(3) часть общего валового продукта , израсходованная на производственные нужды в процессе производства
(4) затраты валового продукта i-й отрасли на воспроизводство единицы конечного продукта j-й отрасли
В качестве целевой функции в экономической оптимизационной задаче выбирается
(1) величина прибыли,
(2) расход ресурсов,
(3) значения управляемых переменных,
(4) показатель, для которого определяется экстремум
Метод Монте-Карло использует законы
(1) теории оптимизации,
(2) теории иерархии,
(3) теории вероятности,
(4) теории аппроксимации
Несущим множеством или носителем нечеткого множества A, определенного на множестве U, называют:
(1) подмножество множества ![math]() , состоящее из элементов, на которых функция принадлежности нечеткого множества
, состоящее из элементов, на которых функция принадлежности нечеткого множества ![math]() принимает значения 0 или 1
принимает значения 0 или 1
 , состоящее из элементов, на которых функция принадлежности нечеткого множества
, состоящее из элементов, на которых функция принадлежности нечеткого множества  принимает значения 0 или 1
принимает значения 0 или 1
(2) подмножество множества ![math]() , состоящее нечеткого множества
, состоящее нечеткого множества ![math]() из элементов, на которых функция принадлежности нечеткого множества
из элементов, на которых функция принадлежности нечеткого множества ![math]()
 , состоящее нечеткого множества
, состоящее нечеткого множества  из элементов, на которых функция принадлежности нечеткого множества
из элементов, на которых функция принадлежности нечеткого множества 
(3) называют множество ![math]()

(4) подмножество множества ![math]() , состоящее из элементов, на которых функция принадлежности нечеткого множества
, состоящее из элементов, на которых функция принадлежности нечеткого множества ![math]()
 , состоящее из элементов, на которых функция принадлежности нечеткого множества
, состоящее из элементов, на которых функция принадлежности нечеткого множества 
Функция
rows(А) определяет:
(1) число столбцов в матрице
А
(2) число строк в матрице
А
(3) индекс последнего элемента в матрице
А
(4) сортировку строк в матрице
А Какой аргумент финансовых функций учитывает разное поступление платежей в течение периода финансовой ренты:
(1) ставка
(2) количество периодов
(3) платеж
(4) тип ренты
Коэффициент прямых затрат труда это:
(1) разность затрат живого труда на производство общего объема продукции и конечной продукции
(2) затраты живого труда на производство единицы общего объема произведенной продукции
(3) затраты живого труда на производство единицы конечной продукции
(4) отношение общего объема произведенной продукции к затратам живого труда на его производство
Пусть на трех складах хранится однотипная продукция ![math]() , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве ![math]() , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей ![math]() . Для выполнения заказа и обеспечения минимальных затрат необходимо:
. Для выполнения заказа и обеспечения минимальных затрат необходимо:
 , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей  . Для выполнения заказа и обеспечения минимальных затрат необходимо:
. Для выполнения заказа и обеспечения минимальных затрат необходимо:
(1) сократить заказ 1 потребителю на 80 ед,
(2) сократить заказ 2 потребителю на 80 ед,
(3) сократить заказ 3 потребителю на 80 ед,,
(4) сократить заказ 1 потребителю на 40 ед. и 2 потребителю на 40 ед.
В результате моделирования Монте-Карло разные прогнозные сценарии создаются за счет:
(1) выбора разных видов распределений входных стохастических переменных,
(2) различных допущений о поведении входных стохастических переменных,
(3) выбора разного алгоритма зависимости исследуемого показателя,
(4) выбора разных параметров заданных распределений.
Точкой перехода нечеткого множества называют:
(1) элемент множества ![math]() , на котором функция принадлежности
, на котором функция принадлежности ![math]()
 , на котором функция принадлежности
, на котором функция принадлежности 
(2) элемент множества ![math]() , на котором функция принадлежности
, на котором функция принадлежности ![math]()
 , на котором функция принадлежности
, на котором функция принадлежности 
(3) элемент множества ![math]() , на котором функция принадлежности
, на котором функция принадлежности ![math]()
 , на котором функция принадлежности
, на котором функция принадлежности 
(4) элемент множества ![math]() , на котором функция принадлежности
, на котором функция принадлежности ![math]()
 , на котором функция принадлежности
, на котором функция принадлежности 
Для системы уравнений ![math]() соотношение между
соотношение между
 соотношение между
соотношение между a,b.d,p, при котором система не имеет решений, имеет вид:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Ссуда в 5000 ед. получена на полтора года под ставку 10% годовых с ежеквартальным начислением. Возвращаемая сумма составит:
(1) 5498 ед.
(2) 5598 ед.
(3) 5698 ед.
(4) 5798 ед.
Если
E – единичная матрица, A-матрица прямых затрат, матрица, B - матрица полных затрат имеет вид:
(1)
B=(E-A)
(2)
B=(E-A)-1
(3)
B=(A-E)-1
(4)
B=( A- E) В транспортной задаче, когда общее количество груза меньше, чем требуется потребителям, вводится:
(1) дополнительный потребитель
(2) дополнительный поставщик
(3) добавляется стоимость транспортировки
(4) уменьшается стоимость транспортировки
Для проведения имитационного эксперимента необходимо провести компьютерную имитацию:
(1) всех показателей,
(2) выходного показателя,
(3) входных стохастических показателей,
(4) детерминированных показателей.
Множеством ![math]() –уровня нечеткого множества
–уровня нечеткого множества ![math]() называется :
называется :
 –уровня нечеткого множества
–уровня нечеткого множества  называется :
называется :
(1) множество всех значений функции принадлежности нечеткого множества, удовлетворяющих неравенству: ![math]()

(2) четкое подмножество, которое состоит из элементов универсального множества ![math]() , для которых выполняется неравенство
, для которых выполняется неравенство ![math]()
 , для которых выполняется неравенство
, для которых выполняется неравенство 
(3) множество всех значений функции принадлежности нечеткого множества, удовлетворяющих неравенству: ![math]()

(4) четкое подмножество, которое состоит из элементов универсального множества ![math]() , для которых выполняется неравенство
, для которых выполняется неравенство ![math]()
 , для которых выполняется неравенство
, для которых выполняется неравенство 
Производная ![math]() для функций, заданных параметрически:
для функций, заданных параметрически: ![math]() , равна:
, равна:
 для функций, заданных параметрически:
для функций, заданных параметрически:  , равна:
, равна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Дисконтирование позволяет:
(1) определить будущее значение денежной суммы по ее текущему значению,
(2) определить современную стоимость денежной суммы по ее будущему значению,
(3) определить срок финансовой операции.
(4) определить доходность финансовой операции.
Конечный продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции ![math]() . Общие затраты труда составят:
. Общие затраты труда составят:
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции  . Общие затраты труда составят:
. Общие затраты труда составят:
(1) 1560
(2) 1570
(3) 1580
(4) 1590
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны ![math]() . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны ![math]() . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей ![math]() . Максимальная оптимальная прибыль (усл. ед.) составит:
. Максимальная оптимальная прибыль (усл. ед.) составит:
 . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны  . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Максимальная оптимальная прибыль (усл. ед.) составит:
. Максимальная оптимальная прибыль (усл. ед.) составит:
(1) 450
(2) 440
(3) 430
(4) 420
Имитационная выборка выходного показателя создается в результате:
(1) компьютерной имитации
(2) расчета по имитируемым параметрам,
(3) задания закона распределения выходного показателя
(4) задания коэффициента корреляции входного и выходного показателя.
Как называется функция принадлежности, описываемая законом
(1) треугольная
(2) трапециевидная
(3) гауссова
(4) Z-образная
Для функции, заданной в виде ![math]() , значение
, значение ![math]() равно:
равно:
 , значение
, значение  равно:
равно:
(1) 7,6
(2) 6,6
(3) 5,6
(4) 4,6
Сумма 2000 ед. вырастет до 8000 ед. при вложении в банк под ставку 10% (с учетом капитализации) за срок:
(1) 12,5 лет
(2) 13,5 лет
(3) 14,5 лет
(4) 15,5 лет
Продуктивность матрицы коэффициентов прямых затрат означает:
(1) все коэффициенты прямых затрат неотрицательны
(2) все коэффициенты прямых затрат ![math]()

(3) при любых значениях конечной продукции уравнение межотраслевого баланса имеет неотрицательные решения (валовая продукция неотрицательна)
(4) коэффициенты полных затрат больше коэффициентов прямых затрат
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый, и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. Каких сотрудников надо привлечь для выполнения всего проекта, чтобы фонд оплаты был минимальным:
(1) 4 инженера, 1 программист и 3 менеджера,
(2) 3 инженера, 1 программист и 4 менеджера.
(3) 3 инженера, 2 программиста и 3 менеджера,
(4) 5 инженеров, 1 программист и 2 менеджера
Частотное распределение выходного показателя имитационной модели в Mathcad строится с использованием функции:
(1)
rnorm( )
(2)
runif( )
(3)
rnd( )
(4)
histogram( )
Выбрать для нечеткого множества ![math]() множество, ближайшее к нечеткому.
множество, ближайшее к нечеткому.
 множество, ближайшее к нечеткому.
множество, ближайшее к нечеткому.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть производительность труда от времени ![math]() , объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
, объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
t характеризуется функцией  , объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
, объем произведенной работы (в усл. ед.) за первый час рабочего дня равен:
(1) 8,2
(2) 7,2
(3) 6,2
(4) 5,2
Выражение ![math]() лежит в основе расчета
лежит в основе расчета
 лежит в основе расчета
лежит в основе расчета
(1) периодического платежа финансовой ренты пренумерандо
(2) периодического платежа финансовой ренты постнумерандо
(3) срока накопления финансовой ренты пренумерандо
(4) срока накопления финансовой ренты постнумерандо
Конечный продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() . Вектор валового продукта равен:
. Вектор валового продукта равен:
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  . Вектор валового продукта равен:
. Вектор валового продукта равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи в "комплектной постановке" (использование только имеющихся ресурсов) в качестве целевой функции выбирается:
(1) прибыль
(2) доля выполнения плана
(3) суммарное количество используемых ресурсов
(4) количество недостающих ресурсов
Для анализа результатов имитационного моделирования методом Монте - Карло для выходного показателя рассчитываются:
(1) +статистические характеристики
(2) экономические характеристики
(3) +вероятностные характеристики
(4) аналитические характеристики
Термин супремум обозначает :
(1) минимальное значение функции принадлежности ![math]() , нечеткого множества А
, нечеткого множества А
 , нечеткого множества А
, нечеткого множества А
(2) максимальное значение функции принадлежности ![math]() , нечеткого множества А
, нечеткого множества А
 , нечеткого множества А
, нечеткого множества А
(3) нулевое значение функции принадлежности ![math]() , нечеткого множества А
, нечеткого множества А
 , нечеткого множества А
, нечеткого множества А
(4) значение функции принадлежности ![math]() , нечеткого множества А
, нечеткого множества А
 , нечеткого множества А
, нечеткого множества А Функция спроса имеет вид ![math]() , функция предложения
, функция предложения ![math]() , где
, где ![math]() и
и ![math]() – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, ![math]() - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
 , функция предложения
, функция предложения  , где
, где 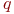 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
(1) 1
(2) 2
(3) 3
(4) 4
Современная стоимость суммы 7000 ед, полученной через 4,5 года после вложения инвестиции, при уровне доходности 12% составит:
(1) 6305 ед.
(2) 6205 ед.
(3) 6105 ед.
(4) 6005 ед.
Валовый продукт ![math]() , матрица межотраслевых поставок
, матрица межотраслевых поставок ![math]() . Конечный продукт равен:
. Конечный продукт равен:
 , матрица межотраслевых поставок
, матрица межотраслевых поставок  . Конечный продукт равен:
. Конечный продукт равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи с добавлением ресурсов - в качестве целевой функции выбирается:
(1) прибыль
(2) суммарное количество добавляемых ресурсов
(3) суммарное количество используемых ресурсов
(4) количество недостающих ресурсов
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов:
1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Стохастические переменные задачи:
(1) доходы по годам
(2) сумма кредита
(3) процентная ставка
(4) расходы
Какие инструменты MathCad можно использовать для построения функции принадлежности нечеткого множества .
(1) встроенные функции категории Statistics (Статистика)
(2) операции с матрицами
(3) функция
if ()
(4) символьное решение уравнений
Спрос на товары первой необходимости выражается функцией Торнквиста ![math]() , где
, где ![math]() - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
(1) 10
(2) 20
(3) 30
(4) 40
Сумма в 20000 ед. , помещена в банк. под ставку 8% годовых с последующим ежегодным пополнением суммами в 5000. ед.. Проценты начисляются раз в год с капитализацией. Сумма к концу 3 года составит:
(1) 38180 ед.
(2) 38280 ед
(3) 38380 ед
(4) 38480 ед
Конечный продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() , затраты живого труда
, затраты живого труда ![math]() , вектор полной трудоемкости
, вектор полной трудоемкости
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда  , вектор полной трудоемкости
, вектор полной трудоемкости T равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны ![math]() . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны ![math]() . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей ![math]() . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
 . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны  . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). При имеющихся ресурсах оптимальный процент выполнения заказа составит:
(1) 26%
(2) 36%
(3) 46%
(4) 56%
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, для оценки эффективности проекта следует определить:
(1) вероятность чистой приведенной стоимости прибыли быть >0
(2) вероятность максимума прибыли
(3) вероятность минимума затрат
(4) оптимальную прибыль
Имеется нечеткое множество ![math]() и обычное множество
и обычное множество ![math]() ближайшее к нечеткому множеству
ближайшее к нечеткому множеству ![math]() , индекс нечеткости по линейной метрике
, индекс нечеткости по линейной метрике ![math]() множества
множества ![math]() определяется по формуле:
определяется по формуле:
 и обычное множество
и обычное множество  ближайшее к нечеткому множеству
ближайшее к нечеткому множеству  , индекс нечеткости по линейной метрике
, индекс нечеткости по линейной метрике  множества
множества  определяется по формуле:
определяется по формуле:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
 имеет экстремум при значении x, равном:
имеет экстремум при значении x, равном:
(1) 0.607
(2) 1.607
(3) 2.607
(4) не существует
Если сложные проценты начисляются несколько раз в году, то при финансовых расчетах годовая процентная ставка:
(1) умножается на количество начислений
(2) остается без изменения
(3) делится на количество начислений
(4) не учитывается в расчетах
Конечная продукция в межотраслевом балансе -
(1) продукция, не требующая дальнейшей переработки,
(2) валовая продукция за вычетом экспорта
(3) продукция, направляемая вне сферы производственного потребления
(4) сумма валовой и промежуточной продукции каждой отрасли экономической системы
В качестве управляемых переменных в оптимизационных моделях в экономике используются:
(1) планируемые объёмы выпуска продукции,
(2) показатели затрат на производство,
(3) показатели, которые надо найти при решении задачи,
(4) прибыль от реализации различных видов продукции
Что такое стохастические переменные?
(1) зависят от времени,
(2) не могут быть точно установлены,
(3) применяются для построения регрессии,
(4) заранее известны
Функция принадлежности нечеткого множества ![math]() , определенного на множестве
, определенного на множестве ![math]() , это:
, это:
 , определенного на множестве
, определенного на множестве  , это:
, это:
(1) функция, которая устанавливает значения степени принадлежности нечеткому множеству ![math]() каждого из элементов универсального множества
каждого из элементов универсального множества ![math]() и принимает лишь два значения: 0 или 1
и принимает лишь два значения: 0 или 1
 каждого из элементов универсального множества
каждого из элементов универсального множества  и принимает лишь два значения: 0 или 1
и принимает лишь два значения: 0 или 1
(2) функция, которая устанавливает значения степени принадлежности нечеткому множеству ![math]() каждого из элементов универсального множества
каждого из элементов универсального множества ![math]() и принимает значения > 0
и принимает значения > 0
 каждого из элементов универсального множества
каждого из элементов универсального множества  и принимает значения > 0
и принимает значения > 0
(3) функция, которая устанавливает значения степени принадлежности нечеткому множеству ![math]() каждого из элементов универсального множества
каждого из элементов универсального множества ![math]() и принимает значения на отрезке
и принимает значения на отрезке ![math]()
 каждого из элементов универсального множества
каждого из элементов универсального множества  и принимает значения на отрезке
и принимает значения на отрезке 
(4) функция, которая устанавливает значения степени принадлежности нечеткому множеству ![math]() каждого из элементов универсального множества
каждого из элементов универсального множества ![math]() и принимает значение, равное 1
и принимает значение, равное 1
 каждого из элементов универсального множества
каждого из элементов универсального множества  и принимает значение, равное 1
и принимает значение, равное 1 Экстремальное значение функции ![math]() равно:
равно:
 равно:
равно:
(1) 2.816
(2) 1.816
(3) 0.816
(4) не существует
Выражение ![math]() лежит в основе расчета:
лежит в основе расчета:
 лежит в основе расчета:
лежит в основе расчета:
(1) современной стоимости элементарного денежного потока
(2) будущей стоимости элементарного денежного потока
(3) срока финансовой операции
(4) будущей стоимости финансовой ренты
Структура конечного продукта МОБ состоит из компонентов :
(1) конечное потребление + инвестиции +чистый экспорт
(2) конечное потребление + инвестиции + прибыль
(3) конечное потребление +оплата труда + налоги
(4) инвестиции +оплата труда +чистый экспорт
В задаче оптимальной производственной программы структура выпуска – это:
(1) пропорции затрат ресурсов
(2) объемы изделий, вошедших в выпуск
(3) перечень изделий, вошедших в выпуск
(4) перечень изделий, не вошедших в выпуск
Моделирование последовательностей случайных величин использует
(1) статистические функции,
(2) генератор случайных величин
(3) плотность вероятности случайных величин,
(4) корреляцию случайных величин
Нечеткое множество ![math]() называют нормальным,
называют нормальным,
 называют нормальным,
называют нормальным,
(1) если минимальное значение функции принадлежности ![math]() равно 0
равно 0
 равно 0
равно 0
(2) если максимальное значение функции принадлежности ![math]() равно 1
равно 1
 равно 1
равно 1
(3) если максимальное значение функции принадлежности ![math]() больше 1
больше 1
 больше 1
больше 1
(4) если максимальное значение функции принадлежности ![math]() меньше 1
меньше 1
 меньше 1
меньше 1 Функция ![math]() имеет перегиб при значении
имеет перегиб при значении
 имеет перегиб при значении
имеет перегиб при значении x, равном:
(1) 0,223
(2) 1,223
(3) 2,223
(4) 3,223
Выражение для современной стоимости постоянной финансовой ренты имеет вид:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой смысл имеют элементы матрицы полных затрат
bij:
(1) объем продукции i-й отрасли, расходуемый на производство единицы продукции конечной продукции j-й отрасли
(2) часть общего валового продукта , израсходованная на производственные нужды в процессе производства
(3) объем валового продукта i-й отрасли на производство единицы конечного продукта j-й отрасли
(4) объем продукции i-й отрасли, расходуемый на производство единицы валовой продукции продукции j-й отрасли
Если в оптимизационной задаче поиска максимума целевой функции все условия ограничивают переменные снизу, то результат будет:
(1) значения целевой ячейки не сходятся
(2) множество решений
(3) решение найдено
(4) система не может найти решение
Результаты имитационного эксперимента могут быть использованы
(1) для построения прогнозных сценариев,
(2) для определения постоянных показателей,
(3) для определения оптимальных показателей,
(4) для оценки рисков.
Выберите носитель для нечеткого множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Действие функции
stack (M1,M2) над матрицами M1 и M2 :
(1) объединяет в одну
М1 и М2, имеющие одинаковое число столбцов
(2) объединяет в одну
М1 и М2, имеющие одинаковое число строк
(3) вычисляет вектор обобщенных собственных чисел
М1 и М2
(4) сортирует матрицы
М1 и М2 Финансовая рента пренумерандо - рента, для которой:
(1) только первый платеж осуществляется в начале первого периода,
(2) каждый платеж осуществляется в начале каждого периода
(3) каждый платеж осуществляется в конце каждого периода
(4) первый платеж осуществляется в конце первого периода
Коэффициент полных затрат труда это:
(1) разность затрат живого и овеществленного труда на производство конечной продукции
(2) затраты живого и овеществленного труда на производство единицы общего объема произведенной продукции
(3) затраты живого и овеществленного труда на производство единицы конечной продукции
(4) отношение общего объема произведенной продукции к затратам живого и овеществленного труда на его производство
Пусть на трех складах хранится однотипная продукция ![math]() , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве ![math]() , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей ![math]() . Оптимальные минимальные затраты транспортировки составляют:
. Оптимальные минимальные затраты транспортировки составляют:
 , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей  . Оптимальные минимальные затраты транспортировки составляют:
. Оптимальные минимальные затраты транспортировки составляют:
(1) 4120 ед.,
(2) 4130 ед.,
(3) 4140 ед.,
(4) 4150 ед.
При использовании Монте-Карло неопределенные данные задаются как:
(1) оценочные с учетом условий,
(2) средние с доверительным интервалом,
(3) случайные величины,
(4) случайные величины с определенным законом распределения.
Выберите точку перехода для нечеткого множества ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для системы уравнений ![math]() корень решения
корень решения
 корень решения
корень решения x равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Ссуда в 4000 ед. получена под ставку 10% в год. Через два года возвращаемая сумма составит:
(1) 4687 ед.
(2) 4587 ед.
(3) 4487 ед.
(4) 4387 ед.
Коэффициент полных затрат продукции – это:
(1) объем продукции i-й отрасли, расходуемый на производство единицы валовой продукции j-й отрасли
(2) часть общего валового продукта , израсходованная на производственные нужды в процессе производства
(3) объем продукции i-й отрасли, расходуемый на производство единицы продукции конечной продукции j-й отрасли
(4) объем валового продукта i-й отрасли на производство единицы конечного продукта j-й отрасли
В транспортной задаче с промежуточными пунктами тариф транспортировки от первичного поставщика к конечному потребителю принимается равным:
(1) нулю
(2) единице
(3) большому нереальному тарифу
(4) сумме тарифов от первого поставщика до промежуточного и от промежуточного до конечного потребителя
Для компьютерной имитации параметра имитационной модели в Mathcad используется функция:
(1)
rnorm( ),
(2)
runif( ),
(3)
rnd( ).
(4) выбранного закона распределения.
Множество ![math]() –уровня для нечеткого множества
–уровня для нечеткого множества ![math]() составляется для:
составляется для:
 –уровня для нечеткого множества
–уровня для нечеткого множества  составляется для:
составляется для:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная ![math]() для функций, заданных параметрически:
для функций, заданных параметрически: ![math]() равна:
равна:
 для функций, заданных параметрически:
для функций, заданных параметрически:  равна:
равна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чистая современная (приведенная) стоимость определяется как :
(1) разность между приведенным на момент инвестирования потоком платежей и инвестициями,
(2) разность между суммой всех платежей и инвестициями,
(3) приведенный на момент инвестирования поток платежей,
(4) разность между суммой всех платежей и приведенным потоком платежей.
Валовый продукт ![math]() , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции ![math]() . Общие затраты труда составят:
. Общие затраты труда составят:
 , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции  . Общие затраты труда составят:
. Общие затраты труда составят:
(1) 1200
(2) 1140
(3) 1160
(4) 1180
Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны ![math]() . Нормы прибыли (в усл.ед) от реализации каждого вида равны
. Нормы прибыли (в усл.ед) от реализации каждого вида равны ![math]() . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей ![math]() , для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
, для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
 . Нормы прибыли (в усл.ед) от реализации каждого вида равны
. Нормы прибыли (в усл.ед) от реализации каждого вида равны  . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  , для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
, для получения оптимальной максимальной прибыли надо отказаться от выпуска продукции:
(1) 1 вида
(2) 2 вида
(3) 3 вида
(4) 1 и 2 вида
При анализе результатов имитационного эксперимента мерой рисковых значений для выходного показателя является:
(1) вероятностное распределение всех возможных его значений,
(2) дисперсия,
(3) коэффициент вариации ,
(4) среднеквадратичное отклонение.
Как называется функция принадлежности, описываемая законом
(1) треугольная
(2) трапециевидная
(3) гауссова
(4) Z-образная
Для функции, заданной в виде ![math]() , значение
, значение ![math]() равно:
равно:
 , значение
, значение  равно:
равно:
(1) 0,686
(2) 0,586
(3) 0,486
(4) 0,386
Сумма 1000 ед. вырастет до 5000 ед. при вложении в банк под ставку 8% годовых с ежемесячным начислением процентов за срок:
(1) 10 лет
(2) 15 лет
(3) 20 лет
(4) 25 лет
Коэффициенты прямых затрат должны удовлетворять следующим условиям:
(1) все коэффициенты прямых затрат неотрицательны ![math]()

(2) все коэффициенты прямых затрат ![math]()

(3) все коэффициенты прямых затрат ![math]()

(4) сумма элементов матрицы A по любому столбцу меньше единицы
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый, и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. При оптимизации полного фонда оплаты (минимальный) минимальный фонд (оплата всех сотрудников) составит:
(1) 220 ед.
(2) 230 ед.
(3) 240 ед.
(4) 250 ед.
Для оценки риска выходному показателю принять значение больше (меньше) заданного используется функция:
(1)
rnorm( )
(2)
runif( )
(3)
rnd( )
(4) полученного закона распределения
Для какого нечеткого множества приведенное множество ![math]() является ближайшим к нечеткому.
является ближайшим к нечеткому.
 является ближайшим к нечеткому.
является ближайшим к нечеткому.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть производительность труда от времени ![math]() , объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
t характеризуется функцией  , объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за второй час рабочего дня составит:
(1) 1,6
(2) 2,6
(3) 3,6
(4) 4,6
Выражение ![math]() лежит в основе расчета
лежит в основе расчета
 лежит в основе расчета
лежит в основе расчета
(1) периодического платежа финансовой ренты пренумерандо
(2) периодического платежа финансовой ренты постнумерандо
(3) срока накопления финансовой ренты пренумерандо
(4) срока накопления финансовой ренты постнумерандо.
Конечный продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи в "комплектной постановке" (использование только имеющихся ресурсов) в качестве управляемых переменных выбираются:
(1) количества выпускаемой продукции
(2) количества выпускаемой продукции и доля выполнения плана
(3) суммарное количество используемых ресурсов
(4) доля выполнения плана
Для анализа результатов имитационного эксперимента необходимо:
(1) +рассчитать статистические характеристики выходного показателя,
(2) рассчитать статистические характеристики входных показателей,
(3) +построить распределение выходного показателя.
(4) построить распределение входных показателей
Выбрать нечеткое множество, для которого супремум=0,8
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция спроса имеет вид ![math]() , функция предложения
, функция предложения ![math]() , где
, где ![math]() и
и ![math]() – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, ![math]() - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
 , функция предложения
, функция предложения  , где
, где 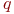 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
(1) 1,5
(2) 2,5
(3) 3,5
(4) 4,5
Сумма 5000 руб., за 2,5 года выросла до 7000 руб. при начислении сложных процентов, доходность операции составила:
(1) 6305 ед.
(2) 6205 ед.
(3) 6105 ед.
(4) 6005 ед.
Валовый продукт ![math]() , матрица межотраслевых поставок
, матрица межотраслевых поставок ![math]() . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
 , матрица межотраслевых поставок
, матрица межотраслевых поставок  . Вектор добавленной стоимости равен:
. Вектор добавленной стоимости равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При решении задачи с добавлением ресурсов - в качестве управляемых переменных выбираются:
(1) значения количеств выпускаемой продукции
(2) значения количеств выпускаемой продукции и значения дополнительных ресурсов каждого вида
(3) суммарное количество используемых ресурсов
(4) значения дополнительных ресурсов каждого вида
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов:
1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Детерминированные переменные задачи:
(1) доходы по годам
(2) сумма кредита
(3) процентная ставка дисконтирования
(4) расходы
Какие инструменты MathCad можно использовать для построения множества a–уровня для нечеткого множества А (U,mA)
(1) встроенные функции категории Statistics (Статистика)
(2) операции с матрицами
(3) функция
if ()
(4) символьное решение уравнений
Спрос на товары второй необходимости выражается функцией Торнквиста ![math]() , где
, где ![math]() - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
 , где
, где  - доход, предельный спрос при увеличении дохода составит:
- доход, предельный спрос при увеличении дохода составит:
(1) 10
(2) 20
(3) 30
(4) 40
На депозит отчисляются суммы в размере 3000 каждый квартал под ставку 10% годовых. Проценты начисляются ежеквартально с капитализацией. Сумма к концу 2 года составит:
(1) 26108 ед.
(2) 26208 ед.
(3) 26308 ед.
(4) 26408 ед.
Валовый продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() , затраты живого труда
, затраты живого труда ![math]() , вектор полной трудоемкости
, вектор полной трудоемкости
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  , затраты живого труда
, затраты живого труда  , вектор полной трудоемкости
, вектор полной трудоемкости T равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны ![math]() . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны ![math]() . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей ![math]() . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
 . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны  . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 1 вида составит:
(1) 110
(2) 120
(3) 130
(4) 140
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, в результате исследования за ожидаемое значение чистой приведенной стоимости прибыли следует принять:
(1) среднее +/- среднеквадратичное значение ,
(2) максимальное значение,
(3) минимальное значение,
(4) среднеквадратичное значение
Дано нечеткое множество ![math]() . Индекс нечеткости
. Индекс нечеткости ![math]() по линейной метрике равен:
по линейной метрике равен:
 . Индекс нечеткости
. Индекс нечеткости  по линейной метрике равен:
по линейной метрике равен:
(1) 0,34
(2) 0,68
(3) 0,92
(4) 1,7
Функция ![math]() при x>0 имеет экстремум при значении
при x>0 имеет экстремум при значении
 при x>0 имеет экстремум при значении
при x>0 имеет экстремум при значении x, равном:
(1) 0
(2) 1
(3) 2
(4) не существует
Будущая стоимость платежа при увеличении количества начислений сложных процентов в течение года:
(1) увеличивается
(2) уменьшается
(3) остается постоянной
(4) зависит от ….
Валовая продукция в межотраслевом балансе:
(1) суммарная продукция каждой отрасли, произведённая в рамках экономической системы
(2) разность конечной и промежуточной продукции
(3) конечная продукция каждой отрасли, умноженная на коэффициент прямых затрат этой отрасли
(4) конечная продукция каждой отрасли, умноженная на коэффициент полных затрат этой отрасли
Количество аргументов целевой функции в оптимизационной задаче равно:
(1) количеству ресурсов
(2) количеству управляемых переменных
(3) количеству плановых ограничений
(4) целевым коэффициентам
Функции стохастических аргументов являются
(1) детерминированными,
(2) стохастическими,
(3) оптимизационными,
(4) статистическими.
Имеется нечеткое множество ![math]() . Выбрать множество значений функции принадлежности
. Выбрать множество значений функции принадлежности ![math]() для него:
для него:
 . Выбрать множество значений функции принадлежности
. Выбрать множество значений функции принадлежности  для него:
для него:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Экстремальное значение функции ![math]() для
для
 для
для x>0 равно:
(1) 0,25
(2) 1,25
(3) 2,5
(4) не существует
Выражение ![math]() лежит в основе расчета:
лежит в основе расчета:
 лежит в основе расчета:
лежит в основе расчета:
(1) современной стоимости элементарного денежного потока,
(2) процентной ставки элементарного денежного потока,
(3) срока финансовой операции,
(4) периодического платежа финансовой ренты.
Структура добавленной стоимости МОБ состоит из компонентов:
(1) оплата труда + чистая прибыль + чистый экспорт
(2) конечное потребление + чистая прибыль + налоги
(3) чистая прибыль +оплата труда + инвестиции
(4) оплата труда + чистая прибыль + налоги
Оптимизационная задача в Mathcad может быть решена с помощью:
(1) функции
lsolve()
(2) блока
Given Find()
(3) блока
Given Maximize ()
(4) блока
Given Minimaze() При имитационном моделировании необходимо задать:
(1) среднее значение ключевых переменных,
(2) дисперсию ключевых переменных,
(3) закон распределения ключевых переменных,
(4) коэффициент корреляции ключевых переменных
Нечеткое множество ![math]() называют субнормальным, -
называют субнормальным, -
 называют субнормальным, -
называют субнормальным, -
(1) если минимальное значение функции принадлежности ![math]() равно 0
равно 0
 равно 0
равно 0
(2) если максимальное значение функции принадлежности ![math]() равно 1
равно 1
 равно 1
равно 1
(3) если максимальное значение функции принадлежности ![math]() больше 1
больше 1
 больше 1
больше 1
(4) если максимальное значение функции принадлежности ![math]() меньше 1
меньше 1
 меньше 1
меньше 1 Функция ![math]() имеет перегиб (для
имеет перегиб (для
 имеет перегиб (для
имеет перегиб (для x>0 ) при значении x, равном:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выражение для наращенной стоимости элементарного потока имеет вид:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Коэффициент прямых затрат производства продукции это:
(1) отношение количества продукции i-й отрасли для производства j-й отрасли к конечному продукту j-й отрасли
(2) отношение количества продукции i-й отрасли для производства j-й отрасли к валовому продукту j-й отрасли
(3) отношение валового продукта i-й к отрасли к количеству продукции i-й отрасли для производства j-й отрасли
(4) отношение конечной продукции i-й отрасли к валовому продукту j-й отрасли
Если в оптимизационной задаче поиска минимума целевой функции все условия ограничивают переменные сверху, то результат будет:
(1) значения целевой ячейки не сходятся
(2) множество решений
(3) решение найдено
(4) система не может найти решение
В методе Монте-Карло учитывается влияние на исследуемую систему:
(1) постоянного возмущения,
(2) взаимодействия внутри системы,
(3) недостатка параметров,
(4) случайных факторов
Множество имеет вид ![math]() . Для какого нечеткого множества оно является несущим :
. Для какого нечеткого множества оно является несущим :
 . Для какого нечеткого множества оно является несущим :
. Для какого нечеткого множества оно является несущим :
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() определяет:
определяет:
 определяет:
определяет:
(1) число элементов вектора ![math]()

(2) перестановку элементов вектора ![math]() в обратном порядке
в обратном порядке
 в обратном порядке
в обратном порядке
(3) индекс последнего элемента вектора ![math]()

(4) сортировку элементов вектора ![math]()

Финансовая рента постнумерандо - рента, для которой:
(1) только первый платеж осуществляется в начале первого периода,
(2) каждый платеж осуществляется в начале каждого периода
(3) каждый платеж осуществляется в конце каждого периода
(4) только первый платеж осуществляется в конце первого периода
Если
t и T – векторы прямой и полной трудоемкости, X и Y – векторы - валовой и конечной продукции, то уравнение межотраслевого баланса труда имеет вид.
(1)
T=tX+TY
(2)
T=tX+Y
(3)
tY =TX
(4)
tX=TY Пусть на трех складах хранится однотипная продукция ![math]() , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве ![math]() , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей ![math]() . Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
. Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
 , три потребителя сделали заказ на продукцию в количестве
, три потребителя сделали заказ на продукцию в количестве  , тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей
, тарифы перевозки единицы груза из пункта отправления в пункт назначения задаются матрицей  . Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
. Для обеспечения минимальных затрат 1 потребителю необходимо получить груз:
(1) только с 1 склада,
(2) только с 2 склада,
(3) только с 3 склада,
(4) со всех трех складов.
Результаты имитационного моделирования могут быть использованы для:
(1) оценки рисков,
(2) рейтингового анализа,
(3) определения оптимального детерминированного значения показателя,
(4) принятия управленческого решения.
Выберите нечеткое множество, для которого точка перехода это элемент {1}
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для системы уравнений ![math]() корень решения
корень решения
 корень решения
корень решения y равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какой показатель является устойчивым в плановом периоде относительно отчётного периода:
(1) количество промежуточной продукции каждой из отраслей
(2) количество конечной продукции каждой из отраслей
(3) коэффициенты прямых затрат продукции каждой из отраслей
(4) количество валовой продукции каждой из отраслей
В транспортной задаче, когда общее количество груза больше, чем требуется потребителям, вводится
(1) дополнительный потребитель
(2) дополнительный поставщик
(3) добавляется стоимость транспортировки
(4) уменьшается стоимость транспортировки
Для компьютерной имитации параметров имитационной модели в Mathcad используются функции из категории:
(1) probaility distribution;
(2) random numbers;
(3) hrobability density
(4) statistics.
Дано нечеткое множество
![math]() Множеством
Множеством ![math]() уровня является множество:
уровня является множество:
 Множеством
Множеством  уровня является множество:
уровня является множество:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная ![math]() для функций, заданных параметрически:
для функций, заданных параметрически: ![math]() равна:
равна:
 для функций, заданных параметрически:
для функций, заданных параметрически:  равна:
равна:
(1) 3
(2) ![math]()

(3) ![math]()

(4) ![math]()

При расчете наращенной суммы за n периодов по схеме сложных процентов
(1) проценты начисляются
n раз на начальную денежную сумму и накопленные проценты
(2) проценты начисляются
n раз на начальную денежную сумму
(3) проценты начисляются 1 раз на начальную денежную сумму и накопленные проценты
(4) проценты начисляются
(n +1) раз на первоначальную денежную сумму и накопленные проценты Конечный продукт ![math]() , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ ![math]() , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции ![math]() . Общие затраты труда составят:
. Общие затраты труда составят:
 , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ  , коэффициенты прямых затрат труда на единицу продукции
, коэффициенты прямых затрат труда на единицу продукции  . Общие затраты труда составят:
. Общие затраты труда составят:
(1) 1300
(2) 1310
(3) 1320
(4) 1330
Результат имитационного эксперимента зависит:
(1) от заданных распределений стохастических переменных,
(2) от размера выборки,
(3) от метода генерации,
(4) от параметров заданных распределений стохастических переменных
Определите основные типы функций принадлежности:
(1) треугольные
(2) трапециевидные
(3) гауссовы
(4) ромбовые
Для функции, заданной в виде ![math]() , значение
, значение ![math]() равно:
равно:
 , значение
, значение  равно:
равно:
(1) 0,52
(2) 1,52
(3) 2,52
(4) 3,52
Сумма 5000 ед. вырастет до 10000 ед. при вложении в банк под ставку 10% годовых с ежеквартальным начислением процентов за срок:
(1) 5 лет
(2) 8 лет
(3) 6 лет
(4) 7лет
Какой смысл имеют элементы матрицы ![math]() .
.
 .
.
(1) объем продукции i-й отрасли , расходуемый на производство конечной продукции j-й отрасли
(2) часть общего валового продукта , израсходованная на производственные нужды в процессе производства
(3) затраты валового продукта i-й отрасли на производство единицы конечного продукта j-й отрасли
(4) объем продукции i-й отрасли, расходуемый j-й отраслью в процессе производствa
Для выполнения проекта фирме требуется провести 3 этапа работ. На 1 этапе требуются инженеры с оплатой 30 ед. каждый и программисты с оплатой 40 ед. На 2 этапе требуются инженеры, программисты и менеджеры с оплатой 20 ед, на 3 этапе требуются программисты и менеджеры. Всего требуется на 1 этапе 6 сотрудников, на 2 этапе 8 сотрудников на 3 этапе 3 сотрудника. При оптимизации полного фонда оплаты (минимальный) оплата инженеров составит:
(1) 90 ед.
(2) 60 ед.
(3) 120ед.
(4) 150 ед.
Процентный разброс исследуемого показателя около среднего значения определяет:
(1) дисперсия
(2) коэффициент вариации
(3) среднеквадратичное отклонение
(4) (максимальное значение – минимальное значение)
Обычным множеством, ближайшим к нечеткому множеству ![math]() , называется:
подмножество
, называется:
подмножество ![math]() множества U, характеристическая функция которого имеет вид:
множества U, характеристическая функция которого имеет вид:
 , называется:
подмножество
, называется:
подмножество  множества U, характеристическая функция которого имеет вид:
множества U, характеристическая функция которого имеет вид:
(1)
(2)
(3)
(4)
Пусть производительность труда от времени ![math]() , объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
t характеризуется функцией  , объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
, объем произведенной работы (в усл. ед.) за третий час рабочего дня составит:
(1) 1,6
(2) 2,6
(3) 3,6
(4) 4,6
Выражение ![math]() лежит в основе расчета
лежит в основе расчета
 лежит в основе расчета
лежит в основе расчета
(1) периодического платежа финансовой ренты пренумерандо
(2) периодического платежа финансовой ренты постнумерандо
(3) срока накопления финансовой ренты пренумерандо
(4) срока накопления финансовой ренты постнумерандо
Конечный продукт ![math]() , матрица прямых затрат МОБ
, матрица прямых затрат МОБ ![math]() . Матрица межотраслевых поставок имеет вид:
. Матрица межотраслевых поставок имеет вид:
 , матрица прямых затрат МОБ
, матрица прямых затрат МОБ  . Матрица межотраслевых поставок имеет вид:
. Матрица межотраслевых поставок имеет вид:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается задача оптимальной производственной программы с заданным планом при нехватке имеющихся ресурсов. При построении оптимизационной модели в "комплектной постановке" задача имеет решение:
(1) в зависимости от целевой функции
(2) в зависимости от ресурсов
(3) в зависимости от плана
(4) всегда
При анализе результатов имитационного эксперимента за ожидаемое значение выходного показателя следует принять:
(1) среднее +/- среднеквадратичное значение ,
(2) максимальное значение,
(3) минимальное значение,
(4) среднеквадратичное значение.
Выбрать супремум для нечеткого множества: ![math]()

(1) 0
(2) 1
(3) 0,9
(4) 10
Функция спроса имеет вид ![math]() , функция предложения
, функция предложения ![math]() , где
, где ![math]() и
и ![math]() – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени, ![math]() - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
 , функция предложения
, функция предложения  , где
, где 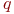 и
и  – количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,
– количество товара, соответственно покупаемого и предлагаемого на продажу в единицу времени,  - цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
- цена товара. Равновесная цена, при которой спрос и предложение уравновешиваются равна:
(1) 1
(2) 2
(3) 3
(4) 4
Банк принимает вклады под 8% годовых, проценты начисляются ежемесячно с учетом капитализации, эффективная годовая процентная ставка составит:
(1) 8,1%.
(2) 8,2%.
(3) 8,3%.
(4) 8,4%.
Валовый продукт ![math]() , матрица межотраслевых поставок
, матрица межотраслевых поставок ![math]() . матрица прямых затрат равна:
. матрица прямых затрат равна:
 , матрица межотраслевых поставок
, матрица межотраслевых поставок  . матрица прямых затрат равна:
. матрица прямых затрат равна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассматривается оптимизационная задача выполнения производственной программы с заданным планом при нехватке имеющихся ресурсов. При построении оптимизационной модели с добавлением ресурсов задача имеет решение:
(1) в зависимости от целевой функции
(2) в зависимости от ресурсов
(3) в зависимости от плана
(4) всегда
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов:
1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель. Выходной исследуемый показатель:
(1) прибыль с учетом затрат по годам
(2) чистая приведенная стоимость прибыли
(3) процентная ставка дисконтирования
(4) затраты
Какие инструменты MathCad можно использовать для представления нечеткого множества:
(1) операции с матрицами
(2) функция
if ()
(3) блок программирования
(4) символьное решение уравнений
Спрос на товары второй необходимости, который выражается функцией Торнквиста ![math]() , где
, где ![math]() - доход, появляется, если доход достигнет величины :
- доход, появляется, если доход достигнет величины :
 , где
, где  - доход, появляется, если доход достигнет величины :
- доход, появляется, если доход достигнет величины :
(1) 10
(2) 20
(3) 30
(4) 40
В банк отчисляются суммы в размере 2000 в начале каждого месяца под ставку 8% годовых. Проценты начисляются ежемесячно с капитализацией. Сумма к концу года составит:
(1) 25140 ед.
(2) 25240 ед.
(3) 25340 ед.
(4) 25440 ед.
Валовый продукт ![math]() , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ ![math]() , затраты живого труда
, затраты живого труда ![math]() , вектор полной трудоемкости
, вектор полной трудоемкости
 , матрица межотраслевых поставок МОБ
, матрица межотраслевых поставок МОБ  , затраты живого труда
, затраты живого труда  , вектор полной трудоемкости
, вектор полной трудоемкости Т равен:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Предприятие выпускает три вида продукции, используя два типа ресурсов, запасы которых равны ![math]() . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны ![math]() . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей ![math]() . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
 . Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны
. Нормы прибыли (в усл.ед) от реализации каждого вида продукции равны  . Расход ресурсов при производстве задается матрицей
. Расход ресурсов при производстве задается матрицей  . Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
. Поступил новый заказ на продукцию 2 вида – 70 (ед), продукцию 3 вида – 80 (ед). Чтобы выполнить полный заказ, добавляются ресурсы, оптимальное минимальное количество добавочных ресурсов 2 вида составит :
(1) 360
(2) 370
(3) 380
(4) 390
Предприятие планирует взять кредит в размере 4 млн. руб. по ставке 15% годовых и инвестировать в модернизацию в производстве. По оценкам это приведет в течение трех лет к поступлению следующих доходов: 1 год – от 1500 – до 2000 (тыс. руб.), 2 год – 2000 - 4000 (тыс. руб.) 3 год – 5500 – 7000 тыс. руб. Общепроизводственные расходы составляют от 20% до 25% от поступлений в год. Для оценки проекта строится имитационная модель, для измерения риска проекта следует определить:
(1) дисперсию прибыли,
(2) максимальное значение прибыли,
(3) минимальное значение прибыли,
(4) вероятность чистой приведенной стоимости прибыли быть <0
Даны два нечетких множества ![math]() и
и ![math]() Сравнить индексы нечеткости по линейной метрике:
Сравнить индексы нечеткости по линейной метрике:
 и
и  Сравнить индексы нечеткости по линейной метрике:
Сравнить индексы нечеткости по линейной метрике:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нельзя сравнивать
Выберите нечеткое множеств, которое является нормальным:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()
