Главная / Математика / Линейные дифференциальные уравнения и системы

Линейные дифференциальные уравнения и системы - ответы на тесты Интуит

Правильные ответы выделены зелёным цветом.
Все ответы: Курс лекций посвящен изложению методов и теории дифференциальных уравнений.
Смотрите также:
Физика
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a1
d2
k?
b-23
x5
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
10
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b1
C?
X04
Y04,5
В ответе укажите недостающий параметр.
4
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
7
Найти корни характеристического уравнения: math. В ответе указать наименьший из корней.
a-2
b2
c4
-1
Дано уравнение math.
a2
b-8
c-1
f6
g45
Найти значение его кратного корня.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-2
b2
c4
A10
B8
Убедитесь, что общее решение однородного уравнения имеет вид: math. Решить задачу Коши. В ответе привести значение math.
4
Задано неоднородное линейное дифференциальное уравнение: math
a-2
b2
c12
D24
F-112
K12
K25
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение A.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y'''+4x^2y''+49xy'-60y=-420-55x\\ y(0)=6;\\ y’(0)=26;\\ y’’(0)=90. Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
3
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: mathНайти замену переменных math math где math и math постоянные величины.
A11
b13
c11
a10
b4
c5
В ответе указать значение math.
1
Задано уравнение: math
k2
b3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,6
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
-4
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a1
d2
k?
b-23
x5
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
27
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a6
b2
C?
X03
Y06
В ответе укажите недостающий параметр.
5
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
5
Найти корни характеристического уравнения: math. В ответе указать наименьший из корней.
a-2
b2
c4
2
Дано уравнение math.
a2
b-8
c-1
f6
g45
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-2
b2
c4
A10
B8
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
6
Задано неоднородное линейное дифференциальное уравнение: math
a-2
b2
c12
D24
F-112
K12
K25
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение B.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
4
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
math Найти замену переменных math math где math и math постоянные величины.
A11
b13
c11
a10
b4
c5
В ответе указать значение math.
7
Задано уравнение: math
k-3
b3
c2
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-2,5
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
8
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a1
d2
k?
b-23
x5
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
10
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b4
C?
X05
Y07,5
В ответе укажите недостающий параметр.
5
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
7
Задано характеристическое уравнение: math.
a1
b-1
c-10
d-8
Найти его корни. В ответе указать наименьший из них.
-2
Дано уравнение math.
a2
b-8
c-36
f216
g-270
Найти значение его кратного корня.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math math – нумеруются в порядке возрастания. В ответе указать значение math.
-2
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
5
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A16
b18
c158
a2
b6
c36
В ответе указать значение math.
3
Задано уравнение: math
k-2
b-3
c-5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,6
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
4
Найти производную функции math
(1) math>
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k32
b-98
x7
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
4
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a2
b7
C4
X01
Y0?
В ответе укажите недостающий параметр.
7,5
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
-8
Задано характеристическое уравнение: math.
a1
b-1
c-10
d-8
Найти его корни. В ответе указать средний по величине из них.
-1
Дано уравнение math.
a2
b-8
c-36
f216
g-270
Найдите кратный корень. В ответе укажите его кратность.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y'''+4x^2y''+49xy’-60cy=-420+-55x\\ y(0)=6;\\ y'(0)=26;\\ y''(0)=90. Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
1
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A16
b18
c158
a2
b6
c36
В ответе указать значение math.
5
Задано уравнение: math
k-2
b-3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,4
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
2,5
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k32
b-98
x7
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
126
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a10
b4
C8
X05
Y0?
В ответе укажите недостающий параметр.
10
Вычислить значение определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
7
Задано характеристическое уравнение: math.
a1
b-1
c-10
d-8
Найти его корни. В ответе указать наибольший из них.
4
Дано уравнение math.
a125
b-980
c1844
f288
g64
Найти значение его кратного корня.
4
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
2
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A12
b17
c114
a12
b3
c6
В ответе указать значение math.
0
Задано уравнение: math
k3
b2
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,25
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
2
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k32
b-98
x7
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
32
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a12
b5
C4
X0?
Y05,25
В ответе укажите недостающий параметр.
3
Вычислить значение производной определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a113
b114
c115
a126
b127
c126
a215
b214
c213
a224
b226
c225
5
Найти уравнение вида: math , которому удовлетворят следующие три корня:
3
5
7
В ответе указать значениеmath.
15
Дано уравнение math.
a125
b-980
c1844
f288
g64
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
6
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
3
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A12
b17
c114
a12
b3
c6
В ответе указать значение math.
2
Задано уравнение: math
k6
b7
c-4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-2,5
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
3
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a1
d2
k?
b-23
x5
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
3
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a4
b1
C2
X0?
Y02,75
В ответе укажите недостающий параметр.
3
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a113
b115
a124
b121
a136
b137
a212
b216
a228
b222
a234
b238
a312
b314
a326
b323
a335
b336
16
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
3
5
7
В ответе указать значение math.
71
Дано уравнение math.
a125
b-980
c1844
f288
g64
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение r.
-0,08
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение А.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
5
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A12,5
b14,3
c165,5
a2,8
b3,1
c21,1
В ответе указать значение math.
2
Задано уравнение: math
k4
b6
c8
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,5
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
4
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a1
d2
k?
b-23
x5
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
42
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=ae^p\\ y=be^p+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b2
C3
X0?
Y04,5
В ответе укажите недостающий параметр.
6
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a113
b115
a124
b121
a136
b137
a212
b216
a228
b222
a234
b238
a312
b314
a326
b323
a335
b336
40
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
3
5
7
В ответе указать значение math.
-105
Дано уравнение math.
a125
b-980
c1844
f288
g64
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение math.
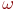0,16
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-6
b11
c-6
A6
B11
C25
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-2
b2
c12
d28
f68
k2
G10
H10
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение В.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b49
c-60
A-420
B-55
F6
G26
H90
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
7
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A12,5
b14,3
c165,5
a2,8
b3,1
c21,1
В ответе указать значение math.
5
Задано уравнение: math
k5
b-3
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
0,25
Задано уравнение вида: math
k2,5
n2
m4
l6
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию math.
-8
Найти производную функции math
(1) math
(2) math
(3) math
(4) math
(5) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
d?
k24
b-47
x4
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
1
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b1
C4
X0?
Y04,5
В ответе укажите недостающий параметр.
4
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-20
Найти корни характеристического уравнения: math. . В ответе указать наименьший из корней.
a-1
b3
c4
-1
Дано уравнение math.
a4
b-15
c15
f-8
g12
Найти значение его кратного корня.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-1
b3
c4
A5
B5
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задано неоднородное линейное дифференциальное уравнение: math
a-1
b6
c-8
D3
F-12
K13
K21
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение A.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
3
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: mathНайти замену переменных math math где math и math постоянные величины.
A12
b13
c118
a1
b3
c15
В ответе указать значение math.
3
Задано уравнение: math
k2
b3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,4
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
8
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
d?
k24
b-47
x4
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
49
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a6
b2
C5
X0?
Y06
a6
b2
C5
X0?
Y06
В ответе укажите недостающий параметр.
3
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-71
Найти корни характеристического уравнения: math. В ответе указать наименьший из корней.
a-1
b3
c4
4
Дано уравнение math.
a4
b-15
c15
f-8
g12
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-1
b3
c4
A5
B5
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задано неоднородное линейное дифференциальное уравнение: math
a-1
b6
c-8
D3
F-12
K13
K21
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение B.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
6
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где (x+) и (y+) постоянные величины.
A12
b13
c118
a1
b3
c15
В ответе указать значение math.
4
Задано уравнение: math
k-3
b3
c2
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
0,5
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
2
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
d?
k24
b-47
x4
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
24
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b4
C5
X0?
Y07,5
В ответе укажите недостающий параметр.
5
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-20
Задано характеристическое уравнение: math.
a2
b-20
c62
d-60
Найти его корни. В ответе указать наименьший из них.
2
Дано уравнение math.
a4
b-15
c-6
f76
g-72
Найти значение его кратного корня.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
7
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A11
b10
c14
a4
b7
c65
В ответе указать значение math.
4
Задано уравнение: math
k-2
b-3
c-5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,4
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
0,8
Найти производную функции math
(1) math>
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
c2
k?
b-48
x4
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
26
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a2
b7
C4
X0?
Y07,5
В ответе укажите недостающий параметр.
1
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-87
Задано характеристическое уравнение: math.
a2
b-20
c62
d-60
Найти его корни. В ответе указать средний по величине из них.
3
Дано уравнение math.
a4
b-15
c-6
f76
g-72
Найдите кратный корень. В ответе укажите его кратность.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
4
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A11
b10
c14
a4
b7
c65
В ответе указать значение math.
7
Задано уравнение: math
k-2
b-3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,6
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
1,5
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
c2
k?
b-48
x4
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
56
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a10
b4
C?
X05
Y010
В ответе укажите недостающий параметр.
8
Вычислить значение определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-20
Задано характеристическое уравнение: math.
a2
b-20
c62
d-60
Найти его корни. В ответе указать наибольший из них.
5
Дано уравнение math.
a64
b-224
c136
f96
g32
Найти значение его кратного корня.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
3
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A15
b16
c145
a4
b8
c36
В ответе указать значение math.
9
Задано уравнение: math
k3
b2
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,75
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
2
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
c2
k?
b-48
x4
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
26
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a12
b5
C4
X0?
Y05,25
В ответе укажите недостающий параметр.
3
Вычислить значение производной определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a115
b114
c112
a126
b127
c128
a213
b218
c213
a228
b223
c222
-71
Найти уравнение вида: math , которому удовлетворят следующие три корня:
1
3
2
В ответе указать значение math.
-6
Дано уравнение math.
a64
b-224
c136
f96
g32
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
2
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где (x+) и (y+) постоянные величины.
A15
b16
c145
A4
B8
C36
В ответе указать значение math.
0
Задано уравнение: math
k6
b7
c-4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
0,5
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
3
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
c2
d?
k26
b-47
x4
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
1
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a4
b1
C2
X03
Y0?
В ответе укажите недостающий параметр.
2,75
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a115
b117
a122
b123
a131
b132
a219
b212
a224
b223
a237
b231
a314
b313
a322
b324
a331
b337
-10
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
1
3
2
В ответе указать значение math.
11
Дано уравнение math.
a64
b-224
c136
f96
g32
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение r.
-0,25
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение А.
5
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
4
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A14,3
b12,7
c123,2
a3,2
b2,5
c20,7
В ответе указать значение math.
1
Задано уравнение: math
k4
b6
c8
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,5
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
4
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a3
c2
d?
k26
b-47
x4
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
57
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\sin(p)\\ y=b\sin(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b2
C?
X06
Y04,5
В ответе укажите недостающий параметр.
3
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a115
b117
a122
b123
a131
b132
a219
b212
a224
b223
a237
b231
a314
b313
a322
b324
a331
b337
-68
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
1
3
2
В ответе указать значение math.
-6
Дано уравнение math.
a64
b-224
c136
f96
g32
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение math.
0,25
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-9
b26
c-24
A6
B16
C46
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a-1
b6
c-8
d-67
f94
k3
G5
H16
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение В.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b83
c-126
A-378
B-172
F9
G44
H198
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
3
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A14,3
b12,7
c123,2
a3,2
b2,5
c20,7
В ответе указать значение math.
7
Задано уравнение: math
k5
b-3
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-2,25
Задано уравнение вида: math
k1,5
n4
m3
l2
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию math.
-10,8
Найти производную функции math
(1) math
(2) math
(3) math
(4) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a?
d3
k8
b-5
x2
Определить значение недостающего в таблице параметра. В ответе укажите значение этого параметра.
2
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b1
C4
X04
Y0?
В ответе укажите недостающий параметр.
4,5
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
11
Найти корни характеристического уравнения: math. В ответе указать наименьший из корней.
a-2
b3
c2
-0,5
Дано уравнение math.
a3
b-9
c2
f4
g8
Найти значение его кратного корня.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-2
b3
c2
A6
B7
Убедитесь, что общее решение однородного уравнения имеет вид: math. v – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задано неоднородное линейное дифференциальное уравнение: math
a2
b-4
c-6
D30
F-24
K14
K22
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение A.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
4
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: mathНайти замену переменных math math где math и math постоянные величины.
A17
b19
c159
a3
b6
c36
В ответе указать значение math.
2
Задано уравнение: math
k2
b3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,6
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
-2
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a?
d3
k8
b-5
x2
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
11
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a6
b2
C5
X03
Y0?
В ответе укажите недостающий параметр.
6
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}x^2+b_{11}x+c_{11} & a_{21}x^2+b_{21}x+c_{21} \\ a_{12}x^2+b_{12}x+c_{12} & a_{22}x^2+b_{22}x+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
-49
Найти корни характеристического уравнения: math. В ответе указать наибольший из корней.
a-2
b3
c2
2
Дано уравнение math.
a3
b-9
c2
f4
g8
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B.
a-2
b3
c2
A6
B7
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
4
Задано неоднородное линейное дифференциальное уравнение: math
a2
b-4
c-6
D30
F-24
K14
K22
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение B.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
5
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A17
b19
c159
a3
b6
c36
В ответе указать значение math.
5
Задано уравнение: math
k-3
b3
c2
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-2,5
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
-10
Найти производную функции math
(1) math
(2) math
(3) math
(4) math
(5) math
(6) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a?
d3
k8
b-5
x2
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
8
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b4
C5
X05
Y0?
В ответе укажите недостающий параметр.
7,5
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
11
Задано характеристическое уравнение: math.
a3
b-33
c93
d-63
Найти его корни. В ответе указать наименьший из них.
1
Дано уравнение math.
a3
b-9
c-18
f84
g-72
Найти значение его кратного корня.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
-1
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
8
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A12
b15
c12
a6
b3
c6
В ответе указать значение math.
1
Задано уравнение: math
k-2
b-3
c-5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,6
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
8
Найти производную функции math
(1) math>
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k14
b-8
x2
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
6
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a2
b7
C?
X01
Y07,5
В ответе укажите недостающий параметр.
4
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}\sin(x)+b_{11}x+c_{11} & a_{21}\sin(x)+b_{21}x+c_{21} \\ a_{12}\sin(x)+b_{12}x+c_{12} & a_{22}\sin(x)+b_{22}x+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
-55
Задано характеристическое уравнение: math.
a3
b-33
c93
d-63
Найти его корни. В ответе указать средний по величине из них.
3
Дано уравнение math.
a3
b-9
c-18
f84
g-72
Найдите кратный корень. В ответе укажите его кратность.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math– нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
5
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где (x+) и (y+) постоянные величины.
A12
b15
c12
a6
b3
c6
В ответе указать значение math.
0
Задано уравнение: math
k-2
b-3
c5
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-1,4
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
3,5
math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k14
b-8
x2
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
20
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a10
b4
C8
X0?
Y010
В ответе укажите недостающий параметр.
5
Вычислить значение определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
11
Задано характеристическое уравнение: math.
a3
b-33
c93
d-63
Найти его корни. В ответе указать наибольший из них.
7
Дано уравнение math.
a5
b-22
c29
f-120
g288
Найти значение его кратного корня.
3
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
5
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
4
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
6
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A15
b17
c198
a9
b2
c28
В ответе указать значение math.
0
Задано уравнение: math
k3
b2
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,25
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
2
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c?
k14
b-8
x2
Определить значение недостающего в таблице параметра. В ответе укажите значение производной функций в этой точке.
14
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a12
b5
C?
X03
Y05,25
В ответе укажите недостающий параметр.
4
Вычислить значение производной определителя Вронского для x=1. W(x)=\left|\begin{matrix} b_{11}\ln(x)+c_{11} & b_{21}\ln(x)+c_{21} \\ b_{12}\ln(x)+c_{12} & b_{22}\ln(x)+c_{22}\\ \end{matrix}\right|
a111
b112
c117
a125
b128
c123
a219
b213
c218
a228
b222
c225
-49
Найти уравнение вида: math , которому удовлетворят следующие три корня:
3
5
2
В ответе указать значение math.
-10
Дано уравнение math.
a5
b-22
c29
f-120
g288
Найдите кратный корень. В ответе укажите его кратность.
2
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. math – нумеруются в порядке возрастания. В ответе указать значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
4
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A15
b17
c198
a9
b2
c28
В ответе указать значение math.
14
Задано уравнение: math
k6
b7
c-4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-2,5
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
3
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c6
d3
k14
b?
x2
Определить значение недостающего в таблице параметра. В ответе укажите его значение.
-5
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a?
b1
C2
X03
Y02,75
В ответе укажите недостающий параметр.
4
Вычислить значение определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a112
b111
a122
b124
a133
b137
a214
b212
a223
b225
a233
b231
a311
b312
a324
b322
a336
b332
9
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
3
5
2
В ответе указать значение math.
31
Дано уравнение math.
a5
b-22
c29
f-120
g288
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение r.
-0,8
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
3
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение А.
1
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
6
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A14,5
b13,9
c140,8
a4,6
b3,1
c35,5
В ответе указать значение math.
3
Задано уравнение: math
k4
b6
c8
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
-0,5
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение math.
4
Найти производную функции math
(1) math
(2) math
(3) math
Известно, что функции math и math являются решениями некоторого дифференциального уравнения при любых значениях x. При некотором значении x они проходят через одну точку, таким образом, что у этих двух решений одна особая точка.
a2
c6
d3
k14
b?
x2
Определить значение недостающего в таблице параметра. В ответе укажите координату y особой точки.
23
Решение дифференциального уравнения задано в параметрической форме: \left\{ \begin{array}{ll} x=a\ln(p)\\ y=b\ln(p)+C \end{array} \right Условие задачи Коши имеет вид: math. Здесь C произвольная константа.
a8
b2
C3
X06
Y0?
В ответе укажите недостающий параметр.
4,5
Вычислить значение производной определителя Вронского для x=0. W(x)=\left|\begin{matrix} a_{11}+b_{11}x & a_{12}+b_{12}x& a_{13}+b_{13}x \\ a_{21}+b_{21} x& a_{22}+b_{22}x& a_{23}+b_{23}x \\ a_{31}+b_{31}x & a_{32}+b_{32}x& a_{33}+b_{33}x \end{matrix}\right|
a112
b111
a122
b124
a133
b137
a214
b212
a223
b225
a233
b231
a311
b312
a324
b322
a336
b332
54
Найти уравнение вида: math. , которому удовлетворят следующие три корня:
3
5
2
В ответе указать значение math.
-30
Дано уравнение math.
a5
b-22
c29
f-120
g288
Найти значения пары комплексно-сопряжённых корней: math. В ответе указать значение math.
2,4
Найти первообразную функции (неопределённый интеграл) math
(1) math
(2) math
(3) math
Дана задача Коши: y’’’+ay’’+by/+cy=0;\\ y(0)=A;\\ y’(0)=B;\\ y’’’(0)=C.
a-10
b29
c-20
A6
B23
C99
Убедитесь, что общее решение однородного уравнения имеет вид: math. math – нумеруются в порядке возрастания. Решить задачу Коши. В ответе привести значение math.
2
Задана задача Коши для неоднородного линейного дифференциального уравнения: ay’’+by’+cy=d\sin{(kx)}+f\cos{(kx)} y(0)=G; y’(0)=H.
a2
b-4
c-6
d58
f-244
k4
G6
H2
Показать, что общее решение уравнения имеет вид: math. В ответе указать значение В.
6
Задана задача Коши для неоднородного линейного дифференциального уравнения: x^3y’’’+ax^2y’’+bxy’+cy=A+Bx\\ y(0)=F;\\ y’(0)=G;\\ y’’(0)=H.
a4
b94
c-160
A-800
B-396
F15
G82
H404
Показать, что решение задачи имеет вид: math math – нумеруются в порядке возрастания. В ответе привести значение math.
5
Найдите общее решение дифференциального уравнения: math
(1) math
(2) math
(3) math
Задано уравнение вида: math Найти замену переменных math math где math и math постоянные величины.
A14,5
b13,9
c140,8
a4,6
b3,1
c35,5
В ответе указать значение math.
7
Задано уравнение: math
k5
b-3
c4
Показать, что интегрирующий множитель имеет вид: math В ответе указать значение m.
0,25
Задано уравнение вида: math
k3,5
n3
m5
l4
Показать, что общее решение имеет вид: math Где C – произвольная постоянная. В ответе указать значение C, соответствующее начальному условию math.
4