Аналитическая геометрия - ответы на тесты Интуит
Все ответы: Курс знакомит с основными понятиями аналитической геометрии и возможностями использования их на практике.
Даны две матрицы.
Найти их сумму.



 и
и  , если
, если
Заданы координаты двух векторов: (6;9) и (3;2). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Условия.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:



Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Условия.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
 и
и  .Составить уравнение прямой, проходящей через точку
.Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 






Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость ХОУ.
 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 






Задано уравнение эллипса:
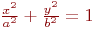
Значения  и
и 
Какая из нижеприведенных точек лежит на этой кривой.



 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
вправо на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
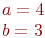 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. есть точка
есть точка  . Выберите правильный вариант уравнения этой гиперболы.
. Выберите правильный вариант уравнения этой гиперболы.




Задано уравнение кривой в виде: 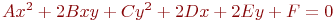 . Найти преобразование координат
. Найти преобразование координат 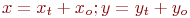 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
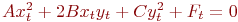 . Указать значение
. Указать значение 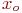 .
.
Ответ введите с точностью 2 знака после запятой.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы . Выберите правильный вариант уравнения этого эллипса после переноса.
вправо на 2 единицы . Выберите правильный вариант уравнения этого эллипса после переноса.




Найти уравнение плоскости в виде  , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
 . Выберите правильный вариант нормального вектора этой плоскости.
. Выберите правильный вариант нормального вектора этой плоскости.




y=kx+b по координатам двух точек, через которые проходит прямая: (4;6) и (5;9).k=3; b=-6 k=-0,8; b=9,4 k=1,25; b=-4,25 k=2; b=-2 Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
 ,
,  .
.





 ,
,  .
.





Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
 ,
,  .
.




 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Отметьте точки, которые не лежат на прямой
. Отметьте точки, которые не лежат на прямой  :
:





Найти решение системы уравнений методом Гаусса.
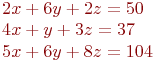
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 x=2; y=3; z=5 x=3; y=5; z=8 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 2 | 6 | 0 | 1 | 72 |
| 1 | -3 | -6 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 0 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.

Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
Найти их разность.
 , если
, если
Заданы координаты двух векторов: (6;9) и (3;2). Найти разность векторов.
Даны два вектора.
Найти угол между ними (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Условия.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 , одна из вершин которого имеет координаты
, одна из вершин которого имеет координаты  , сторона, содержащая точку А, перпендикулярна прямой, заданной уравнением
, сторона, содержащая точку А, перпендикулярна прямой, заданной уравнением  ,на которой лежит другая сторона, угол
,на которой лежит другая сторона, угол  - прямой. Найти координаты точки
- прямой. Найти координаты точки  .
.





Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость УОZ.
Задано уравнение эллипса:
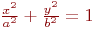
Значения  и
и 
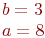
Какая из нижеприведенных точек лежит внутри этой кривой.



 определяет окружность. При каких из приведенных ниже значений
определяет окружность. При каких из приведенных ниже значений  это верно?
это верно?





Даны полуоси гиперболы  и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
 является уравнением гиперболы. При каких из приведенных ниже значений фокального расстояния этой гиперболы это верно?
является уравнением гиперболы. При каких из приведенных ниже значений фокального расстояния этой гиперболы это верно?




Задано уравнение кривой в виде: 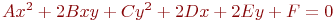 . Найти преобразование координат
. Найти преобразование координат 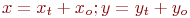 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
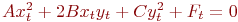 . Указать значение
. Указать значение 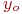 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.
вправо на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.




Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
 и
и  , которые принадлежат нормальному вектору плоскости. Одна из точек также принадлежит плоскости. Выберите правильные варианты уравнения плоскости
, которые принадлежат нормальному вектору плоскости. Одна из точек также принадлежит плоскости. Выберите правильные варианты уравнения плоскости




Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
Rx=1; Ry=3 Rx=5; Ry=-4 Rx=4; Ry=5 Найти угол, под которым с плоскостью
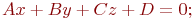
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
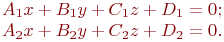
 ,
,  .
.





 ,
,  .
.





Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
 .
.





 , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 , точки
, точки  и
и  . Отметьте точку, которая лежит на прямой
. Отметьте точку, которая лежит на прямой  и расположена между точками
и расположена между точками  и
и  :
:





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И столбец свободных членов:
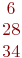
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 6 | 6 | 0 | 1 | 72 |
| 1 | -4 | -9 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.



Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
 , если
, если
Заданы координаты двух векторов: (6;9;7) и (3;2;2). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 . Определить уравнение прямой, пересекающей данную под углом 45 град.
. Определить уравнение прямой, пересекающей данную под углом 45 град.





Заданы координаты точки А(4;5;2). Найти координаты ее проекции на координатную плоскость ZОХ.
Задано уравнение эллипса:
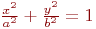
Значения  и
и 
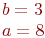
Какая из нижеприведенных точек лежит вне этой кривой.



 – начало координат и расположенная в верхней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в верхней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
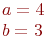 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. , а отношение её полуосей есть 3/4. Выберите правильные варианты уравнения этой гиперболы.
, а отношение её полуосей есть 3/4. Выберите правильные варианты уравнения этой гиперболы.




Задано уравнение кривой в виде: 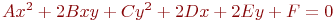 . Найти преобразование координат
. Найти преобразование координат 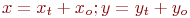 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
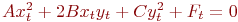 . Указать значение
. Указать значение 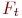 .
.
 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  вправо на 2 единицы. Выберите правильный вариант уравнения этой параболы после переноса.
вправо на 2 единицы. Выберите правильный вариант уравнения этой параболы после переноса.




Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости. Выберите правильный вариант этой плоскости
, которые принадлежат плоскости. Выберите правильный вариант этой плоскости 



Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
a=2; b=-6 a =11,75; b =9,4 a =3,4; b =-4,25 Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
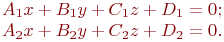 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой. ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в верхней полуплоскости. Ось
– начало координат и расположенная в верхней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Определить точку пресечения прямой
. Определить точку пресечения прямой  с осью
с осью  ?
?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |
| 0 | 7 | 1 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 6 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 8 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.










Дана матрица
Найти обратную матрицу



 , если
, если
Заданы координаты двух векторов: (6;9;7) и (3;2;2). Найти разность векторов.
Найти угол между векторами.
Ответ введите с точностью до 1-го знака после запятой.Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
 . Определите уравнение прямой, содержащей противоположную сторону.
. Определите уравнение прямой, содержащей противоположную сторону.





Заданы координаты точки в полярной системе координат: 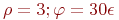 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
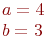 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. проходит через вершину гиперболы. Точка
проходит через вершину гиперболы. Точка  также принадлежит этой гиперболе. Выберите правильный вариант уравнения этой гиперболы.
также принадлежит этой гиперболе. Выберите правильный вариант уравнения этой гиперболы.




Задано уравнение кривой в виде: 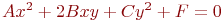 . Найти преобразование координат
. Найти преобразование координат 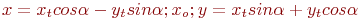 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
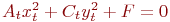 . Указать значение
. Указать значение 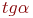 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.




Найти угол между плоскостью заданной уравнением 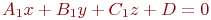 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 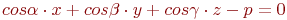
 и
и  , вектор
, вектор  , которые принадлежат плоскости. Выберите правильный вариант этой плоскости
, которые принадлежат плоскости. Выберите правильный вариант этой плоскости



Даны отрезки отсекаемые прямой на осях координат: a=1; b=-2. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





Дан эллиптический параболоид. Определить какие точки ему принадлежат.
 параллельно прямой
параллельно прямой  .
.




 и точка
и точка  . Выберите правильный вариант уравнения касательной к этой параболе в точке
. Выберите правильный вариант уравнения касательной к этой параболе в точке 





 и прямая
и прямая  . Выбрать правильный ответ –
. Выбрать правильный ответ –  и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  не пересекаются
не пересекаются Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 7 | 2 | 2 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 2.5 | 0 | 0 | 42 | 52.5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Даны две матрицы
Найти их сумму.
 , если
, если
Даны координаты трех векторов 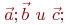 найти коэффициенты в выражении
найти коэффициенты в выражении 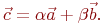
Найти векторное произведение.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 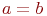 .
.
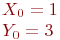
 и
и  . Отметьте уравнения прямых, содержащих его стороны.
. Отметьте уравнения прямых, содержащих его стороны.





Заданы координаты точки в декартовой системе координат (3;4). Найти ее координаты в полярной системе координат.




Задано параметрически уравнение эллипса:
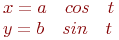
Значения  и
и 
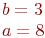
Какая из нижеприведенных точек лежит внутри этой кривой.



 . Выберите правильный вариант точки расположения фокусов данного эллипса
. Выберите правильный вариант точки расположения фокусов данного эллипса 





Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
 является уравнением гиперболы. Выберите правильный вариант значения её полуоси
является уравнением гиперболы. Выберите правильный вариант значения её полуоси




Задано уравнение кривой в виде: 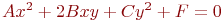 . Найти преобразование координат
. Найти преобразование координат 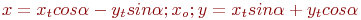 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
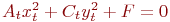 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 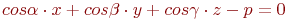 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 ,
,  и
и  , которые принадлежат плоскости. Выберите правильный вариант этой плоскости
, которые принадлежат плоскости. Выберите правильный вариант этой плоскости 




Даны отрезки, отсекаемые прямой на осях координат: a=1; b=-2. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
, 






Дан гиперболический параболоид. Определить какие точки ему принадлежат.
 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  .. Выберите правильный вариант плоскости, содержащей прямую пересечения плоскостей
.. Выберите правильный вариант плоскости, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  . Выберите правильный вариант плоскости
. Выберите правильный вариант плоскости




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Определите, может ли быть вершиной образованного треугольника точка
образуют треугольник. Определите, может ли быть вершиной образованного треугольника точка 





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
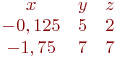
И одно из базисных решений:
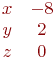
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 15 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их разность.
 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





Даны координаты двух векторов 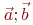 и коэффициенты в выражении
и коэффициенты в выражении 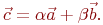
Найти квадрат площади параллелограмма построенного на векторах.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 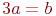 .
.
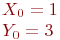
 . Одна из его вершин имеет координаты
. Одна из его вершин имеет координаты  , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты остальных вершин ромба.
. Определить координаты остальных вершин ромба.





Заданы координаты точки в декартовой системе координат (4;3;12). Найти ее координаты в цилиндрической системе координат.



Задано параметрически уравнение эллипса:
Значения  и
и 
Какая из нижеприведенных точек лежит на этой кривой.



 , проходящего через точку
, проходящего через точку  . При каких значениях a это возможно?
. При каких значениях a это возможно?





Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой. – начало координат и расположенная в верхней полуплоскости. Ось
– начало координат и расположенная в верхней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





Задано уравнение кривой в виде: 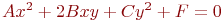 . Найти преобразование координат
. Найти преобразование координат 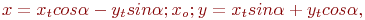 которое приводит уравнение к виду:
которое приводит уравнение к виду:
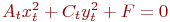 . Указать значение
. Указать значение 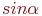 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 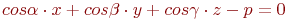 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  и
и  . Выберите правильный вариант плоскости
. Выберите правильный вариант плоскости 





Даны отрезки, отсекаемые прямой на осях координат: a=1; b=-2. Найти координаты точки принадлежащей прямой: (5;…).
Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
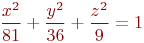
 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 . Чему равна площадь треугольника, образованного точками
. Чему равна площадь треугольника, образованного точками  ,
,  и
и  –выберите правильный вариант
–выберите правильный вариант





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
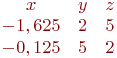
И одно из базисных решений:
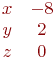
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 0 | 15 | |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 2 | 3 | 4 | 0 | 0 | 0 | 1 | 64 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица.Даны координаты четырех векторов 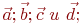 найти коэффициенты в выражении
найти коэффициенты в выражении 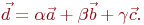
Найти квадрат площади треугольника построенного на векторах.
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 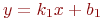 .
.
Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
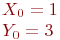
 . Определить уравнения прямых, проходящих на расстоянии 4 от данной, если известно, что соотношение между угловыми коэффициентами этих прямых
. Определить уравнения прямых, проходящих на расстоянии 4 от данной, если известно, что соотношение между угловыми коэффициентами этих прямых  .
.





Заданы координаты точки в декартовой системе координат (8,5;8,5;8,5). Найти ее координаты в сферической системе.



 и
и  . Определите уравнение прямой
. Определите уравнение прямой  , зная, что
, зная, что  – медиана,
– медиана,  .
.





Задано уравнение гиперболы:
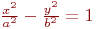
Значения  и
и 
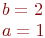
Какая из нижеприведенных точек лежит на этой кривой.
 , проходящего через точки
, проходящего через точки  . При каком значении
. При каком значении  это возможно?
это возможно?Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
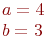
 . Выберите правильный вариант уравнения вышеуказанной линии
. Выберите правильный вариант уравнения вышеуказанной линии




Задано уравнение кривой в виде: Ax2+2Bxy+Cy2+F=0. Найти преобразование координат 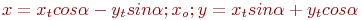 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
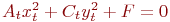 . Указать значение
. Указать значение 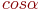 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 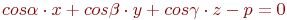 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 и
и  . Выберите правильный вариант плоскости, которая им перпендикулярна и имеет точку
. Выберите правильный вариант плоскости, которая им перпендикулярна и имеет точку 





Через точку с координатами (3;9) проходит пряма, направляющий вектор которой равен (5;4). Найти коэффициенты уравнения этой прямой: y=kx+b.
k=0,8; b=6,6 k=0,25; b=2,5 k=4; b=-1 Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
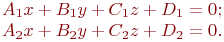
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
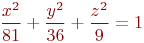
 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Найти уравнение высоты треугольника, образованного точками
. Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  .
.





Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
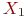 | 20 | 0 | 0 | 10 |
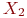 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
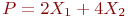
Найти максимальное значение целевой функции.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 2 | 7 | 7 | 1 | 0 | 0 | 0 | 28 | |
| 0 | 6 | 10 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 9 | 7 | 4 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 7 | 2 | 3 | 0 | 0 | 0 | 1 | 64 | |
| 1 | -5 | -8 | -3 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица.Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 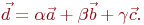 Найти вектор
Найти вектор 
Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 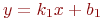 .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
 . Уравнение второй прямой
. Уравнение второй прямой  . Определить площадь прямоугольника со стороной 5, зная, что эта сторона лежит на первой прямой.
. Определить площадь прямоугольника со стороной 5, зная, что эта сторона лежит на первой прямой.





Заданы координаты точки в сферической системе координат: 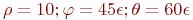 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
 равна 5. Угол при вершине В ромба составляет 60 град. Составьте уравнение прямой
равна 5. Угол при вершине В ромба составляет 60 град. Составьте уравнение прямой  , зная координаты
, зная координаты  .
.





Задано уравнение параболы:
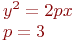
Какая из нижеприведенных точек лежит на этой кривой.



 , проходящего через точку
, проходящего через точку  . Выберите правильный вариант уравнения касательной к данному эллипсу в точке
. Выберите правильный вариант уравнения касательной к данному эллипсу в точке 






Даны полуоси гиперболы  и
и  . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
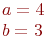



 проходит через фокус параболы. Выберите правильный вариант уравнения вышеуказанной линии
проходит через фокус параболы. Выберите правильный вариант уравнения вышеуказанной линии




Задано уравнение кривой в виде: 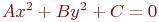 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти угол между плоскостью заданной уравнением 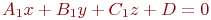 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 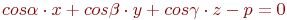 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
 . Выберите правильный вариант плоскости, содержащую их и параллельную оси
. Выберите правильный вариант плоскости, содержащую их и параллельную оси 





Через точку с координатами (3;9) проходит пряма, направляющий вектор которой равен (5;4). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
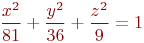
 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 






Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
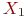 | 20 | 0 | 0 | 10 |
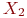 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
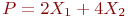
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 5 | 7 | 2 | 0 | 0 | 0 | 1 | 140 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Найти матрицу алгебраических дополнений






Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. . Составьте уравнения прямых, содержащих его стороны., пересекающихся в точке
. Составьте уравнения прямых, содержащих его стороны., пересекающихся в точке  .
.





Уравнение эллипса задано параметрически:
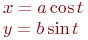
Значения  и
и 
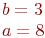
Какая из нижеприведенных точек лежит вне этой кривой?



 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Точка
. Точка  лежит внутри эллипса. При каких значениях
лежит внутри эллипса. При каких значениях  это невозможно?
это невозможно?




 расположена симметрично относительно оси
расположена симметрично относительно оси  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 . Выберите правильный вариант плоскости, содержащую их
. Выберите правильный вариант плоскости, содержащую их




 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.
вправо на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 












 . Одна из вершин имеет координаты
. Одна из вершин имеет координаты  . Определите координаты противоположной вершины.
. Определите координаты противоположной вершины.





 , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается в первом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается в первом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии





 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . Выберите правильный вариант плоскости
. Выберите правильный вариант плоскости




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.










 и
и  . Определите уравнение прямой
. Определите уравнение прямой  , зная, что
, зная, что  – медиана,
– медиана,  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каком из приведенных ниже значении X это верно?
. При каком из приведенных ниже значении X это верно?




 и
и  , вектор
, вектор  .. Выберите правильный вариант плоскости, содержащей прямую пересечения плоскостей
.. Выберите правильный вариант плоскости, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  . Выберите правильный вариант плоскости
. Выберите правильный вариант плоскости




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 равна 5. Угол при вершине В ромба составляет 60 град. Составьте уравнение прямой
равна 5. Угол при вершине В ромба составляет 60 град. Составьте уравнение прямой  , зная координаты
, зная координаты  .
.





 и точка
и точка  . Выберите правильный вариант уравнения касательной к этой параболе в точке
. Выберите правильный вариант уравнения касательной к этой параболе в точке 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












Даны две матрицы.
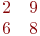
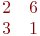
Найти их сумму.



 и
и  , если
, если
Заданы координаты двух векторов: (2;5) и (2;1). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (6;9) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы два уравнения кривых второго порядка:
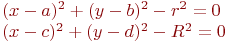
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти тупой угол в градусах между прямой и направлением оси ОХ.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
 и
и  .Составить уравнение прямой, проходящей через точку
.Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 






Заданы координаты точки А(7;8;12). Найти координаты ее проекции на координатную плоскость ХОУ.
 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильные варианты выбора точки
. Отметьте правильные варианты выбора точки 






Задано уравнение эллипса:
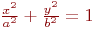
Значения  и
и 
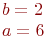
Какая из нижеприведенных точек лежит на этой кривой.



 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  влево на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
влево на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
 равно 2. Выберите правильный вариант уравнения этой гиперболы.
равно 2. Выберите правильный вариант уравнения этой гиперболы.




Задано уравнение кривой в виде: 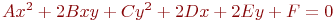 . Найти преобразование координат
. Найти преобразование координат 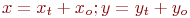 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
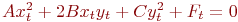 . Указать значение
. Указать значение 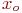 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  влево на 2 единицы . Выберите правильный вариант уравнения этого эллипса после переноса.
влево на 2 единицы . Выберите правильный вариант уравнения этого эллипса после переноса.




Найти уравнение плоскости в виде , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
 и точка
и точка  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?





Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (3;7) и (8;3).
k=2; b=-2 k=-0,8; b=9,4 k=1,25; b=-4,25 Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
 ,
,  .
.





 ,
,  .
.





Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
 ,
,  .
.




 , а полюс - с началом координат. Дана окружность с радиусом 2 с центром
, а полюс - с началом координат. Дана окружность с радиусом 2 с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Отметьте точки, которые лежат на прямой
. Отметьте точки, которые лежат на прямой  :
:





Найти решение системы уравнений методом Гаусса.
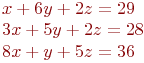
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 x=1; y=3; z=5 x=3; y=3; z=8 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 3 | 1 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 96 |
| 1 | -4 | -8 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 0 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.

Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
Найти их разность.
 , если
, если
Заданы координаты двух векторов: (2;5) и (2;1). Найти разность векторов.
Даны два вектора.
Найти угол между ними (в градусах).
(6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 , одна из вершин которого имеет координаты
, одна из вершин которого имеет координаты  , а катет лежит на прямой, заданной уравнением
, а катет лежит на прямой, заданной уравнением  . Составить уравнения, содержащие две другие стороны этого треугольника, если известно, что длина
. Составить уравнения, содержащие две другие стороны этого треугольника, если известно, что длина  .
.





Заданы координаты точки А(4;3;4). Найти координаты ее проекции на координатную плоскость УОZ.
Задано уравнение эллипса:
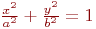
Значения  и
и 
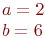
Какая из нижеприведенных точек лежит внутри этой кривой.



 определяет окружность. При каких из приведенных ниже значений
определяет окружность. При каких из приведенных ниже значений  это не верно?
это не верно?





Даны полуоси гиперболы 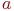 и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
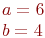 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. является уравнением гиперболы. При каких из приведенных ниже значений эксцентриситета этой гиперболы это верно?
является уравнением гиперболы. При каких из приведенных ниже значений эксцентриситета этой гиперболы это верно?




Задано уравнение кривой в виде: 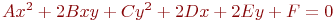 . Найти преобразование координат
. Найти преобразование координат 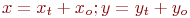 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
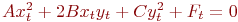 . Указать значение
. Указать значение 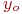 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  влево на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.
влево на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.




Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
 и
и  , которые принадлежат нормальному вектору плоскости
, которые принадлежат нормальному вектору плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?




Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
Rx=1; Ry=2 Rx=5; Ry=-4 Rx=4; Ry=5 Найти угол, под которым с плоскостью
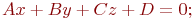
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 ,
,  .
.





 ,
,  .
.





Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
 .
.





 , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 , точки
, точки  и
и  . Отметьте точку, которая лежит на прямой
. Отметьте точку, которая лежит на прямой  и расположена вне отрезка
и расположена вне отрезка  :
:





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И столбец свободных членов:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 6 | 5 | 0 | 1 | 96 |
| 1 | -1 | -7 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
 , если
, если
Заданы координаты двух векторов: (2;5;7) и (2;1;2). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 . Определить уравнение прямой, пересекающей данную под углом 30 град.
. Определить уравнение прямой, пересекающей данную под углом 30 град.





Заданы координаты точки А(4;5;3). Найти координаты ее проекции на координатную плоскость ZОХ.
Задано уравнение эллипса:
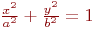
Значения  и
и 
Какая из нижеприведенных точек лежит вне этой кривой.




 – начало координат и расположенная в нижней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в нижней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
 является уравнением гиперболы. Фокус гиперболы есть точка
является уравнением гиперболы. Фокус гиперболы есть точка  , а отношение её полуосей есть 3/4. При каких из приведенных ниже значений
, а отношение её полуосей есть 3/4. При каких из приведенных ниже значений  это верно?
это верно?




Задано уравнение кривой в виде: 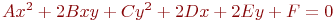 . Найти преобразование координат
. Найти преобразование координат 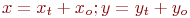 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
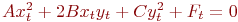 . Указать значение
. Указать значение 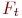 .
.
 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  влева на 2 единицы. Выберите правильный вариант уравнения этой параболы после переноса.
влева на 2 единицы. Выберите правильный вариант уравнения этой параболы после переноса.




Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
a=1; b=-2 a =11,75; b =9,4 a =3,4; b =-4,25 Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в нижней полуплоскости. Ось
– начало координат и расположенная в нижней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Определить точку пресечения прямой
. Определить точку пресечения прямой  с осью
с осью  ?
?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 1 | 4 | 1 | 0 | 0 | 10 | |
| 0 | 5 | 7 | 1 | 0 | 0 | 1 | 140 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.










Дана матрица
Найти обратную матрицу



 , если
, если
Заданы координаты двух векторов: (2;5;7) и (2;1;2). Найти разность векторов.
Найти угол между векторами:
Ответ округлить до целого числа градусов.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
 . Определите уравнение прямой, содержащей противоположную сторону.
. Определите уравнение прямой, содержащей противоположную сторону.





Заданы координаты точки в полярной системе координат: 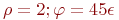 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
 , а полюс - с началом координат. Дана окружность с радиусом 2 с центром
, а полюс - с началом координат. Дана окружность с радиусом 2 с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
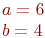 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. и
и  принадлежат гиперболе. Выберите правильный вариант уравнения этой гиперболы.
принадлежат гиперболе. Выберите правильный вариант уравнения этой гиперболы.




Задано уравнение кривой в виде: 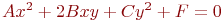 . Найти преобразование координат
. Найти преобразование координат 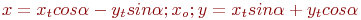 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
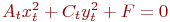 . Указать значение
. Указать значение 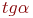 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.




Найти угол между плоскостью заданной уравнением 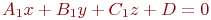 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 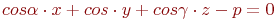
 и
и  , вектор
, вектор  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки отсекаемые прямой на осях координат: a=4; b=4. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
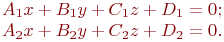
 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





Дан эллиптический параболоид. Определить какие точки ему принадлежат.
 параллельно прямой
параллельно прямой  .
.




 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямая
и прямая  . При каких значениях
. При каких значениях  и
и  прямые
прямые  и
и  не пересекаются
не пересекаются





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 10 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 140 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 2,5 | 0 | 0 | 42 | 52,5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:






Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Даны две матрицы
Найти их сумму.
 , если
, если
Даны координаты трех векторов 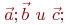 найти коэффициенты в выражении
найти коэффициенты в выражении 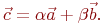
Найти векторное произведение.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения с точностью до второго знака после запятой.
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 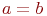 .
.
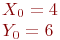
 и
и  составить уравнения прямых, содержащих его стороны.
составить уравнения прямых, содержащих его стороны.





Заданы координаты точки в декартовой системе координат (6;8). Найти ее координаты в полярной системе координат. Укажите угол с точностью до одного знака после запятой.



Задано параметрически уравнение эллипса:
Значения  и
и 
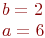
Какая из нижеприведенных точек лежит внутри этой кривой.



 . Выберите правильные варианты точек расположения вершин данного эллипса на оси
. Выберите правильные варианты точек расположения вершин данного эллипса на оси 






Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
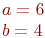 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. является уравнением гиперболы. Точка
является уравнением гиперболы. Точка  является её фокусом. При каких из приведенных ниже значений
является её фокусом. При каких из приведенных ниже значений  это верно?
это верно?




Задано уравнение кривой в виде: 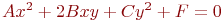 . Найти преобразование координат
. Найти преобразование координат 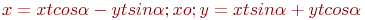 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
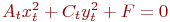 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 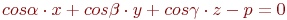 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 ,
,  и
и  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки, отсекаемые прямой на осях координат: a=4; b=4. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
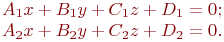 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой. параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
, 






Дан гиперболический параболоид. Определить какие точки ему принадлежат.
 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении 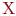 это верно?
это верно?




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Определите, может ли быть вершиной образованного треугольника точка
образуют треугольник. Определите, может ли быть вершиной образованного треугольника точка  при следующем значении
при следующем значении  и
и  -
-




Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
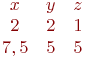
И одно из базисных решений:
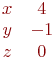
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 25 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 280 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их разность.
 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





Даны координаты трех векторов 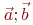 и коэффициенты в выражении
и коэффициенты в выражении 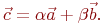 Найти вектор
Найти вектор 
Найти квадрат площади параллелограмма построенного на векторах:
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат. Ответ введите с точностью до 2-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 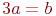 .
.
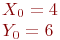
 . Одна из его вершин имеет координаты
. Одна из его вершин имеет координаты  , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты остальных вершин ромба.
. Определить координаты остальных вершин ромба.





Заданы координаты точки в декартовой системе координат (6;8;12). Найти ее координаты в цилиндрической системе координат.




Задано параметрически уравнение эллипса:
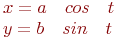
Значения  и
и 
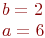
Какая из нижеприведенных точек лежит на этой кривой.



 , проходящего через точку
, проходящего через точку  . При каких значениях b это возможно?
. При каких значениях b это возможно?





Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
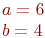 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. – начало координат и расположенная в нижней полуплоскости. Ось
– начало координат и расположенная в нижней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





Задано уравнение кривой в виде: 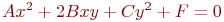 . Найти преобразование координат
. Найти преобразование координат 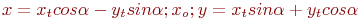 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
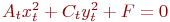 . Указать значение
. Указать значение 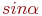 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 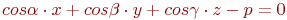 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  и
и  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки, отсекаемые прямой на осях координат: a=4; b=4. Найти координаты точки принадлежащей прямой: (5;…).
Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямым
параллельно прямым  ,
,  .
.




 параллельно прямым
параллельно прямым  ,
,  .
.




Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
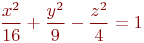
 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.











 . Площадь треугольника, образованного точками
. Площадь треугольника, образованного точками  ,
,  и
и  , равна 2. Какое значение
, равна 2. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
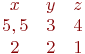
И одно из базисных решений:
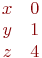
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 0 | 25 | |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 0 | 280 | |
| 0 | 12 | 6 | 7 | 0 | 0 | 0 | 1 | 54 | |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица.Даны координаты четырех векторов 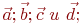 найти коэффициенты в выражении
найти коэффициенты в выражении 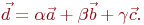
Найти квадрат площади треугольника, построенного на векторах:
Ответ введите с точностью до 1-го знака после запятой.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a=5; вдоль оси ОУ на b=4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 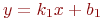 .
.
Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
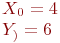
 . Определить уравнения другой прямой, проходящей через точку
. Определить уравнения другой прямой, проходящей через точку  , если известно, что соотношение между угловыми коэффициентами этих прямых
, если известно, что соотношение между угловыми коэффициентами этих прямых  .
.





Заданы координаты точки в декартовой системе координат (3;2;5). Найти ее координаты в сферической системе.



 и
и  определите уравнение прямой
определите уравнение прямой  , зная, что
, зная, что  – медиана,
– медиана,  .
.





Задано уравнение гиперболы:
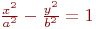
Значения  и
и 
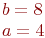
Какая из нижеприведенных точек лежит на этой кривой.





 , проходящего через точки
, проходящего через точки  . При каком значении
. При каком значении  это возможно?
это возможно?Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
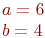
 является уравнением параболы c фокусом в точке
является уравнением параболы c фокусом в точке  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Задано уравнение кривой в виде: 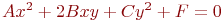 . Найти преобразование координат
. Найти преобразование координат 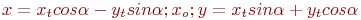 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
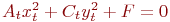 . Указать значение
. Указать значение 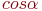 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 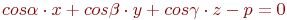 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 и перпендикулярная им
и перпендикулярная им  , которая имеет точку
, которая имеет точку  , При каком из приведенных ниже значении
, При каком из приведенных ниже значении 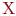 это верно?
это верно?




Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти коэффициенты уравнения этой прямой: y=kx+b.
k=0,8; b=6,6 k=0,25; b=2,5 k=4; b=-1 Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
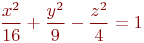
 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Найти уравнение высоты треугольника, образованного точками
. Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  .
.





Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
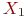 | 20 | 0 | 0 | 10 |
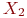 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
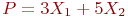 Найти максимум.
Найти максимум.Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 1 | 6 | 5 | 1 | 0 | 0 | 0 | 24 | |
| 0 | 2 | 7 | 3 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 3 | 6 | 2 | 0 | 0 | 1 | 0 | 280 | |
| 0 | 5 | 3 | 4 | 0 | 0 | 0 | 1 | 54 | |
| 1 | -4 | -7 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 32 | 132 | 56 | 32 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 44 | 256 | 42 | 28 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица.Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 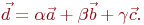 Найти вектор
Найти вектор 
Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 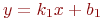 .
.
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
 , а две его вершины имеют координаты
, а две его вершины имеют координаты  . Определить площадь ромба.
. Определить площадь ромба.





Заданы координаты точки в сферической системе координат: 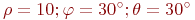 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
 ;
; ;
; )
)  ;
; ;
; )
)  ;
; ;
; )
)  ;
; ;
; )
)  равна 20. Угол при вершине
равна 20. Угол при вершине  ромба составляет 60 град. Составьте уравнение прямой
ромба составляет 60 град. Составьте уравнение прямой  .
.





Задано уравнение параболы:
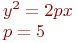
Какая из нижеприведенных точек лежит на этой кривой.



 . Уравнение касательной к данному эллипсу в точке
. Уравнение касательной к данному эллипсу в точке  есть
есть  . При каком значении
. При каком значении  это возможно?
это возможно?Даны полуоси гиперболы  и
и  . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
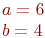



 проходит через фокус параболы
проходит через фокус параболы  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Задано уравнение кривой в виде: 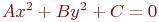 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти острый угол между плоскостью заданной уравнением 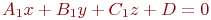 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 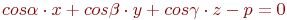 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
 . Выберите правильный вариант плоскости, содержащую их и параллельную оси
. Выберите правильный вариант плоскости, содержащую их и параллельную оси 





Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
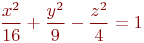
 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Отметьте неправильные варианты выбора точки
. Отметьте неправильные варианты выбора точки 






Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
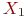 | 20 | 0 | 0 | 10 |
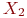 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
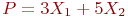
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 6 | 6 | 8 | 1 | 0 | 0 | 0 | 24 | |
| 0 | 5 | 3 | 6 | 0 | 1 | 0 | 0 | 70 | |
| 0 | 6 | 2 | 5 | 0 | 0 | 1 | 0 | 150 | |
| 0 | 8 | 9 | 2 | 0 | 0 | 0 | 1 | 52 | |
| 1 | -3 | -4 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Найти матрицу алгебраических дополнений






Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. задана уравнением
задана уравнением  . Составьте уравнения прямых, содержащих его стороны, зная, что
. Составьте уравнения прямых, содержащих его стороны, зная, что  , а
, а  .
.





Задано параметрически уравнение эллипса:
Значения  и
и 
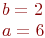
Какая из нижеприведенных точек лежит вне этой кривой.



 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Точка
. Точка  лежит на эллипсе. При каких значениях
лежит на эллипсе. При каких значениях  это невозможно?
это невозможно?




 расположена симметрично относительно оси
расположена симметрично относительно оси  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 При каком из приведенных ниже значении
При каком из приведенных ниже значении  это верно?
это верно?




 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  влево на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.
влево на 2 единицы Выберите правильный вариант уравнения этой гиперболы после переноса.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильные варианты выбора точки
. Отметьте правильные варианты выбора точки 












 . Одна из вершин имеет координаты
. Одна из вершин имеет координаты  . Определите координаты смежных вершин.
. Определите координаты смежных вершин.





 , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается во втором координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается во втором координатном углу. Выберите правильный вариант уравнения вышеуказанной линии






 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этого эллипса после поворота.










 и
и  определите уравнение прямой
определите уравнение прямой  , зная, что
, зная, что  – медиана,
– медиана,  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  и
и  это верно?
это верно?




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.











 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.











 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.











 равна 20. Угол при вершине
равна 20. Угол при вершине  ромба составляет 60 град. Составьте уравнение прямой
ромба составляет 60 град. Составьте уравнение прямой  .
.





 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












Даны две матрицы.
Найти их сумму.
 и
и  , если
, если
Заданы координаты двух векторов: (1;9) и (5;2). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (8;7) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
 и
и  .Составить уравнение прямой, проходящей через точку
.Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 






Заданы координаты точки А(2;4;7). Найти координаты ее проекции на координатную плоскость ХОУ.
 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задано уравнение эллипса:
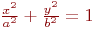
Значения  и
и 
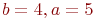
Какая из нижеприведенных точек лежит на этой кривой.





 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вверх на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
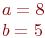 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.




Задано уравнение кривой в виде: 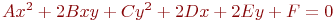 . Найти преобразование координат
. Найти преобразование координат 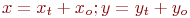 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
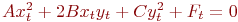 . Указать значение
. Указать значение 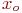 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этого эллипса после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения этого эллипса после переноса.




Найти уравнение плоскости в виде  , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
 и точка
и точка  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?





Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (5;2) и (9;7).
k=2; b=-2 k=-0,8; b=9,4 k=1,25; b=-4,25 Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
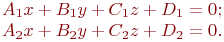
 ,
,  .
.





 ,
,  .
.





Дан эллипсоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит эллипсоиду.
 ,
,  .
.




 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равен
. Чему равен  ?
?Найти решение системы уравнений методом Гаусса.
x=2; y=5; z=8 x=1; y=3; z=5 x=3; y=1; z=1 x=3; y=1; z=5 x=1; y=3; z=8 Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 4 | 1 | 1 | 0 | 5 |
| 0 | 2 | 9 | 0 | 1 | 45 |
| 1 | -4 | -5 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 60 |
 |  |  |  |  |
| 1 | 10 | 0 | 16 | 80 |
 |  |  |  |  |
| 0 | 5 | 0 | 0 | 25 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти главный определитель системы.
Даны две матрицы.
Найти их разность.
 , если
, если
Заданы координаты двух векторов: (1;9) и (5;2). Найти разность векторов.
Даны два вектора.
Найти угол между ними (в градусах).
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти расстояние от прямой до начала координат.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 , а гипотенуза лежит на прямой, заданной уравнением
, а гипотенуза лежит на прямой, заданной уравнением  . Составить уравнение прямой, содержащей сторону
. Составить уравнение прямой, содержащей сторону  этого треугольника, если
этого треугольника, если  .
.





Заданы координаты точки А(7;5;8). Найти координаты ее проекции на координатную плоскость УОZ.
Задано уравнение эллипса:
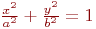
Значения  и
и 
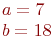
Какая из нижеприведенных точек лежит внутри этой кривой.




 определяет окружность. При каких из приведенных ниже значений
определяет окружность. При каких из приведенных ниже значений  это верно?
это верно?





Даны полуоси гиперболы.  и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
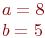 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. является уравнением гиперболы, для которой прямая
является уравнением гиперболы, для которой прямая  является асимптотой. При каких из приведенных ниже значений
является асимптотой. При каких из приведенных ниже значений  это верно?
это верно?




Задано уравнение кривой в виде: 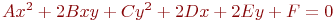 . Найти преобразование координат
. Найти преобразование координат 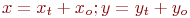 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
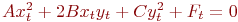 . Указать значение
. Указать значение 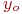 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.




Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
Задано уравнение плоскости в виде  . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
 и
и  , которые принадлежат нормальному вектору плоскости
, которые принадлежат нормальному вектору плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?




Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
Rx=1; Ry=2 Rx=5; Ry=-4 Rx=4; Ry=5 Найти угол, под которым с плоскостью
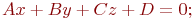
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 ,
,  .
.





 ,
,  .
.





Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
 .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на оси
, а полюс - с началом координат. Эллипс, фокусы которого находятся на оси  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположена между точками
и расположена между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И столбец свободных членов:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  | |
| 0 | 3 | 1 | 1 | 0 | 5 |
| 0 | 6 | 5 | 0 | 1 | 45 |
| 1 | -3 | -7 | 0 | 0 | 0 |
 |  |  |  |  |
| 0 | 10 | 0 | 12 | 90 |
 |  |  |  |  |
| 0 | 10 | 0 | 46 | 70 |
 |  |  |  |  |
| 0 | 5 | 0 | 20 | 35 |
Найти матрицу алгебраических дополнений определителя.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти первый вспомогательный определитель системы.
Даны две матрицы.
Найти их произведение.
 , если
, если
Заданы координаты двух векторов: (1;9;7) и (5;2;2). Найти сумму векторов.
Найти скалярное произведение векторов.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  , и проходящей через точку
, и проходящей через точку  . Считать, что
. Считать, что
 . Определить уравнение прямой, пересекающей данную под углом 15 град.
. Определить уравнение прямой, пересекающей данную под углом 15 град.





Заданы координаты точки А(8;5;5). Найти координаты ее проекции на координатную плоскость ZОХ.
Задано уравнение эллипса:
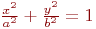
Значения  и
и 
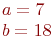
Какая из нижеприведенных точек лежит внутри этой кривой.



 – начало координат и расположенная в правой полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в правой полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
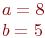 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. является уравнением гиперболы. Фокус гиперболы есть точка
является уравнением гиперболы. Фокус гиперболы есть точка  , а отношение её полуосей есть 3/4. При каких значениях
, а отношение её полуосей есть 3/4. При каких значениях  и
и  это возможно?
это возможно?




Условия.
Задано уравнение кривой в виде: 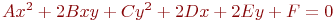 . Найти преобразование координат
. Найти преобразование координат 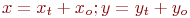 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
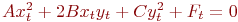 . Указать значение
. Указать значение 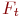 .
.
 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой параболы после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения этой параболы после переноса.




Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение плоскости в виде  . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
a=1; b=-2 a =11,75; b =9,4 a =3,4; b =-4,25 Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
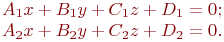 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой. ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





Дан двуполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в правой полуплоскости. Ось
– начало координат и расположенная в правой полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равен
. Чему равен  ?
?Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
И одно из базисных решений:
Найти методом Гаусса базисные решения.
Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 1 | 3 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 4,5 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 8 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
 |  |  |  |  |  |  |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Вычислить определитель.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти второй вспомогательный определитель системы.










Дана матрица
Найти обратную матрицу



 , если
, если
Заданы координаты двух векторов: (1;9;7) и (5;2;2). Найти разность векторов.
Найти угол между векторами.
Ответ введите с округлением до целого.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения прямых в виде  и
и  .
.
Найти расстояние между прямыми. Ответ округлить до второй цифры после запятой.
Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку  . Считать, что
. Считать, что
 . Определите уравнение прямой, содержащей противоположную сторону.
. Определите уравнение прямой, содержащей противоположную сторону.





Заданы координаты точки в полярной системе координат: 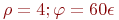 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.
 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
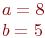 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. и
и  принадлежат гиперболе и её асимптоте соответственно. Выберите правильный вариант уравнения этой гиперболы.
принадлежат гиперболе и её асимптоте соответственно. Выберите правильный вариант уравнения этой гиперболы.




Задано уравнение кривой в виде: 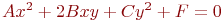 . Найти преобразование координат
. Найти преобразование координат 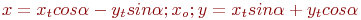 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
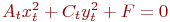 . Указать значение
. Указать значение 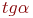 .
.
 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.




Найти острый угол между плоскостью заданной уравнением 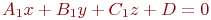 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде  . Найти нормальное уравнение плоскости в виде
. Найти нормальное уравнение плоскости в виде 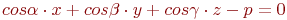


 и
и  , вектор
, вектор  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки отсекаемые прямой на осях координат: a=2; b=7. Найти коэффициенты уравнения прямой : y=kx+b.
k= 2; b=-2 k= -1; b=4 k= -3,5; b=7 Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
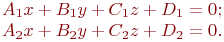
 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 . Найдите значение
. Найдите значение  в точке с координатами:
в точке с координатами:  .
. параллельно прямой
параллельно прямой  .
.




 , уравнение касательной которой в точке
, уравнение касательной которой в точке  ) есть
) есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
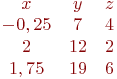
И одно из базисных решений:
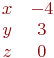
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 5 | 3 | 1 | 0 | 0 | 10 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 2.5 | 0 | 0 | 42 | 52.5 | 20 |
 |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Найти матрицу алгебраических дополнений определителя:






Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Найти решение методом Крамера.
Даны две матрицы
Найти их сумму.
 , если
, если
Даны координаты трех векторов 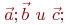 найти коэффициенты в выражении
найти коэффициенты в выражении 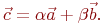
Найти векторное произведение.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Найти угол в градусах между прямой и направлением оси ОХ.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 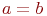 .
.
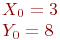
 и
и  . Определить уравнения прямых, содержащих его стороны.
. Определить уравнения прямых, содержащих его стороны.





(8;6). Найти ее координаты в полярной системе координат. В качестве ответа введите угол, округлив его до целого.Задано параметрически уравнение эллипса:
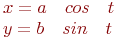
Значения  и
и 
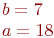
Какая из нижеприведенных точек лежит внутри этой кривой.




 . Выберите правильные варианты точек расположения вершин данного эллипса на оси
. Выберите правильные варианты точек расположения вершин данного эллипса на оси 






Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
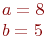 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. является уравнением гиперболы. Выберите правильный вариант значения её эксцентриситета
является уравнением гиперболы. Выберите правильный вариант значения её эксцентриситета




Задано уравнение кривой в виде: 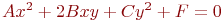 . Найти преобразование координат
. Найти преобразование координат 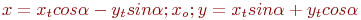 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
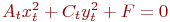 . Указать значение
. Указать значение  в градусах.
в градусах.
Найти уравнение плоскости в виде  , если известны координаты трех точек лежащих в этой плоскости.
, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 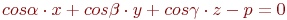 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 ,
,  и
и  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки, отсекаемые прямой на осях координат: a=2; b=7. Найти проекции направляющего вектора.
Rx= 1; Ry=2 Rx= 4; Ry=-4 Rx= 2; Ry=-7 Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
, 






Дан гиперболический параболоид. Определить какие точки ему принадлежат.
 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Точка
образуют треугольник. Точка  – вершинa образованного треугольника. Какое значение
– вершинa образованного треугольника. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
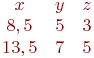
И одно из базисных решений:
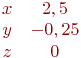
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
 |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
 |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Задана матрица.
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить главный определитель системы.
Даны две матрицы
Найти их разность.
 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





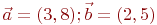 . Найти координаты вектора
. Найти координаты вектора 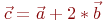 .
.




Найти квадрат площади параллелограмма, построенного на векторах:
После трансляции координаты точки приняли значение (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Задано уравнение прямой в виде  .
.
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что 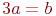 .
.
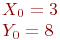
 . Одна из его вершин имеет координаты
. Одна из его вершин имеет координаты  , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты четвертой вершины ромба.
. Определить координаты четвертой вершины ромба.





Заданы координаты точки в декартовой системе координат (8;6;12). Найти ее координаты в цилиндрической системе координат.



Задано параметрически уравнение эллипса:
Значения  и
и 
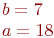
Какая из нижеприведенных точек лежит на этой кривой.



 , проходящего через точку
, проходящего через точку  . При каких значениях c это возможно?
. При каких значениях c это возможно?





Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
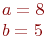 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой. – начало координат и расположенная в правой полуплоскости. Ось
– начало координат и расположенная в правой полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





Задано уравнение кривой в виде: 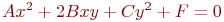 . Найти преобразование координат
. Найти преобразование координат 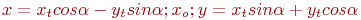 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
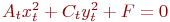 . Указать значение
. Указать значение 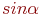 .
.
Найти уравнение плоскости в отрезках, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 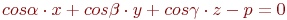 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  C и
C и  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




Даны отрезки, отсекаемые прямой на осях координат: a=2; b=7. Найти координаты точки принадлежащей прямой: (5;…).
Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
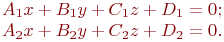
 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
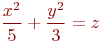
 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 . Площадь треугольника, образованного точками
. Площадь треугольника, образованного точками  ,
,  и
и  , равна 4. Какое значение
, равна 4. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
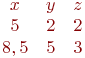
И одно из базисных решений:
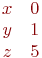
Найти методом Гаусса базисные решения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 0 | 27 | |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 0 | 81 | |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 0 | 160 | |
| 0 | 5 | 7 | 2 | 0 | 0 | 0 | 1 | 140 | |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 80 | 49 | 45 |
 |  |  |  |  |  |  |  |
| 0 | 5 | 0 | 0 | 12 | 105 | 24 | 40 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 54 | 112 | 119 | 27 |
Задана матрица.
Найти матрицу ее алгебраических дополнений
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить первый вспомогательный определитель системы.
Даны две матрицы
Найти их произведение.
 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица.Даны координаты четырех векторов 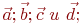 найти коэффициенты в выражении
найти коэффициенты в выражении 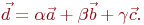
После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде  и
и 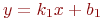 .
.
Угол (в градусах) между прямыми.
Ответ введите с точностью до 1-го знака после запятой.Найти отрезки, отсекаемые на осях координат (b на оси ОХ и b на оси OY) прямой проходящей через точку с координатами  , если известно, что
, если известно, что  .
.
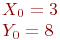
 . Уравнение прямой
. Уравнение прямой  . Определить уравнение второй прямой, проходящей через начало координат.
. Определить уравнение второй прямой, проходящей через начало координат.





Заданы координаты точки в декартовой системе координат (7;4;2). Найти ее координаты в сферической системе.



 и
и  . Составьте уравнение прямой
. Составьте уравнение прямой  , зная, что для
, зная, что для  – медиана,
– медиана,  .
.





Задано уравнение гиперболы:
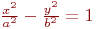
Значения  и
и 
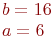
Какая из нижеприведенных точек лежит на этой кривой.




 , проходящего через точки
, проходящего через точки  . При каком значении
. При каком значении  и
и  это возможно?
это возможно?





Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
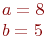
 . Выберите правильный вариант уравнения вышеуказанной линии
. Выберите правильный вариант уравнения вышеуказанной линии




Задано уравнение кривой в виде: 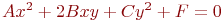 . Найти преобразование координат
. Найти преобразование координат 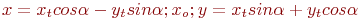 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
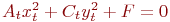 . Указать значение
. Указать значение 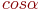 .
.
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
Задано уравнение плоскости в виде 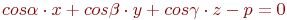 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
 и перпендикулярная им
и перпендикулярная им  , которая имеет точку
, которая имеет точку  , При каком из приведенных ниже значении
, При каком из приведенных ниже значении  это верно?
это верно?




(3;12) проходит пряма, направляющий вектор которой равен (2;7). Найти коэффициенты уравнения этой прямой: y=kx+b.k=0,25; b=6,5 k=0,25; b=2,5 k=3,5; b=1,5 k=3,5; b=0,25 Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
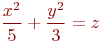
 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Найти уравнение высоты треугольника, образованного точками
. Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  .
.





Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 5 | 3 | 9 | 1 | 0 | 0 | 0 | 6 | |
| 0 | 2 | 3 | 7 | 0 | 1 | 0 | 0 | 8 | |
| 0 | 3 | 4 | 5 | 0 | 0 | 1 | 0 | 9 | |
| 0 | 4 | 6 | 3 | 0 | 0 | 0 | 1 | 13 | |
| 1 | -4 | -5 | -1 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Вычислить ее определитель
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить второй вспомогательный определитель системы.
Задана матрица
Найти обратную матрицу.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица.Заданы три вектора  и коэффициенты в выражении
и коэффициенты в выражении 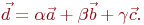 Найти вектор
Найти вектор 
Найти объем параллелепипеда построенного на векторах.
После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:
Найти координаты точек их пересечения, если известны значения коэффициентов:
Заданы уравнения двух прямых в виде 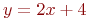 и
и 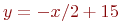 . Найдите угол (в градусах) между прямыми.
. Найдите угол (в градусах) между прямыми.
Заданы уравнения двух пересекающихся прямых:
Найти уравнения биссектрис углов образованных этими прямыми:
Известно, что:
 , а сторона
, а сторона  , определить его площадь.
, определить его площадь.





Заданы координаты точки в сферической системе координат: 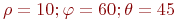 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
 равна
равна  . Угол при вершине
. Угол при вершине  ромба составляет 60 град. Определите координаты
ромба составляет 60 град. Определите координаты  , если
, если  , точка пересечения диагоналей
, точка пересечения диагоналей  ).
).





Задано уравнение параболы:
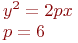
Какая из нижеприведенных точек лежит на этой кривой.



 . Уравнение касательной к данному эллипсу в точке
. Уравнение касательной к данному эллипсу в точке  есть
есть  . При каком значении
. При каком значении  это возможно?
это возможно?Даны полуоси гиперболы 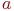 и
и 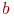 . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.
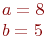



 и
и  принадлежат прямой, которая проходит через фокус параболы. Выберите правильный вариант уравнения вышеуказанной линии
принадлежат прямой, которая проходит через фокус параболы. Выберите правильный вариант уравнения вышеуказанной линии




Задано уравнение кривой в виде: 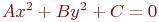 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
a=2; b=4 a=4; b=2 a=5; b=8 Найти угол между плоскостью заданной уравнением 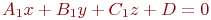 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
Задано уравнение плоскости в виде 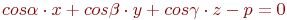 . Найти расстояние до этой плоскости от точки с координатами
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
 . Выберите правильный вариант плоскости, содержащую их и параллельную оси
. Выберите правильный вариант плоскости, содержащую их и параллельную оси 





Через точку с координатами (3;11) проходит прямая, направляющий вектор которой равен (1;4). Найти отрезки, отсекаемые этой прямой на осях координат.
a=-8,25; b=6,6 a=-10; b=2,5 a=0,25; b=-1 Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью эаданной уравнением:
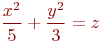
 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
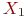 | 20 | 0 | 0 | 10 |
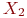 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
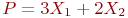
В какой вершине целевая функция достигает максимального значения.



Дана симплекс таблица. Найти решение.
 |  |  |  |  |  |  |  |  | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 0 | 12 | |
| 0 | 8 | 9 | 6 | 0 | 1 | 0 | 0 | 72 | |
| 0 | 4 | 6 | 2 | 0 | 0 | 1 | 0 | 80 | |
| 0 | 7 | 4 | 7 | 0 | 0 | 0 | 1 | 32 | |
| 1 | -1 | -3 | -2 | 0 | 0 | 0 | 0 | 0 |
 |  |  |  |  |  |  |  |
| 0 | 4 | 0 | 0 | 58 | 142 | 16 | 16 |
 |  |  |  |  |  |  |  |
| 0 | 3 | 0 | 0 | 45 | 62 | 20 | 9 |
 |  |  |  |  |  |  |  |
| 0 | 2 | 0 | 0 | 2 | 1 | 1 | 10 |
Задана матрица
Найти матрицу алгебраических дополнений






Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
Вычислить третий вспомогательный определитель системы.
 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. задана уравнением
задана уравнением  . Найдите уравнения прямых, содержащих его стороны, если известны координаты
. Найдите уравнения прямых, содержащих его стороны, если известны координаты  и
и  .
.





Задано параметрически уравнение эллипса:
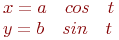
Значения  и
и 
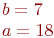
Какая из нижеприведенных точек лежит внутри этой кривой.



 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Точка
. Точка  ) лежит вне эллипса. При каких значениях
) лежит вне эллипса. При каких значениях  это невозможно?
это невозможно?




 принадлежит параболе, расположенной симметрично относительно оси
принадлежит параболе, расположенной симметрично относительно оси  . Выберите правильный вариант уравнения этой
. Выберите правильный вариант уравнения этой 




 . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 . Одна из вершин имеет координаты
. Одна из вершин имеет координаты  . Определите координаты точки пересечения диагоналей прямоугольника, если известна длина стороны
. Определите координаты точки пересечения диагоналей прямоугольника, если известна длина стороны  .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на оси
, а полюс - с началом координат. Эллипс, фокусы которого находятся на оси  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается в третьем координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается в третьем координатном углу. Выберите правильный вариант уравнения вышеуказанной линии





 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.










 и
и  . Составьте уравнение прямой
. Составьте уравнение прямой  , зная, что для
, зная, что для  – медиана,
– медиана,  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 равна
равна  . Угол при вершине
. Угол при вершине  ромба составляет 60 град. Определите координаты
ромба составляет 60 град. Определите координаты  , если
, если  , точка пересечения диагоналей
, точка пересечения диагоналей  ).
).





 , уравнение касательной которой в точке
, уравнение касательной которой в точке  ) есть
) есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  , если
, если
 и
и  .Составить уравнение прямой, содержащей высоту
.Составить уравнение прямой, содержащей высоту  треугольника
треугольника  .
.





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вниз на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
вниз на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





 равна равна 1. Выберите правильные варианты уравнения этой гиперболы
равна равна 1. Выберите правильные варианты уравнения этой гиперболы




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этого эллипса после переноса.
вниз на 3 единицы. Выберите правильный вариант уравнения этого эллипса после переноса.




 и точка
и точка  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?





 ,
,  .
.





 ,
,  .
.





 ,
,  .
.




 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равен
. Чему равен  ?
? , если
, если
 , а a гипотенуза лежит на прямой, заданной уравнением
, а a гипотенуза лежит на прямой, заданной уравнением  . Составить уравнения двух других прямых, содержащих стороны этого треугольника, зная, что длины сторон
. Составить уравнения двух других прямых, содержащих стороны этого треугольника, зная, что длины сторон  и
и  относятся как
относятся как  .
. 





 определяет мнимую окружность. При каком значении
определяет мнимую окружность. При каком значении  это верно?
это верно? является уравнением гиперболы, фокальное расстояния которой равно 20. При каком из приведенных ниже значении
является уравнением гиперболы, фокальное расстояния которой равно 20. При каком из приведенных ниже значении  это верно?
это верно?




 с центром симметрии в точке О(0,0) – начале координат. Затем центр перенесли по оси Оy вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.
с центром симметрии в точке О(0,0) – начале координат. Затем центр перенесли по оси Оy вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса. >
> 



 и
и  , которые принадлежат нормальному вектору плоскости
, которые принадлежат нормальному вектору плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?




 ,
,  .
.





 ,
,  .
.





 .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на оси
, а полюс - с началом координат. Эллипс, фокусы которого находятся на оси  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположена вне отрезка
и расположена вне отрезка  . Какое значение
. Какое значение  из приведенных ниже, удовлетворяет условиям задачи?
из приведенных ниже, удовлетворяет условиям задачи?





 , если
, если
 . Определить уравнение прямой, пересекающей данную под углом 45 град.
. Определить уравнение прямой, пересекающей данную под углом 45 град.





 – начало координат и расположенная в левой полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в левой полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





 , а значение эксцентриситета этой гиперболы равно 1,25. Выберите правильный вариант уравнения этой гиперболы.
, а значение эксцентриситета этой гиперболы равно 1,25. Выберите правильный вариант уравнения этой гиперболы.




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этой параболы после переноса.
вниз на 3 единицы. Выберите правильный вариант уравнения этой параболы после переноса.




 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в левой полуплоскости. Ось
– начало координат и расположенная в левой полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равен
. Чему равен  ?
?









 , если
, если
 . Определите уравнение прямой, содержащей перпендикулярную сторону.
. Определите уравнение прямой, содержащей перпендикулярную сторону.





 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 является уравнением гиперболы, для которой прямая
является уравнением гиперболы, для которой прямая  является асимптотой. При каких из приведенных ниже значений
является асимптотой. При каких из приведенных ниже значений  это верно?
это верно?




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.




 и
и  , вектор
, вектор  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямая
и прямая  . Точка
. Точка  лежит пересечении этих прямых
лежит пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 , если
, если
 :
:  , длины сторон
, длины сторон  ,
,  и
и  . Определить уравнения прямых, содержащих его стороны
. Определить уравнения прямых, содержащих его стороны  и
и  .
.





 . Выберите правильный вариант значения его большой полуоси
. Выберите правильный вариант значения его большой полуоси





 является уравнением гиперболы. Прямая
является уравнением гиперболы. Прямая  параллельна её асимптоте. При каком из приведенных ниже значении
параллельна её асимптоте. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  и
и  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении это верно?
это верно?




 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
, 






 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Точка
образуют треугольник. Точка  – вершинa образованного треугольника. Какое значение
– вершинa образованного треугольника. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





 , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты остальных вершин ромба.
. Определить координаты остальных вершин ромба.





 , проходящего через точку
, проходящего через точку  . При каких значениях
. При каких значениях  и c это возможно?
и c это возможно?





 – начало координат и расположенная в левой полуплоскости. Ось
– начало координат и расположенная в левой полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  и
и  . При каком из приведенных ниже значении C это верно?
. При каком из приведенных ниже значении C это верно?




 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 . Площадь треугольника, образованного точками
. Площадь треугольника, образованного точками  ,
,  и
и  , равна 4. Какие значения
, равна 4. Какие значения  и
и  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица. . Определить уравнения прямой, проходящей через точку
. Определить уравнения прямой, проходящей через точку  , если известно, что соотношение между угловыми коэффициентами этих прямых
, если известно, что соотношение между угловыми коэффициентами этих прямых  .
.





 , зная координату вершины
, зная координату вершины  , если известны координаты вершин треугольника
, если известны координаты вершин треугольника  и
и  .
.





 , проходящего через точки
, проходящего через точки  . При каком значении
. При каком значении  и
и  это возможно?
это возможно?





 является уравнением параболы c директрисой
является уравнением параболы c директрисой  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и перпендикулярная им
и перпендикулярная им  , которая имеет точку
, которая имеет точку  , При каком из приведенных ниже значении
, При каком из приведенных ниже значении  это верно?
это верно?




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. , а точка пересечения диагоналей
, а точка пересечения диагоналей  . Определить его площадь.
. Определить его площадь.





 равна
равна . Угол при вершине
. Угол при вершине  ромба составляет 120 град. Составьте уравнение прямой
ромба составляет 120 град. Составьте уравнение прямой  , лежащей выше оси абсцисс, если
, лежащей выше оси абсцисс, если  .
.





 . Уравнение касательной к данному эллипсу в точке
. Уравнение касательной к данному эллипсу в точке  есть
есть  . При каком значении
. При каком значении  и
и  это возможно?
это возможно?






 . При каком из приведенных ниже значении X это верно?
. При каком из приведенных ниже значении X это верно?









 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. задана уравнением
задана уравнением  . Найдите уравнения его сторон.
. Найдите уравнения его сторон.





 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  .Точка
.Точка  лежит внутри эллипса. При каком значении
лежит внутри эллипса. При каком значении  это возможно?
это возможно?




 принадлежит параболе
принадлежит параболе  , расположенной симметрично относительно оси
, расположенной симметрично относительно оси  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?





 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке О(0,0) – начале координат. Затем центр перенесли по оси Оy вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса.
с центром симметрии в точке О(0,0) – начале координат. Затем центр перенесли по оси Оy вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после переноса. >
> 



 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 . Одна из вершин имеет координаты
. Одна из вершин имеет координаты  . Определите площадь квадрата.
. Определите площадь квадрата. , а полюс - с началом координат. Эллипс, фокусы которого находятся на оси
, а полюс - с началом координат. Эллипс, фокусы которого находятся на оси  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный 0,6. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается в четвертом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается в четвертом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии





 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.










 , зная координату вершины
, зная координату вершины  , если известны координаты вершин треугольника
, если известны координаты вершин треугольника  и
и  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 равна
равна . Угол при вершине
. Угол при вершине  ромба составляет 120 град. Составьте уравнение прямой
ромба составляет 120 град. Составьте уравнение прямой  , лежащей выше оси абсцисс, если
, лежащей выше оси абсцисс, если  .
.





 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  , если
, если
 и
и  , составьте уравнение прямой, проходящей через точку
, составьте уравнение прямой, проходящей через точку  параллельно прямой
параллельно прямой  .
.





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо и по оси
вправо и по оси  вверх на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
вверх на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





 равна равна 2. . При каких из приведенных ниже значений
равна равна 2. . При каких из приведенных ниже значений  это верно?
это верно?




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этого эллипса после двух переносов.
вверх на 3 единицы. Выберите правильный вариант уравнения этого эллипса после двух переносов.




 и точка
и точка  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  точка
точка  принадлежит плоскости?
принадлежит плоскости?





 ,
,  .
.





 ,
,  .
.





 ,
,  .
.




 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равно
. Чему равно  ?
? , если
, если
 , координаты вершины
, координаты вершины  , а противоположная сторона лежит на прямой, заданной уравнением
, а противоположная сторона лежит на прямой, заданной уравнением  . Составить уравнения прямых, содержащих две другие стороны этого треугольника, зная, что
. Составить уравнения прямых, содержащих две другие стороны этого треугольника, зная, что  - катет.
- катет.





 определяет окружность. При каких из приведенных ниже значений
определяет окружность. При каких из приведенных ниже значений  это верно?
это верно?





 является уравнением линии, эксцентриситета которой равен 1,25. При каком из приведенных ниже значении
является уравнением линии, эксцентриситета которой равен 1,25. При каком из приведенных ниже значении  это верно верно для гиперболы?
это верно верно для гиперболы?




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.
вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.




 и
и  , которые принадлежат нормальному вектору плоскости
, которые принадлежат нормальному вектору плоскости  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 ,
,  .
.





 ,
,  .
.





 .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой
, а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса




 . точки
. точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположена между точками
и расположена между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 , если
, если
 . Определить уравнение прямой, пересекающей данную под углом 135 град.
. Определить уравнение прямой, пересекающей данную под углом 135 град.





 – начало координат и расположенная в верхней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в верхней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





 , а значение эксцентриситета этой гиперболы равно 25/9. Выберите правильный вариант уравнения этой гиперболы.
, а значение эксцентриситета этой гиперболы равно 25/9. Выберите правильный вариант уравнения этой гиперболы.




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой параболы после двух переносов.
вверх на 3 единицы. Выберите правильный вариант уравнения этой параболы после двух переносов.




 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в верхней полуплоскости. Ось
– начало координат и расположенная в верхней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
?









 , если
, если
 . Определите уравнение прямой, содержащей противоположную сторону.
. Определите уравнение прямой, содержащей противоположную сторону.





 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 является уравнением гиперболы, где её асимптоте принадлежит точка
является уравнением гиперболы, где её асимптоте принадлежит точка  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.




 и
и  , вектор
, вектор  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 , если
, если
 и
и  . Определить уравнения прямых, содержащих его стороны, лежащих в той же полуплоскости относительно
. Определить уравнения прямых, содержащих его стороны, лежащих в той же полуплоскости относительно  , что и точка
, что и точка  .
.





 . Введите правильный вариант значения его малой полуоси
. Введите правильный вариант значения его малой полуоси является уравнением гиперболы. Прямая
является уравнением гиперболы. Прямая  параллельна её асимптоте. При каких из приведенных ниже значений
параллельна её асимптоте. При каких из приведенных ниже значений  это верно?
это верно?




 , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Точки
образуют треугольник. Точки  и
и  – две вершины образованного треугольника. Определите, является ли третья вершина образованного треугольника точкой пересечения следующих прямых
– две вершины образованного треугольника. Определите, является ли третья вершина образованного треугольника точкой пересечения следующих прямых  и
и 
 и
и 
 и
и 
 и оси
и оси 
 и оси
и оси 
 и оси
и оси 
 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





 со стороной
со стороной  . Одна из его вершин имеет координаты
. Одна из его вершин имеет координаты  , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты вершин квадрата.
. Определить координаты вершин квадрата.





 , проходящего через точку
, проходящего через точку  . При каких значениях
. При каких значениях  и
и  это возможно?
это возможно?





 – начало координат и расположенная в верхней полуплоскости. Ось
– начало координат и расположенная в верхней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  и
и  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой
как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой  . Так же известно, что одна из этих вершин расположена на оси
. Так же известно, что одна из этих вершин расположена на оси  . Чему равна
. Чему равна  координата другой вершины?
координата другой вершины?





 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица. . Составить уравнения прямой, проходящей через точку
. Составить уравнения прямой, проходящей через точку  , если известно, что соотношение между угловыми коэффициентами этих прямых
, если известно, что соотношение между угловыми коэффициентами этих прямых  .
. 





 и
и  . Определите уравнение прямой, содержащей основание
. Определите уравнение прямой, содержащей основание  , зная, что высота
, зная, что высота  проходит через точку
проходит через точку  .
.





 , а полюс - с началом координат. Точки
, а полюс - с началом координат. Точки  лежат на эллипсе. Выберите правильный вариант уравнения этого эллипса
лежат на эллипсе. Выберите правильный вариант уравнения этого эллипса




 и директрисой
и директрисой  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и перпендикулярная им
и перпендикулярная им  , которая имеет точку
, которая имеет точку  , При каких из приведенных ниже значений
, При каких из приведенных ниже значений  и
и  это верно?
это верно?




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. заданы уравнениями
заданы уравнениями  . Определить его площадь.
. Определить его площадь.





 равна 9. Угол при вершине
равна 9. Угол при вершине  ромба составляет 30 град. Уравнение диагонали
ромба составляет 30 град. Уравнение диагонали  . Определите уравнение прямой
. Определите уравнение прямой  .
.





 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Уравнение касательной к данному эллипсу в точке
. Уравнение касательной к данному эллипсу в точке  есть
есть  . При каком значении
. При каком значении  это возможно?
это возможно? – начале координат и параметр, равный 5. Затем вершину перенесли по оси
– начале координат и параметр, равный 5. Затем вершину перенесли по оси  вправо на 5 единиц. Выберите правильный вариант уравнения параболы после переноса.
вправо на 5 единиц. Выберите правильный вариант уравнения параболы после переноса.




 содержит две точки
содержит две точки  и параллельна оси
и параллельна оси  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?











 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. задана уравнением
задана уравнением  . Найдите уравнения прямых, содержащих его стороны.
. Найдите уравнения прямых, содержащих его стороны.





 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Точка
. Точка  лежит на эллипсе. При каком значении
лежит на эллипсе. При каком значении  это возможно?
это возможно? принадлежит параболе, расположенной симметрично относительно оси
принадлежит параболе, расположенной симметрично относительно оси  . Выберите правильный вариант уравнения этой гиперболы.
. Выберите правильный вариант уравнения этой гиперболы.




 . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.
вверх на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 . Его площадь равна
. Его площадь равна  . Определите координаты противоположной вершины, если координаты вершины при основании равны
. Определите координаты противоположной вершины, если координаты вершины при основании равны  .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой
, а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается в первом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается в первом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии





 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули против часовой стрелки на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.










 и
и  . Определите уравнение прямой, содержащей основание
. Определите уравнение прямой, содержащей основание  , зная, что высота
, зная, что высота  проходит через точку
проходит через точку  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  и
и  это верно?
это верно?




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  и параллельной вектору
и параллельной вектору  , есть
, есть  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 и
и  . Найти расстояние
. Найти расстояние  между прямыми
между прямыми





 равна 9. Угол при вершине
равна 9. Угол при вершине  ромба составляет 30 град. Уравнение диагонали
ромба составляет 30 град. Уравнение диагонали  . Определите уравнение прямой
. Определите уравнение прямой  .
.





 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  , если
, если
 и
и  .Составить уравнение прямой, содержащей высоту
.Составить уравнение прямой, содержащей высоту  треугольника
треугольника  .
.





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо и по оси
вправо и по оси  вниз на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.
вниз на 3 единицы. Выберите правильный вариант уравнения окружности после переноса.





 есть точка
есть точка  , а одна из полуосей гиперболы равна 8. При каких из приведенных ниже значений
, а одна из полуосей гиперболы равна 8. При каких из приведенных ниже значений  это верно?
это верно?




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этого эллипса после двух переносов.
вниз на 3 единицы. Выберите правильный вариант уравнения этого эллипса после двух переносов.




 и точка
и точка  , принадлежащая ей. Выберите правильный вариант уравнения плоскости
, принадлежащая ей. Выберите правильный вариант уравнения плоскости




 ,
,  .
.





 ,
,  .
.





 ,
,  .
.




 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равно
. Чему равно  ?
? , если
, если
 , а гипотенуза лежит на прямой, заданной уравнением
, а гипотенуза лежит на прямой, заданной уравнением  . Определить координаты вершины
. Определить координаты вершины  , лежащей в одной полуплоскости с точкой
, лежащей в одной полуплоскости с точкой  , зная уравнение высоты
, зная уравнение высоты  . Угол
. Угол  прямой.
прямой.





 определяет мнимую окружность. При каком значении
определяет мнимую окружность. При каком значении  это верно?
это верно? является уравнением гиперболы, для которой точка
является уравнением гиперболы, для которой точка  является фокусом. При каких из приведенных ниже значений
является фокусом. При каких из приведенных ниже значений  это верно?
это верно?




 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.
вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.




 , которые принадлежат плоскости. Выберите правильный вариант этой плоскости
, которые принадлежат плоскости. Выберите правильный вариант этой плоскости



 ,
,  .
.





 ,
,  .
.





 .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой
, а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса




 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположена вне отрезка
и расположена вне отрезка  . Какое значение
. Какое значение  из приведенных ниже, удовлетворяет условиям задачи?
из приведенных ниже, удовлетворяет условиям задачи?





 , если
, если
 . Определить уравнение прямой, пересекающей данную под углом 90 град.
. Определить уравнение прямой, пересекающей данную под углом 90 град.





 – начало координат и расположенная в нижней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии
– начало координат и расположенная в нижней полуплоскости. Выберите правильный вариант уравнения вышеуказанной линии





 является уравнением гиперболы. Вершина гиперболы есть точка
является уравнением гиперболы. Вершина гиперболы есть точка  . При каком из приведенных ниже значении эксцентриситета этой гиперболы это верно?
. При каком из приведенных ниже значении эксцентриситета этой гиперболы это верно?




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем вершину перенесли по оси
– начале координат. Затем вершину перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этой параболы после двух переносов.
вниз на 3 единицы. Выберите правильный вариант уравнения этой параболы после двух переносов.




 и два вектора
и два вектора  ,
,  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым
 .
.




 – начало координат и расположенная в нижней полуплоскости. Ось
– начало координат и расположенная в нижней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
?









 , если
, если
 , проходящей через точку пересечения его диагоналей. Определите уравнения прямых, содержащих эти стороны квадрата.
, проходящей через точку пересечения его диагоналей. Определите уравнения прямых, содержащих эти стороны квадрата.





 , а полюс - с началом координат. Дана окружность единичного радиуса с центром
, а полюс - с началом координат. Дана окружность единичного радиуса с центром  . Выберите правильные варианты уравнения этой окружности:
. Выберите правильные варианты уравнения этой окружности:





 является уравнением гиперболы. Точка
является уравнением гиперболы. Точка  принадлежит прямой
принадлежит прямой  , которая проходит через вершину гиперболы. При каком из приведенных ниже значении
, которая проходит через вершину гиперболы. При каком из приведенных ниже значении  это верно?
это верно?




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.




 и
и  , вектор \
, вектор \ , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  ,
, и
и  это верно?
это верно?




 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 , если
, если
 , лежащая на прямой
, лежащая на прямой  , равна
, равна  , координаты вершин
, координаты вершин  и
и  . Определить уравнения прямых, содержащих его стороны в той же полуплоскости, что и начало координат.
. Определить уравнения прямых, содержащих его стороны в той же полуплоскости, что и начало координат.





 . Выберите правильный вариант значения его эксцентриситета
. Выберите правильный вариант значения его эксцентриситета





 является уравнением гиперболы. Прямая
является уравнением гиперболы. Прямая  параллельна её асимптоте. При каких из приведенных ниже значений
параллельна её асимптоте. При каких из приведенных ниже значений  и
и  это верно?
это верно?




 ,
,  и
и  , которые принадлежат плоскости
, которые принадлежат плоскости  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  ,
,  и ,
и , это верно?
это верно?




 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 и прямую
и прямую  .
.




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  B и параллельной вектору
B и параллельной вектору  , есть
, есть  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 ,
,  ,
,  . Пересекаясь друг с другом, прямые
. Пересекаясь друг с другом, прямые  ,
,  и
и  образуют треугольник. Точки
образуют треугольник. Точки  и
и  – две вершины образованного треугольника. Определите – будет ли третьей вершиной образованного треугольника являться следующая точка
– две вершины образованного треугольника. Определите – будет ли третьей вершиной образованного треугольника являться следующая точка





 , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





 . Одна из его вершин имеет координаты
. Одна из его вершин имеет координаты  , а две другие лежат на прямой, заданной уравнением
, а две другие лежат на прямой, заданной уравнением  . Определить координаты четвертой вершины ромба.
. Определить координаты четвертой вершины ромба.





 , проходящего через точку
, проходящего через точку  . При каких значениях
. При каких значениях  ,
,  и
и  это возможно?
это возможно?





 – начало координат и расположенная в нижней полуплоскости. Ось
– начало координат и расположенная в нижней полуплоскости. Ось  является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии
является действительной осью симметрии этой гиперболы. Выберите правильный вариант уравнения вышеуказанной линии





 , которая принадлежат плоскости
, которая принадлежат плоскости  , и две параллельные плоскости
, и две параллельные плоскости  и
и  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  это верно?
это верно?




 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой
как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой  , Также известно, что одна из этих вершин расположена на оси
, Также известно, что одна из этих вершин расположена на оси  . Чему равна
. Чему равна  координата другой вершины?
координата другой вершины?





 , если
-(2x3)матрица,
-(3x1)-матрица.
, если
-(2x3)матрица,
-(3x1)-матрица. . Составить уравнения прямой, проходящей через точку
. Составить уравнения прямой, проходящей через точку  , если известно, что соотношение между угловыми коэффициентами этих прямых
, если известно, что соотношение между угловыми коэффициентами этих прямых  .
. 





 и
и  . Определите уравнение прямой
. Определите уравнение прямой  , зная, что высота
, зная, что высота  проходит через точку
проходит через точку  и что
и что  .
.





 , а полюс - с началом координат. Точки
, а полюс - с началом координат. Точки  лежат на эллипсе. Выберите правильный вариант уравнения этого эллипса
лежат на эллипсе. Выберите правильный вариант уравнения этого эллипса




 и директрисой
и директрисой  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и перпендикулярная им
и перпендикулярная им  , которая имеет точку
, которая имеет точку  , При каких из приведенных ниже значений
, При каких из приведенных ниже значений  и
и  это верно?
это верно?




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и
и 





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  и
и  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. , а длина диагонали
, а длина диагонали  .Определить его площадь, если известно, что сторона
.Определить его площадь, если известно, что сторона  .
.





 равна
равна  . Тангенс половины угла при вершине
. Тангенс половины угла при вершине  ромба составляет 3/11. Составьте уравнения прямой
ромба составляет 3/11. Составьте уравнения прямой  .
.





 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Уравнение касательной к данному эллипсу в точке
. Уравнение касательной к данному эллипсу в точке  есть
есть  . При каком значении
. При каком значении  это возможно?
это возможно? – начале координат и параметр, равный 7. Затем вершину перенесли по оси
– начале координат и параметр, равный 7. Затем вершину перенесли по оси  влево на 7 единиц. Выберите правильный вариант уравнения параболы после переноса.
влево на 7 единиц. Выберите правильный вариант уравнения параболы после переноса.




 содержит две точки
содержит две точки  и параллельна оси
и параллельна оси  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и пересекающей две прямые
и пересекающей две прямые  и
и





 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и
и  . Точка
. Точка  лежит на биссектрисе между прямыми
лежит на биссектрисе между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 , если
-(2x2)матрица,
-(2x2)-матрица.
, если
-(2x2)матрица,
-(2x2)-матрица. задана уравнением
задана уравнением  . Найдите уравнения прямых, содержащих его стороны.
. Найдите уравнения прямых, содержащих его стороны.





 , а полюс - с началом координат. Дано уравнение эллипса
, а полюс - с началом координат. Дано уравнение эллипса  . Точка
. Точка  лежит вне эллипса. При каких значениях
лежит вне эллипса. При каких значениях  это возможно?
это возможно?




 принадлежит параболе
принадлежит параболе  , расположенной симметрично относительно оси
, расположенной симметрично относительно оси  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 и прямую
и прямую  ,
,  ,
, 






 и прямую
и прямую  ,
,  ,
, 






 и
и 





 с центром симметрии в точке
с центром симметрии в точке  – начале координат. Затем центр перенесли по оси
– начале координат. Затем центр перенесли по оси  вправо на 2 единицы и по оси
вправо на 2 единицы и по оси  вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.
вниз на 3 единицы. Выберите правильный вариант уравнения этой гиперболы после двух переносов.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?











 . Точка пересечения диагоналей имеет координаты
. Точка пересечения диагоналей имеет координаты  . Определите координаты вершин
. Определите координаты вершин  и
и  , зная длину стороны ромба
, зная длину стороны ромба  .
.





 , а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой
, а полюс - с началом координат. Эллипс, фокусы которого находятся на прямой  , проходит через точку
, проходит через точку  и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса
и имеет эксцентриситет, равный нулю. Выберите правильный вариант уравнения этого эллипса




 – начале координат и с параметром, равным 8, располагается в четвертом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии
– начале координат и с параметром, равным 8, располагается в четвертом координатном углу. Выберите правильный вариант уравнения вышеуказанной линии





 и отсекающую на координатных осях положительные отрезки длиной
и отсекающую на координатных осях положительные отрезки длиной  и
и  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 параллельно прямой
параллельно прямой  .
.




 с её вершиной в точке
с её вершиной в точке  – начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.
– начале координат. Затем cистему координат повернули по часовой стрелке на 90 градусов. Выберите правильный вариант уравнения этой гиперболы после поворота.










 и
и  . Определите уравнение прямой
. Определите уравнение прямой  , зная, что высота
, зная, что высота  проходит через точку
проходит через точку  и что
и что  .
.





 и прямая
и прямая  , её пересекающая в точке
, её пересекающая в точке  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  это верно?
это верно?




 и
и  , вектор
, вектор  . Плоскость, содержащей прямую пересечения плоскостей
. Плоскость, содержащей прямую пересечения плоскостей  B и параллельной вектору
B и параллельной вектору  , есть
, есть  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  это верно?
это верно?




 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 и
и  . Написать уравнение общего перпендикуляра к этим прямым.
. Написать уравнение общего перпендикуляра к этим прямым.










 равна
равна  . Тангенс половины угла при вершине
. Тангенс половины угла при вершине  ромба составляет 3/11. Составьте уравнения прямой
ромба составляет 3/11. Составьте уравнения прямой  .
.





 , уравнение касательной которой в точке
, уравнение касательной которой в точке  есть
есть  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 












 и пересекающей две прямые
и пересекающей две прямые  и
и 






















 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . Выбрать правильный ответ –
. Выбрать правильный ответ –  и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  пересекаются в точке
пересекаются в точке 
 и
и  не пересекаются
не пересекаются  , если
, если
 -(1x3)матрица
-(3x3)-матрица.
-(1x3)матрица
-(3x3)-матрица.





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 . Чему равна площадь треугольника, образованного точками
. Чему равна площадь треугольника, образованного точками  ,
,  и
и  –выберите правильный вариант
–выберите правильный вариант 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 






 ,
,  .
.




 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равно
. Чему равно  ?
? содержит две точки
содержит две точки  и параллельна оси
и параллельна оси  и оси
и оси  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  это верно?
это верно?




 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 






 .
.





 . Точки
. Точки  ,
,  и
и  лежат на прямой
лежат на прямой  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 параллельно прямым
параллельно прямым
 .
.




 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
? и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Определите – может ли быть вершиной образованного треугольника точка
образуют треугольник. Определите – может ли быть вершиной образованного треугольника точка





 и
и 





 . Найти уравнение высоты треугольника, образованного точками
. Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  ?
?





 и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильный вариант выбора точки
. Отметьте правильный вариант выбора точки 






 параллельно прямой
параллельно прямой  .
.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильные варианты выбора точки
. Отметьте правильные варианты выбора точки 






 ,
,  .
.




 . Отметьте точки, которые лежат на прямой
. Отметьте точки, которые лежат на прямой  :
:





 .
.





 . Точки
. Точки  ,
,  и
и  ) лежат на прямой
) лежат на прямой  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 параллельно прямым
параллельно прямым
 .
.




 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . При каких значениях
. При каких значениях  и
и  прямые
прямые  и
и  не пересекаются
не пересекаются




 и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Определите – может ли быть вершиной образованного треугольника точка
образуют треугольник. Определите – может ли быть вершиной образованного треугольника точка  при следующем значении
при следующем значении  и
и  -
-




 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 . Площадь треугольника, образованного точками
. Площадь треугольника, образованного точками  ,
,  и
и  , равна 2. Какое значение
, равна 2. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и
и 





 . Найти уравнение высоты треугольника, образованного точками
. Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  ?
?





 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Отметьте неправильные варианты выбора точки
. Отметьте неправильные варианты выбора точки 






 и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Отметьте правильные варианты выбора точки
. Отметьте правильные варианты выбора точки 






 параллельно прямой
параллельно прямой  .
.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  .
.




 . Отметьте точки, которые не лежат на прямой
. Отметьте точки, которые не лежат на прямой  :
:





 .
.





 . Точки
. Точки  ,
,  и
и  лежат на прямой
лежат на прямой  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 параллельно прямым
параллельно прямым
 .
.




 . точки
. точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Точка
образуют треугольник. Точка  – вершинa образованного треугольника. Какое значение
– вершинa образованного треугольника. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 ). Площадь треугольника, образованного точками
). Площадь треугольника, образованного точками  ,
,  и
и  , равна 3. Какое значение
, равна 3. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и
и 





 ). Найти уравнение высоты треугольника, образованного точками
). Найти уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  ?
?





 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  .
.




 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равен
. Чему равен  ?
? .
.





 , точки
, точки  и
и  . Отметьте точки, которые не лежат на прямой
. Отметьте точки, которые не лежат на прямой  и расположены внутри треугольника с вершинами в точках
и расположены внутри треугольника с вершинами в точках  – начала координат,
– начала координат,  и
и  :
:





 параллельно прямым
параллельно прямым
 .
.




 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . Точка
. Точка  лежит пересечении этих прямых
лежит пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Точка
образуют треугольник. Точка  – вершинa образованного треугольника. Какое значение
– вершинa образованного треугольника. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 . Площадь треугольника, образованного точками
. Площадь треугольника, образованного точками  ,
,  и
и  , равна 4. Какие значения
, равна 4. Какие значения  и
и  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 и
и 





 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 ,
,  .
.




 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равен
. Чему равен  ?
? .
.





 , точки
, точки  и
и  . Отметьте точки, которые лежат на прямой
. Отметьте точки, которые лежат на прямой  и расположены вне треугольника с вершинами в точках
и расположены вне треугольника с вершинами в точках  – начала координат,
– начала координат,  и
и  :
:





 параллельно прямым
параллельно прямым
 .
.




 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Точки
образуют треугольник. Точки  и
и  – две вершины образованного треугольника. Определите – третья вершина образованного треугольника является точкой пересечения следующих прямых
– две вершины образованного треугольника. Определите – третья вершина образованного треугольника является точкой пересечения следующих прямых и
и 
 и
и 
 и
и 
 и оси
и оси 
 и оси
и оси 
 и оси
и оси 
 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой
как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой  . Так же известно, что одна из этих вершин расположена на оси
. Так же известно, что одна из этих вершин расположена на оси  . Чему равна
. Чему равна  координата другой вершины?
координата другой вершины? и
и 




 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе угла между прямыми
лежит на биссектрисе угла между прямыми  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 и
и 




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  .
.




 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равно
. Чему равно  ?
? .
.





 , точки
, точки  и
и  . Отметьте точку, которая лежит на прямой
. Отметьте точку, которая лежит на прямой  и расположена между точками
и расположена между точками  и
и  :
:





 параллельно прямым
параллельно прямым
 .
.




 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 параллельно прямой
параллельно прямой  .
.




 и прямая
и прямая  . Точка
. Точка  лежит на пересечении этих прямых
лежит на пересечении этих прямых  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и прямую
и прямую  .
.




 ,
,  ,
,  . Пересекаясь друг с другом прямые
. Пересекаясь друг с другом прямые  ,
,  и
и  образуют треугольник. Точки
образуют треугольник. Точки  и
и  – две вершины образованного треугольника. Определите – будет ли третьей вершиной образованного треугольника являться следующая точка
– две вершины образованного треугольника. Определите – будет ли третьей вершиной образованного треугольника являться следующая точка





 перпендикулярно к плоскости
перпендикулярно к плоскости  .
.




 как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой
как вершина треугольника. Площадь треугольника равна 3. Две другие вершины расположены на прямой  , Также известно, что одна из этих вершин расположена на оси
, Также известно, что одна из этих вершин расположена на оси  . Чему равна
. Чему равна  координата другой вершины?
координата другой вершины? и
и 





 . Уравнение высоты треугольника, образованного точками
. Уравнение высоты треугольника, образованного точками  ,
,  и
и  , на сторону
, на сторону  есть уравнение
есть уравнение  . Какие значения
. Какие значения  и
и  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?




 и пересекающей две прямые
и пересекающей две прямые  и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе между прямыми
лежит на биссектрисе между прямыми  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 и
и 





 и
и  . Точка
. Точка  лежит на биссектрисе того угла между прямыми
лежит на биссектрисе того угла между прямыми  и
и  , внутри которого находится точка
, внутри которого находится точка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи? параллельно прямой
параллельно прямой  .
.




 ,
,  .
.





 . Точка
. Точка  лежит на прямой
лежит на прямой  . Чему равно
. Чему равно  ?
? ,
,  .
.





 , точки
, точки  и
и  . Отметьте точку, которая лежит на прямой
. Отметьте точку, которая лежит на прямой  и расположена вне отрезка
и расположена вне отрезка  :
:





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 ,
,  .
.





 ,
,  .
.





 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположенa между точками
и расположенa между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
,  .
.




 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 ,
,  .
.





 ,
,  .
.





 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположенa вне отрезка
и расположенa вне отрезка  . Какое значение
. Какое значение  из приведенных ниже, удовлетворяет условиям задачи?
из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 , точки
, точки  ,
,  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 ,
,  .
.





 ,
,  .
.





 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположенa между точками
и расположенa между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 , точки
, точки  ,
,  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каком из приведенных ниже значений
. При каком из приведенных ниже значений  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
, 






 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 ,
,  .
.





 ,
,  .
.





 , точки
, точки  и
и  . Точка
. Точка  лежит на прямой
лежит на прямой  и расположенa вне отрезка
и расположенa вне отрезка  . Какое значение
. Какое значение  из приведенных ниже, удовлетворяет условиям задачи?
из приведенных ниже, удовлетворяет условиям задачи?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 , точки
, точки  ,
,  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположена между точками
расположена между точками  и
и  ?
?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 ,
,  .
.





 ,
,  .
.





 . Точки
. Точки  ,
,  и
и  лежат на прямой
лежат на прямой  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположенa между точками
расположенa между точками  и
и  ?
?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 . Определить точку пресечения прямой
. Определить точку пресечения прямой  с осью
с осью  ?
?





 ,
,  , перпендикулярно плоскости
, перпендикулярно плоскости  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямым
параллельно прямым  ,
,  .
.





 параллельно прямой
параллельно прямой  .
.





 параллельно прямой
параллельно прямой  .
.





 и прямую
и прямую  ,
,  ,
, 






 перпендикулярно плоскости
перпендикулярно плоскости  .
.





 . Точки
. Точки  ,
,  и
и  лежат на прямой
лежат на прямой  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположенa между точками
расположенa между точками  и
и  ?
?





 . Определить точку пересечения прямой
. Определить точку пересечения прямой  с осью
с осью  ?
?





 . Точки
. Точки  ,
,  и
и  лежат на прямой
лежат на прямой  . При каком из приведенных ниже значении
. При каком из приведенных ниже значении  и
и  точка
точка  расположенa между точками
расположенa между точками  и
и  ?
?





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равен
. Чему равен  ?
? , точки
, точки  и
и  . Отметьте точки, которые не лежат на прямой
. Отметьте точки, которые не лежат на прямой  и расположены внутри треугольника с вершинами в точках
и расположены внутри треугольника с вершинами в точках  – начала координат,
– начала координат,  и
и  :
:





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равен
. Чему равен  ?
? , точки
, точки  и
и  . Отметьте точки, которые лежат на прямой
. Отметьте точки, которые лежат на прямой  и расположены вне треугольника с вершинами в точках
и расположены вне треугольника с вершинами в точках  – начала координат,
– начала координат,  и
и  :
:





 . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
? . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
? . Точка
. Точка  лежит на пересечении прямой
лежит на пересечении прямой  и оси
и оси  . Чему равно
. Чему равно  ?
?





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какое значения
. Какое значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  .Какое значение
.Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 , точки
, точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяют условиям задачи?
, из приведенных ниже, удовлетворяют условиям задачи?





 точки
точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какое значение
. Какое значение  , из приведенных ниже, не удовлетворяют условиям задачи?
, из приведенных ниже, не удовлетворяют условиям задачи?





 точки
точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена между точками
расположена между точками  и
и  . Какое значение
. Какое значение  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 точки
точки  и
и  . Точка пересечения прямой
. Точка пересечения прямой  с осью
с осью  расположена вне отрезка
расположена вне отрезка  . Какие значения
. Какие значения  , из приведенных ниже, удовлетворяет условиям задачи?
, из приведенных ниже, удовлетворяет условиям задачи?





 точки
точки  и
и  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  не расположенa между точками
не расположенa между точками  и
и  ?
?





 , точки
, точки  ,
,  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каком из приведенных ниже значений
. При каком из приведенных ниже значений  и
и  точка
точка  расположенa между точками
расположенa между точками  и
и  ?
?





 , точки
, точки  ,
,  . Точка
. Точка  - точка пересечения прямой
- точка пересечения прямой  с осью
с осью  . При каких из приведенных ниже значений
. При каких из приведенных ниже значений  и
и  точка
точка  расположенa между точками
расположенa между точками  и
и  ?
?




