Главная / Математика / Математическая экономика

Математическая экономика - ответы на тесты Интуит

Правильные ответы выделены зелёным цветом.
Все ответы: Математическая экономика – это набор моделей в той или иной степени правильно описывающих процессы в экономике.
Смотрите также:
Экономика
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''-y=0 \\ y(0)=0 \\ y'(0)=1
1,18
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,94
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 0 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,46
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math2
math5
math4
math3
math120
240
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 1 рубль.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,225
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти равновесную цену. Ответ введите с точностью до 3-го знака после запятой.
0,429
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 3,1? Ответ введите с точностью до 1-го знака после запятой.
1,0
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти выпуск продукции в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
1,44
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится денежная масса, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
1,125
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math0
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,492
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти коэффициенты уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
k=111,4; b=-224,4
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,15
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
Найти максимально достижимое значение объёма производства.
50
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1. Ответ введите с точностью до 1-го знака после запятой.
110,5
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0224
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
-0,0775
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,77
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,15
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math при math. Ответ введите с точностью до 2-го знака после запятой.
4,45
В экономике два сектора. Известна матрица межотраслевых связей:
0,20,25
0,30,15
Производство по отраслям составляет:
8
5
Найти конечное потребление.
(1)
5,15
1,85
(2)
3,3
2,6
(3)
1,8
5,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 3-го знака после запятой.
0,501
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
6,91
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз math. Ответ введите с точностью до 2-го знака после запятой.
12,35
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,74
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''+y=0 \\ y(0)=0 \\ y'(0)=1
0,84
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,81
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 1 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,68
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math2
math5
math4
math4
math3
math9
math120
270
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении затрат на рабочую силу на 1 рубль.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,667
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти постоянную времени процесса установления цены. Ответ введите с точностью до 3-го знака после запятой.
0,143
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 3,5? Ответ введите с точностью до 1-го знака после запятой.
5,2
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти суммарную прибыль в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
4,26
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится капитал, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
1,306
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math0
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,492
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти дисперсию уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
7598,5
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,32
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
Найти постоянную времени процесса (обратную величину коэффициента стоящего перед t). Ответ введите с точностью до 1-го знака после запятой.
2,5
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Ответ введите с точностью до 3-го знака после запятой.
151,663
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение большего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,2348
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение модуля (r) корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,2236
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
4
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,74
Задано дифференциальное уравнение math. Найти его решение при условии math. Чему равно y(2). Ответ введите с точностью до 2-го знака после запятой.
0,86
В экономике два сектора. Известна матрица межотраслевых связей:
0,20,25
0,30,15
Конечное потребление по отраслям составляет:
2
3
Производство по отраслям.
(1)
4,049587
4,958678
(2)
5,6
3,466667
(3)
2,848485
3,757576
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 2. Ответ введите с точностью до 3-го знака после запятой.
0,245
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
34,55
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз производство на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
2,13
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти производство на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
2,36
Решить систему линейных алгебраических уравнений. В ответе указать значение y. \begin{cases} 2x+3y+5z=15 \\ x+2y+3z=9 \\ 4x+6y+z=12 \end{cases}
1
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,96
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 2 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,49
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math2
math5
math4
math3
math120
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,446
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) в момент времени math. Ответ введите с точностью до 3-го знака после запятой.
2,333
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 4? Ответ введите с точностью до 1-го знака после запятой.
10,2
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти выпуск продукции в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
1,63
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится объём производства, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
1,143
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math0
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,670
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти среднее квадратичное отклонение уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
87,2
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,52
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
На сколько процентов уменьшится цена к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
22,8
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Ответ введите с точностью до 3-го знака после запятой.
186,316
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение меньшего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0852
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,7826
В экономике три сектора. Известна матрица межотраслевых связей:
0,10,30,15
0,20,10,1
0,050,20,2
Производство по отраслям составляет:
5
7
9
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,77
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
2
В экономике три сектора. Известна матрица межотраслевых связей:
0,10,30,15
0,20,10,1
0,050,20,2
Производство по отраслям составляет:
5
7
9
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать долю в портфеле бумаги номер 3. Ответ введите с точностью до 3-го знака после запятой.
0,254
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельные инвестиции. Ответ введите с точностью до 2-го знака после запятой.
2,42
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз удельные инвестиции при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
3,13
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти инвестиции на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,60
Дана таблица значений признака math и их частот math. Найти среднее значение.
math3579
math2522494
Ответ введите с точностью до 2-го знака после запятой.
5,64
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,88
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 0 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,54
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math2
math5
math4
math3
math120
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения прибыли).
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
2,966
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) через 0,1 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
2,206
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 5? Ответ введите с точностью до 1-го знака после запятой.
19,4
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти суммарную прибыль в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
3,28
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменятся цены, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
0,984
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math0
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,330
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти коэффициенты уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
a=10,4; b=-3,7; c=5,7
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,23
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
На сколько процентов увеличится объём производства к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
15,2
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,094
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
634,4
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,6225
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
0,293
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,62
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
3
В экономике три сектора. Известна матрица межотраслевых связей:
0,10,30,15
0,20,10,1
0,050,20,2
Конечное потребление по отраслям составляет:
2
1
3
Найти производство по отраслям.
(1)
3,813298
2,470277
4,6059
(2)
11,13295
6,568387
6,170355
(3)
6,975184
9,242119
6,170355
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
0,232
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельное потребление. Ответ введите с точностью до 2-го знака после запятой.
4,49
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз потребление на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
2,13
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти потребление на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,65
Дана таблица значений признака math и их частот math. Найти дисперсию.
math3579
math2522494
Ответ введите с точностью до 4-го знака после запятой.
3,1904
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,99
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 1 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,32
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math2
math5
math4
math4
math3
math9
math120
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 1 рубль.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,122
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) через 0,5 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
1,809
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 2,9? Ответ введите с точностью до 1-го знака после запятой.
1,1
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти выпуск продукции в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
1,73
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится денежная масса, если процентная ставка уменьшится до 5.
1
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,498
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти дисперсию уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
493,5
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
1,00
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
На сколько процентов сократится выручка к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
11,1
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,397
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
-541,5
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
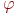Найти значение math (в радианах), входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,6719
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,45
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
0,86
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
12,11
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,10,20,050,2
0,20,20,050,2
0,150,10,10,15
0,30,250,20,15
Производство по отраслям составляет:
6
7
9
8
Найти конечное потребление.
(1)
4,05
4,65
3,7
6,55
(2)
4,25
5,05
3,65
6,7
(3)
2,45
2,85
1,7
4,15
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать указать среднее квадратичное отклонение доходности портфеля портфеля. Ответ введите с точностью до 3-го знака после запятой.
0,482
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,45
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,50
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится math. Ответ введите с точностью до 2-го знака после запятой.
1,50
Заданы пары значений величин x и y.
math12345
math1225314254
Найти их ковариацию. Ответ введите с точностью до 1-го знака после запятой.
20,2
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,92
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
На сколько процентов увеличится производства сектора 2 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,51
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math2
math5
math4
math4
math3
math9
math120
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении затрат на рабочую силу на 1 рубль.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,167
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) через 1,5 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
1,298
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 2,5? Ответ введите с точностью до 1-го знака после запятой.
5,3
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти суммарную прибыль в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
2,51
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится капитал, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
0,969
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math-0,05
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,498
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти среднее квадратичное отклонение уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
22,2
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math уменьшатся на 30%? Ответ введите с точностью до 2-го знака после запятой.
0,81
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
На сколько процентов сократится прибыль к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
14,8
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=10. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,956
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
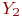Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
38,2
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
92,9
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,13
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math на 40%? Ответ введите с точностью до 2-го знака после запятой.
0,62
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
3,99
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,10,20,050,2
0,20,20,050,2
0,150,10,10,15
0,30,250,20,15
Конечное потребление по отраслям составляет:
2
5
3
2
Найти конечное потребление.
(1)
7,283676
11,01204
7,422326
9,908916
(2)
9,386524
11,54058
10,58033
13,23537
(3)
3,09774
6,407514
5,562772
6,544837
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 3-го знака после запятой.
3,554
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,90
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,13
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится производство на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
1,13
Заданы пары значений величин x и y.
math12345
math1225314254
Найти их коэффициент корреляции. Ответ введите с точностью до 3-го знака после запятой.
0,995
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,99
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти суммарный продукт. Ответ введите с точностью до 2-го знака после запятой.
15,88
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены третьего товара в два раза?
math2
math5
math4
math4
math3
math9
math120
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,145
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) через 2 постоянные времени. Ответ введите с точностью до 3-го знака после запятой.
1,180
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 2? Ответ введите с точностью до 1-го знака после запятой.
10,8
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти выпуск продукции в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
1,08
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится объём производства, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
0,984
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,620
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти во сколько раз дисперсия уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
15,4
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,07
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
На сколько процентов сократится прибыль за вычетом инвестиций к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
18,0
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,004
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
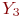Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
15,0
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
622,2
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,26
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
0,93
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
36,05
В экономике пять секторов. Известна матрица межотраслевых связей:
0,30,10,350,150,25
0,20,20,20,350,15
0,10,20,20,10,05
0,20,30,150,20,15
0,10,150,10,150,05
Производство по отраслям составляет:
5
6
2
8
6
Найти конечное потребление.
(1)
5,5
6,3
3,2
5,6
3,1
(2)
4
4,6
2,45
3,75
1,95
(3)
5,25
5,85
3,15
4,95
2,65
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 5%. В ответе указать указать максимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 3-го знака после запятой.
6,446
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменятся удельные инвестиции, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,90
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличатся удельные инвестиции при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,26
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,26
Заданы пары значений величин x и y.
math12345
math1225314254
Построить уравнение регрессии math и найти остаточную дисперсию. Ответ введите с точностью до 2-го знака после запятой.
3,57
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,95
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,46
math0,68
math0,49
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти параметр math в суммарной производственной функции (X_0+X_1+X_2)=A(K_0+K_1+K_2)^{\alpha}(L_0+L_1+L_2)^{1-\alpha} \\ \alpha=\frac{\alpha_0+\alpha_1+\alpha_2}{3} . Ответ введите с точностью до 2-го знака после запятой.
17,26
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены всех товаров в два раза?
math2
math5
math4
math4
math3
math9
math120
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения производства).
math1
math10
math2
math5
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
1,361
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math5
math2
math5
math2
math1
math1
Найти цену (в долях от равновесной цены) через 3 постоянные времени. Ответ введите с точностью до 3-го знака после запятой.
1,066
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,05
math3
На сколько процентов уменьшится количество занятых, если math составит 1? Ответ введите с точностью до 1-го знака после запятой.
22,2
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a15
b6
c2
d1
Найти суммарную прибыль в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
5,04
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменятся цены, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
1,016
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,5
math-0,05
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,380
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math746811732353774706657801030
Найти во сколько раз среднее квадратичное отклонение уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
3,9
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,15
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math100
math2
math0,5
math0,4
math30
math5
Во сколько раз увеличится прибыль за вычетом инвестиций к моменту времени t=1 если норму инвестирования уменьшить в два раза? Ответ введите с точностью до 1-го знака после запятой.
1,6
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,024
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,02
math0,3
math5
Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
9,0
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,05
math0,3
math5
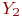Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
38,5
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math) Ответ введите с точностью до 2-го знака после запятой.
0,95
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
0,76
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
4
В экономике пять секторов. Известна матрица межотраслевых связей:
0,30,10,350,150,25
0,20,20,20,350,15
0,10,20,20,10,05
0,20,30,150,20,15
0,10,150,10,150,05
Конечное потребление по отраслям составляет:
5
6
2
8
6
Найти производство по отраслям.
(1)
64,97967
70,19194
39,00289
67,18347
38,95218
(2)
19,18457
21,33295
10,11776
21,18692
11,90789
(3)
33,2569
32,21004
15,83868
29,84722
17,24765
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится удельное потребление, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,67
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится удельное потребление при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,65
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) изменится потребление на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
0,65
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''-y=0 \\ y(0)=1 \\ y'(0)=0
1,72
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,88
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 0 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,36
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math3
math6
math2
math1
math120
80
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 1 рубль.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,531
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти равновесную цену. Ответ введите с точностью до 3-го знака после запятой.
0,600
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 3,1? Ответ введите с точностью до 1-го знака после запятой.
2,5
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти выпуск продукции в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
1,92
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится денежная масса, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
1,150
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math0
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,517
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти коэффициенты уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
k=110,9; b=-223,5
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,23
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
Найти максимально достижимое значение объёма производства.
20
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1. Ответ введите с точностью до 1-го знака после запятой.
187,5
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0041
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
-0,1024
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,66
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,23
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math при math. Ответ введите с точностью до 2-го знака после запятой.
1,47
В экономике два сектора. Известна матрица межотраслевых связей:
0,10,3
0,20,1
Производство по отраслям составляет:
5
4
Найти конечное потребление.
(1)
5,15
1,85
(2)
3,3
2,6
(3)
1,8
5,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 3-го знака после запятой.
-0,741
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
3,09
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз math. Ответ введите с точностью до 2-го знака после запятой.
7,04
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти math, если math. Ответ введите с точностью до 2-го знака после запятой.
0,79
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''+y=0 \\ y(0)=1 \\ y'(0)=0
0,54
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,66
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 1 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,52
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math3
math6
math3
math2
math1
math4
math150
200
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении затрат на рабочую силу на 1 рубль.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,179
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти постоянную времени процесса установления цены. Ответ введите с точностью до 3-го знака после запятой.
0,200
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 3,5? Ответ введите с точностью до 1-го знака после запятой.
12,1
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти суммарную прибыль в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
5,35
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится капитал, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
2,041
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math0
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,517
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти дисперсию уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
8852,8
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,41
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
Найти постоянную времени процесса (обратную величину коэффициента стоящего перед t). Ответ введите с точностью до 2-го знака после запятой.
1,25
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Ответ введите с точностью до 3-го знака после запятой.
338,778
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение большего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,1370
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение модуля (r) корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,2000
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
8
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,62
Задано дифференциальное уравнение math. Найти его решение при условии math. Ответ введите с точностью до 2-го знака после запятой.
1,00
В экономике два сектора. Известна матрица межотраслевых связей:
0,10,3
0,20,1
Конечное потребление по отраслям составляет:
4
2
Производство по отраслям.
(1)
4,049587
4,958678
(2)
5,6
3,466667
(3)
2,848485
3,757576
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 2. Ответ введите с точностью до 3-го знака после запятой.
1,254
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
8,83
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз производство на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
1,34
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти производство на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,93
Решить систему линейных алгебраических уравнений. В ответе указать значение y. \begin{cases} 2x+3y+5z=39 \\ x+2y+3z=23 \\ 4x+6y+z=33 \end{cases}
2
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,93
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 2 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,63
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math3
math6
math2
math1
math120
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,355
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) в момент времени math. Ответ введите с точностью до 3-го знака после запятой.
1,667
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 4? Ответ введите с точностью до 1-го знака после запятой.
23,4
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти выпуск продукции в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
2,16
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится объём производства, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
1,429
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math0
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,659
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти среднее квадратичное отклонение уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
94,1
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,74
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
На сколько процентов уменьшится цена к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
38,0
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Ответ введите с точностью до 3-го знака после запятой.
337,653
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение меньшего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0730
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,6000
В экономике три сектора. Известна матрица межотраслевых связей:
0,150,250,25
0,250,050,2
0,10,150,3
Производство по отраслям составляет:
8
6
4
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,66
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
4
В экономике три сектора. Известна матрица межотраслевых связей:
0,150,250,25
0,250,050,2
0,10,150,3
Производство по отраслям составляет:
8
6
4
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать долю в портфеле бумаги номер 3. Ответ округлите и введите с точностью до 2-го знака после запятой.
0,49
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельные инвестиции. Ответ введите с точностью до 2-го знака после запятой.
0,62
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз удельные инвестиции при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
1,34
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти инвестиции на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
0,29
Дана таблица значений признака math и их частот math. Найти среднее значение.
math2468
math12354013
Ответ введите с точностью до 2-го знака после запятой.
5,08
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,77
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 0 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,64
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math3
math6
math2
math1
math120
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения прибыли).
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,336
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) через 0,1 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
1,603
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 5? Ответ введите с точностью до 1-го знака после запятой.
43,8
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти суммарную прибыль в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
4,20
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменятся цены, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
0,805
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math0
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,341
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти коэффициенты уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
a=10,6; b=-5,0; c=8,5
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,27
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
На сколько процентов увеличится объём производства к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
38,0
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
8,527
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
1549,6
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,8000
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
1,743
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,46
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
4
В экономике три сектора. Известна матрица межотраслевых связей:
0,10,30,15
0,20,10,1
0,050,20,2
Конечное потребление по отраслям составляет:
6
2
3
Найти производство по отраслям.
(1)
3,813298
2,470277
4,6059
(2)
11,13295
6,568387
6,170355
(3)
6,975184
9,242119
6,170355
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
1,519
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельное потребление. Ответ введите с точностью до 2-го знака после запятой.
2,47
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз потребление на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
1,34
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти потребление на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,64
Дана таблица значений признака math и их частот math. Найти дисперсию.
math2467
math12354013
Ответ введите с точностью до 4-го знака после запятой.
2,9936
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,98
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 1 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,48
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math3
math6
math3
math2
math1
math4
math150
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 1 рубль.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,336
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) через 0,5 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
1,404
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 2,9? Ответ введите с точностью до 1-го знака после запятой.
2,5
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти выпуск продукции в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
2,30
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится денежная масса, если процентная ставка уменьшится до 4.
1
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,498
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти дисперсию уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
1662,9
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
1,03
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
На сколько процентов сократится выручка к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
14,4
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,535
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
-1453,4
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
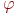Найти значение math (в радианах), входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,9273
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,19
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
0,96
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
-3,83
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,050,10,20,2
0,050,20,20,2
0,10,150,150,1
0,20,30,150,25
Производство по отраслям составляет:
5
8
7
9
Найти конечное потребление.
(1)
4,05
4,65
3,7
6,55
(2)
4,25
5,05
3,65
6,7
(3)
2,45
2,85
1,7
4,15
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать указать среднее квадратичное отклонение доходности портфеля портфеля. Ответ введите с точностью до 3-го знака после запятой.
1,233
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,19
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,45
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится math. Ответ введите с точностью до 2-го знака после запятой.
1,45
Заданы пары значений величин x и y.
math12345
math718314562
Найти их ковариацию. Ответ введите с точностью до 1-го знака после запятой.
27,4
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,84
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
На сколько процентов увеличится производства сектора 2 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,37
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math3
math6
math3
math2
math1
math4
math150
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении затрат на рабочую силу на 1 рубль.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,236
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) через 1,5 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
1,149
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 2,5? Ответ введите с точностью до 1-го знака после запятой.
12,9
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти суммарную прибыль в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
3,29
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится капитал, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
0,648
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math-0,05
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,498
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти среднее квадратичное отклонение уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
40,8
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math уменьшатся на 30%? Ответ введите с точностью до 2-го знака после запятой.
0,75
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
На сколько процентов сократится прибыль к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
21,9
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=10. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,002
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
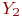Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
25,1
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
96,3
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,06
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math на 40%? Ответ введите с точностью до 2-го знака после запятой.
0,63
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
0,29
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,050,10,20,2
0,050,20,20,2
0,10,150,150,1
0,20,30,150,25
Конечное потребление по отраслям составляет:
3
4
5
3
Найти конечное потребление.
(1)
7,283676
11,01204
7,422326
9,908916
(2)
9,386524
11,54058
10,58033
13,23537
(3)
3,09774
6,407514
5,562772
6,544837
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 3-го знака после запятой.
6,302
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,38
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,06
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится производство на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
1,06
Заданы пары значений величин x и y.
math12345
math718314562
Найти их коэффициент корреляции. Ответ введите с точностью до 3-го знака после запятой.
0,997
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,99
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти суммарный продукт. Ответ введите с точностью до 2-го знака после запятой.
17,12
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены третьего товара в два раза?
math3
math6
math3
math2
math1
math4
math150
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,371
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) через 2 постоянные времени. Ответ введите с точностью до 3-го знака после запятой.
1,090
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 2? Ответ введите с точностью до 1-го знака после запятой.
26,6
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти выпуск продукции в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
1,44
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится объём производства, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
0,805
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,684
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти во сколько раз дисперсия уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
5,3
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,11
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
На сколько процентов сократится прибыль за вычетом инвестиций к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
28,2
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,301
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
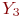Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
7,2
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math3
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
591,9
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,12
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
0,90
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
-15,67
В экономике пять секторов. Известна матрица межотраслевых связей:
0,250,050,30,10,35
0,150,150,150,30,2
0,050,150,150,050,2
0,150,250,10,150,15
0,050,10,050,10,1
Производство по отраслям составляет:
4
5
1
7
5
Найти конечное потребление.
(1)
5,5
6,3
3,2
5,6
3,1
(2)
4
4,6
2,45
3,75
1,95
(3)
5,25
5,85
3,15
4,95
2,65
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 10%. В ответе указать указать максимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 3-го знака после запятой.
13,698
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменятся удельные инвестиции, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,38
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличатся удельные инвестиции при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,12
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,12
Заданы пары значений величин x и y.
math12345
math718314562
Построить уравнение регрессии math и найти остаточную дисперсию. Ответ введите с точностью до 2-го знака после запятой.
4,10
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,90
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,36
math0,52
math0,63
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти параметр math в суммарной производственной функции (X_0+X_1+X_2)=A(K_0+K_1+K_2)^{\alpha}(L_0+L_1+L_2)^{1-\alpha} \\ \alpha=\frac{\alpha_0+\alpha_1+\alpha_2}{3} . Ответ введите с точностью до 2-го знака после запятой.
18,74
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены всех товаров в два раза?
math3
math6
math3
math2
math1
math4
math150
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения производства).
math1
math5
math1
math2
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,770
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math6
math3
math2
math3
math1
math1
Найти цену (в долях от равновесной цены) через 3 постоянные времени. Ответ введите с точностью до 3-го знака после запятой.
1,033
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,1
math3
На сколько процентов уменьшится количество занятых, если math составит 1? Ответ введите с точностью до 1-го знака после запятой.
56,3
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a12
b4
c0,5
d1
Найти суммарную прибыль в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
6,27
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменятся цены, если процентная ставка уменьшится до 4. Ответ введите с точностью до 3-го знака после запятой.
1,242
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,6
math0
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,316
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math551741902203984526857601050
Найти во сколько раз среднее квадратичное отклонение уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
2,3
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,19
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math80
math4
math0,5
math0,4
math10
math5
Во сколько раз увеличится прибыль за вычетом инвестиций к моменту времени t=1 если норму инвестирования уменьшить в два раза? Ответ введите с точностью до 1-го знака после запятой.
1,8
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math4
math250
math0,06
math25
math0,07
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,037
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,01
math0,2
math3
Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
4,3
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,04
math0,2
math5
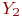Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
25,4
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math) Ответ введите с точностью до 2-го знака после запятой.
0,90
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
0,78
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
8
В экономике пять секторов. Известна матрица межотраслевых связей:
0,250,050,30,10,35
0,150,150,150,30,2
0,050,150,150,050,2
0,150,250,10,150,15
0,050,10,050,10,1
Конечное потребление по отраслям составляет:
4
5
1
7
5
Найти производство по отраслям.
(1)
64,97967
70,19194
39,00289
67,18347
38,95218
(2)
19,18457
21,33295
10,11776
21,18692
11,90789
(3)
33,2569
32,21004
15,83868
29,84722
17,24765
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится удельное потребление, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,89
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится удельное потребление при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,87
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) изменится потребление на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
0,87
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''-y=0 \\ y(0)=0 \\ y'(0)=1
1,18
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,83
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 0 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,58
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math4
math8
math5
math8
math120
150
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 1 рубль.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,148
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти равновесную цену. Ответ введите с точностью до 3-го знака после запятой.
1,667
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 3,1? Ответ введите с точностью до 1-го знака после запятой.
0,4
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти выпуск продукции в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
0,89
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится денежная масса, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
1,175
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math0
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,517
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти коэффициенты уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
k=109,7; b=-217,0
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,32
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
Найти максимально достижимое значение объёма производства.
15
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1.
290
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0102
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение дискриминанта характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
-0,0416
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,55
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,32
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math при math. Ответ введите с точностью до 2-го знака после запятой.
5,92
В экономике два сектора. Известна матрица межотраслевых связей:
0,10,15
0,20,05
Производство по отраслям составляет:
3
6
Найти конечное потребление.
(1)
5,15
1,85
(2)
3,3
2,6
(3)
1,8
5,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 3-го знака после запятой.
-1,983
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
2,08
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз math. Ответ введите с точностью до 2-го знака после запятой.
22,43
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти math, если math. Ответ введите с точностью до 2-го знака после запятой.
2,59
Решите задачу Коши для дифференциального уравнения. Укажите значение функции при х=1. Ответ введите с точностью до 2-го знака после запятой. y''+y=0 \\ y(0)=1 \\ y'(0)=1
1,38
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,54
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 1 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,32
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Какова максимальная суммарная полезность.
math4
math8
math2
math5
math8
math7
math200
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении затрат на рабочую силу на 1 рубль.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,581
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти постоянную времени процесса установления цены. Ответ введите с точностью до 3-го знака после запятой.
0,167
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 3,5? Ответ введите с точностью до 1-го знака после запятой.
1,9
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти суммарную прибыль в случае равновесия Курно. Ответ введите с точностью до 2-го знака после запятой.
3,34
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится капитал, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
3,628
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math0
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,517
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти дисперсию уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
6438,3
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,52
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
Найти постоянную времени процесса (обратную величину коэффициента стоящего перед t). Ответ введите с точностью до 3-го знака после запятой.
0,625
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Ответ введите с точностью до 3-го знака после запятой.
864,826
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение большего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,1831
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение модуля (r) корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,1732
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
2
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,52
Задано дифференциальное уравнение math. Найти его решение при условии math. Ответ введите с точностью до 2-го знака после запятой.
(-2,30)
В экономике два сектора. Известна матрица межотраслевых связей:
0,10,15
0,20,05
Конечное потребление по отраслям составляет:
2
3
Производство по отраслям.
(1)
4,049587
4,958678
(2)
5,6
3,466667
(3)
2,848485
3,757576
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 2. Ответ введите с точностью до 3-го знака после запятой.
2,262
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти math. Ответ введите с точностью до 2-го знака после запятой.
1,49
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз производство на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
3,47
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти производство на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
2,92
Решить систему линейных алгебраических уравнений. В ответе указать значение y. \begin{cases} 2x+3y+5z=22 \\ x+2y+3z=13 \\ 4x+6y+z=35 \end{cases}
3
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,89
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 2 при увеличении его капитала на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,51
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math4
math8
math5
math8
math120
Ответ введите с точностью до 2-го знака после запятой.
1,25
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько рублей увеличится прибыль при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,365
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) в момент времени math. Ответ введите с точностью до 3-го знака после запятой.
0,600
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 4? Ответ введите с точностью до 1-го знака после запятой.
3,8
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти выпуск продукции в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
1,00
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменится объём производства, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
1,905
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math0
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,659
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти среднее квадратичное отклонение уравнения линейной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
80,2
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
2,00
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
На сколько процентов уменьшится цена к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
72,5
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Ответ введите с точностью до 3-го знака после запятой.
535,235
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение меньшего корня характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,0819
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,8083
В экономике три сектора. Известна матрица межотраслевых связей:
0,150,150,25
0,10,250,2
0,20,10,3
Производство по отраслям составляет:
6
8
3
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math увеличится в 3 раза? Ответ введите с точностью до 2-го знака после запятой.
2,55
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
3
В экономике три сектора. Известна матрица межотраслевых связей:
0,150,150,25
0,10,250,2
0,20,10,3
Производство по отраслям составляет:
6
8
3
Найти конечное потребление.
(1)
1,05
4,4
5,55
(2)
4,3
2,9
1,1
(3)
3,15
4,8
0,1
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать долю в портфеле бумаги номер 3. Ответ введите с точностью до 3-го знака после запятой.
0,721
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельные инвестиции. Ответ введите с точностью до 2-го знака после запятой.
0,10
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз удельные инвестиции при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
3,47
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти инвестиции на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,17
Дана таблица значений признака math и их частот math. Найти среднее значение.
math161116
math21303217
Ответ введите с точностью до 2-го знака после запятой.
8,25
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,68
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 0 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,42
Пусть потребитель может использовать два товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math4
math8
math5
math8
math120
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения прибыли).
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
3,921
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) через 0,1 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
0,638
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 5? Ответ введите с точностью до 1-го знака после запятой.
7,5
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти суммарную прибыль в случае равновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
2,60
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз по сравнению с периодом стабильности изменятся цены, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
0,617
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math0
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,341
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти коэффициенты уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
a=9,8; b=1,5; c=-0,5
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,31
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
На сколько процентов увеличится объём производства к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
36,2
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math6
math150
math0,04
math15
math0,03
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
48,138
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
922,1
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение math, входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,5888
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
5,679
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
1,31
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти, при каком значении math решение становится неустойчивым.
6
В экономике три сектора. Известна матрица межотраслевых связей:
0,10,30,15
0,20,10,1
0,050,20,2
Конечное потребление по отраслям составляет:
3
5
2
Найти производство по отраслям.
(1)
3,813298
2,470277
4,6059
(2)
11,13295
6,568387
6,170355
(3)
6,975184
9,242119
6,170355
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать дисперсию портфеля. Ответ введите с точностью до 3-го знака после запятой.
5,191
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти удельное потребление. Ответ введите с точностью до 2-го знака после запятой.
1,98
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз потребление на одного занятого при math больше, чем при math. Ответ введите с точностью до 2-го знака после запятой.
3,47
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти потребление на одного работающего при math, если math. Ответ введите с точностью до 2-го знака после запятой.
1,75
Дана таблица значений признака math и их частот math. Найти дисперсию.
math161116
math12354013
Ответ введите с точностью до 4-го знака после запятой.
25,1675
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,97
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 1 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,68
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены первого товара в два раза?
math4
math8
math2
math5
math8
math7
math200
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 1 рубль.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,077
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) через 0,5 от постоянной времени. Ответ введите с точностью до 3-го знака после запятой.
0,757
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 2,9? Ответ введите с точностью до 1-го знака после запятой.
2,9
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти выпуск продукции в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
1,07
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится денежная масса, если процентная ставка уменьшится до 3.
1
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста производства. Ответ введите с точностью до 3-го знака после запятой.
1,552
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти дисперсию уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
53,3
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
1,07
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
На сколько процентов сократится выручка к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
62,5
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
11,858
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
-831,4
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
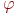Найти значение math (в радианах), входящего в выражение для корней характеристического уравнения. Ответ введите с точностью до 4-го знака после запятой.
0,6296
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,17
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза, а math уменьшится на 30%? Ответ введите с точностью до 2-го знака после запятой.
1,07
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
-2,84
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,050,1500,15
0,150,1500,15
0,10,050,050,1
0,250,20,150,1
Производство по отраслям составляет:
4
9
5
6
Найти конечное потребление.
(1)
4,05
4,65
3,7
6,55
(2)
4,25
5,05
3,65
6,7
(3)
2,45
2,85
1,7
4,15
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,17
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,54
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится math. Ответ введите с точностью до 2-го знака после запятой.
1,54
Заданы пары значений величин x и y.
math12345
math2334435558
Найти их ковариацию. Ответ введите с точностью до 1-го знака после запятой.
18,2
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,76
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
На сколько процентов увеличится производства сектора 2 при увеличении числа занятых в нём на 1%? Ответ введите с точностью до 2-го знака после запятой.
0,49
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены второго товара в два раза?
math4
math8
math2
math5
math8
math7
math200
1
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении затрат на рабочую силу на 1 рубль.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,105
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) через 1,5 от постоянной времени. Ответ введите с точностью до 4-го знака после запятой.
0,9118
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 2,5? Ответ введите с точностью до 1-го знака после запятой.
1,9
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти суммарную прибыль в случае неравновесия Стакельберга. Ответ введите с точностью до 2-го знака после запятой.
2,01
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится капитал, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
0,381
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math-0,05
math0,6
math0,4
В ответе укажите коэффициент прироста производства. Ответ введите с точностью до 3-го знака после запятой.
0,552
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти среднее квадратичное отклонение уравнения квадратичной регрессии math. Ответ введите с точностью до 1-го знака после запятой.
7,3
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math и math уменьшатся на 30%? Ответ введите с точностью до 2-го знака после запятой.
0,7
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
На сколько процентов сократится прибыль к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
76,6
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 1 значение объёма производства (y) для t=10. Затем найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=10. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
42,422
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
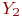Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
34,7
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
90,7
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,19
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math уменьшится на 30%, а math на 40%? Ответ введите с точностью до 2-го знака после запятой.
0,64
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
1,15
В экономике четыре сектора. Известна матрица межотраслевых связей:
0,050,1500,15
0,150,1500,15
0,10,050,050,1
0,250,20,150,1
Конечное потребление по отраслям составляет:
1
4
4
3
Найти конечное потребление.
(1)
7,283676
11,01204
7,422326
9,908916
(2)
9,386524
11,54058
10,58033
13,23537
(3)
3,09774
6,407514
5,562772
6,544837
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать указать минимальную доходность портфеля (по правилу 3-х сигм). Ответ введите с точностью до 3-го знака после запятой.
8,165
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится math, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
4,67
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится производство на одного занятого при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
1,19
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличится производство на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
1,19
Заданы пары значений величин x и y.
math12345
math2334435558
Найти их коэффициент корреляции. Ответ введите с точностью до 3-го знака после запятой.
0,987
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов производства при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,98
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти суммарный продукт. Ответ введите с точностью до 2-го знака после запятой.
15,70
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены третьего товара в два раза?
math4
math8
math2
math5
math8
math7
math200
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти на сколько единиц увеличится производство (math) при увеличении капитала на 0,5 рубля и затрат на рабочую силу на 0,5 рубля.
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
0,091
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) через 2 постоянные времени. Ответ введите с точностью до 4-го знака после запятой.
0,9468
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 2? Ответ введите с точностью до 1-го знака после запятой.
3,9
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти выпуск продукции в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
0,67
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменится объём производства, если процентная ставка уменьшится до 5. Ответ введите с точностью до 3-го знака после запятой.
0,617
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math-0,05
math0,6
math0,4
В ответе укажите коэффициент роста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
0,531
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти во сколько раз дисперсия уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
120,8
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,15
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
На сколько процентов сократится прибыль за вычетом инвестиций к моменту времени t=1. Ответ введите с точностью до 1-го знака после запятой.
88,5
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=1. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=1. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
2,049
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
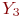Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
14,5
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
Найти значение коэффициента math. Ответ введите с точностью до 1-го знака после запятой.
862,6
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,38
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
0,87
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти значение math. Ответ введите с точностью до 2-го знака после запятой.
-14,94
В экономике пять секторов. Известна матрица межотраслевых связей:
0,250,350,250,10,1
0,150,20,150,30,2
0,050,20,050,050,2
0,150,150,150,150,3
0,050,10,050,10,15
Производство по отраслям составляет:
5
6
2
8
6
Найти конечное потребление.
(1)
5,5
6,3
3,2
5,6
3,1
(2)
4
4,6
2,45
3,75
1,95
(3)
5,25
5,85
3,15
4,95
2,65
Имеются данные о доходности трёх ценных бумаг за пять периодов.
R1R2R3
259
377
2610
485
378
Составить портфель ценных бумаг, обеспечивающий доходность 15%. В ответе указать указать долю в портфеле бумаги номер 1. Ответ введите с точностью до 3-го знака после запятой.
21,835
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменятся удельные инвестиции, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
4,67
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличатся удельные инвестиции при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
2,38
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) увеличатся инвестиции на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
2,38
Заданы пары значений величин x и y.
math12345
math2334435558
Построить уравнение регрессии math и найти остаточную дисперсию. Ответ введите с точностью до 2-го знака после запятой.
7,03
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math). Ответ введите с точностью до 2-го знака после запятой.
0,85
Пусть производственные функции секторов экономики имеют вид: X_0=6,19 K_0^{\alpha_0}L_0^{1-\alpha_0} \\ X_1=1,35 K_1^{\alpha_1}L_1^{1-\alpha_1} \\ X_2=2,71 K_2^{\alpha_2}L_2^{1-\alpha_2}
math0,58
math0,32
math0,51
Капиталы секторов и количество занятых в них составляет:
math1
math2
math2
math2
math3
math1
Найти параметр math в суммарной производственной функции (X_0+X_1+X_2)=A(K_0+K_1+K_2)^{\alpha}(L_0+L_1+L_2)^{1-\alpha} \\ \alpha=\frac{\alpha_0+\alpha_1+\alpha_2}{3} . Ответ введите с точностью до 2-го знака после запятой.
17,29
Пусть потребитель может использовать три товара в количествах math и math. Функция полезности имеет вид: math. Цены товаров составляют: math и math. Доходы потребителя math. Во сколько раз должен измениться доход потребителя для компенсации увеличения цены всех товаров в два раза?
math4
math8
math2
math5
math8
math7
math200
2
Производственная функция фирмы: math. Известны цены на продукцию, капитал и рабочую силу: math. Найти во сколько раз затраты на увеличение капитала эффективнее увеличения затрат на рабочую силу (с точки зрения увеличения производства).
math1
math15
math5
math8
math2
math3
math0,5
Ответ введите с точностью до 3-го знака после запятой.
1,377
Пусть спрос (math) и предложение (math) линейные функции цены (math): d=a-bp; s=\alpha-\beta p. Скорость изменения цены: math. Решение этого уравнения имеет вид: math.
math16
math6
math3
math3
math1
math1
Найти цену (в долях от равновесной цены) через 3 постоянные времени. Ответ введите с точностью до 3-го знака после запятой.
0,980
Пусть производство инвестиционных товаров (math) зависит от нормы процента (math) линейно: math. Производство (math) определяется функцией Коба-Дугласа math, (math-занятая рабочая сила, math – используемый капитал). math, где math – производство потребительских товаров. math. Отсюда math. (Считать math=0,5.)
math1
math0,1
math0,4
math1
math0,02
math3
На сколько процентов уменьшится количество занятых, если math составит 1? Ответ введите с точностью до 1-го знака после запятой.
7,8
Пусть цена продукции на рынке зависит от объёмов её выпуска двумя фирмами (math) зависит следующим образом: math. Издержки фирм равны: math и math.
a20
b12
c4
d0,7
Найти суммарную прибыль в случае монополии. Ответ введите с точностью до 2-го знака после запятой.
3,93
Предлагается следующая модель инфляции. Денежная масса (math) зависит от процентной ставки (math) следующим образом: math. Производство определяется функцией Кобба-Дугласа: math. Цены: math, где math и math относятся к предыдущему периоду. Из math следует math.
M80
d100
f2
r10
A1
α0,5
L1
K7
Полагая прочие параметры неизменными, найти во сколько раз во второй период после изменения процентной ставки по сравнению с первым периодом после изменения процентной ставки изменятся цены, если процентная ставка уменьшится до 3. Ответ введите с точностью до 3-го знака после запятой.
1,621
Рассмотрим эволюторную модель прогресса. Пусть параметры функции Кобба-Дугласа меняются во времени: math. Затраты на научнотехнический прогресс составляют math.
math1
math0,1
math0,1
math0,4
math-0,05
math0,6
math0,4
В ответе укажите коэффициент прироста удельных затрат на научнотехнический прогресс. Ответ введите с точностью до 3-го знака после запятой.
-0,469
Дана зависимость от времени (math) курса ценной бумаги (math).
math12345678910
math1143911652473664876558001000
Найти во сколько раз среднее квадратичное отклонение уравнения линейной регрессии (math) меньше дисперсии уравнения квадратичной регрессии (math). Ответ введите с точностью до 1-го знака после запятой.
11,0
Дана неоклассическая производственная функция: math. Во сколько раз изменится math, если math увеличится в 1,5 раза? Ответ введите с точностью до 2-го знака после запятой.
1,23
Рассмотрим дифференциальную модель работы фирмы, являющейся главным поставщиком продукции на рынок. Цена продукции (math) зависит от объёма производства (math) следующим образом: math. Скорость прироста продукции (math) пропорциональна инвестициям (math): math. Выручка фирмы равна math. Норма инвестиций math. Инвестиции составляют math. Таким образом, math. Решением этого уравнения является логистическая функция: math, где math - объём производства в момент времени math. (В таблице исходных данных "math" - себестоимость.)
math120
math8
math0,5
math0,4
math10
math5
Во сколько раз увеличится прибыль за вычетом инвестиций к моменту времени t=1 если норму инвестирования уменьшить в два раза? Ответ введите с точностью до 1-го знака после запятой.
7,1
Пусть цена (math) зависит от предложения (math) следующим образом: math. Прибыль фирмы составляет величину: math. Скорость изменения объёма производства пропорциональна прибыли: math.
math7
math100
math0,03
math30
math0,1
math100
Найти методом Эйлера с шагом по t 0,1 значение объёма производства (y) для t=5. Затем найти методом Эйлера с шагом по t 0,05 значение объёма производства (y) для t=5. На сколько процентов изменился результат? Ответ введите с точностью до 3-го знака после запятой.
0,002
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,015
math0,25
math7
Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
10,3
Произведённые в год math товары (math) представлены потребительскими товарами (math) и инвестиционными (math): math. Инвестиции в год math зависят от прироста производства в прошлом году (math) по сравнению с позапрошлым (math): math. Потребление в год math зависит от выпуска продукции в прошлом году: math. Таким образом: math. Если положить math, то разностное уравнение принимает вид: math. Вид решения этого уравнения зависит от значений корней характеристического уравнения: math. Если это уравнение имеет единственное решение, то math. Если характеристическое уравнение имеет два различных корня (math и math), то math. (Считать, что math больше math) Если характеристическое уравнение имеет пару комплексно сопряжённых корней: math, где math – мнимая единица, то: math. Коэффициенты math и math могут быть определены из начальных условий для math и math.
math100
math110
math0,03
math0,25
math7
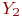Найти значение math. Ответ введите с точностью до 1-го знака после запятой.
38,4
Пусть объём производства (math) определяется функцией Кобба-Дугласа: math. При этом инвестируется доля продукта, совпадающая с показателем степени math. math, где: math – капитал, math – инвестиции, math – год, math – лаг инвестирования. Считать math и math постоянными. Найти отношение объёмов капитала при math для math и math. (math) Ответ введите с точностью до 2-го знака после запятой.
0,85
Дана неоклассическая производственная функция: Кобба-Дугласа: math. Во сколько раз изменится math, если math увеличится в 2 раза? Ответ введите с точностью до 2-го знака после запятой.
0,81
Задано линейное дифференциальное уравнение: math. Известно, что: math. Найти при каком значении math решение будет неустойчиво.
2
В экономике пять секторов. Известна матрица межотраслевых связей:
0,250,350,250,10,1
0,150,20,150,30,2
0,050,20,050,050,2
0,150,150,150,150,3
0,050,10,050,10,15
Конечное потребление по отраслям составляет:
5
6
2
8
6
Найти производство по отраслям.
(1)
64,97967
70,19194
39,00289
67,18347
38,95218
(2)
19,18457
21,33295
10,11776
21,18692
11,90789
(3)
33,2569
32,21004
15,83868
29,84722
17,24765
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Пусть math. Найти во сколько раз изменится удельное потребление, если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,98
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз увеличится удельное потребление при math если math увеличить в 2 раза. Ответ введите с точностью до 2-го знака после запятой.
0,40
Производство на одного работающего (в модели Кобба-Дугласа) равно: math. Оптимальная фондовооружённость с точки зрения максимума потребления на одного работающего равна math. Здесь использованы следующие обозначения: math – доля ВВП идущая на капитализацию; math – годовой темп прироста числа занятых; math – доля выбывших за год основных производственных фондов; math – коэффициент. Фондовооружённость, ниже которой её рост происходит ускоренно math. Пусть math. Найти во сколько раз (при увеличении math в два раза) изменится потребление на одного работающего. Ответ введите с точностью до 2-го знака после запятой.
0,40