Главная /
Математика /
Линейная алгебра
Линейная алгебра - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс посвящен изучению основных понятий и аппарата линейной алгебры.
Все ответы: Курс посвящен изучению основных понятий и аппарата линейной алгебры.
Какое доказательство, из ниже перечисленных, доказывает теорему:"Матрица проектора P в некотором базисе имеет вид ![math]() "?
"?
 "?
"?
(1) если ![math]() , то
, то ![math]() .
. ![math]() состоит из векторов
состоит из векторов ![math]() , т.е.
, т.е. ![math]() . Аналогично
. Аналогично ![math]() .
.
 , то
, то  .
.  состоит из векторов
состоит из векторов  , т.е.
, т.е.  . Аналогично
. Аналогично  .
.
(2) любой вектор ![math]() можно представить в виде
можно представить в виде ![math]() , где
, где ![math]() и
и ![math]() . Кроме того, если
. Кроме того, если ![math]() , то
, то ![math]() . В самом деле, тогда
. В самом деле, тогда ![math]() и
и ![math]() , поэтому
, поэтому ![math]() . Следовательно,
. Следовательно, ![math]() . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
 можно представить в виде
можно представить в виде  , где
, где  и
и  . Кроме того, если
. Кроме того, если  , то
, то  . В самом деле, тогда
. В самом деле, тогда  и
и  , поэтому
, поэтому  . Следовательно,
. Следовательно,  . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
(3) Выберем в пространстве W ортонормированный базис ![math]() . Рассмотрим вектор
. Рассмотрим вектор ![math]() . Условие
. Условие ![math]() означает, что , т.е.
означает, что , т.е. ![math]() . Выбрав такие числа
. Выбрав такие числа ![math]() , получим требуемый вектор
, получим требуемый вектор ![math]() .
.
 . Рассмотрим вектор
. Рассмотрим вектор  . Условие
. Условие  означает, что , т.е.
означает, что , т.е.  . Выбрав такие числа
. Выбрав такие числа  , получим требуемый вектор
, получим требуемый вектор  .
. Как называется функция ![math]() ?
?
 ?
?
(1) билинейной формой
(2) инвариантным подпространством
(3) билинейной матрицей
Как называется оператор ![math]() , если ?
, если ?
 , если ?
, если ?
(1) самосопряженным
(2) сопряженным линейному оператору ![math]()

(3) ортогональным
Какую матрицу имеет квадратичная форма ![math]() ?
?
 ?
?
(1)
(2)
(3)
Какие из матриц являются единичными?
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать однородные системы линейных уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Найти
det A, если
(1) 4
(2) 5
(3) 6
(4) -4
(5) -5
(6) -6
Ранг матрицы будет равен:
(1) 0
(2) 3
(3) 5
Какие операторы являются линейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Выберите верное утверждение:
(1) если ![math]() , то элементы x и y модуля с билинейной формой
, то элементы x и y модуля с билинейной формой ![math]() называют ортогональными
называют ортогональными
 , то элементы x и y модуля с билинейной формой
, то элементы x и y модуля с билинейной формой  называют ортогональными
называют ортогональными
(2) если для любых элементов x и y ![math]() , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
 , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
(3) если для каждого элемента x ![math]() , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической
 , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической Если матрицу транспонировать, то получится матрица ![math]() равная:
равная:
 равная:
равная:
(1)
(2)
(3)
Какое будет ортогональное преобразование неизвестных для квадратичной формы ![math]() , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
(1)
(2)
(3)
Выберите правильные свойства для
А, B и C - матриц, и чисел a и b
(1)
А+В=В+А
(2)
(А+В)+С=А+(В+С)
(3)
a(A)=(a)A
(4)
(a+b)A=aA+bA
(5)
a(А+В)=aА+aВ Среди предложенных матриц выбрать те, у которых ранг равен 3
(1)
(2)
(3)
(4)
(5)
(6)
Какие из матриц являются минорами матрицы
(1)
(2)
(3)
(4)
(5)
(6)
Какие матрицы, из ниже перечисленных, имеют ранг = 2?
(1)
(2)
(3)
Какие операторы являются нелинейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какое скалярное произведение будет иметь произвольные векторы ![math]() и
и ![math]() , при
, при ![math]() и
и ![math]() , при
, при ![math]() ?
?
 и
и  , при
, при  и
и  , при
, при  ?
?
(1) -1
(2) 4
(3) 0
Какая матрица, из ниже перечисленных, будет сопряженной матрицей, матрице
(1)
(2)
(3)
Какой индекс инерции будет иметь квадратичная форма ![math]() ?
?
 ?
?
(1) форма положительно определена
(2) каждый индекс инерции равен 2
(3) положительный индекс инерции равен 1, отрицательный индекс инерции равен 3
Выберите правильные свойства для
А и В - матриц, α - число
(1)
A(BC)=(AB)C
(2)
AB=BA
(3)
(A+B)C=AC+BC
(4)
A(B+C)=AB+AC
(5)
(αA)B=A(αB)
(6)
A2-B2=(A+B)(A-B) Дана система векторов. Какие из векторов входят в линейную оболочку указанной системы?
(1)
![math]()

(2)
(3)
(4)
(5)
(6)
Выбрать алгебраические дополнения для
(1)
(2)
(3)
(4)
(5)
(6)
Какие, из следующих отображений в соответствующих векторных пространствах являются линейными операторами?
(1) ![math]() (a - фиксированный вектор)
(a - фиксированный вектор)
 (a - фиксированный вектор)
(a - фиксированный вектор)
(2) ![math]() (a - фиксированный вектор)
(a - фиксированный вектор)
 (a - фиксированный вектор)
(a - фиксированный вектор)
(3) ![math]() (a - фиксированный вектор)
(a - фиксированный вектор)
 (a - фиксированный вектор)
(a - фиксированный вектор)
(4) ![math]() (V - евклидово пространство, a,b - фиксированные векторы)
(V - евклидово пространство, a,b - фиксированные векторы)
 (V - евклидово пространство, a,b - фиксированные векторы)
(V - евклидово пространство, a,b - фиксированные векторы)
(5) ![math]() (V - евклидово пространство, a - фиксированные векторы)
(V - евклидово пространство, a - фиксированные векторы)
 (V - евклидово пространство, a - фиксированные векторы)
(V - евклидово пространство, a - фиксированные векторы) Оператор Будет оператором:
(1) проецирования на ось ОХ
(2) отражения относительно плоскости YOZ
(3) поворота относительно оси OX
Каким вектором можно дополнить систему векторов: до ортогонального базиса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите верные утверждения:
(1) всякую комплексную матрицу С (с элементами ![math]() ) можно представить в виде
) можно представить в виде ![math]()
 ) можно представить в виде
) можно представить в виде 
(2) если все элементы матрицы А действительные числа, то сопряженная матрица совпадает с транспонированной, т.е. ![math]()

(3) квадратная матрица А называется эрмитовой, если ![math]()

Как будет выглядеть квадратичная форма ![math]() , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?
 , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?
(1) ![math]()

(2) ![math]()

(3)
Сумма каких матриц равна ?
(1)
(2)
(3)
(4)
(5)
(6)
Для прямоугольных матриц
В и С и квадратной матрицы А=ВС верно
(1) если у
В линейно независимые
строки, а у С линейно независимы столбцы, то А - невырожденная
(2) если у
С линейно независимые
строки, а у В линейно независимы столбцы, то А - невырожденная
(3) если у
В линейно независимы строки, то rank A = rank C Выбрать четные перестановки
(1) (1,2,3,4)
(2) (1,3,2,4)
(3) (1,4,3,2)
(4) (1,4,2,3)
(5) (3,2,4,1)
(6) (3,4,2,1)
Какую матрицу будет иметь оператор в пространстве ![math]() в базисе из единственных векторов?
в базисе из единственных векторов?
 в базисе из единственных векторов?
в базисе из единственных векторов?
(1)
(2)
(3)
Какое собственное значение будет иметь матрица порядка n.
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе ![math]() , где
, где ![math]() ?
?
 - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе  , где
, где  ?
?
(1)
(2)
(3)
Какое ядро отображения будет иметь матрица
(1) ker A=2
(2) ker A=0
(3) ker A=1
Какое треугольное разложение будет иметь матрица при формуле ![math]() ?
?
 ?
?
(1)
(2)
(3)
Чему равно произведение матриц
(1)
(2)
(3)
(4)
(5)
(6)
Для двух линейных подпространств
L1 и L2
заданы базисы. Выбрать удовлетворяющие условию dim ( L1 + L2 ) = 6
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать правильные утверждения для квадратных матриц
(1) у любой матрицы можно вычислить детерминант
(2) если матрица невырожденная, то детерминант неравен нулю
(3) если детерминант равен нулю, то матрица вырожденная
(4) у любой матрицы
det(A)=det(AT)
(5) не существует матрицы, у которой
det(A)=det(A)
(6) для любых матриц
A и B верно det(AB)=det(A)det(B) Матрица будет иметь оператор:
(1) поворота плоскости на угол ![math]() в произвольном ортонормированном базисе
в произвольном ортонормированном базисе
 в произвольном ортонормированном базисе
в произвольном ортонормированном базисе
(2) проектирования трехмерного пространства на координптную ось вектора ![math]() параллельно координатной плоскости векторов
параллельно координатной плоскости векторов ![math]() и
и ![math]() в базисе
в базисе ![math]()
 параллельно координатной плоскости векторов
параллельно координатной плоскости векторов  и
и  в базисе
в базисе 
(3) ![math]() в пространстве
в пространстве ![math]() в базисе из матричных единиц
в базисе из матричных единиц
 в пространстве
в пространстве  в базисе из матричных единиц
в базисе из матричных единиц Выберите верные утверждения:
(1) ортогональную матрицу Q можно определить как такую матрицу, для которой транспонированная матрица ![math]() равна обратной матрице
равна обратной матрице ![math]()
 равна обратной матрице
равна обратной матрице 
(2) квадратная матрица Q тогда и только тогда будет ортогональной, если сумма квадратов всех элементов любой ее стороны равна 0, а сумма произведений соответственных элементов любых двух ее различных строк равна 1
(3) квадратная матрица Q тогда и только тогда будет ортогональной, если сумма квадратов всех элементов любой ее стороны равна 1, а сумма произведений соответственных элементов любых двух ее различных строк равна 0
Какой ортогональный базис подпространства, натянутого на систему векторов будет, если применить процесс ортогонализации?
(1)
(2)
(3)
Базис ядра: ![math]() будет иметь матрица:
будет иметь матрица:
 будет иметь матрица:
будет иметь матрица:
(1)
(2)
(3)
Как будет выглядеть невырожденное линейное преобразование, которое приводит квадратичные формы к каноническому виду?
(1) матрицы форм F и G перестановочны . Ортогональное преобразование неизвестных приводит форму к каноническуому виду ![math]() , а форму G - к каноническому виду
, а форму G - к каноническому виду ![math]()
 , а форму G - к каноническому виду
, а форму G - к каноническому виду 
(2) форма F положительно определена. Преобразование неизвестных приводит форму F к нормальному виду, а форму G - к каноническому виду ![math]()

(3) форма F отрицательно определена. Преобразование неизвестных приводят форму F к нормальному виду, а форму G - к каноническому виду ![math]()

Какая из матриц является диагональной?
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать ошибочные наборы векторов, составляющих базис
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать правильные утверждения
(1) существует ненулевая матрица перестановка столбцов которой не изменяет ее детерминанта
(2)
det(A)=ndet(A), где n-размерность матрицы А
(3)
Пусть линейный оператор в пространстве ![math]() в базисе
в базисе ![math]() имеет матрицу Какая будет матрица этого оператора в базисе
имеет матрицу Какая будет матрица этого оператора в базисе ![math]() ?
?
 в базисе
в базисе  имеет матрицу Какая будет матрица этого оператора в базисе
имеет матрицу Какая будет матрица этого оператора в базисе  ?
?
(1)
(2)
(3)
Какое доказательство, из ниже переичсленных, доказывает, что для нормального оператора в унитарном пространстве существует ортонормированный базис из собственных векторов?
(1) пусть ![math]() . Тогда
. Тогда ![math]() и . Следовательно,
и . Следовательно, ![math]() .
.
 . Тогда
. Тогда  и . Следовательно,
и . Следовательно,  .
.
(2) инвариантное подпространство для нормального оператора инвариантно и для сопряженного и ограничение нормального оператора на инвариантном подпространстве нормально. Поэтому, пространство можно разбивать в прямую ортогональную сумму инвариантных подпространств до тех пор, пока не придем к одномерным подпространствам.
(3) для любой нормальной матрицы А существует унитарная матрица С такая, что ![math]() диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
 диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов. Какая будет ортогональная проекция и перпендикуляр, опущенный из вектора x на подпространство L, при условиях, что ![math]() , L натянутую на векторы
, L натянутую на векторы
 , L натянутую на векторы
, L натянутую на векторы
(1) ![math]()

(2) ![math]()

(3) ![math]()

В пространстве многочленов ![math]() задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора ![math]() в базисе
в базисе ![math]() ?
?
 задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора  в базисе
в базисе  ?
?
(1)
(2)
(3)
Какие квадратные формы, из ниже перечисленных, будут отрицательно определены?
(1)
(2) ![math]()

(3) ![math]()

Какие из приведенных коэффициентов доказывают линейную зависимость (независимость) векторов
(1) 1, 2, 3, 0
(2) 1, 2, 3, -1
(3) 0, 0, 0, 0
(4) 3, 2, 1, 1
(5) 2, 4, 6, -2
(6) 2, 4, 6, 0
Определить, является ли линейным заданное подпространство для указанного пространства?
(1) Линейное пространство определено как всевозможные системы
действительных чисел
х=(х1,х2,х3). Сложение и умножение на число определены как
x+y=(x1+y1,x2+y2,x3+y3) ax=(ax1,ax2,ax3). Подпространство определено как
z=(0,z1,z2)
(2) Линейное пространство определено, как множество
геометрических векторов. Подпространство - множество векторов с началом в начале
координат и лежащих в первом октанте
(3) Линейное пространство определено как всевозможные многочлены не выше пятой степени.
Подпространство - многочлены вида
a0t5+a1t3+a3 Найти собственные числа матрицы
(1) 4
(2) 5
(3) 6
(4) 7
(5) 8
(6) 9
Какие подпространства, из перечисленных ниже, являются инвариантными подпространствами для оператора дифференцирования в пространстве ![math]() ?
?
 ?
?
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]()

(3) ![math]()

Доказательство, какого следствия приведено ниже: Если ![math]() - угол между вектором
- угол между вектором ![math]() и подпространством W, то
и подпространством W, то ![math]() ?
?
 - угол между вектором
- угол между вектором  и подпространством W, то
и подпространством W, то  ?
?
(1) ![math]() причем равенство достигается только при
причем равенство достигается только при ![math]()
 причем равенство достигается только при
причем равенство достигается только при 
(2)
(3) для ортогональных векторов ![math]() в
в ![math]() m-мерное подпространство W, образующее с ними данные углы
m-мерное подпространство W, образующее с ними данные углы ![math]() , существует тогда и только тогда, когда при i=1,...,n.
, существует тогда и только тогда, когда при i=1,...,n.
 в
в  m-мерное подпространство W, образующее с ними данные углы
m-мерное подпространство W, образующее с ними данные углы  , существует тогда и только тогда, когда при i=1,...,n.
, существует тогда и только тогда, когда при i=1,...,n. Какой биортогональный базис будет иметь базис пространства ![math]() :
:
 :
:
(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Матрицей квадратичной формы называется:
(1) вырожденная матрица ![math]()

(2) невырожденная матрица ![math]()

(3) симметричная матрица ![math]() , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы
 , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы Вычислить значение
2С-АВ, если
(1)
(2)
(3)
(4) в данном случае произвести расчет нельзя,
матрицы не согласованы по числу строк и столбцов
Линейное пространство определено как всевозможные многочлены не выше пятой степени.
Подпространство
R1 - многочлены вида
a0t4+a1t2+a3
Подпространство R2 - многочлены вида b0t+b1.
Найти R3=R1∩R2 и R4=R1+R2
(1)
R1+R2 =a0t4+a1t2+a2t+a3
(2)
R1+R2 =a0t4+a1t3+a2t2+a3t+a4
(3)
R1∩R2=a
(4)
R1∩R2 пустое множество
(5)
R1+R2 все пространство Какие из векторов являются собственными для характеристического
числа
=7 матрицы
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определите подпространства в трехвекторном пространстве, инвариантные относительно линейного оператора с матрицей
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4)
(5) ![math]()

Как будет выглядеть матрица X в уравнении
(1)
(2)
(3)
Какой угол будет между векторами ![math]() ,
, ![math]() ?
?
 ,
,  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Квадратный корень будет иметь матрица:
(1)
(2)
(3)
Как будет выглядеть кососимметрическая билинейная функция ![math]() , если привести ее к каноническому виду?
, если привести ее к каноническому виду?
 , если привести ее к каноническому виду?
, если привести ее к каноническому виду?
(1)
(2)
(3)
Дана система из n векторов, содержащих m строк. Ранг системы определяется как
(1) минимальное из чисел n и m
(2) максимальное из чисел n и m
(3) максимальное количество линейно
независимых векторов, которые из нее можно выделить
(4) максимальное количество линейно
независимых строк в матрице, составленной из векторов
(5) максимальное количество линейно
независимых столбцов в матрице, составленной из векторов
(6) произведение nm
Найти базис
B и размерность подпространства
L решений линейной однородной системы уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать верные высказывания
(1) не существует матрицы 3х3, у которой любые две
строки линейно независимы, а три зависимы
(2)
det(A-I)=0 равносильно
существованию ненулевого решения для системы (A-I)х=0
(3) пусть характеристическое уравнение
(-1)
n n+...+det(A)=0, имеет только вещественные
корни, то они различные и их количество равно n
(4) геометрическая кратность корня
характеристического уравнения не превосходит алгебраическую кратность
Какие имеет собственные векторы и значения оператор дифференцирования в пространстве ![math]() ?
?
 ?
?
(1) многочлены нулевой степени
(2) одночлены
(3) ![math]()

Какая матрица, является обратной матрице
(1)
(2)
(3)
Какие будут косинусы внутренних углов треугольника ABC, заданного координатами вершин ![math]() ,
, ![math]() ,
, ![math]() ?
?
 ,
,  ,
,  ?
?
(1)
(2)
(3)
При возведении матрицы в степень 3, получиться матрица:
(1)
(2)
(3)
Какое уравнение поверхностей 2-го порядка будет иметь канонический вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти координаты вектора в базисе
(1) 1, 0, 1
(2) 0, 1, 0
(3) 1, 1, 0
(4) 0, 1, 1
(5) 1, 1, 1
(6) 1, 0, 0
Найти общее решение и одно частное решение системы уравнений
(1) общее решение
х1=(х3-3х4-2)/7
х2=(7х4+х3+3)/9
(2) общее решение
х3=(х1-9х2-2)/11
х4=(-5х1+х2+10)/11
(3) общее решение
х1=(5х2-6х4-2)
х3=(5х2+8х4+2)
(4) частное решение
(0,1,1,-1)
(5) частное решение
(1,0,-1,1)
(6) частное решение
(0,1,-1,1) Найти производную от
det(A) по х, если
(1)
x4+3x3+2x2+x+1
(2)
x4+2x2+1
(3)
x4+2x2
(4)
3x3+x+1
(5)
3x3+x
(6) 0
Пусть ![math]() - линейное преобразование пространства
- линейное преобразование пространства ![math]() . Линейное подпространство
. Линейное подпространство ![math]() называется инвариантным относительно
называется инвариантным относительно ![math]() , если:
, если:
 - линейное преобразование пространства
- линейное преобразование пространства 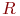 . Линейное подпространство
. Линейное подпространство  называется инвариантным относительно
называется инвариантным относительно  , если:
, если:
(1) для любого ![math]()

(2) для любого ![math]() и
и ![math]()
 и
и 
(3) для каждого вектора X из ![math]() вектор Ax также принадлежит
вектор Ax также принадлежит ![math]()
 вектор Ax также принадлежит
вектор Ax также принадлежит 
Чему будет равен ранг матрицы
(1) 3
(2) 2
(3) 6
Какой будет угол между вектором ![math]() и линейным подпространством натянутым на векторы
и линейным подпространством натянутым на векторы
 и линейным подпространством натянутым на векторы
и линейным подпространством натянутым на векторы
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие собственные значения будет иметь матрица
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая квадратичная форма, из ниже перечисленных, будет иметь вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Транспонированная матрица обладает свойствами
(1)
(AT )T =A
(2)
(AB)T=ATBT
(3)
(A+B)T=AT+BT
(4)
(αA)T=αAT
(5) число строк всегда равно числу столбцов
(6) на диагонали обязательно найдется ненулевой элемент
Найти общее решение в зависимости от параметра
(1) при ![math]() система несовместна
система несовместна
 система несовместна
система несовместна
(2) при ![math]() система несовместна
система несовместна
 система несовместна
система несовместна
(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть матрицы
А и В такие, что их
элементы связваны соотношением аij≥bij≥0, то
(1)
det(A)≥det(B)
(2)
det(B)≥det(A)
(3)
det(A+B)≥det(B)
(4)
det(A)≥det(A-B) Если ![math]() , то
, то ![math]() . Приведенное выше доказательство, доказывает, что:
. Приведенное выше доказательство, доказывает, что:
 , то
, то  . Приведенное выше доказательство, доказывает, что:
. Приведенное выше доказательство, доказывает, что:
(1) если оператор ![math]() имеет собственное значение
имеет собственное значение ![math]() , то одно из чисел
, то одно из чисел ![math]() и
и ![math]() является собственным значением оператора
является собственным значением оператора ![math]()
 имеет собственное значение
имеет собственное значение  , то одно из чисел
, то одно из чисел  и
и  является собственным значением оператора
является собственным значением оператора 
(2) в пространстве ![math]() линейный оператор
линейный оператор ![math]() имеет множество собственных значений
имеет множество собственных значений ![math]()
 линейный оператор
линейный оператор  имеет множество собственных значений
имеет множество собственных значений 
(3) если оператор ![math]() невырожденный, то операторы
невырожденный, то операторы ![math]() и
и ![math]() имеют одни и те же собственные векторы
имеют одни и те же собственные векторы
 невырожденный, то операторы
невырожденный, то операторы  и
и  имеют одни и те же собственные векторы
имеют одни и те же собственные векторы Какая система линейных уравнений, из ниже перечисленных, не имеет решений?
(1)
(2)
(3)
Линейное преобразование ![math]() в базисе
в базисе ![math]() имеет матрицу . Как будет выглядеть матрица этого же преобразования в базисе:
имеет матрицу . Как будет выглядеть матрица этого же преобразования в базисе: ![math]() ?
?
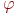 в базисе
в базисе  имеет матрицу . Как будет выглядеть матрица этого же преобразования в базисе:
имеет матрицу . Как будет выглядеть матрица этого же преобразования в базисе:  ?
?
(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Какой канонический вид будут иметь уравнения поверхностей второго порядка ![math]() ?
?
 ?
?
(1)
(2)
(3)
Примерами линейного пространства являются
(1) квадратные матрицы одной размерности
(2) диагональные матрицы одной размерности
(3) единичные матрицы одной размерности
(4) нулевые матрицы одной размерности
(5) ненулевые матрицы одной размерности
Выбрать верные утверждения
(1) если
l1...lk
различные собственные числа матрицы А и х1...хk
- соответствующие им собственные вектора, то х1...хk - линейно независимы
(2) собственные числа матриц
А и А-1 не совпадают
(3) собственные вектора матриц
А и А-1 совпадают Многочленной матрицей называется:
(1) матрица, элементами которой являются многочлены переменной ![math]()

(2) матрица ![math]() n-го порядка, элементы которой вычисляются по формуле:
n-го порядка, элементы которой вычисляются по формуле: ![math]()
 n-го порядка, элементы которой вычисляются по формуле:
n-го порядка, элементы которой вычисляются по формуле: 
(3) ![math]() - матрица
- матрица ![math]() , если
, если ![math]()
 - матрица
- матрица  , если
, если 
Какое доказательство, из ниже перечисленных, доказывает теорему:"Если P-проектор, I-P - тоже проектор, причем Ker (I-P)=Im P и Im (I-P")=Ker P"?
(1) если ![math]() , то
, то ![math]() .
. ![math]() состоит из векторов
состоит из векторов ![math]() , т.е.
, т.е. ![math]() . Аналогично
. Аналогично ![math]() .
.
 , то
, то  .
.  состоит из векторов
состоит из векторов  , т.е.
, т.е.  . Аналогично
. Аналогично  .
.
(2) любой вектор ![math]() можно представить в виде
можно представить в виде ![math]() , где
, где ![math]() и
и ![math]() . Кроме того, если
. Кроме того, если ![math]() , то
, то ![math]() . В самом деле, тогда
. В самом деле, тогда ![math]() и
и ![math]() , поэтому
, поэтому ![math]() . Следовательно,
. Следовательно, ![math]() . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
 можно представить в виде
можно представить в виде  , где
, где  и
и  . Кроме того, если
. Кроме того, если  , то
, то  . В самом деле, тогда
. В самом деле, тогда  и
и  , поэтому
, поэтому  . Следовательно,
. Следовательно,  . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
(3) Выберем в пространстве W ортонормированный базис ![math]() . Рассмотрим вектор
. Рассмотрим вектор ![math]() . Условие
. Условие ![math]() означает, что , т.е.
означает, что , т.е. ![math]() . Выбрав такие числа
. Выбрав такие числа ![math]() , получим требуемый вектор
, получим требуемый вектор ![math]() .
.
 . Рассмотрим вектор
. Рассмотрим вектор  . Условие
. Условие  означает, что , т.е.
означает, что , т.е.  . Выбрав такие числа
. Выбрав такие числа  , получим требуемый вектор
, получим требуемый вектор  .
. Если ![math]() является билинейной формой, то пара
является билинейной формой, то пара ![math]() называется:
называется:
 является билинейной формой, то пара
является билинейной формой, то пара  называется:
называется:
(1) билинейной функцией
(2) модулем с билинейной формой
(3) билинейной формой на свободном модуле
Как называется оператор ![math]() , если ?
, если ?
 , если ?
, если ?
(1) самосопряженным
(2) сопряженным линейному оператору ![math]()

(3) ортогональным
Какую матрицу имеет квадратичная форма ![math]() ?
?
 ?
?
(1)
(2)
(3)
Какие из матриц являются единичными?
(1)
(2)
(3)
(4)
(5)
Выбрать неоднородные системы линейных уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Найти
det A, если
(1) 4
(2) 5
(3) 6
(4) -4
(5) -5
(6) -6
Ранг матрицы будет равен:
(1) 2
(2) 1
(3) 4
Какие операторы являются линейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Выберите не верные утверждения:
(1) если ![math]() , то элементы x и y модуля с билинейной формой
, то элементы x и y модуля с билинейной формой ![math]() называют ортогональными
называют ортогональными
 , то элементы x и y модуля с билинейной формой
, то элементы x и y модуля с билинейной формой  называют ортогональными
называют ортогональными
(2) если для любых элементов x и y ![math]() , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
 , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
(3) если для каждого элемента x ![math]() , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической
 , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической Если матрицу транспонировать, то получится матрица ![math]() равная:
равная:
 равная:
равная:
(1)
(2)
(3)
Какое будет ортогональное преобразование неизвестных для квадратичной формы ![math]() , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
(1)
(2)
(3)
Какие из утверждений верные?
(1) сложение матриц обладает свойством ассоциативности
(2) сложение матриц А + B определено только в том случае,
если матрица А имеет размерность mxn, а В nxk
(3) сложение матриц А + B определено только в том случае,
если размерности матриц А и В совпадают
Среди предложенных матриц выбрать те, у которых ранг равен 2
(1)
(2)
(3)
(4)
(5)
(6)
Какие из матриц являются минорами матрицы
(1)
(2)
(3)
(4)
(5)
(6)
Какие матрицы, из ниже перечисленных, имеют ранг = 3?
(1)
(2)
(3)
Какие операторы являются нелинейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какое скалярное произведение будет иметь произвольные векторы ![math]() и
и ![math]() , при
, при ![math]() и
и ![math]() , при
, при ![math]() ?
?
 и
и  , при
, при  и
и  , при
, при  ?
?
(1) -1
(2) 4
(3) 0
Какая матрица, из ниже перечисленных, будет сопряженной матрицей, матрице
(1)
(2)
(3)
Какой индекс инерции будет иметь квадратичная форма ![math]() ?
?
 ?
?
(1) форма положительно определена
(2) каждый индекс инерции равен 2
(3) положительный индекс инерции равен 1, отрицательный индекс инерции равен 3
Какое из утверждений верное?
(1) умножение матриц
АB определено только в том случае, если матрица А имеет размерность m x n, а В - n x m
(2) умножение матриц
АB определено только в том случае, если количество строк в матрице А соответствует количеству столбцов в матрице B
(3) умножение матриц
АB определено только в том случае, если количества элементов в матрицах совпадают Дана система векторов. Какие из векторов входят в линейную оболочку указанной системы?
(1)
![math]()

(2)
(3)
(4)
(5)
(6)
Выбрать алгебраические дополнения для
(1)
(2)
(3)
(4)
(5)
(6)
Какие, из следующих отображений в соответствующих векторных пространствах являются линейными операторами?
(1) ![math]() (a,b - фиксированные числа)
(a,b - фиксированные числа)
 (a,b - фиксированные числа)
(a,b - фиксированные числа)
(2) ![math]()

(3) ![math]()

Оператор Будет оператором:
(1) отражения относительно плоскости y-z=0
(2) поворота относительно оси OZ
(3) проецирования на плоскость y+z=0
Каким вектором можно дополнить систему векторов: до ортогонального базиса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите не верные утверждения:
(1) всякую комплексную матрицу С (с элементами ![math]() ) можно представить в виде
) можно представить в виде ![math]()
 ) можно представить в виде
) можно представить в виде 
(2) если все элементы матрицы А действительные числа, то сопряженная матрица совпадает с транспонированной, т.е. ![math]()

(3) квадратная матрица А называется эрмитовой, если ![math]()

Какие преобразования переменных позволят привести квадратичную форму ![math]() к нормальному виду?
к нормальному виду?
 к нормальному виду?
к нормальному виду?
(1) ![math]()

(2) ![math]()

(3)
Сумма каких матриц равна ?
(1)
(2)
(3)
(4)
(5)
(6)
Для прямоугольных матриц
В и С и квадратной матрицы А=ВС верно
(1) если у
С линейно независимы строки, то rank A = rank В
(2) если у
А линейно независимы строки, то у В и С линейно независимы столбцы
(3) если у
А линейно зависимы строки, то у В или С линейно зависимы столбцы Выбрать нечетные перестановки
(1) (1,2,4,3)
(2) (1,3,5,4)
(3) (4,1,3,2)
(4) (1,4,3,2)
(5) (3,4,2,1)
(6) (4,3,2,1)
Какую матрицу будет иметь оператор в пространстве ![math]() в базисе из матричных единиц?
в базисе из матричных единиц?
 в базисе из матричных единиц?
в базисе из матричных единиц?
(1)
(2)
(3)
Какое собственное значение будет иметь матрица порядка n.
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе ![math]() ?
?
 - ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе
- ортонормированный базис евклидова пространства. Какое выражение будет для скалярного произведения прозвольных векторов x и y через их координаты в базисе  ?
?
(1)
(2)
(3)
Какое ядро отображения будет иметь матрица
(1) базис ядра: ![math]()

(2) базис ядра: ![math]()

(3) базис ядра: ![math]()

Какое треугольное разложение будет иметь матрица при формуле ![math]() ?
?
 ?
?
(1)
(2)
(3)
Чему равно произведение матриц
(1)
(2)
(3)
(4)
(5)
(6)
Для двух линейных подпространств
L1 и L2
заданы базисы. Выбрать удовлетворяющие условию dim ( L1 + L2 ) = 4
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать правильные утверждения
(1) если матрица неквадратная, то ее детерминант отличен от нуля
(2) если матрица неквадратная, то ее детерминант равен нулю
(3) у любой матрицы можно вычислить детерминант
(4) для диагональной матрицы можно найти детерминант
(5) для любых матриц
A и B верно det(AB)=det(A)det(B)
(6) детерминант вырожденной квадратной матрицы равен нулю
Матрицу будет иметь оператор:
(1) ![math]() (A, B - фиксированные матрицы) в пространстве
(A, B - фиксированные матрицы) в пространстве ![math]() в базисе, состоящем из матричных единиц
в базисе, состоящем из матричных единиц
 (A, B - фиксированные матрицы) в пространстве
(A, B - фиксированные матрицы) в пространстве  в базисе, состоящем из матричных единиц
в базисе, состоящем из матричных единиц
(2) дифференцирования в пространстве ![math]() в базисе
в базисе ![math]()
 в базисе
в базисе 
(3) в пространстве ![math]() в базисе из матричных единиц
в базисе из матричных единиц
 в базисе из матричных единиц
в базисе из матричных единиц Выберите не верные утверждения:
(1) ортогональную матрицу Q можно определить как такую матрицу, для которой транспонированная матрица ![math]() равна обратной матрице
равна обратной матрице ![math]()
 равна обратной матрице
равна обратной матрице 
(2) квадратная матрица Q тогда и только тогда будет ортогональной, если сумма квадратов всех элементов любой ее стороны равна 0, а сумма произведений соответственных элементов любых двух ее различных строк равна 1
(3) квадратная матрица Q тогда и только тогда будет ортогональной, если сумма квадратов всех элементов любой ее стороны равна 1, а сумма произведений соответственных элементов любых двух ее различных строк равна 0
Какой ортогональный базис подпространства, натянутого на систему векторов будет, если применить процесс ортогонализации?
(1)
(2)
(3)
Базис ядра: ![math]() будет иметь матрица:
будет иметь матрица:
 будет иметь матрица:
будет иметь матрица:
(1)
(2)
(3)
Как будет выглядеть невырожденное линейное преобразование, которое приводит квадратичные формы к каноническому виду?
(1) матрицы форм F и G перестановочны . Ортогональное преобразование неизвестных приводит форму к каноническуому виду ![math]() , а форму G - к каноническому виду
, а форму G - к каноническому виду ![math]()
 , а форму G - к каноническому виду
, а форму G - к каноническому виду 
(2) форма F положительно определена. Преобразование неизвестных приводит форму F к нормальному виду, а форму G - к каноническому виду ![math]()

(3) форма F отрицательно определена. Преобразование неизвестных приводят форму F к нормальному виду, а форму G - к каноническому виду ![math]()

Диагональная матрица обладает свойствами
(1) на диагонали стоят только 1
(2) на диагонали стоят только одинаковые элементы
(3) на диагонали стоят только отличные от 0 элементы
(4) на диагонали всегда найдутся ненулевые элементы
(5) вне диагонали стоят только 0
(6) всегда число строк и столбцов совпадает
Выбрать наборы векторов, которые могут составлять базис
(1)
(2)
(3)
(4)
(5)
(6)
(1) если после перстановки столбцов матрицы детерминант не изменился, то матрица - вырожденная
(2) если столбец матрицы умножить на число, то детерминант умножится на то же самое число
(3)
det(-A)=-det(A) Пусть линейный оператор в пространстве ![math]() имеет в базисе
имеет в базисе ![math]() матрицу Какая будет его матрица в базисе
матрицу Какая будет его матрица в базисе ![math]() ?
?
 имеет в базисе
имеет в базисе  матрицу Какая будет его матрица в базисе
матрицу Какая будет его матрица в базисе  ?
?
(1)
(2)
(3)
Какое доказательство, из ниже переичсленных, доказывает, что ортогональность собственных векторов нормального оператора в унитарном пространстве, принадлежит различным собственным значениям?
(1) пусть ![math]() . Тогда
. Тогда ![math]() и . Следовательно,
и . Следовательно, ![math]() .
.
 . Тогда
. Тогда  и . Следовательно,
и . Следовательно,  .
.
(2) инвариантное подпространство для нормального оператора инвариантно и для сопряженного и ограничение нормального оператора на инвариантном подпространстве нормально. Поэтому, пространство можно разбивать в прямую ортогональную сумму инвариантных подпространств до тех пор, пока не придем к одномерным подпространствам.
(3) для любой нормальной матрицы А существует унитарная матрица С такая, что ![math]() диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
 диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов. Какая будет ортогональная проекция и перпендикуляр, опущенный из вектора x на подпространство L, при условиях, что ![math]() , L натянутую на векторы
, L натянутую на векторы
 , L натянутую на векторы
, L натянутую на векторы
(1) ![math]()

(2) ![math]()

(3) ![math]()

В пространстве многочленов ![math]() задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора ![math]() в базисе
в базисе
 задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора  в базисе
в базисе
(1)
(2)
(3)
Какие квадратные формы, из ниже перечисленных, будут положительно определены?
(1) ![math]()

(2) ![math]()

(3)
Какие из приведенных коэффициентов доказывают линейную зависимость векторов
(1) 1, 1, -1, 2, 1
(2) 1, 1, -1, 0, 1
(3) 1, 1, 0, -1, 0
(4) 0, 1, 1, 1, -1
(5) 0, 1, 0, -1, 1
(6) 0, 0, -1, 1, -1
Определить, является ли линейным заданное подпространство для указанного пространства?
(1) Линейное пространство определено, как множество
геометрических векторов. Подпространство - множество векторов с началом в начале
координат и лежащих в первом или седьмом октанте (октанты расположено центрально симметрично)
(2) Линейное пространство - точки 1 октанта, не лежащие на координатных плоскостях.
Сложение точек
Р1=(х1,y1,z1) Р2=(x2,y2,z2) определено как Р1+Р2=(x1x2,y1y2,z1z2),
умножение на число P=(x, y, z.
Подпространство - множество точек на плоскости z=1
(3) Линейное пространство определено, как множество
геометрических векторов. Подпространство - множество векторов
a=Xi+Yj+Zk, где X,Y,Z - рациональные числа? Найти собственные числа матрицы
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5
(6) 6
Какие подпространства, из перечисленных ниже, являются инвариантными подпространствами для линейного оператора, имеющего в некотором базисе матрицу, состоящую из одной жордановой клетки?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Доказательство, какого следствия приведено ниже: вектор ![math]() ортогонален всему пространству V.
ортогонален всему пространству V.
 ортогонален всему пространству V.
ортогонален всему пространству V.
(1) если ![math]() - ортонормированный базис пространства V и
- ортонормированный базис пространства V и ![math]() , то
, то ![math]()
 - ортонормированный базис пространства V и
- ортонормированный базис пространства V и  , то
, то 
(2) если w и ![math]() - ортогональные проекции вектора
- ортогональные проекции вектора ![math]() на подпространства W и
на подпространства W и ![math]() , то
, то ![math]()
 - ортогональные проекции вектора
- ортогональные проекции вектора  на подпространства W и
на подпространства W и  , то
, то 
(3)
Какой биортогональный базис будет иметь базис пространства ![math]()

(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Невырожденной квадратичной формой называется:
(1) невырожденная матрица ![math]()

(2) вырожденная матрица ![math]()

(3) симметричная матрица ![math]() , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы
 , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы Вычислить значение
2C+АВ, если
(1)
(2)
(3)
(4)
(5)
(6) В данном случае произвести расчет нельзя,
матрицы не согласованы по числу строк и столбцов
Линейное пространство определено, как множество
геометрических векторов.
R1 - множество векторов, параллельных
плоскости ОXY R2 - множество векторов, параллельных
плоскости ОXZ. Найти R3=R1∩R2 и R4=R1+R2
(1)
R3 - множество векторов параллельных оси ОХ
(2)
R3 - множество векторов параллельных оси ОY
(3)
R3 - множество векторов параллельных оси ОZ
(4)
R3 - пустое
(5)
R4 - все пространство
(6)
R4 - множество векторов параллельных плоскости ОYZ Какие из векторов являются собственными для характеристического
числа
=-2 матрицы
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определите, какие подпространства в ![math]() и
и ![math]() , инвариантные относительно оператора
, инвариантные относительно оператора ![math]() :
:
 и
и  , инвариантные относительно оператора
, инвариантные относительно оператора  :
:
(1) ![math]()

(2) линейная оболочка любого множества одночленов степени не выше ![math]()

(3)
(4)
Как будет выглядеть матрица X в уравнении
(1)
(2)
(3)
Какой угол будет между векторами ![math]() ,
, ![math]() ?
?
 ,
,  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Квадратный корень будет иметь матрица:
(1)
(2)
(3)
Определить ![math]() , если
, если
 , если
, если
(1) 0
(2) 1
(3) 2
(4) 3
(5) 4
Найти базис
B и размерность подпространства L решений линейной однородной системы уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать верные высказывания для матрицы
А и многочлена
p(A)=a 0I + a 1A +...+ a mA m
(1) собственные вектора
А являются собственными векторами р(А)
(2) собственные числа
р(А) являются собственными числами А
(3) собственные числа
А являются собственными числами р(А)
(4) геометрическая кратность корней
р(А) может быть больше геометрической кратности корней А Какие имеет собственные векторы и значения оператор ![math]() в пространстве
в пространстве ![math]() ?
?
 в пространстве
в пространстве  ?
?
(1) ![math]()

(2) одночлены
(3) ![math]()

Какая матрица, является обратной матрице
(1)
(2)
(3)
Какие будут косинусы углов между прямой ![math]() и осями координат?
и осями координат?
 и осями координат?
и осями координат?
(1) ![math]()

(2) ![math]()

(3) ![math]()

При возведении матрицы в степень 2, получиться матрица:
(1)
(2)
(3)
Какое уравнение поверхностей 2-го порядка будет иметь канонический вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если в линейном пространстве определен базис, то
(1) его можно определить только одним способом
(2) вектора, входящие в базис линейно независимы
(3) любой вектор линейного пространства выражается через базис
(4) в некоторых случаях можно задать более
одного разложения вектора данного пространства по базису
Найти общее решение и одно частное решение системы уравнений
(1) общее решение
х1=(х3-3х4-2)/7
х2=(7х4+х3+3)/9
(2) общее решение
х3=(х1-9х2-2)/11
х4=(-5х1+х2+10)/11
(3) общее решение
х3=-11/8х4
х1=2/3х2+1/24х4-1/3
(4) частное решение
(-1/3,0,0,0)
(5) частное решение
(0,1/3,1,0)
(6) частное решение
(1,0,1/3,0) Найти производную от
det(A) по х, если
(1)
x2(x+3)(x-5)
(2)
x4-2x3-15x2
(3)
5x4+8x3-5x2
(4)
-5x4+8x3+5x2
(5)
x2(x-3)(x+5)
(6)
x4-2x3-15x2 Вектор ![math]() , удовлетворяющий соотношению
, удовлетворяющий соотношению ![math]() , называется:
, называется:
 , удовлетворяющий соотношению
, удовлетворяющий соотношению  , называется:
, называется:
(1) каноническим вектором
(2) собственным вектором
(3) собственным значением
Чему будет равен ранг матрицы
(1) 1
(2) 2
(3) 5
Какой будет угол между вектором ![math]() и линейным подпространством натянутым на векторы
и линейным подпространством натянутым на векторы ![math]()
 и линейным подпространством натянутым на векторы
и линейным подпространством натянутым на векторы 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие собственные значения будет иметь матрица
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая квадратичная форма, из ниже перечисленных, будет иметь вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие из матриц соответствуют паре прямая матрица - транспонированная матрица
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать верные утверждения
(1) существует матрица 3х3, у которой любые две
строки линейно независимы, а три зависимы
(2) кратности собственных чисел матриц
А и AT одинаковы
(3) собственные вектора матриц
А и A-1 различны Из равенства ![math]() следует, что
следует, что ![math]() , где k - степень
, где k - степень ![math]() . Приведенное выше доказательство, доказывает, что:
. Приведенное выше доказательство, доказывает, что:
 следует, что
следует, что  , где k - степень
, где k - степень  . Приведенное выше доказательство, доказывает, что:
. Приведенное выше доказательство, доказывает, что:
(1) если оператор ![math]() имеет собственное значение
имеет собственное значение ![math]() , то одно из чисел
, то одно из чисел ![math]() и
и ![math]() является собственным значением оператора
является собственным значением оператора ![math]()
 имеет собственное значение
имеет собственное значение  , то одно из чисел
, то одно из чисел  и
и  является собственным значением оператора
является собственным значением оператора 
(2) в пространстве ![math]() линейный оператор
линейный оператор ![math]() имеет множество собственных значений
имеет множество собственных значений ![math]()
 линейный оператор
линейный оператор  имеет множество собственных значений
имеет множество собственных значений 
(3) если оператор А невырожденный, то операторы А и ![math]() имеют одни и те же собственные векторы
имеют одни и те же собственные векторы
 имеют одни и те же собственные векторы
имеют одни и те же собственные векторы Какая система линейных уравнений, из ниже перечисленных, не имеет решений?
(1)
(2)
(3)
Линейное преобразование ![math]() в базисе
в базисе ![math]() имеет матрицу Как будет выглядеть матрица в базисе ?
имеет матрицу Как будет выглядеть матрица в базисе ?
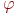 в базисе
в базисе  имеет матрицу Как будет выглядеть матрица в базисе ?
имеет матрицу Как будет выглядеть матрица в базисе ?
(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Какой канонический вид будут иметь уравнения поверхностей второго порядка ![math]() ?
?
 ?
?
(1)
(2)
(3)
Примерами линейного пространства являются
(1) множество столбцов
(2) множество строк
(3) множество ненулевых столбцов
(4) множество ненулевых строк
(5) все многочлены
(6) многочлены степени от n до m
Выбрать верные утверждения
(1) пусть характеристическое уравнение
(-1)
n n+...+det(A)=0, имеет только вещественные
корни, то их количество равно n с учетом кратности
(2) алгебраическая и геометрическая кратности корней соппадают
(3) для матриц размера
nxn ∃∈R:
det(A-(1-AT)=0 при n-нечетном Многочлены называются:
(1) инвариантными множителями ![math]() - матрицы
- матрицы ![math]()
 - матрицы
- матрицы 
(2) рангом ![math]() - матрицы
- матрицы
 - матрицы
- матрицы
(3) характеристическим многочленом матрицы А
Какое доказательство, из ниже перечисленных, доказывает теорему:"Для любого вектора ![math]() существует единственная ортогональная проекция на подпространство W"?
существует единственная ортогональная проекция на подпространство W"?
 существует единственная ортогональная проекция на подпространство W"?
существует единственная ортогональная проекция на подпространство W"?
(1) если ![math]() , то
, то ![math]() .
. ![math]() состоит из векторов
состоит из векторов ![math]() , т.е.
, т.е. ![math]() . Аналогично
. Аналогично ![math]() .
.
 , то
, то  .
.  состоит из векторов
состоит из векторов  , т.е.
, т.е.  . Аналогично
. Аналогично  .
.
(2) любой вектор ![math]() можно представить в виде
можно представить в виде ![math]() , где
, где ![math]() и
и ![math]() . Кроме того, если
. Кроме того, если ![math]() , то
, то ![math]() . В самом деле, тогда
. В самом деле, тогда ![math]() и
и ![math]() , поэтому
, поэтому ![math]() . Следовательно,
. Следовательно, ![math]() . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
 можно представить в виде
можно представить в виде  , где
, где  и
и  . Кроме того, если
. Кроме того, если  , то
, то  . В самом деле, тогда
. В самом деле, тогда  и
и  , поэтому
, поэтому  . Следовательно,
. Следовательно,  . Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
. Выберем в качестве базиса V объединение базисов Im P и Ker P. Вэтом базисе матрица оператора P имеет требуемый вид.
(3) Выберем в пространстве W ортонормированный базис ![math]() . Рассмотрим вектор
. Рассмотрим вектор ![math]() . Условие
. Условие ![math]() означает, что , т.е.
означает, что , т.е. ![math]() . Выбрав такие числа
. Выбрав такие числа ![math]() , получим требуемый вектор
, получим требуемый вектор ![math]() .
.
 . Рассмотрим вектор
. Рассмотрим вектор  . Условие
. Условие  означает, что , т.е.
означает, что , т.е.  . Выбрав такие числа
. Выбрав такие числа  , получим требуемый вектор
, получим требуемый вектор  .
. Если для любых элементов x и y ![math]() , то билинейная форма называется:
, то билинейная форма называется:
 , то билинейная форма называется:
, то билинейная форма называется:
(1) кимплектической
(2) кососимметрической
(3) симметрической
Как называется оператор ![math]() , если ?
, если ?
 , если ?
, если ?
(1) самосопряженным
(2) сопряженным линейному оператору ![math]()

(3) ортогональным
Какую матрицу имеет квадратичная форма ![math]() ?
?
 ?
?
(1)
(2)
(3)
Какая из матриц является единичной?
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать однородные системы линейных уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Найти
det A, если
(1) 4
(2) 5
(3) 6
(4) -4
(5) -5
(6) -6
Ранг матрицы будет равен:
(1) 5
(2) 3
(3) 6
Какие операторы являются линейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Выберите не верные утверждения:
(1) элементы x и y модуля с билинейной формой ![math]() называется ортогональной, если
называется ортогональной, если ![math]()
 называется ортогональной, если
называется ортогональной, если 
(2) если для любых элементов x и y ![math]() , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
 , то билинейная форма называется симметрической
, то билинейная форма называется симметрической
(3) если для каждого элемента x ![math]() , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической
 , то билинейная форма называется кососимметрической
, то билинейная форма называется кососимметрической Если матрицу транспонировать, то получится матрица ![math]() равная:
равная:
 равная:
равная:
(1)
(2)
(3)
Какое будет ортогональное преобразование неизвестных для квадратичной формы ![math]() , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
 , приводящую эту форму к каноническому виду?
, приводящую эту форму к каноническому виду?
(1)
(2)
(3)
Какие из утверждений верные?
(1) сложение матриц обладает свойством коммутативности
(2) сложение матриц обладает свойством дистрибутивности относительно умножения
(3) сложение матриц А + B определено только в том случае,
если матрица А имеет размерность mxn, а В nxm
Среди предложенных матриц выбрать те, у которых ранг равен 3
(1)
(2)
(3)
(4)
(5)
(6)
Какие из матриц являются минорами матрицы
(1)
(2)
(3)
(4)
(5)
(6)
Какие матрицы, из ниже перечисленных, не имеют ранг = 1?
(1)
(2)
(3)
Какие операторы являются нелинейными?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какое скалярное произведение будет иметь произвольные векторы ![math]() и
и ![math]() , при
, при ![math]() и
и ![math]() , при ?
, при ?
 и
и  , при
, при  и
и  , при ?
, при ?
(1) -1
(2) 4
(3) 0
Какая матрица, из ниже перечисленных, будет сопряженной матрицей, матрице
(1)
(2)
(3)
Какой индекс инерции будет иметь квадратичная форма ![math]() ?
?
 ?
?
(1) форма положительно определена
(2) каждый индекс инерции равен 2
(3) положительный индекс инерции равен 1, отрицательный индекс инерции равен 3
Какие из утверждений верные?
(1) умножение матриц обладает свойством ассоциативности
(2) умножение матриц обладает свойством коммутативности
(3) умножение и сложение матриц обладает свойством дистрибутивности
Дана система векторов. Какие из векторов входят в линейную оболочку указанной системы?
(1)
![math]()

(2)
(3)
(4)
(5)
Выбрать алгебраические дополнения для
(1)
(2)
(3)
(4)
(5)
(6)
Какие, из следующих отображений в соответствующих векторных пространствах являются линейными операторами?
(1) ![math]()

(2)
(3) ![math]()

Оператор Будет оператором:
(1) поворота относительно оси OY на угол ![math]()

(2) проецирования на плоскость x+y=0
(3) отражения относительно плоскости y-z=0
Каким вектором можно дополнить систему векторов: до ортогонального базиса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите не верные утверждения:
(1) Квадратная матрица А называется симметрической, если ![math]()

(2) Квадратная матрица А называется несимметрической, если ![math]()

(3) Квадратная матрица А называется эрмитовой, если ![math]()

Как будет выглядеть квадратичная форма ![math]() , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?
 , если привести ее к нормальному виду треугольным преобразованием неизвестных?
, если привести ее к нормальному виду треугольным преобразованием неизвестных?
(1) ![math]()

(2) ![math]()

(3)
Сумма каких матриц равна ?
(1)
(2)
(3)
(4)
(5)
Сколько подпространств размерности 1 может содержаться в
Rn при различных n
(1) 0
(2) 1
(3) 2
(4) 3
(5) 4
(6) бесконечно много
Выбрать четные перестановки
(1) (2,1,3,4)
(2) (1,3,4,2)
(3) (1,3,4,2)
(4) (1,4,2,3)
(5) (3,2,4,1)
(6) (2,4,1,3)
Какую матрицу будет иметь оператор дифференцирования в пространстве ![math]() в базисе
в базисе ![math]() ?
?
 в базисе
в базисе  ?
?
(1)
(2)
(3)
Какое собственное значение будет иметь матрица порядка n.
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какое скалярное произведение будет иметь вектор ![math]() ?
?
 ?
?
(1) 9
(2) 0
(3) 3
Какое ядро отображения будет иметь матрица
(1) базис ядра: ![math]()

(2) базис ядра: ![math]()

(3) базис ядра: ![math]()

Какое треугольное разложение будет иметь матрица при формуле ![math]() ?
?
 ?
?
(1)
(2)
(3)
Чему равно произведение матриц
(1)
(2)
(3)
(4)
(5)
(6)
Для двух линейных подпространств
L1 и L2
заданы базисы. Выбрать удовлетворяющие условию dim ( L1 + L2 ) = 5
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать правильные утверждения
(1) линейная комбинация строк, добавленная к матрице, ее детерминанта не меняет
(2) если детерминант матрицы равен нулю, то в матрице есть нулевой столбец
(3) если детерминант матрицы равен нулю, то в матрице есть нулевая строка
(4) если в матрице есть нулевой столбец, то детерминант матрицы равен нулю
(5) если в матрице есть нулевая строка, то детерминант матрицы равен нулю
(6)
Матрицы и будет иметь оператор:
(1) поворота трехмерного пространства на угол ![math]() вокруг прямой, заданной в прямоугольной системе координат уравнениями
вокруг прямой, заданной в прямоугольной системе координат уравнениями ![math]() , в базисе из единичных векторов осей координат
, в базисе из единичных векторов осей координат
 вокруг прямой, заданной в прямоугольной системе координат уравнениями
вокруг прямой, заданной в прямоугольной системе координат уравнениями  , в базисе из единичных векторов осей координат
, в базисе из единичных векторов осей координат
(2) ![math]() (А, В - фиксированные матрицы в пространстве
(А, В - фиксированные матрицы в пространстве ![math]() ) в базисе из матричных единиц
) в базисе из матричных единиц
 (А, В - фиксированные матрицы в пространстве
(А, В - фиксированные матрицы в пространстве  ) в базисе из матричных единиц
) в базисе из матричных единиц
(3) дифференцирования в пространстве ![math]() в базисе
в базисе ![math]()
 в базисе
в базисе 
Выберите верные утверждения:
(1) определитель ортогональной матрицы равен ![math]()

(2) всякое ортогональное преобразование неизвестных является невырожденным
(3) не всякая матрица с определителем равным ![math]() , будет ортогональной
, будет ортогональной
 , будет ортогональной
, будет ортогональной Какой нормированный вектор ортогонален к векторам ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3)
Базис ядра: ![math]() будет иметь матрица:
будет иметь матрица:
 будет иметь матрица:
будет иметь матрица:
(1)
(2)
(3)
Как будет выглядеть невырожденное линейное преобразование, которое приводит квадратичные формы к каноническому виду?
(1) матрицы форм F и G перестановочны . Ортогональное преобразование неизвестных приводит форму к каноническуому виду ![math]() , а форму G - к каноническому виду
, а форму G - к каноническому виду ![math]()
 , а форму G - к каноническому виду
, а форму G - к каноническому виду 
(2) форма F положительно определена. Преобразование неизвестных приводит форму F к нормальному виду, а форму G - к каноническому виду ![math]()

(3) форма F отрицательно определена. Преобразование неизвестных приводят форму F к нормальному виду, а форму G - к каноническому виду ![math]()

Какая из матриц является диагональной?
(1)
(2)
(3)
(4)
(5)
(6)
Выбрать наборы векторов, которые не могут составлять базис
(1)
(2)
(3)
(4)
(5)
(6)
(1) перстановка столбцов меняет знак детерминанта
(2) если
det(-A)=-det(A) и det(A)≠0, то матрица нечетной размерности
(3) если матрица нечетной размерности, то
det(-A)=-det(A) Пусть линейный оператор в пространстве ![math]() имеет в базисе матрицу Какая будет его матрица в базисе ?
имеет в базисе матрицу Какая будет его матрица в базисе ?
 имеет в базисе матрицу Какая будет его матрица в базисе ?
имеет в базисе матрицу Какая будет его матрица в базисе ?
(1)
(2)
(3)
Какое доказательство, из ниже переичсленных, доказывает, что, евклидово пространство, в котором определен нормальный оператор А,раскладывается в прямую ортогональную сумму инвариантных одномерных и двумерных неприводимых подпространств?
(1) пусть ![math]() . Тогда
. Тогда ![math]() и . Следовательно,
и . Следовательно, ![math]() .
.
 . Тогда
. Тогда  и . Следовательно,
и . Следовательно,  .
.
(2) инвариантное подпространство для нормального оператора инвариантно и для сопряженного и ограничение нормального оператора на инвариантном подпространстве нормально. Поэтому, пространство можно разбивать в прямую ортогональную сумму инвариантных подпространств до тех пор, пока не придем к одномерным подпространствам.
(3) для любой нормальной матрицы А существует унитарная матрица С такая, что ![math]() диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
 диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов.
диагональна. Именно, в качестве С можно взять матрицу преобразования от исходного базиса к ортонормированному базису из собственных векторов. Какая будет ортогональная проекция и перпендикуляр, опущенный из вектора x на подпространство L, при условиях, что ![math]() , L - задано системой уравнений:
, L - задано системой уравнений:
 , L - задано системой уравнений:
, L - задано системой уравнений:
(1) ![math]()

(2) ![math]()

(3) ![math]()

В пространстве многочленов ![math]() задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора ![math]() в базисе
в базисе ![math]()
 задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
задано скалярное произведение . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора  в базисе
в базисе 
(1)
(2)
(3)
Какие квадратные формы, из ниже перечисленных, будут иметь перестановочные формы матрицы?
(1)
(2)
(3) ![math]()

Какие из приведенных коэффициентов доказывают линейную зависимость (независимость) векторов
(1) 2, -1, 2, 2, 0
(2) 2, 1, 1, 0, -1
(3) 1, 2, -2, 1, 0
(4) 1, 1/2, 1/2, 0, -1/2
(5) 1/2, 1, -1/2, 0, 1
(6) 1, -1/2, 1, 0, -1/2
Определить, является ли линейным заданное подпространство для указанного пространства?
(1) Линейное пространство определено как всевозможные системы
действительных чисел
х=(х1,х2,х3). Сложение и умножение на число определены как
x+y=(x1+y1,x2+y2,x3+y3) ax=(ax1,ax2,ax3). Подпространство определено как
z=(z1,0,z3)
(2) Линейное пространство определено как всевозможные многочлены не выше пятой степени.
Подпространство - многочлены вида
a0t4+a1t2+a3
(3) Линейное пространство определено, как множество
геометрических векторов на плоскости. Подпространство - множество векторов с началом в начале
координат и лежащих в первой четверти
Найти собственные числа матрицы
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5
(6) 6
Какие подпространства, из перечисленных ниже, не являются инвариантными подпространствами для оператора дифференцирования в пространстве ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Доказательство, какой теоремы приведено ниже: Пусть ![math]() и
и ![math]() . По определению
. По определению ![math]() , поэтому
, поэтому
 и
и  . По определению
. По определению  , поэтому
, поэтому
(1) если ![math]() - ортонормированный базис пространства V и
- ортонормированный базис пространства V и ![math]() , то
, то ![math]()
 - ортонормированный базис пространства V и
- ортонормированный базис пространства V и  , то
, то 
(2) если w и ![math]() - ортогональные проекции вектора
- ортогональные проекции вектора ![math]() на подпространства W и
на подпространства W и ![math]() , то
, то ![math]()
 - ортогональные проекции вектора
- ортогональные проекции вектора  на подпространства W и
на подпространства W и  , то
, то 
(3) если ![math]() - ортогональная проекция вектора
- ортогональная проекция вектора ![math]() на подпространство W и
на подпространство W и ![math]() , то
, то
 - ортогональная проекция вектора
- ортогональная проекция вектора  на подпространство W и
на подпространство W и  , то
, то Какой биортогональный базис будет иметь базис пространства ![math]() :
:
 :
:
(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Вырожденной квадратичной формой называется:
(1) невырожденная матрица ![math]()

(2) вырожденная матрица ![math]()

(3) симметричная матрица ![math]() , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы
 , составленная из коэффициентов квадратичной формы
, составленная из коэффициентов квадратичной формы Вычислить значение
2C-3АВ, если
(1)
(2)
(3)
(4)
(5)
(6) В данном случае произвести расчет нельзя,
матрицы не согласованы по числу строк и столбцов
Линейное пространство определено как всевозможные системы
действительных чисел
х=(х1,х2,х3). Сложение и умножение на число определены как
x+y=(x1+y1,x2+y2,x3+y3) ax=(ax1,ax2,ax3). R1 - множество элементов вида
z=(0,0,z2) R2 - множество элементов вида z=(z1,0,0)
Найти R3=R1∩R2 и R4=R1+R2
(1)
R3 - множество элементов вида z=(0,0,z1)
(2)
R3 - множество элементов вида z=(z2,0,0)
(3)
R3 - пустое
(4)
R3=(0,0,0)
(5)
R4 - все пространство
(6)
R4- множество элементов вида z=(z2,0,z1) Какие из векторов являются собственными для характеристического
числа
=4 матрицы
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определите, какие подпространства в ![math]() и
и ![math]() , инвариантные относительно оператора
, инвариантные относительно оператора ![math]() :
:
 и
и  , инвариантные относительно оператора
, инвариантные относительно оператора  :
:
(1) ![math]()

(2) линейная оболочка любого множества одночленов степени не выше ![math]()

(3)
(4)
Как будет выглядеть матрица X в уравнении
(1)
(2)
(3)
Какой угол будет между векторами ![math]() ,
, ![math]() ?
?
 ,
,  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Квадратный корень будет иметь матрица:
(1)
(2)
(3)
Определить ![math]() , если
, если
 , если
, если
(1) 0
(2) 1
(3) 2
(4) 3
(5) 4
Найти базис
B и размерность подпространства L решений линейной однородной системы уравнений
(1)
(2)
(3)
(4)
(5)
(6)
Пусть
А - матрица 2х2 имеет два различных
собственных числа и А2=-А, то эти числа равны
(1) -2
(2) -1
(3) 0
(4) 1
(5) 2
Какие имеет собственные векторы и значения оператор ![math]() в пространстве
в пространстве ![math]()
 в пространстве
в пространстве 
(1) ![math]()

(2) одночлены
(3) ![math]()

Какая матрица, является обратной матрице где ![math]()

(1)
(2)
(3)
Какие будут длины сторон и внутренние углы треугольников, вершины которых заданы своими координатами ![math]() ?
?
 ?
?
(1) ![math]()
![math]()


(2) ![math]()
![math]()


(3) ![math]()
![math]()


При возведении матрицы в степень 3, получиться матрица:
(1)
(2)
(3)
Какое уравнение поверхностей 2-го порядка будет иметь канонический вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти координаты вектора в базисе
(1) 0,5 0,5 0,5
(2) 1,5 0,5 0,5
(3) 0,5 1,5 0,5
(4) 0,5 0,5 1,5
(5) 1,5 1,5 0,5
(6) 1,5 0,5 1,5
Найти общее решение и одно частное решение системы уравнений
(1) общее решение
х3=-4х1-3х2+1
х4=1
(2) общее решение
х3=(х1-9х2-2)/11
х4=(-5х1+х2+10)/11
(3) общее решение
х3=-11/8х4
х1=2/3х2+1/24х4-1/3
(4) частное решение
(-1,0,1,0)
(5) частное решение
(1,-1,0,1)
(6) частное решение
(1,0,1,0) Найти производную от
det(A) по х, если
(1)
x5-2x2
(2)
6x2(x3-1)
(3)
x3(x2-2)
(4)
6x2(x3+1)
(5)
6x5+6x2
(6)
6x5-6x2 Подпространство ![math]() линейного пространства
линейного пространства ![math]() называется инвариантным относительно оператора
называется инвариантным относительно оператора ![math]() , действующего в пространстве
, действующего в пространстве ![math]() , если:
, если:
 линейного пространства
линейного пространства  называется инвариантным относительно оператора
называется инвариантным относительно оператора  , действующего в пространстве
, действующего в пространстве  , если:
, если:
(1) ![math]()

(2) ![math]()

(3) для любого ![math]()

Чему будет равен ранг матрицы
(1) 1
(2) 2
(3) 3
Какой будет угол между плоскостями ![math]() и
и ![math]() , где ?
, где ?
 и
и  , где ?
, где ?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие собственные значения будет иметь матрица
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая квадратичная форма, из ниже перечисленных, будет иметь вид
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выберите верные утверждения:
(1) для любой матрицы
А найдется такая матрица
I, что AI=A, IA=A, называемая единичной
(2) из линейно зависимой системы векторов всегда можно выбрать несколько линейно независимых
(3) существуют такие
А и B, что rank (AB)=rank (BA)
(4) всегда
rank A=rank (ATA)
(5) всегда
rank(αA)=rank A Найти общее решение в зависимости от параметра
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выбрать верные утверждения
(1) не существует матрицы подобной самой себе
(2) собственные вектора матриц
А и A-1 одинаковы
(3) если
A такая, что A2+2A+I=0 то A-невырожденная Если ![math]() , то
, то ![math]() Приведенное выше доказательство, доказывает, что:
Приведенное выше доказательство, доказывает, что:
 , то
, то  Приведенное выше доказательство, доказывает, что:
Приведенное выше доказательство, доказывает, что:
(1) если оператор ![math]() имеет собственное значение
имеет собственное значение ![math]() , то одно из чисел
, то одно из чисел ![math]() и
и ![math]() является собственным значением оператора А
является собственным значением оператора А
 имеет собственное значение
имеет собственное значение  , то одно из чисел
, то одно из чисел  и
и  является собственным значением оператора А
является собственным значением оператора А
(2) в пространстве ![math]() линейный оператор
линейный оператор ![math]() имеет множество собственных значений
имеет множество собственных значений ![math]()
 линейный оператор
линейный оператор  имеет множество собственных значений
имеет множество собственных значений 
(3) если оператор ![math]() невырожденный, то операторы
невырожденный, то операторы ![math]() и
и ![math]() имеют одни и те же собственные векторы
имеют одни и те же собственные векторы
 невырожденный, то операторы
невырожденный, то операторы  и
и  имеют одни и те же собственные векторы
имеют одни и те же собственные векторы Какая система линейных уравнений, из ниже перечисленных, не имеет решений?
(1)
(2)
(3)
Линейное преобразование ![math]() в базисе
в базисе ![math]() имеет матрицу Как будет выглядеть матрица в базисе
имеет матрицу Как будет выглядеть матрица в базисе ![math]() ?
?
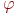 в базисе
в базисе  имеет матрицу Как будет выглядеть матрица в базисе
имеет матрицу Как будет выглядеть матрица в базисе  ?
?
(1)
(2)
(3)
Какой квадратный корень будет иметь матрица
(1)
(2)
(3)
Какой канонический вид будут иметь уравнения поверхностей второго порядка ![math]() ?
?
 ?
?
(1)
(2)
(3)
Примерами линейного пространства являются
(1) все непрерывные на отрезке функции
(2) все разрывные на отрезке функции
(3) все постоянные на отрезке функции
(4) множество иррациональных чисел
(5) множество положительных чисел
Выбрать варианты, при которых
det(A)=det(A).
(1) размерность матрицы равна 1
(2) матрица вырожденная
(3) матрица диагональная
(4) матрица единичная
(5)
=0 Матрица ![math]() называется:
называется:
 называется:
называется:
(1) характеристической для ![math]()

(2) собственным вектором матрицы ![math]()

(3) собственным значением матрицы ![math]()
