Главная /
Математика /
Математический анализ
Математический анализ - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе рассматриваются основные понятия математического анализа. Теоретический материал проиллюстрирован множеством примеров.
Все ответы: В курсе рассматриваются основные понятия математического анализа. Теоретический материал проиллюстрирован множеством примеров.
Пусть ![math]()
непрерывная функция и ![math]()
компактное множество. Тогда множество значений ![math]()
непрерывная функция и 
компактное множество. Тогда множество значений 
(1) компактное множество
(2) замкнутое, но не ограниченное
(3) ограниченное, но не замкнутое
(4) замкнутое и ограниченное
(5) может быть не ограниченным
(6) может быть не замкнутым
Каким условиям должна удовлетворять функция ![math]()
в теореме Ролля:
в теореме Ролля:
(1) непрерывность на ![math]()
(2) непрерывность на ![math]()
(3) дифференцируемость на ![math]()
(4) дифференцируемость в точке ![math]()
(5) ![math]()
(6) ![math]()
Поверхностью уровня функции ![math]()
являются
являются
(1) концентрические сферы с центром в точке ![math]()
(2) концентрические сферы с центром в любой точке
(3) концентрические сферы с центром в точке ![math]()
(4) ![math]()
Последовательность ![math]()
называется функциональной, если
называется функциональной, если
(1) ![math]()
функция и область определения ![math]()
функция и область определения 
(2) ![math]()
функция и область определения ![math]()
функция и область определения
(3) ![math]()
функция и область определения ![math]()
функция и область определения 
(4) ![math]()
функция и область определения ![math]()
функция и область определения Какие утверждения верны:
(1) каждый степенной ряд является функциональным
(2) каждый функциональный ряд является степенным
(3) каждый степенной ряд имеет ненулевой интервал сходимости
(4) интервал сходимости степенного ряда может равняться одной точке
(5) интервал сходимости степенного ряда может равняться числовой прямой
Если ![math]()
, то
, то
(1) ![math]()
- элемент множества ![math]()
- элемент множества 
(2) ![math]()
не является элементом множества ![math]()
не является элементом множества
(3) ![math]()
является подмножеством множества ![math]()
является подмножеством множества
(4) ![math]()
Расстояние между точками ![math]()
вычисляется по формуле
вычисляется по формуле
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Последовательность ![math]()
точек в ![math]()
- это отображение
точек в 
- это отображение
(1) ![math]()
(2) ![math]()
(3) ![math]()
Последовательность ![math]()
в пространстве ![math]()
называется фундаментальной, если
в пространстве называется фундаментальной, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функция ![math]()
называется равномерно непрерывной на множестве ![math]()
, если
называется равномерно непрерывной на множестве 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
В условиях теоремы Лагранжа точка с: ![math]()
(1) совпадает с концами отрезка ![math]()
или ![math]()
или 
(2) лежит вне отрезка ![math]()
(3) принадлежит интервалу ![math]()
(4) единственная
(5) хотя бы одна
Пусть функция ![math]()
задана на множестве ![math]()
. Тогда
задана на множестве 
. Тогда
(1) наибольшее значение функции на множестве ![math]()
достигается только в одной точке
достигается только в одной точке
(2) наибольшее значение функции на множестве ![math]()
достигается более чем в одной точке
достигается более чем в одной точке
(3) наибольшее значение функции на множестве ![math]()
достигается в точке ![math]()
достигается в точке 
(4) наибольшее значение функции на множестве ![math]()
достигается в точках ![math]()
достигается в точках 
Найти множество сходимости последовательности ![math]()
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- интервал сходимости степенного ряда ![math]()
. Тогда
- интервал сходимости степенного ряда 
. Тогда
(1) ряд расходится в точке ![math]()
(2) если ![math]()
, то ряд расходится
, то ряд расходится
(3) если ![math]()
, то ряд сходится
, то ряд сходится Какая операция отображена на рисунке?![files]()
(1) разность множеств
(2) сумма множеств
(3) пересечение множеств
(4) симметрическая разность
Множество ![math]()
называется
называется
(1) открытым шаром радиуса ![math]()
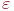
(2) замкнутым шаром радиуса ![math]()
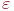
(3) открытым параллелепипедом
(4) замкнутым параллелепипедом
Пусть числовая последовательность ![math]()
. Тогда она
. Тогда она
(1) невозрастающая
(2) неубывающая
(3) ограниченная
(4) немонотонная
Последовательность ![math]()
в пространстве ![math]()
фундаментальная. Какие утверждения верны:
в пространстве фундаментальная. Какие утверждения верны:
(1) ![math]()
расходится
расходится
(2) ![math]()
ограниченная
ограниченная
(3) существует сходящаяся подпоследовательность ![math]()
(4) ![math]()
невозрастающая
невозрастающая Пусть ![math]()
. Для каких множеств ![math]()
справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
. Для каких множеств справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
(1) ![math]()
- замкнутое множество
- замкнутое множество
(2) ![math]()
- компактное множество
- компактное множество
(3) ![math]()
- ограниченное множество
- ограниченное множество Какое условие теоремы Ролля не выполняется для функции ![math]()
:
:
(1) непрерывность на ![math]()
(2) дифференцируемость на ![math]()
(3) f(a)=f(b)
Пусть для функции ![math]()
в точке ![math]()
существует градиент ![math]()
. Тогда
в точке 
существует градиент 
. Тогда
(1) ![math]()
в точке ![math]()
в точке
(2) градиент перпендикулярен к линии уровня ![math]()
(3) градиент направлен по касательной к линии уровня ![math]()
(4) ![math]()
(5) ![math]()
Последовательность ![math]()
сходится к ![math]()
равномерно на множестве ![math]()
, если
сходится к равномерно на множестве 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какие утверждения верны:
(1) если степенной ряд сходится в точке ![math]()
, то она лежит в интервале сходимости
, то она лежит в интервале сходимости
(2) если точка ![math]()
лежит в интервале сходимости, то степенной ряд сходится в этой точке
лежит в интервале сходимости, то степенной ряд сходится в этой точке
(3) если степенной ряд расходится в точке ![math]()
, то она лежит в интервале сходимости
, то она лежит в интервале сходимости
(4) если точка ![math]()
не лежит в интервале сходимости, то степенной ряд расходится в этой точке
не лежит в интервале сходимости, то степенной ряд расходится в этой точке Сколько подмножеств имеется у множества, состоящего из четырех элементов?
(1) 16
(2) 8
(3) 4
(4) 10
Отметьте верные утверждения:
(1) последовательность вложенных открытых шаров в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(2) последовательность вложенных замкнутых шаров в ![math]()
имеет пустое пересечение
имеет пустое пересечение
(3) последовательность вложенных замкнутых шаров в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(4) последовательность вложенных открытых шаров в ![math]()
имеет пустое пересечение
имеет пустое пересечение
(5) в каждый открытый шар можно вписать замкнутый параллелепипед
Точка ![math]()
называется пределом последовательности ![math]()
,если
называется пределом последовательности 
,если
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется пределом функции ![math]()
при стремлениии ![math]()
, если
называется пределом функции при стремлениии 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Число ![math]()
называется левым пределом ![math]()
числовой функции ![math]()
, если
называется левым пределом 
числовой функции 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функция ![math]()
называется неубывающей на множестве ![math]()
, если ![math]()
называется неубывающей на множестве 
, если 
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) если ![math]()
в точке ![math]()
, то ![math]()
в точке ![math]()
в точке , то 
в точке
(2) если ![math]()
в точке ![math]()
, то ![math]()
в точке ![math]()
в точке , то в точке
(3) если ![math]()
непрерывны в точке ![math]()
, то ![math]()
непрерывны в точке , то 
(4) если ![math]()
в точке ![math]()
, то ![math]()
в точке , то Последовательность ![math]()
сходится равномерно к ![math]()
тогда и только тогда, когда
сходится равномерно к тогда и только тогда, когда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Радиус сходимости степенного ряда ![math]()
равен
равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
В каком отношении находятся множества ![math]()
и ![math]()
, если ![math]()
, ![math]()
и 
, если 
, 
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется внутренней точкой множества ![math]()
, если
называется внутренней точкой множества 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Число ![math]()
называется пределом числовой последовательности ![math]()
, если
называется пределом числовой последовательности 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
. Тогда ![math]()
. Тогда
(1) неограниченна
(2) ограничена в любой окрестности точки ![math]()
(3) ограничена в некоторой окрестности точки ![math]()
(4) ограничена в открытом множестве, содержащем ![math]()
Пусть числовая функция ![math]()
- непрерывна в точке ![math]()
. Тогда
- непрерывна в точке . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
непрерывна на ![math]()
и дифференцируема на ![math]()
. Какое утверждение верно:
непрерывна на и дифференцируема на . Какое утверждение верно:
(1) если ![math]()
на ![math]()
, то ![math]()
возрастает на ![math]()
на , то возрастает на
(2) если ![math]()
возрастает на ![math]()
, то ![math]()
на ![math]()
возрастает на , то 
на
(3) если ![math]()
возрастает на ![math]()
, то ![math]()
на ![math]()
возрастает на , то на
(4) если ![math]()
, то ![math]()
локально возрастает
, то локально возрастает
(5) если ![math]()
, то ![math]()
локально возрастает
, то локально возрастает Пусть задана функция ![math]()
. На каких множествах существует неявная функция ![math]()
:
. На каких множествах существует неявная функция 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Последовательность ![math]()
сходится равномерно на множестве
сходится равномерно на множестве
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Сумма степенного ряда
(1) может быть разрывной функцией на интервале сходимости
(2) является разрывной функцией на интервале сходимости
(3) непрерывна на интервале сходимости
(4) может быть непрерывной или разрывной функцией на интервале сходимости
Чему равно множество ![math]()
, если ![math]()
, ![math]()
, если 
, 
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
- внутренняя точка множества ![math]()
. Тогда ![math]()
- внутренняя точка множества . Тогда 
(1) принадлежит множеству ![math]()
(2) принадлежит множеству ![math]()
(3) граничная точка множества ![math]()
(4) граничная точка множества ![math]()
(5) предельная точка множества ![math]()
(6) предельная точка множества ![math]()
Пусть ![math]()
. Тогда последовательность ![math]()
. Тогда последовательность
(1) монотонная
(2) ограниченная
(3) все точки последовательности лежат в некотором шаре
(4) возрастает или убывает
Пусть ![math]()
. ![math]()
и ![math]()
. Тогда функция ![math]()
имеет предел и он равен
. 
и 
. Тогда функция 
имеет предел и он равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка для функции ![math]()
является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть задана функция ![math]()
. Тогда
. Тогда
(1) ![math]()
убывает на ![math]()
убывает на 
(2) ![math]()
убывает на ![math]()
убывает на 
(3) ![math]()
непрерывна на ![math]()
непрерывна на
(4) ![math]()
(5) ![math]()
Пусть ![math]()
непрерывна в окрестности точки ![math]()
и ![math]()
непрерывные в окрестности ![math]()
. Какие условия достаточны для существования единственной неявной функции ![math]()
:
непрерывна в окрестности точки 
и 
непрерывные в окрестности . Какие условия достаточны для существования единственной неявной функции 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть последовательность ![math]()
равномерно сходится к ![math]()
на множестве ![math]()
. Какие утверждения верны:
равномерно сходится к на множестве 
. Какие утверждения верны:
(1) последовательность разрывных на ![math]()
функций ![math]()
может сходиться к непрерывной ![math]()
функций 
может сходиться к непрерывной
(2) последовательность ограниченных на ![math]()
функций ![math]()
сходится к неограниченной ![math]()
функций сходится к неограниченной
(3) если ![math]()
разрывны на ![math]()
, то ![math]()
разрывна на ![math]()
разрывны на , то разрывна на
(4) если ![math]()
непрерывны на ![math]()
, то ![math]()
непрерывна на ![math]()
непрерывны на , то непрерывна на Пусть задан ряд ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) интервал сходимости ряда – вся числовая прямая
(2) интервал сходимости ряда – множество ![math]()
(3) на концах интервала сходимости ряд сходится
(4) ряд сходится равномерно на ![math]()
(5) сумма ряда непрерывна на ![math]()
Множество ![math]()
состоит из трех элементов, а множество ![math]()
- из двух элементов. Сколько существует отображений M на P?
состоит из трех элементов, а множество 
- из двух элементов. Сколько существует отображений M на P?
(1) 6
(2) 1
(3) 8
(4) 4
Множеством ![math]()
всех внутренних точек открытого шара
всех внутренних точек открытого шара
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
сходящаяся. Тогда предел последовательности
сходящаяся. Тогда предел последовательности
(1) может быть предельной точкой множества значений последовательности ![math]()
(2) может не быть предельной точкой множества значений последовательности ![math]()
(3) может быть изолированной точкой множества значений последовательности ![math]()
(4) есть предельная точка ![math]()
, если оно конечно
, если оно конечно
(5) есть предельная точка ![math]()
, если оно бесконечно
, если оно бесконечно Функция ![math]()
называется непрерывной в точке ![math]()
, если
называется непрерывной в точке 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Предел ![math]()
существует и равен
существует и равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
непрерывна на ![math]()
и дифференцируема на ![math]()
. Какие утверждения верны:
непрерывна на 
и дифференцируема на 
. Какие утверждения верны:
(1) если ![math]()
не ограниченна на ![math]()
, то ![math]()
равномерно непрерывна на ![math]()
не ограниченна на , то равномерно непрерывна на
(2) если ![math]()
ограниченна на ![math]()
, то ![math]()
равномерно непрерывна на ![math]()
ограниченна на , то равномерно непрерывна на
(3) если ![math]()
равномерно непрерывна на ![math]()
, то ![math]()
ограниченна на ![math]()
равномерно непрерывна на , то ограниченна на
(4) если ![math]()
не равномерно непрерывна на ![math]()
, то ![math]()
не ограниченна на ![math]()
не равномерно непрерывна на , то не ограниченна на Уравнение ![math]()
не определяет неявной функции в достаточно малой окрестности точки ![math]()
. Какое условие не выполнено:
не определяет неявной функции в достаточно малой окрестности точки 
. Какое условие не выполнено:
(1) ![math]()
непрерывна в окрестности точки ![math]()
непрерывна в окрестности точки
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функциональным рядом для последовательности ![math]()
называется выражение
называется выражение
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какое уравнения является обыкновенным дифференциальным уравнением 1-го порядка?
(1) ![math]()
(2) ![math]()
(3) ![math]()
Запишите бесконечную периодическую десятичную дробь ![math]()
в виде ![math]()
, если ![math]()
и ![math]()
- натуральные числа, не имеющие общих делителей.
в виде 
, если 
и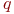 
- натуральные числа, не имеющие общих делителей.
(1) 211/99
(2) 353/495
(3) 2/13
(4) 13/2
Множество ![math]()
называется открытым, если
называется открытым, если
(1) некоторые его точки внутренние
(2) любая его точка внутренняя
(3) любая точка из его дополнения ![math]()
внутренняя
внутренняя
(4) некоторые точки из его дополнения ![math]()
внутренние
внутренние Число ![math]()
называется частичным пределом последовательности ![math]()
, если
называется частичным пределом последовательности , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть функции ![math]()
. Какие условия достаточны для того, чтобы функция ![math]()
была непрерывной в точке ![math]()
:
. Какие условия достаточны для того, чтобы функция была непрерывной в точке 
:
(1) ![math]()
непрерывна в ![math]()
и ![math]()
непрерывна в ![math]()
непрерывна в и 
непрерывна в
(2) ![math]()
непрерывна в ![math]()
или ![math]()
непрерывна в ![math]()
непрерывна в или непрерывна в
(3) ![math]()
(4) ![math]()
Производной функции ![math]()
в данной точке ![math]()
называется
в данной точке называется
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какое выражение является многочленом Тейлора ![math]()
для ![math]()
раз дифференцируемой в окрестности точки ![math]()
функции ![math]()
для 
раз дифференцируемой в окрестности точки функции 
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
является точкой локального максимума для функции ![math]()
, если существует окрестность ![math]()
:
является точкой локального максимума для функции 
, если существует окрестность 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какое множество является областью сходимости ряда ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
- решение дифференциального уравнения ![math]()
. Тогда
- решение дифференциального уравнения 
. Тогда
(1) ![math]()
- дифференцируемая на ![math]()
функция
- дифференцируемая на 
функция
(2) ![math]()
(3) ![math]()
(4) область определения ![math]()
Сумма двух иррациональных чисел
(1) всегда рациональна
(2) всегда иррациональна
(3) может быть как рациональной, так и иррациональной
Пусть множество ![math]()
открыто. Какие утверждения верны:
открыто. Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
(7) ![math]()
Пусть в некоторой окрестности точки ![math]()
содержится конечное число элементов последовательности ![math]()
. Какие утверждения верны:
содержится конечное число элементов последовательности . Какие утверждения верны:
(1) ![math]()
ограниченная
ограниченная
(2) ![math]()
сходится к ![math]()
сходится к
(3) ![math]()
расходится
расходится
(4) все неверно
Пусть функции ![math]()
. Сложная функция ![math]()
непрерывна ![math]()
, если
. Сложная функция 
непрерывна , если
(1) ![math]()
непрерывна в ![math]()
и ![math]()
непрерывна в ![math]()
непрерывна в и непрерывна в 
(2) ![math]()
непрерывна в ![math]()
или ![math]()
непрерывна в ![math]()
непрерывна в или непрерывна в
(3) ![math]()
(4) ![math]()
(5) ![math]()
Пусть ![math]()
. Сколько точек пересечения касательной к графику функции в точке ![math]()
и графика функции в произвольной окрестности точки ![math]()
:
. Сколько точек пересечения касательной к графику функции в точке и графика функции в произвольной окрестности точки 
:
(1) одна
(2) конечное число
(3) бесконечное число
Множество ![math]()
называется выпуклым, если
называется выпуклым, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
точка экстремума дифференцируемой функции ![math]()
. Тогда
точка экстремума дифференцируемой функции . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какая функция является суммой ряда ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Что является общим решением дифференциального уравнения ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Найти нижнюю грань множества рациональных чисел ![math]()
, удовлетворяющих неравенству ![math]()
, удовлетворяющих неравенству 
(1) ![math]()
(2) ![math]()
(3) 0
(4) 4
- множество рациональных чисел. Какие утверждения верны:
(1) ![math]()
содержит хотя бы одну изолированную точку
содержит хотя бы одну изолированную точку
(2) любая его точка является граничной
(3) ![math]()
- замкнутое множество
- замкнутое множество
(4) ![math]()
не является открытым
не является открытым
(5) граница множества содержит множество ![math]()
иррациональных чисел
иррациональных чисел
(6) граница множества совпадает с множеством ![math]()
иррациональных чисел
иррациональных чисел Пусть числовые последовательности ![math]()
и ![math]()
сходятся и ![math]()
. Какие утверждения верны:
и 
сходятся и 
. Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
. Какие утверждения справедливы:
. Какие утверждения справедливы:
(1) если ![math]()
непрерывная, то ![math]()
ограниченная на ![math]()
, ![math]()
- компактное множество
непрерывная, то ограниченная на , - компактное множество
(2) если ![math]()
ограниченная, то ![math]()
непрерывная ![math]()
, ![math]()
- компактное множество
ограниченная, то непрерывная , - компактное множество
(3) если ![math]()
непрерывная, то ![math]()
ограниченная на ![math]()
, ![math]()
- замкнутое множество
непрерывная, то ограниченная на , - замкнутое множество
(4) если ![math]()
ограниченная, то ![math]()
непрерывная ![math]()
, ![math]()
- замкнутое множество
ограниченная, то непрерывная , - замкнутое множество Пусть функция ![math]()
обратима в окрестности точки ![math]()
и ![math]()
- обратная функция. Тогда производная ![math]()
в точке ![math]()
равна
обратима в окрестности точки и 
- обратная функция. Тогда производная 
в точке 
равна
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Чему равны частные производные ![math]()
функции ![math]()
:
функции 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
является точкой локального максимума для функции ![math]()
при условиях ![math]()
, если для ![math]()
существует окрестность ![math]()
:
является точкой локального максимума для функции 
при условиях 
, если для 
существует окрестность 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функциональный ряд ![math]()
сходится равномерно к функции ![math]()
на множестве ![math]()
тогда и только тогда, когда
сходится равномерно к функции 
на множестве 
тогда и только тогда, когда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4)
Какие условия входят в достаточные для существования и единственности решения задачи Коши ![math]()
:
:
(1) ![math]()
непрерывна в некоторой окрестности ![math]()
непрерывна в некоторой окрестности
(2) ![math]()
ограничена в некоторой окрестности ![math]()
ограничена в некоторой окрестности
(3) ![math]()
(4) ![math]()
Существуют ли действительные корни уравнения ![math]()
(1) существуют
(2) не существуют
Пусть ![math]()
. Какое множество является множеством предельных точек ![math]()
:
. Какое множество является множеством предельных точек 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовые последовательности ![math]()
и ![math]()
сходятся и ![math]()
.Тогда последовательность ![math]()
сходится и ее предел равен
и сходятся и 
.Тогда последовательность 
сходится и ее предел равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть задана функция ![math]()
. Какие утверждения справедливы:
. Какие утверждения справедливы:
(1) если ![math]()
непрерывная, то ![math]()
достигает своих верхней и нижней грани на ![math]()
, ![math]()
- компакт
непрерывная, то достигает своих верхней и нижней грани на , - компакт
(2) если ![math]()
непрерывная, то ![math]()
достигает своих верхней и нижней грани на ![math]()
, ![math]()
- замкнутое множество
непрерывная, то достигает своих верхней и нижней грани на , - замкнутое множество
(3) если ![math]()
непрерывная, то ![math]()
достигает своих верхней и нижней грани на ![math]()
, ![math]()
- ограниченное множество
непрерывная, то достигает своих верхней и нижней грани на , - ограниченное множество Точка ![math]()
является точкой локального минимума функции ![math]()
, если
является точкой локального минимума функции , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
.Какие утверждения верны:
.Какие утверждения верны:
(1) если ![math]()
в данной точке ![math]()
, то ![math]()
непрерывна в ![math]()
в данной точке 
, то 
непрерывна в
(2) если ![math]()
дифференцируема в ![math]()
, то она непрерывна в ![math]()
дифференцируема в , то она непрерывна в
(3) если ![math]()
дифференцируема в ![math]()
, то ![math]()
в точке ![math]()
дифференцируема в , то в точке
(4) если ![math]()
в точке ![math]()
, то ![math]()
дифференцируема в ![math]()
в точке , то дифференцируема в Пусть ![math]()
- точка условного экстремума функции ![math]()
и задана функция Лагранжа ![math]()
. Тогда
- точка условного экстремума функции 
и задана функция Лагранжа 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Какие условия достаточны для того, чтобы функциональный ряд ![math]()
сходился равномерно на множестве ![math]()
:
сходился равномерно на множестве :
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть у задачи Коши ![math]()
решение ![math]()
является продолжением решения ![math]()
. Тогда
решение 
является продолжением решения 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
К свойствам вещественных чисел относятся:
(1) свойство упорядоченности
(2) распределительный закон умножения
(3) свойство Архимеда
Пусть числовая последовательность ![math]()
сходится. Какие варианты возможны?
сходится. Какие варианты возможны?
(1) ![math]()
ограниченная сверху и неубывающая
ограниченная сверху и неубывающая
(2) ![math]()
ограниченная сверху и невозрастающая
ограниченная сверху и невозрастающая
(3) ![math]()
ограниченная снизу и неубывающая
ограниченная снизу и неубывающая
(4) ![math]()
ограниченная снизу и невозрастающая
ограниченная снизу и невозрастающая Пусть задана непрерывная числовая функция ![math]()
. Пусть ![math]()
. Тогда
. Пусть 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
- точка локального экстремума дифференцируемой функции ![math]()
. Тогда
- точка локального экстремума дифференцируемой функции . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) непрерывна на ![math]()
(2) ![math]()
(3) ![math]()
дифференцируема в ![math]()
дифференцируема в
(4) ![math]()
непрерывны в ![math]()
непрерывны в Пусть ![math]()
точка экстремума функции ![math]()
при условии ![math]()
. Тогда линия уровня ![math]()
пересекает кривую ![math]()
под углом
точка экстремума функции при условии 
. Тогда линия уровня 
пересекает кривую 
под углом
(1) ![math]()
(2) ![math]()
(3) ![math]()
Какой числовой ряд нужно использовать для доказательства равномерной сходимости ряда ![math]()
по признаку Вейерштрасса:
по признаку Вейерштрасса:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана задача Коши ![math]()
. Тогда
. Тогда
(1) уравнение является линейным
(2) ![math]()
имеет неограниченную производную в некоторой ограниченной по ![math]()
области
имеет неограниченную производную в некоторой ограниченной по 
области
(3) условие Липшица выполнено для произвольной ограниченной по ![math]()
области
области
(4) функция ![math]()
- решение задачи Коши
- решение задачи Коши
(5) решение ![math]()
можно продолжить для ![math]()
можно продолжить для 
При выполнении каких условий разбиение рациональных чисел A и B называется сечением?
(1) каждый из классов A и B не пуст
(2) множества A и B не пересекаются
(3) каждое рациональное число принадлежит одному из классов A и B
(4) множества A и B пересекаются
Пусть числовая последовательность ![math]()
ограничена. Тогда
ограничена. Тогда
(1) существует только одна сходящаяся подпоследовательность ![math]()
(2) существует хотя бы одна сходящаяся подпоследовательность ![math]()
(3) любая подпоследовательность ![math]()
сходится
сходится
(4) любая подпоследовательность ![math]()
расходится
расходится На каком множестве функция ![math]()
является непрерывной:
является непрерывной:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовая последовательность ![math]()
ограничена. ![math]()
- множество частичных пределов последовательности ![math]()
. Какие утверждения верны:
ограничена. - множество частичных пределов последовательности . Какие утверждения верны:
(1) ![math]()
- ограничено
- ограничено
(2) ![math]()
- неограниченное
- неограниченное
(3) ![math]()
- открытое
- открытое
(4) ![math]()
- замкнутое
- замкнутое Пусть задана функция ![math]()
. Тогда она
. Тогда она
(1) непрерывна на всей плоскости, кроме начала координат
(2) ограничена на оси ![math]()
(3) достигает свои точные грани на всей плоскости
(4) обращается в ноль на отрезке ![math]()
(5) неограниченна на множестве ![math]()
Пусть ![math]()
- сходящаяся к точке ![math]()
последовательность элементов замкнутого множества ![math]()
. Тогда
- сходящаяся к точке последовательность элементов замкнутого множества 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
может принадлежать или не принадлежать множеству ![math]()
может принадлежать или не принадлежать множеству Пусть ![math]()
, ![math]()
- множество частичных пределов ![math]()
. Какие утверждения верны:
, - множество частичных пределов . Какие утверждения верны:
(1) ![math]()
неубывающая
неубывающая
(2) ![math]()
ограничена сверху
ограничена сверху
(3) ![math]()
сходится
сходится
(4) ![math]()
(5) ![math]()
Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) ![math]()
неограниченная снизу
неограниченная снизу
(2) ![math]()
невозрастающая
невозрастающая
(3) ![math]()
сходится
сходится
(4) предел последовательности – предельная точка множества значений
Найдите предел последовательности ![math]()
, если ![math]()
. Выберете правильные ответ:
, если 
. Выберете правильные ответ:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
непрерывная функция. Какие утверждения верны:
непрерывная функция. Какие утверждения верны:
(1) если ![math]()
открытое множество, то и ![math]()
открытое множество
открытое множество, то и 
открытое множество
(2) если ![math]()
замкнутое множество, то и ![math]()
замкнутое множество
замкнутое множество, то и замкнутое множество
(3) если ![math]()
компактное множество, то и ![math]()
компактное множество
компактное множество, то и компактное множество Каким условиям должна удовлетворять функция ![math]()
в теореме Лагранжа:
в теореме Лагранжа:
(1) непрерывность на ![math]()
(2) непрерывность на ![math]()
(3) дифференцируемость на ![math]()
(4) дифференцируемость в точке ![math]()
(5) ![math]()
(6) ![math]()
Поверхностью уровня функции ![math]()
являются
являются
(1) ![math]()
(2) концентрические сферы радиусом ![math]()
с центром в точке ![math]()
с центром в точке
(3) концентрические сферы радиусом ![math]()
с центром в точке ![math]()
с центром в точке
(4) параболоиды вращения с вершиной в точке ![math]()
(5) параболоиды вращения с вершиной в точке ![math]()
Точка ![math]()
называется точкой сходимости функциональной последовательности ![math]()
, если
называется точкой сходимости функциональной последовательности , если
(1) числовая последовательность ![math]()
сходится
сходится
(2) числовая последовательность ![math]()
расходится
расходится
(3) ![math]()
(4) ![math]()
Какие утверждения верны:
(1) каждый степенной ряд является функциональным
(2) каждый функциональный ряд является степенным
(3) степенной ряд может иметь нулевой интервал сходимости
(4) интервал сходимости степенного ряда открытое множество
(5) интервал сходимости степенного ряда может равняться числовой прямой
Если ![math]()
, то
, то
(1) ![math]()
- элемент множества ![math]()
- элемент множества
(2) ![math]()
не является элементом множества ![math]()
не является элементом множества
(3) ![math]()
является подмножеством множества ![math]()
является подмножеством множества
(4) ![math]()
Расстояние ![math]()
в ![math]()
обладает свойствами:
в обладает свойствами:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Пусть задана последовательность ![math]()
. Какая последовательность натуральных чисел задает подпоследовательность ![math]()
:
. Какая последовательность натуральных чисел задает подпоследовательность 
:
(1) ![math]()
(2) ![math]()
Последовательность ![math]()
в пространстве ![math]()
называется нефундаментальной, если
в пространстве называется нефундаментальной, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
и ![math]()
. Тогда функция ![math]()
называется
и . Тогда функция называется
(1) непрерывной на множестве ![math]()
(2) равномерно непрерывной на множестве ![math]()
(3) непрерывной на множестве ![math]()
(4) равномерно непрерывной на множестве ![math]()
Геометрический смысл теоремы Ролля состоит в том, что существует хотя бы одна точка графика функции ![math]()
, в которой касательная
, в которой касательная
(1) параллельна оси ![math]()
(2) параллельна оси ![math]()
(3) перпендикулярна оси ![math]()
(4) перпендикулярна оси ![math]()
(5) параллельна хорде ![math]()
Пусть функция ![math]()
задана на множестве ![math]()
. Тогда
задана на множестве 
. Тогда
(1) наибольшее значение функции на множестве ![math]()
достигается только в одной точке
достигается только в одной точке
(2) наибольшее значение функции на множестве ![math]()
достигается более чем в одной точке
достигается более чем в одной точке
(3) наибольшее значение функции на множестве ![math]()
не достигается
не достигается
(4) наименьшее значение функции на множестве ![math]()
достигается только в одной точке
достигается только в одной точке
(5) наименьшее значение функции на множестве ![math]()
достигается более чем в одной точке
достигается более чем в одной точке
(6) наименьшее значение функции на множестве ![math]()
не достигается
не достигается Найти предел последовательности ![math]()
на множестве ![math]()
:
на множестве 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
- интервал сходимости степенного ряда ![math]()
. Тогда
- интервал сходимости степенного ряда . Тогда
(1) ряд сходится в точке ![math]()
(2) если ![math]()
, то ряд расходится
, то ряд расходится
(3) если ![math]()
, то ряд сходится
, то ряд сходится Какая операция отображена на рисунке?![files]()
(1) объединение множеств
(2) разность множеств
(3) пересечение множеств
(4) симметрическая разность
Множество ![math]()
называется
называется
(1) открытым шаром радиуса ![math]()
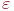
(2) замкнутым шаром радиуса ![math]()
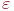
(3) открытым параллелепипедом
(4) замкнутым параллелепипедом
Пусть числовая последовательность ![math]()
. Тогда она
. Тогда она
(1) невозрастающая
(2) неубывающая
(3) ограниченная
(4) немонотонная
Последовательность ![math]()
в пространстве ![math]()
нефундаментальная. Какие утверждения верны:
в пространстве нефундаментальная. Какие утверждения верны:
(1) ![math]()
расходится
расходится
(2) ![math]()
ограниченная
ограниченная
(3) Существует сходящаяся подпоследовательность ![math]()
(4) Все неверно
Пусть ![math]()
. Для каких множеств ![math]()
справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
. Для каких множеств справедливо утверждение: из непрерывности на множестве функции следует ее равномерная непрерывность:
(1) ![math]()
- замкнутое множество
- замкнутое множество
(2) ![math]()
- компактное множество
- компактное множество
(3) ![math]()
- ограниченное множество
- ограниченное множество Какое условие теоремы Ролля не выполняется для функции ![math]()
, где ![math]()
- означает целую часть от числа:
, где 
- означает целую часть от числа:
(1) непрерывность на ![math]()
(2) дифференцируемость на ![math]()
(3) f(a)=f(b)
Пусть функция ![math]()
. Тогда ![math]()
равен
. Тогда равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Последовательность ![math]()
не сходится к ![math]()
равномерно на множестве ![math]()
, если
не сходится к равномерно на множестве , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно
- подмножество интервала сходимости. Тогда ряд сходится на множестве равномерно, если оно
(1) произвольное
(2) замкнутое
(3) ограниченное
(4) компактное
Сколько подмножеств имеется у множества, состоящего из ![math]()
элементов
элементов
(1) 1
(2) 2n
(3) n2
(4) 2n
Отметьте верные утверждения:
(1) последовательность вложенных открытых параллелепипедов в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(2) последовательность вложенных замкнутых параллелепипедов в ![math]()
имеет пустое пересечение
имеет пустое пересечение
(3) последовательность вложенных замкнутых параллелепипедов в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(4) последовательность вложенных открытых параллелепипедов в ![math]()
имеет пустое пересечение
имеет пустое пересечение
(5) в каждый замкнутый параллелепипед можно вписать открытый шар
Пусть ![math]()
. Тогда вне каждой окрестности ![math]()
-
. Тогда вне каждой окрестности 
-
(1) бесконечное, начиная с некоторого номера, число точек ![math]()
(2) конечное число точек ![math]()
(3) все точки ![math]()
Точка ![math]()
называется пределом функции ![math]()
при стремлениии ![math]()
, если
называется пределом функции при стремлениии , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Число ![math]()
называется правым пределом ![math]()
числовой функции ![math]()
, если
называется правым пределом 
числовой функции , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функция ![math]()
называется невозрастающей на ![math]()
, если ![math]()
называется невозрастающей на , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
. Тогда частные производные 2 порядка равны:
. Тогда частные производные 2 порядка равны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Последовательность ![math]()
сходится равномерно к ![math]()
на множестве ![math]()
. Тогда
сходится равномерно к на множестве . Тогда
(1) ![math]()
сходится к ![math]()
на ![math]()
сходится к на
(2) ![math]()
не сходится к ![math]()
на ![math]()
не сходится к на
(3) ![math]()
(4) ![math]()
Если ![math]()
, то интервал сходимости ряда ![math]()
, то интервал сходимости ряда
(1) равен числовой прямой
(2) равен интервалу ![math]()
(3) вырождается в одну точку ![math]()
В каком отношении находятся множества ![math]()
и ![math]()
, если ![math]()
, ![math]()
и , если 
, 
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется внешней точкой множества ![math]()
, если
называется внешней точкой множества , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Пусть числовая последовательность ![math]()
- множество частичных пределов ![math]()
. Верхний предел числовой последовательности ![math]()
- это
- множество частичных пределов . Верхний предел числовой последовательности 
- это
(1) верхняя грань множества ![math]()
, большая ![math]()
, большая 
(2) нижняя грань множества ![math]()
, меньшая ![math]()
, меньшая 
(3) ![math]()
(4) ![math]()
Пусть ![math]()
. Какие утверждения справедливы:
. Какие утверждения справедливы:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется точкой устранимого разрыва функции ![math]()
, если в точке ![math]()
называется точкой устранимого разрыва функции , если в точке
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
непрерывна на ![math]()
и дифференцируема на ![math]()
. Какое утверждение верно:
непрерывна на и дифференцируема на . Какое утверждение верно:
(1) если ![math]()
на ![math]()
, то ![math]()
возрастает на ![math]()
на , то возрастает на
(2) если ![math]()
на ![math]()
, то ![math]()
убывает на ![math]()
на , то убывает на
(3) если ![math]()
убывает на ![math]()
, то ![math]()
на ![math]()
убывает на , то на
(4) если ![math]()
, то ![math]()
локально убывает
, то локально убывает
(5) если ![math]()
, то ![math]()
локально убывает
, то локально убывает Пусть задана функция ![math]()
. На каких множествах существует неявная функция ![math]()
:
. На каких множествах существует неявная функция :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Последовательность ![math]()
сходится равномерно на множестве
сходится равномерно на множестве
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
интервал сходимости степенного ряда ![math]()
. Тогда множеством непрерывности суммы ряда является множество
интервал сходимости степенного ряда . Тогда множеством непрерывности суммы ряда является множество
(1) ![math]()
(2) вся числовая прямая
(3) ![math]()
Определите множества ![math]()
, ![math]()
если ![math]()
, ![math]()
, если
, 
если 
, 
, если
(1) ![math]()
, ![math]()
, 
(2) ![math]()
(3) ![math]()
Пусть ![math]()
- внешняя точка множества ![math]()
. Тогда ![math]()
- внешняя точка множества . Тогда
(1) принадлежит множеству ![math]()
(2) принадлежит множеству ![math]()
(3) граничная точка множества ![math]()
(4) граничная точка множества ![math]()
(5) предельная точка множества ![math]()
(6) предельная точка множества ![math]()
Пусть ![math]()
. Тогда
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
. ![math]()
и ![math]()
. Тогда функция ![math]()
имеет предел и он равен
. и . Тогда функция 
имеет предел и он равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
для функции ![math]()
является точкой разрыва
для функции 
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть задана функция ![math]()
. Тогда
. Тогда
(1) ![math]()
дифференцируема на ![math]()
дифференцируема на 
(2) ![math]()
непрерывна на ![math]()
непрерывна на 
(3) ![math]()
равномерно непрерывна на ![math]()
равномерно непрерывна на
(4) ![math]()
ограничена на ![math]()
ограничена на Пусть ![math]()
непрерывна в окрестности точки ![math]()
и ![math]()
. Пусть существует единственная неявная функция ![math]()
. Тогда
непрерывна в окрестности точки и 
. Пусть существует единственная неявная функция . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
может равняться 0
может равняться 0 Пусть последовательность ![math]()
равномерно сходится к непрерывной ![math]()
на множестве ![math]()
. Какие утверждения верны:
равномерно сходится к непрерывной на множестве . Какие утверждения верны:
(1) ![math]()
непрерывны на ![math]()
непрерывны на
(2) ![math]()
могут быть непрерывны на ![math]()
могут быть непрерывны на
(3) ![math]()
могут быть разрывны на ![math]()
могут быть разрывны на
(4) ![math]()
разрывны на ![math]()
разрывны на Пусть задан ряд ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) радиус сходимости ряда равен 1
(2) интервал сходимости ряда – множество ![math]()
(3) на концах интервала сходимости ряд расходится
(4) ряд сходится равномерно на ![math]()
Сколько существует отображений множества из
n элементов в множество из m элементов?
(1) nm
(2) n / m
(3) mn
(4) m / n
Замыканием ![math]()
открытого шара ![math]()
является множество
открытого шара 
является множество
(1) ![math]()
(2) ![math]()
(3) ![math]()
Если ![math]()
- предельная точка множества ![math]()
, то
- предельная точка множества , то
(1) ![math]()
(2) ![math]()
(3) ![math]()
Функция ![math]()
называется непрерывной в точке ![math]()
, если
называется непрерывной в точке , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Предел ![math]()
существует и равен
существует и равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
непрерывна на ![math]()
. Какие утверждения верны:
непрерывна на . Какие утверждения верны:
(1) если ![math]()
, то ![math]()
равномерно непрерывна на ![math]()
, то равномерно непрерывна на
(2) если ![math]()
, то ![math]()
равномерно непрерывна на ![math]()
, то равномерно непрерывна на
(3) если ![math]()
равномерно непрерывна на ![math]()
, то ![math]()
равномерно непрерывна на , то
(4) если ![math]()
не равномерно непрерывна на ![math]()
, то ![math]()
не равномерно непрерывна на , то 
Пусть задана неявная функция ![math]()
. Уравнение касательной в точке ![math]()
:
. Уравнение касательной в точке :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функциональный ряд называется сходящимся в точке ![math]()
, если
, если
(1) числовой ряд ![math]()
сходится
сходится
(2) числовой ряд ![math]()
расходится
расходится
(3) ![math]()
(4) ![math]()
Уравнение ![math]()
является
является
(1) линейным уравнением
(2) уравнением с разделяющимися переменными
(3) однородным уравнением
Запишите бесконечную периодическую десятичную дробь ![math]()
в в виде ![math]()
, если ![math]()
и ![math]()
- натуральные числа, не имеющие общих делителей.
в в виде , если и 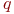- натуральные числа, не имеющие общих делителей.
(1) 29/22
(2) 1/6
(3) 13/18
(4) 1/18
Множество ![math]()
является замкнутым, если
является замкнутым, если
(1) некоторые его точки внутренние
(2) любая его точка внутренняя
(3) любая точка из его дополнения ![math]()
внутренняя
внутренняя
(4) некоторые точки из его дополнения ![math]()
внутренние
внутренние Пусть ![math]()
сходящаяся. Какие утверждения верны:
сходящаяся. Какие утверждения верны:
(1) множество частичных пределов ![math]()
бесконечно
бесконечно
(2) множество частичных пределов ![math]()
состоит из ![math]()
элементов
состоит из 
элементов
(3) множество частичных пределов ![math]()
состоит из одного элемента
состоит из одного элемента
(4) множество частичных пределов ![math]()
- пустое множество
- пустое множество Пусть функции ![math]()
. Какие условия достаточны для того, чтобы функция ![math]()
была непрерывной в точке ![math]()
:
. Какие условия достаточны для того, чтобы функция 
была непрерывной в точке 
:
(1) ![math]()
непрерывна в ![math]()
и ![math]()
непрерывна в ![math]()
непрерывна в и непрерывна в
(2) ![math]()
непрерывна в ![math]()
или ![math]()
непрерывна в ![math]()
непрерывна в или непрерывна в
(3) ![math]()
(4) ![math]()
Угловой коэффициент касательной, проведенной к кривой ![math]()
в точке с абсциссой ![math]()
, равен
в точке с абсциссой , равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Каким свойством обладает многочлен Тейлора ![math]()
функции ![math]()
:
функции :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
является точкой локального минимума для функции ![math]()
, если существует окрестность ![math]()
:
является точкой локального минимума для функции , если существует окрестность :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какое множество является областью сходимости ряда ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Если дифференциальное уравнение ![math]()
имеет решение ![math]()
, то
имеет решение , то
(1) оно единственно
(2) существует бесконечно много решений
(3) существует хотя бы одно решение
(4) область определения решения ![math]()
Сравните следующие действительные числа: 3, 3 и 3, 298
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть множество ![math]()
замкнуто. Какие утверждения верны:
замкнуто. Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
(7) ![math]()
Пусть задана функция ![math]()
. Пусть существует обратная к ней функция ![math]()
. Какие утверждения справедливы:
. Пусть существует обратная к ней функция 
. Какие утверждения справедливы:
(1) ![math]()
(2) ![math]()
(3) ![math]()
непрерывна в ![math]()
и ![math]()
непрерывна в ![math]()
непрерывна в и 
непрерывна в
(4) ![math]()
непрерывна в ![math]()
или ![math]()
непрерывна в ![math]()
непрерывна в или непрерывна в Уравнение касательной к графику функции ![math]()
в точке ![math]()
в точке 
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Функция ![math]()
называется выпуклой на множестве ![math]()
(выпуклое), если
называется выпуклой на множестве (выпуклое), если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- особая точка для дифференцируемой функции ![math]()
. Какое условие является достаточным для того, чтобы ![math]()
была точкой локального максимума:
- особая точка для дифференцируемой функции . Какое условие является достаточным для того, чтобы была точкой локального максимума:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
Какая функция является суммой ряда ![math]()
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Что является общим решением дифференциального уравнения ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Найти ![math]()
и ![math]()
, если множество ![math]()
состоит из элементов, являющихся членами последовательности ![math]()
, где ![math]()
и 
, если множество состоит из элементов, являющихся членами последовательности 
, где 
(1) 4 и 0
(2) 2 и 1
(3) 1 и 1/2
(4) 1 и 0
- множество иррациональных чисел. Какие утверждения верны:
(1) ![math]()
содержит хотя бы одну изолированную точку
содержит хотя бы одну изолированную точку
(2) любая его точка является граничной
(3) ![math]()
- замкнутое множество
- замкнутое множество
(4) ![math]()
не является открытым
не является открытым Пусть числовая последовательность ![math]()
сходится и ![math]()
. Тогда
сходится и 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть задана функция ![math]()
, ![math]()
- компактное множество. Какой может быть функция ![math]()
на множестве ![math]()
:
, - компактное множество. Какой может быть функция на множестве :
(1) разрывная и неограниченная
(2) непрерывная и ограниченная
(3) непрерывная и неограниченная
Пусть функция ![math]()
дифференцируема в точке ![math]()
и обратима в ![math]()
и ![math]()
- обратная функция. Какие утверждения справедливы:
дифференцируема в точке и обратима в 
и - обратная функция. Какие утверждения справедливы:
(1) обратная функция дифференцируема в точке ![math]()
(2) обратная функция не дифференцируема в точке ![math]()
(3) обратная функция может быть дифференцируемой в точке ![math]()
Функция ![math]()
называется дифференцируемой в точке ![math]()
, если
называется дифференцируемой в точке 
, если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
является точкой локального минимума для функции ![math]()
при условиях ![math]()
, если для ![math]()
существует окрестность ![math]()
:
является точкой локального минимума для функции при условиях , если для существует окрестность :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функциональный ряд ![math]()
сходится равномерно к функции ![math]()
на множестве ![math]()
, если
сходится равномерно к функции на множестве , если
(1) последовательность частичных сумм ![math]()
равномерно сходится к ![math]()
на ![math]()
равномерно сходится к на
(2) последовательность частичных сумм ![math]()
сходится к ![math]()
на ![math]()
сходится к на
(3) последовательность ![math]()
равномерно сходится к ![math]()
на ![math]()
равномерно сходится к на
(4) последовательность ![math]()
сходится к ![math]()
на ![math]()
сходится к на Какие утверждения для задачи Коши ![math]()
верны:
верны:
(1) если ![math]()
непрерывна в окрестности ![math]()
, то решение задачи Коши существует и единственно
непрерывна в окрестности , то решение задачи Коши существует и единственно
(2) если ![math]()
ограничена в окрестности ![math]()
, то решение задачи Коши существует и единственно
ограничена в окрестности , то решение задачи Коши существует и единственно
(3) если ![math]()
непрерывна и не удовлетворяет условию Липшица в окрестности ![math]()
, то решение задачи Коши существует, но он не единственно
непрерывна и не удовлетворяет условию Липшица в окрестности , то решение задачи Коши существует, но он не единственно Множество рациональных чисел обозначается через
(1) R
(2) Q
(3) Z
(4) Y
Пусть ![math]()
. Какое множество является множеством граничных точек ![math]()
:
. Какое множество является множеством граничных точек :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовые последовательности ![math]()
и ![math]()
сходятся и ![math]()
. Тогда последовательность ![math]()
сходится и ее предел равен
и сходятся и 
. Тогда последовательность 
сходится и ее предел равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть задана функция ![math]()
- компактное множество. Какой может быть функция ![math]()
на множестве ![math]()
:
- компактное множество. Какой может быть функция на множестве :
(1) ![math]()
непрерывная и ![math]()
не достигает своих верхней и нижней грани на ![math]()
непрерывная и не достигает своих верхней и нижней грани на
(2) ![math]()
разрывная и ![math]()
не достигает своих верхней и нижней грани на ![math]()
разрывная и не достигает своих верхней и нижней грани на
(3) ![math]()
разрывная и ![math]()
достигает своих верхней и нижней грани на ![math]()
разрывная и достигает своих верхней и нижней грани на
(4) ![math]()
непрерывная и ![math]()
достигает своей верхней или нижней грани на ![math]()
непрерывная и достигает своей верхней или нижней грани на Точка ![math]()
является точкой локального максимума функции ![math]()
, если
является точкой локального максимума функции , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
дифференцируема в точке ![math]()
. Какие утверждения верны:
дифференцируема в точке . Какие утверждения верны:
(1) ![math]()
- внутренняя точка области определения
- внутренняя точка области определения
(2) ![math]()
может быть граничной точкой области определения
может быть граничной точкой области определения
(3) существуют частные производные в точке ![math]()
по каждому аргументу
по каждому аргументу
(4) частные производные существуют и непрерывны
(5) функция ![math]()
непрерывна в точке ![math]()
непрерывна в точке
(6) функция ![math]()
может быть разрывна в точке ![math]()
может быть разрывна в точке Пусть задана функция ![math]()
при условии ![math]()
. Пусть задана функция Лагранжа ![math]()
. Тогда особая точка ![math]()
будет точкой условного локального максимума, если для любого допустимого сдвига
при условии . Пусть задана функция Лагранжа . Тогда особая точка будет точкой условного локального максимума, если для любого допустимого сдвига
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
знакопеременная
знакопеременная Пусть ряд ![math]()
сходится равномерно на множестве ![math]()
. Какие утверждения верны:
сходится равномерно на множестве . Какие утверждения верны:
(1) существует сходящийся числовой ряд ![math]()
, для которого ![math]()
, для которого 
(2) может не существовать сходящийся числовой ряд ![math]()
такой, что ![math]()
такой, что
(3) последовательность ![math]()
сходится равномерно к ![math]()
на ![math]()
сходится равномерно к 
на
(4) последовательность ![math]()
может не сходиться равномерно к ![math]()
на ![math]()
может не сходиться равномерно к на Пусть у задачи Коши ![math]()
решение ![math]()
является продолжением решения ![math]()
. Тогда
решение является продолжением решения . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Интервал значений (0;1) является примером
(1) неограниченного множества
(2) ограниченного множества
(3) множества, ограниченного снизу
(4) множества, ограниченного сверху
Пусть числовая последовательность ![math]()
сходится, ![math]()
расходится. Тогда последовательность ![math]()
сходится, расходится. Тогда последовательность 
(1) всегда сходится
(2) всегда расходится
(3) может сходится или расходится
Пусть задана непрерывная числовая функция ![math]()
. Пусть ![math]()
и ![math]()
. Тогда
. Пусть 
и 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- точка локального экстремума функции ![math]()
. Тогда производная
- точка локального экстремума функции . Тогда производная
(1) ![math]()
не существует
не существует
(2) ![math]()
(3) ![math]()
(4) ![math]()
или не существует
или не существует
(5) ![math]()
или не существует
или не существует Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) непрерывна на ![math]()
(2) существуют ![math]()
(3) ![math]()
дифференцируема в ![math]()
дифференцируема в
(4) ![math]()
непрерывны в ![math]()
непрерывны в Пусть ![math]()
не является точкой экстремума функции ![math]()
при условии ![math]()
. Тогда линия уровня ![math]()
пересекает кривую ![math]()
под углом
не является точкой экстремума функции при условии . Тогда линия уровня пересекает кривую под углом
(1) ![math]()
(2) ![math]()
(3) ![math]()
Какой числовой ряд нужно использовать для доказательства равномерной сходимости ряда ![math]()
по признаку Вейерштрасса:
по признаку Вейерштрасса:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана задача Коши ![math]()
. Тогда
. Тогда
(1) в любой окрестности ![math]()
выполнено условие Липшица
выполнено условие Липшица
(2) через начало координат проходит единственная интегральная кривая данного уравнения
(3) решение задачи существует, но не единственно
Если ![math]()
, то
, то
(1) ![math]()
, ![math]()
, 
(2) ![math]()
, ![math]()
, 
(3) ![math]()
, ![math]()
, 
(4) ![math]()
, ![math]()
, 
Пусть числовая последовательность ![math]()
ограничена. ![math]()
- множество частичных пределов последовательности ![math]()
. Какие утверждения верны:
ограничена. - множество частичных пределов последовательности . Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
состоит только из одного элемента
состоит только из одного элемента На каком множестве функция ![math]()
является непрерывной:
является непрерывной:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовая последовательность ![math]()
сходится и ![math]()
. ![math]()
-множество частичных пределов ![math]()
. Какие утверждения верны:
сходится и 
. -множество частичных пределов . Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
. Тогда она
. Тогда она
(1) непрерывна на всей плоскости, кроме прямой ![math]()
(2) достигает свои точные грани на всей плоскости
(3) обращается в ноль на отрезке ![math]()
Пусть ![math]()
- неограниченная последовательность в пространстве ![math]()
. Какие утверждения верны:
- неограниченная последовательность в пространстве . Какие утверждения верны:
(1) ![math]()
расходится
расходится
(2) из ![math]()
можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность
(3) в некоторой окрестности лежит бесконечное число точек ![math]()
Пусть ![math]()
, ![math]()
- множество частичных пределов ![math]()
. Какие утверждения верны:
, - множество частичных пределов . Какие утверждения верны:
(1) ![math]()
неубывающая
неубывающая
(2) ![math]()
ограниченная
ограниченная
(3) ![math]()
сходится
сходится
(4) ![math]()
(5) ![math]()
Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) ![math]()
ограничена
ограничена
(2) ![math]()
неубывающая
неубывающая
(3) ![math]()
сходится
сходится Найдите предел последовательности ![math]()
, если ![math]()
. Выберете правильные ответ:
, если . Выберете правильные ответ:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
непрерывная функция. Каким должно быть множество ![math]()
, чтобы множество ![math]()
было компактным
непрерывная функция. Каким должно быть множество , чтобы множество было компактным
(1) компактное множество
(2) замкнутое, но не ограниченное
(3) ограниченное, но не замкнутое
(4) замкнутое и ограниченное
Линиями уровня функции ![math]()
являются
являются
(1) семейство парабол
(2) семейство гипербол
(3) концентрические круги
(4) ![math]()
Пусть ![math]()
- множество сходимости последовательности ![math]()
. Функция ![math]()
является пределом последовательности ![math]()
. Тогда она
- множество сходимости последовательности . Функция является пределом последовательности . Тогда она
(1) определена на множестве ![math]()
(2) определена на множестве ![math]()
(3) ![math]()
(4) ![math]()
(5) непрерывна на ![math]()
, если ![math]()
непрерывны на ![math]()
, если непрерывны на
(6) разрывна на ![math]()
, если ![math]()
разрывна на ![math]()
, если разрывна на Какие утверждения верны:
(1) степенной ряд может не быть функциональным
(2) функциональный ряд может не быть степенным
(3) каждый степенной ряд имеет ненулевой интервал сходимости
(4) интервал сходимости степенного ряда может равняться одной точке
(5) интервал сходимости степенного ряда никогда не совпадает с числовой прямой
Расстояние ![math]()
в ![math]()
вычисляется по формуле
в вычисляется по формуле
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть задана последовательность ![math]()
в ![math]()
и ![math]()
.Тогда (по определению) это последовательность называется
в и .Тогда (по определению) это последовательность называется
(1) сходящейся
(2) ограниченной
(3) фундаментальной
Функция ![math]()
не является равномерно непрерывной на множестве ![math]()
, если
не является равномерно непрерывной на множестве , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Геометрический смысл теоремы Лагранжа состоит в том, что существует хотя бы одна точка графика функции ![math]()
, в которой касательная
, в которой касательная
(1) параллельна оси ![math]()
(2) перпендикулярна оси ![math]()
(3) параллельна хорде ![math]()
Пусть функция ![math]()
задана на множестве ![math]()
. Тогда
задана на множестве 
. Тогда
(1) функция достигает на множестве ![math]()
наибольшего значения
наибольшего значения
(2) функция достигает на множестве ![math]()
наименьшего значения
наименьшего значения
(3) функция ограничена на ![math]()
Найти предел последовательности ![math]()
на множестве ![math]()
:
на множестве 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
- интервал сходимости степенного ряда ![math]()
. Тогда
- интервал сходимости степенного ряда . Тогда
(1) ряд может сходиться или расходиться в точке ![math]()
(2) в точке ![math]()
ряд может сходиться или расходится
ряд может сходиться или расходится
(3) если ![math]()
, то ряд расходится
, то ряд расходится Какая операция отображена на рисунке?![files]()
(1) пересечение множеств
(2) разность множеств
(3) объединение множеств
(4) симметрическая разность
Множество ![math]()
называется
называется
(1) открытым шаром радиуса ![math]()
(2) замкнутым шаром радиуса ![math]()
(3) открытым параллелепипедом
(4) замкнутым параллелепипедом
Последовательность ![math]()
в пространстве ![math]()
называется ограниченной, если все ее элементы содержатся в
в пространстве называется ограниченной, если все ее элементы содержатся в
(1) замкнутом множестве
(2) открытом множестве
(3) замкнутом шаре
(4) замкнутом параллелепипеде
Пусть последовательность ![math]()
в пространстве ![math]()
сходится и ![math]()
. Какие утверждения верны:
в пространстве сходится и . Какие утверждения верны:
(1) ![math]()
фундаментальная
фундаментальная
(2) ![math]()
ограниченная
ограниченная
(3) ![math]()
Пусть ![math]()
. Какие утверждения справедливы:
. Какие утверждения справедливы:
(1) ![math]()
- непрерывна на ![math]()
- равномерно непрерывна на ![math]()
- непрерывна на 
- равномерно непрерывна на
(2) ![math]()
- равномерно непрерывна на ![math]()
- непрерывна на ![math]()
- равномерно непрерывна на - непрерывна на
(3) ![math]()
- непрерывна на ![math]()
, ![math]()
- компакт ![math]()
- равномерно непрерывна на ![math]()
- непрерывна на , - компакт 
- равномерно непрерывна на
(4) ![math]()
- равномерно непрерывна на ![math]()
, ![math]()
- компакт ![math]()
- непрерывна на ![math]()
- равномерно непрерывна на , - компакт - непрерывна на
(5) ![math]()
- непрерывна на ![math]()
, ![math]()
- замкнутое - равномерно непрерывна на ![math]()
- непрерывна на , - замкнутое - равномерно непрерывна на
(6) ![math]()
- равномерно непрерывна на ![math]()
, ![math]()
- замкнутое ![math]()
- непрерывна на ![math]()
- равномерно непрерывна на , - замкнутое - непрерывна на Определить градиент функции ![math]()
в точке ![math]()
и найти его модуль (длину):
в точке и найти его модуль (длину):
(1) ![math]()
(2) ![math]()
(3) ![math]()
Последовательность ![math]()
сходится к ![math]()
неравномерно на множестве ![math]()
, если она
сходится к неравномерно на множестве , если она
(1) сходится к ![math]()
и ![math]()
и 
(2) не сходится к ![math]()
и ![math]()
и
(3) сходится к ![math]()
и ![math]()
и 
(4) не сходится к ![math]()
и ![math]()
и Степенной ряд сходится равномерно
(1) в интервале сходимости
(2) на компактном подмножестве интервала сходимости
(3) на замкнутом подмножестве интервала сходимости
(4) на ограниченном подмножестве интервала сходимости
Ограниченное множество - это
(1) множество, ограниченное снизу
(2) множество, ограниченное и сверху, и снизу
(3) множество, ограниченное сверху
(4) пустое множество
Отметьте верные утверждения:
(1) последовательность вложенных интервалов в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(2) последовательность вложенных отрезков в ![math]()
имеет пустое пересечение
имеет пустое пересечение
(3) последовательность вложенных отрезков в ![math]()
имеет непустое пересечение
имеет непустое пересечение
(4) последовательность вложенных интервалов в ![math]()
имеет пустое пересечение
имеет пустое пересечение Пусть ![math]()
. Тогда внутри каждой окрестности ![math]()
-
. Тогда внутри каждой окрестности -
(1) бесконечное, начиная с некоторого номера, число точек ![math]()
(2) конечное число точек ![math]()
(3) все точки ![math]()
Точка ![math]()
называется пределом функции ![math]()
при стремлениии ![math]()
, если
называется пределом функции 
при стремлениии , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Число ![math]()
является пределом ![math]()
числовой функции ![math]()
. Какие утверждения верны:
является пределом 
числовой функции . Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Функция ![math]()
называется возрастающей на ![math]()
, если ![math]()
называется возрастающей на , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задана функция ![math]()
. Тогда частные производные 2 порядка равны:
. Тогда частные производные 2 порядка равны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Последовательность ![math]()
сходится к ![math]()
на множестве ![math]()
. Тогда
сходится к на множестве . Тогда
(1) ![math]()
сходится равномерно к ![math]()
на ![math]()
сходится равномерно к на
(2) ![math]()
сходится неравномерно к ![math]()
на ![math]()
сходится неравномерно к на
(3) ![math]()
сходится равномерно к ![math]()
на ![math]()
, если ![math]()
сходится равномерно к на , если
(4) ![math]()
сходится равномерно к ![math]()
на ![math]()
, если ![math]()
сходится равномерно к на , если Если ![math]()
, то интервал сходимости ряда ![math]()
, то интервал сходимости ряда
(1) равен числовой прямой
(2) равен интервалу ![math]()
(3) вырождается в одну точку ![math]()
В каком отношении находятся множества ![math]()
и ![math]()
, если ![math]()
, ![math]()
и , если 
, 
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется граничной точкой множества ![math]()
, если
называется граничной точкой множества , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Пусть числовая последовательность ![math]()
- множество частичных пределов ![math]()
. Верхний предел числовой последовательности ![math]()
- это
- множество частичных пределов . Верхний предел числовой последовательности - это
(1) верхняя грань множества ![math]()
, большая ![math]()
, большая
(2) нижняя грань множества ![math]()
, меньшая ![math]()
, меньшая
(3) ![math]()
(4) ![math]()
Пусть ![math]()
. Тогда
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
называется точкой разрыва функции ![math]()
с конечным скачком функции, если в точке ![math]()
называется точкой разрыва функции с конечным скачком функции, если в точке
(1) ![math]()
(2) ![math]()
(3) ![math]()
Сколько непрерывных неявных функций вида ![math]()
определяет уравнение ![math]()
в окрестности точки ![math]()
:
определяет уравнение 
в окрестности точки 
:
(1) одна
(2) ни одной
(3) две
(4) четыре
Последовательность ![math]()
сходится неравномерно на множестве
сходится неравномерно на множестве
(1) ![math]()
(2) ![math]()
(3) ![math]()
Какое множество является множеством непрерывности суммы ряда ![math]()
(1) ![math]()
(2) вся числовая прямая
(3) ![math]()
Какие из утверждений верны?
(1) ![math]()
, ![math]()
, 
(2) если ![math]()
- пустое множество, то ![math]()
- пустое множество, то 
(3) если ![math]()
, то ![math]()
, ![math]()
, то 
, 
Пусть ![math]()
- внешняя точка множества ![math]()
. Тогда
- внешняя точка множества . Тогда
(1) ![math]()
может быть предельной точкой множества ![math]()
может быть предельной точкой множества
(2) ![math]()
может не быть предельной точкой множества ![math]()
может не быть предельной точкой множества
(3) ![math]()
(4) ![math]()
может быть изолированной точкой множества ![math]()
может быть изолированной точкой множества
(5) ![math]()
может быть внутренней точкой множества ![math]()
может быть внутренней точкой множества Пусть ![math]()
. ![math]()
и ![math]()
. Тогда функция ![math]()
имеет предел и он равен
. и 
. Тогда функция 
имеет предел и он равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
для функции ![math]()
является точкой разрыва
для функции 
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть выполнены условия существования теоремы о неявной функции. Тогда её производная ![math]()
равна:
равна:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть задан ряд ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) интервал сходимости ряда – множество ![math]()
(2) на концах интервала сходимости ряд сходится
(3) на концах интервала сходимости ряд расходится
(4) ряд сходится равномерно на ![math]()
(5) сумма ряда неограниченна в окрестности 1
Множество ![math]()
состоит из трех элементов, а множество ![math]()
- из двух элементов. Сколько существует отображений ![math]()
в ![math]()
?
состоит из трех элементов, а множество - из двух элементов. Сколько существует отображений в ?
(1) 6
(2) 8
(3) 1
(4) 4
Границей ![math]()
открытого шара ![math]()
является множество
открытого шара является множество
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть ![math]()
сходящаяся и ![math]()
. Тогда
сходящаяся и 
. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
Предел ![math]()
существует и равен
существует и равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функция ![math]()
непрерывна на ![math]()
, дифференцируема на ![math]()
и ![math]()
. Какие утверждения верны:
непрерывна на , дифференцируема на и 
. Какие утверждения верны:
(1) ![math]()
равномерно непрерывна на ![math]()
равномерно непрерывна на
(2) если ![math]()
ограничена на ![math]()
, то ![math]()
ограничена на , то
(3) если ![math]()
не ограничена на ![math]()
, то ![math]()
не ограничена на , то 
Пусть ![math]()
- множество сходимости ряда ![math]()
. Функция ![math]()
является суммой ряда. Тогда она
- множество сходимости ряда . Функция является суммой ряда. Тогда она
(1) определена на множестве ![math]()
(2) определена на множестве ![math]()
(3) ![math]()
(4) ![math]()
(5) непрерывна на ![math]()
, если ![math]()
непрерывны на ![math]()
, если непрерывны на
(6) разрывна на ![math]()
, если ![math]()
разрывна на ![math]()
, если разрывна на Уравнение ![math]()
является
является
(1) линейным уравнением
(2) уравнением с разделяющимися переменными
(3) однородным уравнением
Запишите бесконечную периодическую десятичную дробь ![math]()
в в виде ![math]()
, если ![math]()
и ![math]()
- натуральные числа, не имеющие общих делителей.
в в виде , если и 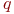- натуральные числа, не имеющие общих делителей.
(1) 1/125
(2) 1/8
(3) 1/4
(4) 0
Множество ![math]()
называется ограниченным, если оно
называется ограниченным, если оно
(1) содержится в некоторой окрестности ![math]()
(2) любая окрестность ![math]()
содержит точки множества ![math]()
содержит точки множества
(3) содержится в некотором открытом множестве
Множество частичных пределов ![math]()
состоит из одного элемента ![math]()
. Тогда последовательность ![math]()
состоит из одного элемента 
. Тогда последовательность
(1) расходится
(2) сходится и ![math]()
(3) сходится и ![math]()
Пусть функции ![math]()
. Какие условия достаточны для того, чтобы функция ![math]()
была непрерывной в точке ![math]()
:
. Какие условия достаточны для того, чтобы функция была непрерывной в точке :
(1) ![math]()
непрерывна в ![math]()
и ![math]()
непрерывна в ![math]()
непрерывна в и непрерывна в
(2) ![math]()
непрерывна в ![math]()
или ![math]()
непрерывна в ![math]()
непрерывна в или непрерывна в
(3) ![math]()
(4) ![math]()
Угловой коэффициент нормали, проведенной к кривой ![math]()
в точке с абсциссой ![math]()
, равен
в точке с абсциссой , равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Как связаны многочлен Тейлора ![math]()
функции ![math]()
, сама функция и остаточный член ![math]()
:
функции , сама функция и остаточный член 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
Точка ![math]()
не является точкой локального максимума для функции ![math]()
, если для любой окрестности ![math]()
:
не является точкой локального максимума для функции , если для любой окрестности :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какое множество является областью сходимости ряда ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Сравните следующие действительные числа: 3, 1416 и 3, 14159
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какие из следующих множеств являются открытыми:
(1) пустое множество ![math]()
(2) пространство ![math]()
(3) окрестность ![math]()
(4) отрезок ![math]()
(5) пересечение конечного числа открытых множеств
(6) пересечение бесконечного числа открытых множеств
(7) пересечение любой совокупности открытых множеств
(8) объединение любой совокупности открытых множеств
(9) объединение бесконечного числа открытых множеств
(10) объединение конечного числа открытых множеств
Пусть задана функция ![math]()
. Пусть существует обратная к ней функция ![math]()
. Какие утверждения справедливы:
. Пусть существует обратная к ней функция . Какие утверждения справедливы:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Уравнение касательной к графику функции ![math]()
в точке ![math]()
в точке
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
(6) ![math]()
Функция ![math]()
выпуклая на множестве ![math]()
(выпуклое). Верно ли, что она
выпуклая на множестве (выпуклое). Верно ли, что она
(1) непрерывная на ![math]()
(2) дифференцируемая на ![math]()
(3) может быть разрывной на ![math]()
(4) может быть не дифференцируемой на ![math]()
(5) разрывна на ![math]()
(6) не дифференцируема на ![math]()
Пусть ![math]()
- особая точка для дифференцируемой функции ![math]()
. Какое условие является достаточным для того, чтобы ![math]()
была точкой локального минимума:
- особая точка для дифференцируемой функции . Какое условие является достаточным для того, чтобы была точкой локального минимума:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
Какая функция является суммой ряда ![math]()
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Что является общим решением дифференциального уравнения ![math]()
:
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Существуют ли действительные корни уравнения ![math]()
(1) существуют
(2) не существуют
- множество натуральных чисел. Какие утверждения верны:
(1) 1 – предельная точка множества ![math]()
(2) ![math]()
ограниченное множество
ограниченное множество
(3) ![math]()
состоит из изолированных точек
состоит из изолированных точек
(4) ![math]()
замкнутое множество
замкнутое множество
(5) ![math]()
счетное множество
счетное множество Пусть числовые последовательности: ![math]()
. Тогда ![math]()
. Тогда 
(1) расходится
(2) сходится и ![math]()
(3) сходится и ![math]()
Точка ![math]()
не является точкой локального минимума функции ![math]()
, если
не является точкой локального минимума функции , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Какие условия являются достаточными для дифференцируемости функции ![math]()
в точке ![math]()
:
в точке :
(1) ![math]()
непрерывна в точке ![math]()
непрерывна в точке
(2) существуют частные производные в точке ![math]()
по каждому аргументу
по каждому аргументу
(3) Частные производные в точке ![math]()
по каждому аргументу существуют и непрерывны в точке ![math]()
по каждому аргументу существуют и непрерывны в точке Пусть задана функция ![math]()
при условии ![math]()
. Пусть задана функция Лагранжа ![math]()
. Тогда особая точка ![math]()
будет точкой условного локального минимума, если для любого допустимого сдвига
при условии . Пусть задана функция Лагранжа . Тогда особая точка будет точкой условного локального минимума, если для любого допустимого сдвига
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
знакопеременная
знакопеременная Какие утверждения верны:
(1) сумма функционального ряда с непрерывными членами может быть разрывной функцией
сумма равномерно сходящегося функционального ряда с непрерывными членами может быть разрывной функцией
(2) сумма функционального ряда может быть разрывной функцией
(3) функциональный ряд равномерно сходится в области сходимости сумма равномерно сходящегося функционального ряда с непрерывными членами может быть разрывной функцией
(4) сумма функционального ряда с ограниченными членами может быть неограниченной функцией
Решение задачи Коши ![math]()
может быть продолжено
может быть продолжено
(1) на всю область определения ![math]()
(2) до границы замкнутого подмножества ![math]()
(3) до границы компактного подмножества ![math]()
(4) до границы ограниченного подмножества ![math]()
Множество натуральных чисел 1,2,3... является примером
(1) множества, ограниченного снизу
(2) множества, ограниченного сверху
(3) неограниченного множества
(4) ограниченного множества
Пусть числовая последовательность ![math]()
сходится, ![math]()
расходится. Тогда последовательность ![math]()
сходится, расходится. Тогда последовательность
(1) всегда сходится
(2) всегда расходится
(3) может сходиться или расходиться
Какие множества могут быть множеством значений непрерывной числовой функции ![math]()
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) ![math]()
Пусть ![math]()
- точка, в которой ![math]()
или не существует. Какие утверждения верны:
- точка, в которой или не существует. Какие утверждения верны:
(1) ![math]()
- точка локального экстремума
- точка локального экстремума
(2) ![math]()
- точка возможного экстремума
- точка возможного экстремума
(3) ![math]()
не является точкой экстремума
не является точкой экстремума Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) непрерывна на ![math]()
(2) ![math]()
(3) ![math]()
дифференцируема в ![math]()
дифференцируема в
(4) ![math]()
непрерывны в ![math]()
непрерывны в Пусть ![math]()
точка экстремума функции ![math]()
при условии ![math]()
. Тогда
точка экстремума функции при условии . Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
линейно зависимы
линейно зависимы
(4) ![math]()
линейно независимы
линейно независимы
(5) ![math]()
перпендикулярны
перпендикулярны Пусть задана задача Коши ![math]()
. Тогда
. Тогда
(1) уравнение является линейным неоднородным
(2) максимальное решение может быть задано на интервале ![math]()
(3) функция ![math]()
является максимальным решением для ![math]()
является максимальным решением для 
(4) функция ![math]()
является максимальным решением для ![math]()
является максимальным решением для 
Решите неравенство: ![math]()
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовая последовательность ![math]()
ограничена. ![math]()
- множество частичных пределов последовательности ![math]()
. Какие утверждения верны:
ограничена. - множество частичных пределов последовательности . Какие утверждения верны:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
На каком множестве функция ![math]()
является непрерывной:
является непрерывной:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
, лежащая на кривой ![math]()
, является точкой условного максимума, если существует окрестность ![math]()
:
, лежащая на кривой , является точкой условного максимума, если существует окрестность 
:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть функциональный ряд ![math]()
сходится равномерно к функции ![math]()
на множестве ![math]()
. Тогда
сходится равномерно к функции на множестве . Тогда
(1) ряд сходится к ![math]()
на ![math]()
на
(2) область сходимости ряда содержит множество ![math]()
(3) область сходимости ряда содержится в множестве ![math]()
(4) ![math]()
(5) последовательность ![math]()
сходится равномерно к ![math]()
на ![math]()
сходится равномерно к на
(6) последовательность ![math]()
сходится к ![math]()
на ![math]()
сходится к на Если ![math]()
непрерывна и удовлетворяет условию Липшица в некоторой окрестности ![math]()
и ![math]()
- решения задачи Коши ![math]()
, то
непрерывна и удовлетворяет условию Липшица в некоторой окрестности и 
- решения задачи Коши , то
(1) ![math]()
в некоторой окрестности ![math]()
в некоторой окрестности
(2) ![math]()
на всей области определения
на всей области определения Принцип непрерывности Дедекинда
(1) для каждого сечения множества действительных чисел существует число, производящее это сечение
(2) всякая система вложенных отрезков имеет непустое пересечение, то есть существует по крайней мере одно число, которое принадлежит всем отрезкам данной системы
(3) у всякого числового множества верхняя (нижняя) грань единственна
Пусть ![math]()
. Какое множество является множеством изолированных точек ![math]()
:
. Какое множество является множеством изолированных точек :
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть числовые последовательности ![math]()
и ![math]()
сходятся и ![math]()
. Тогда последовательность ![math]()
сходится и ее предел равен
и сходятся и 
. Тогда последовательность 
сходится и ее предел равен
(1) ![math]()
(2) ![math]()
(3) ![math]()
Пусть задана непрерывная функция ![math]()
, ![math]()
- компактное множество. Тогда
, - компактное множество. Тогда
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- последовательность элементов компактного множества ![math]()
. Какие утверждения верны:
- последовательность элементов компактного множества 
. Какие утверждения верны:
(1) ![math]()
сходится
сходится
(2) из ![math]()
можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность
(3) множество частичных пределов ![math]()
и ![math]()
и 
(4) найдется частичный предел ![math]()
(5) ![math]()
ограниченная
ограниченная Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) ![math]()
сходится
сходится
(2) ![math]()
ограничена
ограничена
(3) ![math]()
- предел последовательности ![math]()
- предел последовательности
(4) ![math]()
- предельная точка множества значений последовательности
- предельная точка множества значений последовательности Найдите предел последовательности ![math]()
, если ![math]()
. Выберете правильные ответ:
, если 
. Выберете правильные ответ:
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Точка ![math]()
называется точкой разрыва функции ![math]()
второго рода, если в точке ![math]()
называется точкой разрыва функции второго рода, если в точке
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- изолированная точка множества ![math]()
. Какие утверждения верны:
- изолированная точка множества . Какие утверждения верны:
(1) ![math]()
открытое множество
открытое множество
(2) ![math]()
не открытое множество
не открытое множество
(3) ![math]()
замкнутое
замкнутое
(4) ![math]()
содержит граничные точки
содержит граничные точки
(5) ![math]()
предельная точка множества ![math]()
предельная точка множества
(6) ![math]()
Расстояние ![math]()
в ![math]()
вычисляется по формуле
в 
вычисляется по формуле
(1) ![math]()
(2) ![math]()
(3) ![math]()
Множество ![math]()
называется
называется
(1) открытым шаром радиуса ![math]()
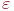
(2) замкнутым шаром радиуса ![math]()
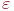
(3) открытым параллелепипедом
(4) замкнутым параллелепипедом
Точка ![math]()
называется изолированной точкой множества ![math]()
, если
называется изолированной точкой множества , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Отметьте верные утверждения:
(1) любое множество ![math]()
имеет граничные точки
имеет граничные точки
(2) любое множество ![math]()
имеет граничные точки
имеет граничные точки Множество ![math]()
называется компактным, если оно
называется компактным, если оно
(1) ограничено и замкнуто
(2) ограничено и открыто
(3) ограничено и содержит все свои предельные точки
(4) ограничено и содержит все свои граничные точки
Какие из следующих множеств являются замкнутыми:
(1) пространство ![math]()
(2) окрестность ![math]()
(3) множество предельных точек множества
(4) пересечение любой совокупности замкнутых множеств
(5) объединение любой совокупности замкнутых множеств
(6) объединение конечного числа замкнутых множеств
Расстояние ![math]()
в ![math]()
вычисляется по формуле
в вычисляется по формуле
(1) ![math]()
(2) ![math]()
(3) ![math]()
Окрестностью ![math]()
точки ![math]()
называется
точки называется
(1) открытый шар радиуса ![math]()
с центром в точке ![math]()
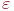с центром в точке
(2) замкнутый шар радиуса ![math]()
с центром в точке ![math]()
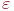с центром в точке Точка ![math]()
называется предельной точкой множества ![math]()
, если
называется предельной точкой множества , если
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
Пусть ![math]()
- предельная точка множества ![math]()
. Какие утверждения верны:
- предельная точка множества . Какие утверждения верны:
(1) ![math]()
может быть внутренней точкой множества ![math]()
может быть внутренней точкой множества
(2) ![math]()
может быть граничной точкой множества ![math]()
может быть граничной точкой множества
(3) ![math]()
может быть изолированной точкой множества ![math]()
может быть изолированной точкой множества
(4) в любой ее окрестности содержится бесконечно много точек множества ![math]()
(5) существует ее окрестность, в которой содержится только конечное число точек множества![math]()
Пусть ![math]()
– конечное множество. Тогда оно
– конечное множество. Тогда оно
(1) открытое множество
(2) замкнутое множество
(3) состоит из изолированных точек
(4) содержит предельные точки
(5) содержит граничные точки
Пусть ![math]()
. Какие утверждения верны:
. Какие утверждения верны:
(1) ![math]()
счетное множество
счетное множество
(2) ![math]()
имеет только 1 предельную точку
имеет только 1 предельную точку
(3) ![math]()
открытое множество
открытое множество