Главная /
Математика /
Основы теории вероятностей
Основы теории вероятностей - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Теория вероятностей относится к одному из разделов "чистой математики". Она строится на дедуктивных принципах, на основании опыта и умозаключений. Эта наука о возможных взаимоотношениях большого количества случайных событий.
Все ответы: Теория вероятностей относится к одному из разделов "чистой математики". Она строится на дедуктивных принципах, на основании опыта и умозаключений. Эта наука о возможных взаимоотношениях большого количества случайных событий.
Какие методы используют для обработки и интерпретации экспериментальных данных?
(1) вероятностно-статистический метод
(2) аналитический метод
(3) метод графиков
(4) экспериментальный метод
Произошли два события А и В. Было установлено, что выполняется: ![math]() . Что можно сказать о событиях А и В?
. Что можно сказать о событиях А и В?
 . Что можно сказать о событиях А и В?
. Что можно сказать о событиях А и В?
(1) события условно зависимые
(2) события зависимые
(3) события независимые
(4) события условно независимые
Одну монетку кидают 3 раза. Сколько вариантов возможных результатов? Ответ введите с точностью до целых
8
Дайте определение случайной величины
(1) появление некоторых числовых значений в результате эксперимента
(2) величина, принимающая в результате эксперимента одно только значение из некоторой их совокупности
(3) величина, принимающая в результате эксперимента одно только значение из некоторой их совокупности и неизвестное заранее, какое именно
(4) величина, принимающая в результате эксперимента какое то значение из некоторой их совокупности и неизвестное заранее, какое именно
О каком событии идет речь? "…Если при одном и том же комплексе условий событие может произойти или не произойти"
(1) достоверное
(2) случайное
(3) невозможное
Два стрелка стреляют по мишени. Вероятность попадания первого стрелка 0,4, второго 0,7. Найти вероятность того, что хотя бы один стрелок попадет в мишень. Ответ введите с точностью до 2-го знака после запятой
0,82
В комнате находятся 15 человек. Необходимо выбрать 4 человека. Сколько разных групп можно составить? Ответ введите с точностью до целых
1365
У пациента измеряли температуру 5 дней по 3 раза – утром, днем и вечером. Получили следующие значения: 37,5; 37,0; 37,9; 37,2; 37,2; 36,8; 36,7; 37,2; 36,8; 36,7; 36,9; 36,7; 36,5; 36,8; 36,7. Что надо сделать, чтобы было удобно работать с данными?
(1) округлить
(2) расположить по возрастанию
(3) расположить по убыванию
(4) расположили полученные значения по возрастанию и подсчитали количество появления каждого из значений
Укажите несовместное событие
(1) получить за один экзамен удовлетворительно и хорошо
(2) повышение температуры днем и появление ветра
(3) встреча знакомого во время прогулки и начало дождя
(4) возникновение лесного пожара и сильный ветер
Два стрелка стреляют по мишени. Вероятность попадания первого стрелка 0,4, второго 0,7. Найти вероятность того, что ни один стрелок не попадет в мишень. Ответ введите с точностью до 2-го знака после запятой
0,18
В комнате находятся 15 человек, из которых 7 девушки. Случайным образом выбирают группу из 4 человек. Сколько в среднем девушек будет в группе? Ответ введите с точностью до целых.
2
Что характеризует математическое ожидание?
(1) вероятность появления некоторой случайной величины
(2) положение случайной величины на числовой оси
(3) наиболее вероятное значение случайной величины
(4) наиболее часто встречающееся значение случайной величины
Имеем 2 события А и В. Определите, в каком примере идет речь о полной группе событий
(1) стрелок стреляет по мишени. А – он попадает в мишень, В – он промахивается
(2) два стрелка одновременно стреляют по мишени А - попадает первый стрелок, В – попадает второй стрелок
(3) игрок кидает кость. А – выпадет 3, В – не выпадет 3
(4) игрок кидает кость. А – выпадет 3, В – выпадет 5
Какая из приведенных формул называется формулой полной вероятности?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Стрелок пристреливал оружие. Он попадает с такого оружия с вероятностью 0,6. Сколько надо сделать выстрелов, чтобы мишень была поражена 5 раз? Ответ введите с точностью до 1-го знака после запятой
8,9
Какие характеристики характеризуют изменчивость случайной величины?
(1) дисперсия
(2) дисперсия, среднеквадратическое отклонение
(3) дисперсия, среднеквадратическое отклонение, коэффициент вариации
(4) Мода, дисперсия, коэффициент вариации
Бросают игральный кубик, на гранях которого числа от 1 до 6. Чему равна вероятность, что выпадет число меньше 6? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
5/6
Один из членов экспедиции никогда не держал ружья в руках и очень стеснялся в этом признаться. Сколько он должен взять с собой патронов, чтобы с вероятностью не менее 0,9 попасть в дичь хотя бы один раз? Принять вероятность поражения цели при одном выстреле 0,01. Ответ введите с точностью до целых
450
В ящике лежит 50 открыток, из которых 30 поздравительных. Не выбирая из ящика берут 10 открыток. Сколько поздравительных открыток будет среди этих 10? Ответ введите с точностью целых
6
В ящике лежат 10 синих, 5 красных и 15 желтых шаров. Вытаскивают 2 шара (по одному). Чему равно вероятность, что эти шары будут одного цвета? Ответ введите с точностью до 2-го знака после запятой
0,37
Игральную кость подбрасывают 6 раз. Какова вероятность выпадения единицы 6 раз? Ответ введите с точностью до 5-го знака после запятой
0,00002
При каждом выстреле из пристреленного оружия вероятность поражения цели равна 0,8. Найти вероятность того, что цель будет поражена 2 раза при 5 выстрелах. Ответ введите с точностью до 3-го знака после запятой
0,512
Если закон распределения случайной величины изображать графически, то по осям координат будут откладываться…. Закончите фразу
(1) по оси ординат откладывать количество значений данной случайной величины, по оси абсцисс – сами значения случайной величины
(2) по оси ординат откладывать вероятности ![math]() , по оси абсцисс – сами значения случайной величины
, по оси абсцисс – сами значения случайной величины
 , по оси абсцисс – сами значения случайной величины
, по оси абсцисс – сами значения случайной величины
(3) по оси ординат откладывать порядковый номер случайной величины, по оси абсцисс – сами значения случайной величины
(4) по оси ординат откладывать значения функции распределения случайной величины, по оси абсцисс – сами значения случайной величины
Найти вероятность извлечь из колоды карт (36 карт) любого короля. Ответ введите в виде несократимой дроби, например 3/5 или 21/23
1/9
В ящике 20 открыток с пейзажем и 6 поздравительных. Из ящика вынимают 2 открытки подряд. Найти вероятность того, что обе открытки будут поздравительные. Ответ введите с точностью до 3-го знака после запятой
0,046
30 % изделий предприятия - изделия из яшмы. Некто приобрел 6 изделий. Чему равна вероятность того, что 4 из них окажутся из яшмы? Ответ введите с точностью до 2-го знака после запятой
0,06
Отметьте виды распределений случайной величины
(1) равномерное
(2) дискретное
(3) нормальное
(4) биноминальное
Для оформления отчета были вырезаны пять букв: " О ", " Т ", " Ч ", " Е ", " Т ". Буквы перемешали и разложили наугад в ряд. Какова вероятность того, что слово " отчет " будет написано правильно? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
1/6
Два охотника независимо друг от друга стреляют по одной мишени, причем каждый из них делает по одному выстрелу. Вероятность попадания в мишень для первого охотника 0,8, а для второго - 0,4. После стрельбы в мишени обнаружили одно отверстие. Найти вероятность того, что она принадлежит второму стрелку? Ответ введите с точностью до 2-го знака после запятой
0,14
Что труднее: выиграть у равносильного противника 5 партий из 8 или 24 из 40
(1) одинаково: ![math]()

(2) труднее 5 партий из 8: ![math]()

(3) труднее 24 из 40: ![math]()

(4) одинаково: ![math]()

Каким образом устанавливается, что экспериментальный ряд подчиняется Пуассоновскому закону распределения?
(1) вычисляют математическое ожидание по двум формулам и сравнивают результат. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(2) вычисляют математическое ожидание и среднеквадратичное отклонение. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(3) вычисляют математическое ожидание и находят середину ряда. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(4) вычисляют математическое ожидание и находят наиболее часто встречающееся значение. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
В коробке лежало 5 образцов с месторождения " Майское " и 2 образца с месторождения "Юность ". Образцы пересчитывают и наугад извлекают образец. Затем образец возвращают в коробку, все опять перемешивают и снова извлекают образец. Найти вероятность того, что оба раза образцы будут с месторождения " Юность ". Ответ введите в виде несократимой дроби, например 3/5 или 21/23
4/49
В полевых условиях использовался ламповый радиопередатчик. Надежность (вероятность безотказной работы) радиолампы в течение некоторого времени равна 0,9. Надежность работы остальных радиоустройств - 0,85, а механической части - 0,95. Найти надежность работы приемника. Ответ введите с точностью до 2-го знака после запятой
0,73
В магазин вошло 8 покупателей. Найти вероятность того, что 3 из них совершат покупки, если вероятность совершить покупку для каждого из них одна и та же - 0,3. Ответ введите с точностью до 2-го знака после запятой
0,25
При экспериментальном моделировании условий выращивания кристаллов проведено 400 опытов. Содержание ![math]() было отмечено во всех опытах, причем в 20 опытах эта величина составила 11,2 %, в 10 - 9,5 %, в 22 - 0,6 %, в 48 - 0,3 %, в 80 - 0,001 % , а во всех остальных 0,1 %. Записать закон распределения величины Х и определить среднее содержание
было отмечено во всех опытах, причем в 20 опытах эта величина составила 11,2 %, в 10 - 9,5 %, в 22 - 0,6 %, в 48 - 0,3 %, в 80 - 0,001 % , а во всех остальных 0,1 %. Записать закон распределения величины Х и определить среднее содержание ![math]() в образцах, дисперсию и среднеквадратическое отклонение
в образцах, дисперсию и среднеквадратическое отклонение
 было отмечено во всех опытах, причем в 20 опытах эта величина составила 11,2 %, в 10 - 9,5 %, в 22 - 0,6 %, в 48 - 0,3 %, в 80 - 0,001 % , а во всех остальных 0,1 %. Записать закон распределения величины Х и определить среднее содержание
было отмечено во всех опытах, причем в 20 опытах эта величина составила 11,2 %, в 10 - 9,5 %, в 22 - 0,6 %, в 48 - 0,3 %, в 80 - 0,001 % , а во всех остальных 0,1 %. Записать закон распределения величины Х и определить среднее содержание  в образцах, дисперсию и среднеквадратическое отклонение
в образцах, дисперсию и среднеквадратическое отклонение
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Три охотника попадают в летящую утку с вероятностями, соответственно равными 2/3, 3/4, 1/4. Все трое одновременно стреляют по пролетающей утке. Какова вероятность, что утка будет убита, если для этого достаточно хотя бы одного попадания? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
15/16
По глухарю производятся два выстрела. Вероятность попадания при первом выстреле - 0,5, а при втором - 0,8. Для того чтобы глухаря убить, надо 2 попадания. Найти вероятность того, что после двух выстрелов глухарь будет убит. Ответ введите с точностью до 1-го знака после запятой
0,4
Вероятность вырастить идеальный кристалл кварца равна 1/4. Было установлено 34 153 заготовки. Сколько идеальных кристаллов кварца можно вырастить в этих условиях?
(1) 8403 или 8404
(2) 8522 или 8523
(3) 8538 или 8539
(4) 8622 или 8623
Вероятность сдать заказ в ателье в некотором городе равна ![math]() . Настойчивый клиент обходит имеющиеся в городе ателье, пока не добьется успеха. Какова вероятность, что ему удастся не менее чем с третьего раза сдать заказ, если по статистике среднее число попыток равно 5? Ответ введите с точностью до 2-го знака после запятой
. Настойчивый клиент обходит имеющиеся в городе ателье, пока не добьется успеха. Какова вероятность, что ему удастся не менее чем с третьего раза сдать заказ, если по статистике среднее число попыток равно 5? Ответ введите с точностью до 2-го знака после запятой
 . Настойчивый клиент обходит имеющиеся в городе ателье, пока не добьется успеха. Какова вероятность, что ему удастся не менее чем с третьего раза сдать заказ, если по статистике среднее число попыток равно 5? Ответ введите с точностью до 2-го знака после запятой
. Настойчивый клиент обходит имеющиеся в городе ателье, пока не добьется успеха. Какова вероятность, что ему удастся не менее чем с третьего раза сдать заказ, если по статистике среднее число попыток равно 5? Ответ введите с точностью до 2-го знака после запятой
0,64
Каждая из первых пяти последовательных букв русского алфавита написана на отдельной карточке. Все карточки перемешиваются на столе "вниз лицом". Какова вероятность того, что из выбранных наугад четырех карточек получится слово: "вода"? Ответ введите с точностью до целых
0
По одной и той же мишени производят по одному выстрелу с дистанции 600, 500 и 300 м. Вероятности попадания с этих дистанций соответственно равны 0,1; 0,2 и 0,4. Определить вероятность не менее двух попаданий в мишень. Ответ введите с точностью до 3-го знака после запятой
0,124
Вероятность положительной пробы в каждом из 100 независимых анализов равна 0,8. Найти сколько раз может быть зарегистрирован положительный результат
(1) 79 или 80
(2) 80 или 81
(3) 81 или 82
(4) 83 или 84
Распределения вероятности некоторой случайной величины задана соотношением . Найти функцию распределения, полагая, что здесь мы имеем равномерный закон распределения. Построить полученную функцию

На анализ в химическую лабораторию привезли 1000 образцов. После анализа оказалось, что один образец содержит золото, 10 – серебро, 50 – цинк, 100 – медь, в остальных образцах ничего, заслуживающего внимания, не нашли. Лаборант берет один из образцов на повторный анализ. Какова вероятность того, что в образце будет содержаться цинк или медь? Ответ введите с точностью до 2-го знака после запятой
0,15
При взрывных работах в районе взрыва заряда крупные, средние и мелкие осколки образуются в отношении 1:3:6. Вероятность того, что крупный осколок упадет в небольшую речку, которая протекает в районе взрыва, равна 0,3, средний - 0,9, мелкий - 0,1. Найти вероятность того, что в реку упадет хотя бы один осколок. Ответ введите с точностью до 2-го знака после запятой
0,39
Принимая равновероятным рождение мальчика и девочки, найти, сколько будет новорожденных мальчиков при 4000 новорожденных
(1) 1999 или 2000
(2) 2000 или 2001
(3) 2001 или 2002
(4) 2003 или 2004
Если ![math]() является плотностью распределения некоторой случайной величины на интервале
является плотностью распределения некоторой случайной величины на интервале ![math]() , и 0 для всех остальных
, и 0 для всех остальных ![math]() . Найти
. Найти ![math]()
 является плотностью распределения некоторой случайной величины на интервале
является плотностью распределения некоторой случайной величины на интервале  , и 0 для всех остальных
, и 0 для всех остальных  . Найти
. Найти 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Два охотника стреляют одновременно. Какова вероятность поражения дичи, если один попадает с вероятностью 0,3, а второй – 0,4? Ответ введите с точностью до 2-го знака после запятой
0,58
Три карабина, которые планировалось взять в экспедицию, оказались плохо пристрелянные. Вероятность попадания в цель из первого карабина равна 0,2, а из двух других 0,3. Один человек при контрольной проверке стреляет в мишень и попадает. Найти вероятность того, что для проверки был выбран первый карабин. (Проверяющий стреляет со 100% попаданием.) Ответ введите с точностью до 2-го знака после запятой
0,25
На тренировке спортсмен кидает копья, которые летят вдоль оси Х. Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит 1/2 расстояния средней дальности. Ответ введите с точностью до 5-го знака после запятой
0,00065
В выработке для передвижения по горизонтам использовали небольшие поезда, состоящие из 3 вагончиков по 6 мест в каждом. 9 шахтеров рассаживаются в таком поезде. Какова вероятность того, что в каждый вагон сядут по 3 человека? Ответ введите с точностью до 2-го знака после запятой
0,03
Масса кристаллов кварца, найденных туристами, распределилась следующим образом: 3 кристалла весили 14 г, четыре 18 г, два 23 г, один 32 г. Считая массу кристалла случайной величиной, построить закон распределения (функция плотности вероятностей) этой величины
(1)
(2)
(3)
(4)
Карта некоторой местности разбита на квадраты со стороной ![math]() . На карту падает монета диаметром
. На карту падает монета диаметром ![math]() . Какова вероятность, что монета не пересечет ни одну из сторон квадратов?
. Какова вероятность, что монета не пересечет ни одну из сторон квадратов?
 . На карту падает монета диаметром
. На карту падает монета диаметром  . Какова вероятность, что монета не пересечет ни одну из сторон квадратов?
. Какова вероятность, что монета не пересечет ни одну из сторон квадратов?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Группа студентов из 24 человек после экзамена получила следующие оценки: половина всей группы сдала на "хорошо" и "отлично"; треть получили: "удовлетворительно", а остальные "неудовлетворительно". Построить закон распределения полученных оценок
| 12 | 8 | 4 |
| 4,5 | 3 | 2 |
| 0,5 | 0,3 | 0,2 |
| 12 | 8 | 4 |
| 4 | 3 | 2 |
| 0,5 | 0,3 | 0,2 |
| 12 | 8 | 4 |
| 5 | 3 | 2 |
| 0,5 | 0,3 | 0,2 |
| 12 | 8 | 4 |
| 4,5 | 3 | 2 |
| 0,5 | 0,33 | 0,17 |
(1) правильные таблица 1
(2) правильные: таблица 2 и 3
(3) правильные: все таблицы
(4) правильные таблицы 1 и 4
В квадрат вписан круг. Какова вероятность того, что точка, брошенная наудачу в квадрат, окажется внутри круга?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Рассчитать среднее, дисперсию и среднеквадратическое отклонение.
| 76,87 | 57,58 | 59,76 | 80,87 | 68,60 | 43,20 | 76,85 | 71,01 | 75,61 | 37,87 | 42,97 |
| 60,73 | 48,37 | 68,71 | 68,85 | 65,68 | 60,06 | 42,28 | 73,72 | 63,21 | 69,40 | 67,40 |
| 36,90 | 60,47 | 45,96 | 91,36 | 80,21 | 72,83 | 72,25 | 72,90 | 43,15 | 86,75 | 63,62 |
| 76,63 | 65,56 | 65,56 | 62,68 | 61,72 | 76,71 | 85,73 | 71,87 | 57,58 |
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие события могут быть признаны случайными?
(1) количество людей на автобусной остановке
(2) количество мест для пассажиров в поезде
(3) число машин на автостоянке
(4) количество образцов с положительной реакцией в общем объеме образцов
Отметьте правильно написанную формулу:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Подсчитайте результат ![math]() . Ответ введите с точностью до целых
. Ответ введите с точностью до целых
 . Ответ введите с точностью до целых
. Ответ введите с точностью до целых
126
Какие основные типы случайной величины встречаются исследователю?
(1) дискретная
(2) непрерывная
(3) выборочная
(4) детерминированная
О каком событие идет речь? "…при одном и том же комплексе условий обязательно произойдет"
(1) достоверное
(2) случайное
(3) невозможное
Два стрелка стреляют по мишени. Вероятность попадания первого стрелка 0,4, второго 0,7. Найти вероятность того, что только один стрелок попадет в мишень. Ответ введите с точностью до 2-го знака после запятой
0,54
В комнате находятся 15 человек, из которых 7 девушки. Необходимо выбрать 4 человека. Какова вероятность, что будут выбраны только девушки? Ответ введите с точностью до 2-го знака после запятой
0,03
Исследователь расположил полученные данные по возрастанию. Как называется это действие?
(1) упорядочивание
(2) ранжирование
(3) варьирование
(4) оценивание
Имеем 2 события А и В. Определите, в каком примере можно использовать сумму событий
(1) игрок кидает кость. А – выпадет 3, В – выпадет 5
(2) игрок кидает 2 кости. А – выпадет 3, В – выпадет 5
(3) стрелок стреляет по мишени. А – он попадает в мишень, В – он промахивается
(4) два стрелка одновременно стреляют по мишени А - попадает первый стрелок, В – попадает второй стрелок
(5) один стрелок стреляет 2 раза по мишени. А – он попадает в мишень, В – он промахивается
В ящике лежат по 10 белых, красных и синих шаров. Из ящика извлекают сначала один шар, потом другой. Найти вероятность, что среди шаров не будет синих. Ответ введите с точностью до 2-го знака после запятой
0,89
Стрелок пристреливал оружие. Он попадает с такого оружия с вероятностью 0,6. Стрелок сделал 15 выстрелов. Найти вероятность, что мишень была поражена 7 раз. Ответ введите с точностью до 2-го знака после запятой
0,12
В каком случае выполняется равенство ![math]() ?
?
 ?
?
(1) если случайная величина независима
(2) если случайная величина дискретна
(3) если случайная величина представлена вариационным рядом
(4) если случайная величина зависима
Бросают монетку. Какова вероятность того, что выпадет решка? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
1/2
Бросают две игральные кости. Какова вероятность того, что сумма выпавших очков будет: кратна 3? Ответ введите с точностью до 2-го знака после запятой
0,33
В ящике лежит 50 открыток, из которых 30 поздравительных. К сожалению, свет в комнате не горит, а надо срочно подписать поздравительную открытку. Какое минимальное количество открыток надо взять наугад, чтобы среди них оказалась 1 поздравительная с вероятностью не менее 1/2?
(1) 5
(2) 1
(3) 3
(4) 2
Одна группа рабочих, 10 человек, на изготовление 1 детали затрачивают по 6 мин; вторая группа рабочих, 10 чел., на изготовление 1 детали затрачивают по 12 мин., а группа учеников – 18 мин. Все группы объединили. Определить среднее время, не¬об¬ходимое для изготовления одной детали, при котором за 1 час работы все¬ми рабочими изготовилось бы такое же количество деталей
(1) 12 мин
(2) 9,5 мин
(3) 10,2
(4) 8 мин
Два стрелка стреляют по мишени. Вероятность попадания первого стрелка 0,6, второго 0,7. Найти вероятность того, что оба стрелка попадут в мишень. Ответ введите с точностью до 2-го знака после запятой
0,42
Подбрасывают 2 монеты. Какова вероятность того, что на обеих выпадет герб ? Ответ введите с точностью до 2-го знака после запятой
0,25
Если ![math]() и
и ![math]() не целые числа, то для того, чтобы определить
не целые числа, то для того, чтобы определить ![math]() - наивероятнейшее число появления события
- наивероятнейшее число появления события ![math]() при
при ![math]() испытаниях, эти числа… продолжите фразу
испытаниях, эти числа… продолжите фразу
 и
и  не целые числа, то для того, чтобы определить
не целые числа, то для того, чтобы определить  - наивероятнейшее число появления события
- наивероятнейшее число появления события  при
при  испытаниях, эти числа… продолжите фразу
испытаниях, эти числа… продолжите фразу
(1) округляются до ближайшего целого, но так, чтобы интервал не увеличивался
(2) округляются до ближайшего целого
(3) округляются до ближайшего целого, но так, чтобы эти числа попали в интервал округления
Дайте определение независимых случайных величин
(1) случайные величины называются независимыми, если появление одной не зависит от появления другой
(2) случайные величины называются независимыми, если закон распределения одной не зависит от закона распределения другой
(3) случайные величины называются независимыми, если закон распределения одной исключает построение закона распределения другой
(4) случайные величины называются независимыми, если они принадлежат разным выборкам
Штаб неприятеля – дом с прямоугольным с основанием , размером 40х100 м. Его месторасположение неизвестно. Известно только, что он находится в квадрате со стороной 1000 м. Если бомбардировать этот квадрат случайно, найти вероятность попадания в штаб. Ответ введите с точностью до 4-го знака после запятой
0,0004
Игральную кость подбрасывают 6 раз. Какова вероятность выпадения 3 раза одинаковых граней? Ответ введите с точностью до 2-го знака после запятой
0,16
Связь с шестью дальними партиями была организована через радио посредством радиостанций. Каждая партия в течение дня могла в любое время связаться с базой, где радиостанция работала круглосуточно. Если вероятность связи с любой партией 0,8, найти вероятность того, что в данный момент все партии вышли на связь. Ответ введите с точностью до 5-го знака после запятой
0,26214
Выберите правильные утверждения
(1) Функция распределения есть не отрицательная функция, значение которой изменяются от 0 до 1: ![math]()

(2) вероятность попадания случайной величины в некоторый интервал ![math]() равно разности значений функций распределений на концах этого интервала
равно разности значений функций распределений на концах этого интервала ![math]()
 равно разности значений функций распределений на концах этого интервала
равно разности значений функций распределений на концах этого интервала 
(3) вероятность попадания непрерывной случайной величины в неконкретный интервал равна ![math]()

(4) значение функции распределения на ![math]() равно нулю
равно нулю
 равно нулю
равно нулю Для оформления отчета были вырезаны пять букв: " О ", " Т ", " Ч ", " Е ", " Т ". Буквы перемешали и разложили наугад в ряд и стали вытаскивать наугад по одной. Какова вероятность того, что получится слово " чет ". Ответ введите в виде несократимой дроби, например 3/5 или 21/23
1/30
Производится три выстрела из одного и того же оружия по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,4; 0,5 и 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна пробоина. Ответ введите с точностью до 2-го знака после запятой
0,91
Задача 1. Производится 19 бросков в цель. Вероятность попадания в цель, при каждом броске, равна 0,8. Найти наивероятнейшее количество попаданий в цель
(1) 14 или 15
(2) 15 или 16
(3) 16 или 17
(4) 17 или 18
Из 10 образцов, исследованных в лаборатории, 4 имели плотность ![math]() и остальные
и остальные ![math]() . Считая измерения независимыми, найти среднюю плотность образцов. Ответ введите с точностью до 2-го знака после запятой
. Считая измерения независимыми, найти среднюю плотность образцов. Ответ введите с точностью до 2-го знака после запятой
 и остальные
и остальные  . Считая измерения независимыми, найти среднюю плотность образцов. Ответ введите с точностью до 2-го знака после запятой
. Считая измерения независимыми, найти среднюю плотность образцов. Ответ введите с точностью до 2-го знака после запятой
2,57
В коробке лежало 5 образцов с месторождения " Майское " и 2 образца с месторождения " Юность ". Образцы перемешивают и наугад извлекают образец. Затем образец возвращают в коробку, все опять перемешивают и снова извлекают образец. Найти вероятность того, что образцы будут с разных месторождений. Ответ введите в виде несократимой дроби, например 3/5 или 21/23
20/49
На 3 местa водителя претендуют 3 человека. После анализа и сопоставления документов оказалось, что вероятности приема на работу первого, вто¬рого и третьего претендентов соответственно равны 0,8; 0,7; 0,6. Найти вероятность того, что хотя бы одному из претендентов не откажут. Ответ введите с точностью до 2-го знака после запятой
0,98
В трехместном номере гостиницы над каждой из кроватей находится светильник. Вероятность того, что светильник включен для каждого из них, будет равна 0,6. Найти вероятность того, что в данный момент включен хотя бы один светильник. Ответ введите с точностью до 3-го знака после запятой
0,936
При изучении упругих свойств образцов материалов получили следующие значения скоростей распространения упругих волн: 5,66; 5,86; 5,66; 5,76; 5,82; 5,54; 6,12; 5,54; 6,12; 5,82; 6,28; 5,94. Среднее значение ![math]() в этому виду материалов равно 5,80. Вычислить среднее, дисперсию и среднеквадратическое отклонение. Сравнить отклонение экспериментального среднего от среднего по породе
в этому виду материалов равно 5,80. Вычислить среднее, дисперсию и среднеквадратическое отклонение. Сравнить отклонение экспериментального среднего от среднего по породе
 в этому виду материалов равно 5,80. Вычислить среднее, дисперсию и среднеквадратическое отклонение. Сравнить отклонение экспериментального среднего от среднего по породе
в этому виду материалов равно 5,80. Вычислить среднее, дисперсию и среднеквадратическое отклонение. Сравнить отклонение экспериментального среднего от среднего по породе
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для поражения цели (заяц) достаточно хотя бы одного попадания. Производятся два выстрела одновременно. Найти вероятность поражения цели, если вероятность попадания в цель первым охотником равна 0,3, а вторым - 0,4? Ответ введите с точностью до 2-го знака после запятой
0,58
Охотник выстрелил 3 раза по улетающей от него утке. Причем если вероятность попадания в утку при первом выстреле у охотника была 0,7, то после каждого выстрела она уменьшалась на 0,1. Вычислить вероятность попасть в утку хотя бы один раз. Ответ введите с точностью до 2-го знака после запятой
0,94
некто, не умеющий стрелять, произвел 14 выстрелов, пытаясь сбить банку с пенька. Вероятность попадания в банку равна 0,2. Найти наивероятнейшее число попаданий
(1) ни одного
(2) 1 или 2
(3) 2 или 3
(4) 3 или 4
Приемщица за 1 час принимает 2 заявки от клиентов. Предполагается простейший поток заявок (распределение Пуассона). Чему равна вероятность поступления четырех заявок за 4 часа? Ответ введите с точностью до 4-го знака после запятой
0,0058
После проверки оружия в барабане револьвера осталось 2 патрона. Остальные гильзы были пустыми (всего мест в барабане 7). Ночью на геологов напал медведь. В него попытались выстрелить два раза. Какова вероятность того, что выстрелы прозвучали хотя бы один раз? Ответ введите с точностью до 1-го знака после запятой
0,5
Три человека сидят в креслах и смотрят телевизор. Недалеко от них коробка для разного мелкого мусора. Все трое съели по конфете, а бумажки, скомкав, бросили, не вставая, в коробку для мелкого мусора. Какова вероятность того, что только один из них попадет в коробку, если вероятности попадания бумажкой для каждого из них соответственно равны 0,9; 0,8 и 0,7? Ответ введите с точностью до 2-го знака после запятой
0,09
Статистикой установлено, что из каждой 1000 родившихся детей в среднем рождается 485 де¬вочек, а остальные - мальчики. В семье 5 детей. Найти вероятность того, что среди этих детей 3 девочки. Ответ введите с точностью до 2-го знака после запятой
0,14
Случайная непрерывная величина ![math]() задана функцией распределения . Требуется найти плотность распределения
задана функцией распределения . Требуется найти плотность распределения ![math]() и построить графики функций
и построить графики функций ![math]() и
и ![math]()
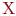 задана функцией распределения . Требуется найти плотность распределения
задана функцией распределения . Требуется найти плотность распределения  и построить графики функций
и построить графики функций  и
и 

При выполнении взрывных работ используют три вида зарядов. Вероятность самопроизвольного взрыва первого вида заряда 0,01, второго 0,025 и третьего 0,008. При взрыве любого заряда детонируют остальные. Найти вероятность самопроизвольного взрыва. Ответ введите с точностью до 2-го знака после запятой
0,04
При передаче сообщений азбукой Морзе сигналы "точка" - "тире" встречаются в отношении 5:3. Статистические свойства помех таковы, что искажаются в среднем 2/5 сообщения "точка" и 1/3 сообщений "тире". Найти вероятность того, что произвольный сигнал из принятых не искажен. Ответ введите с точностью до 3-го знака после запятой
0,542
Вероятность появления события в каждом из 10 000 независимых испытаний равна 3/4. Найти вероятность того, что относительная частота появления события отклоняется от его вероятности по абсолютной величине не более чем на 0,01. Ответ введите с точностью до 2-го знака после запятой
0,81
Случайная величина ![math]() подчинена закону распределения с плотностью вероятностей . Требуется найти коэффициент
подчинена закону распределения с плотностью вероятностей . Требуется найти коэффициент ![math]()
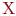 подчинена закону распределения с плотностью вероятностей . Требуется найти коэффициент
подчинена закону распределения с плотностью вероятностей . Требуется найти коэффициент 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В группе студентов-практикантов было 17 юношей и 8 девушек. Какова вероятность того, что студент, фамилия которого будет названа первым, будет девушкой? Ответ введите с точностью до 2-го знака после запятой
0,32
Приборы, полученные в геологическом управлении, для использования в новом полевом сезоне были на 70 % от отечественных производителей, а остальные - импортные. Для отечественных приборов надежность (вероятность безотказной работы) в течение одного полевого сезона составила 0,95, а у импортных - 0,92. Некоторый прибор в течение всего полевого сезона работал безотказно. Найти вероятность того, что это был отечественный прибор. Ответ введите с точностью до 1-го знака после запятой
0,7
На тренировке спортсмен кидает копья, которые летят вдоль оси Х. Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит расстояние больше 1/2 средней дальности. Ответ введите с точностью до 5-го знака после запятой
0,49993
В выработке для передвижения по горизонтам использовали небольшие поезда, состоящие из 3 вагончиков по 6 мест в каждом. 9 шахтеров рассаживаются в таком поезде. Какова вероятность того, что хотя бы в один из вагонов сядут четверо? Ответ введите с точностью до 3-го знака после запятой
0,008
Масса кристаллов кварца, найденных туристами, распределилась следующим образом: 3 кристалла весили 14 г, четыре 18 г, два 23 г, один 32 г. Считая массу кристалла случайной величиной, найти математическое ожидание, дисперсию и среднеквадратическое отклонение измеренной величины
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Территория склада имеет форму прямоугольника со сторонами 50 м и 30 м. На этой территории находится 4 больших бака с ГСМ диаметром 10 м каждый. Во время грозы на территорию склада ударила молния. Найти вероятность попадания молнии в любой бак с ГСМ, если попадание молнии в любую точку территории склада равновероятно? Ответ введите с точностью до 2-го знака после запятой
0,21
Группа студентов из 24 человек после экзамена получила следующие оценки: половина всей группы сдала на "хорошо" и "отлично"; треть получили: "удовлетворительно", а остальные "неудовлетворительно". Найти среднее, дисперсию и среднеквадратическое отклонение
(1) ![math]()

(2) ![math]()

(3) ![math]()

Маршруты двух групп туристов были составлены так, что они около водопада должны быть в один день и тот же день. Если первая группа провела у водопада 1 час, а вторая группа - 2 часа, найти вероятность того, что обе группы встретятся. Ответ введите с точностью до 2-го знака после запятой
0,12
Перейти к интервальному ряду, построить гистограмму частот. Указание.  выбрать равным 6
выбрать равным 6
| 0,30 | 0,38 | 0,50 | 1,75 | 0,12 | 0,10 | 0,54 | 0,35 | 0,30 | 0,10 | 3,64 |
| 1,20 | 0,34 | 0,19 | 0,72 | 0,05 | 0,31 | 4,13 | 0,27 | 3,06 | 0,11 | 0,40 |
| 2,46 | 0,13 | 4,10 | 0,22 | 1,81 | 1,13 | 0,80 | 1,08 | 0,16 | 4,05 | 0,46 |
| 3,98 | 1,22 | 0,69 | 0,12 | 0,19 | 1,63 | 2,19 | 4,41 | 3,80 | 0,53 | 1,75 |
| 0,50 | 1,59 | 3,64 | 0,92 | 4,14 | 0,18 | 3,64 | 1,26 | 0,33 | 1,50 | 0,55 |
| 2,02 |
| интервалы | частоты |
|---|---|
| 0 | 0 |
| 0,727 | 0,518 |
| 1,453 | 0,125 |
| 2,18 | 0,125 |
| 2,907 | 0,036 |
| 3,633 | 0,018 |
| 4,36 | 0,161 |
| 5,087 | 0,018 |
| интервалы | частоты |
|---|---|
| 0,872 | 0,536 |
| 1,744 | 0,161 |
| 2,616 | 0,107 |
| 3,488 | 0,018 |
| 4,360 | 0,161 |
| 5,232 | 0,018 |
| 6,104 | 0,000 |
| интервалы | частоты |
|---|---|
| 0,000 | 0,000 |
| 0,727 | 0,518 |
| 1,453 | 0,125 |
| 2,180 | 0,125 |
| 2,907 | 0,036 |
| 3,633 | 0,018 |
| 4,360 | 0,161 |
| интервалы | частоты |
|---|---|
| 0,000 | 0,000 |
| 0,872 | 0,536 |
| 1,744 | 0,161 |
| 2,616 | 0,107 |
| 3,488 | 0,018 |
| 4,360 | 0,161 |
| 5,232 | 0,018 |


(1) таблица 3, диаграмма 1
(2) таблица 2, диаграмма 2
(3) таблица 1, диаграмма 1
(4) таблица 4, диаграмма 2
Группа студентов, направленных на летнюю практику в одно геологическое управление, состояла из 7 студентов специальности "Открытые горные работы", 9 - "Маркшейдер", 2 - "Геология". Какова вероятность, что первые три студента, зашедшие в кабинет руководителя практики, окажутся студентами, обучающимися по специальности "Маркшейдер"? Ответ введите с точностью до 1-го знака после запятой
0,1
По шапке, закинутой на дерево, производится 6 выстрелов, причем, чтобы шапка упала, необходимо 2 попадания. Найти вероятность того, что шапка упадет вниз, если вероятность попадания при каждом выстреле равна 0,2. Ответ введите с точностью до 2-го знака после запятой
0,35
Для каких целей часто экспериментальные данные логарифмируют?
(1) чтобы избавиться от больших значений
(2) чтобы уменьшить разброс данных
(3) для того, чтобы данные сравнить с нормальным распределением. Это один из шагов стандартизации данных
(4) для того, чтобы проверить тип распределения
Назовите дисциплины, которые являются теоретической базой вероятностно-статистического метода
(1) математический анализ
(2) теория вероятностей
(3) теория групп
(4) математическая статистика
В ящике 12 открыток. Случайным образом выбирают 3 открытки. Сколькими способами можно это сделать? Ответ введите с точностью до целых
220
Случайной величиной называется такая, которая может принимать конечное или бесконечное счетное множество значений… О какой случайной величине идет речь?
(1) дискретная
(2) непрерывная
(3) выборочная
(4) детерминированная
О каком событие идет речь? "…которое заведомо не может произойти при любом комплексе условий эксперимента"
(1) достоверное
(2) случайное
(3) невозможное
В комнате находятся 15 человек, из которых 7 девушки. Необходимо выбрать 4 человека. Какова вероятность, что будут выбраны только девушки? Определите формулу, по которой можно найти ответ на заданный вопрос.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Что называется варьированием?
(1) распределение данных по возрастанию
(2) наблюдаемое значение некоторого признака случайной величины
(3) составление ряда из вариант
(4) изменение некоторого признака случайной величины
Имеем 2 события А и В. Определите, в каком примере можно использовать произведение событий
(1) игрок кидает кость. А – выпадет 3, В – выпадет 5
(2) игрок кидает 2 кости. А – выпадет 3, В – выпадет 5
(3) стрелок стреляет по мишени. А – он попадает в мишень, В – он промахивается
(4) два стрелка одновременно стреляют по мишени А - попадает первый стрелок, В – попадает второй стрелок
(5) один стрелок стреляет 2 раза по мишени. А – он попадает в мишень, В – он промахивается
Какая из приведенных формул называется формула Байеса?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Стрелок пристреливал оружие. Он попадает с такого оружия с вероятностью 0,6. Стрелок сделал 15 выстрелов. Найти наивероятнейшее число попаданий в мишень. Ответ введите с точностью до целых
9
Определите понятие моды
(1) это такое значение ![math]() , для которого
, для которого ![math]() наибольшее
наибольшее
 , для которого
, для которого  наибольшее
наибольшее
(2) это такое значение ![math]() , ко¬торое находится в центре ранжированного ряда
, ко¬торое находится в центре ранжированного ряда
 , ко¬торое находится в центре ранжированного ряда
, ко¬торое находится в центре ранжированного ряда
(3) это такое значение ![math]() , для которого
, для которого ![math]() наибольшее. Если таких значений несколько, то мода не определяется
наибольшее. Если таких значений несколько, то мода не определяется
 , для которого
, для которого  наибольшее. Если таких значений несколько, то мода не определяется
наибольшее. Если таких значений несколько, то мода не определяется
(4) это такое значение ![math]() , которое находится в центре ранжированного ряда, если длина ряда выражена нечетным числом
, которое находится в центре ранжированного ряда, если длина ряда выражена нечетным числом
 , которое находится в центре ранжированного ряда, если длина ряда выражена нечетным числом
, которое находится в центре ранжированного ряда, если длина ряда выражена нечетным числом В ящике 15 открыток, среди которых только 6 с цветами. Взяли 1 открытку. Какова вероятность того, что на открытке будут цветы? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
2/5
Один охотник пошел на охоту, но стрелял он очень плохо. Сколько ему следует взять с собой патронов, чтобы с вероятностью не менее 0,5 попасть в дичь хотя бы один раз? Принять вероятность поражения цели при одном выстреле 0,01. Ответ введите с точностью до целых
392
В ящике лежит 50 открыток, из которых 30 поздравительных. Не выбирая из ящика берут 20 открыток. Сколько не поздравительных открыток будет среди этих 20? Ответ введите с точностью до целых
8
На участке дороги есть 4 населенных пункта ![math]() ,
, ![math]() ,
, ![math]() и
и ![math]() , в которых проживает 80, 20, 40 и 100 жителей, соответственно. Расстояние от города А0 до указанных населенных пунктов составляет 2, 10, 15 и 16 км. Для удобства жителей организуют автобусный маршрут до го¬ро¬да. Определить, в каком из населенных пунктов следует сделать ав¬то¬бус¬ную останов¬ку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
, в которых проживает 80, 20, 40 и 100 жителей, соответственно. Расстояние от города А0 до указанных населенных пунктов составляет 2, 10, 15 и 16 км. Для удобства жителей организуют автобусный маршрут до го¬ро¬да. Определить, в каком из населенных пунктов следует сделать ав¬то¬бус¬ную останов¬ку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
 ,
,  ,
,  и
и  , в которых проживает 80, 20, 40 и 100 жителей, соответственно. Расстояние от города А0 до указанных населенных пунктов составляет 2, 10, 15 и 16 км. Для удобства жителей организуют автобусный маршрут до го¬ро¬да. Определить, в каком из населенных пунктов следует сделать ав¬то¬бус¬ную останов¬ку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
, в которых проживает 80, 20, 40 и 100 жителей, соответственно. Расстояние от города А0 до указанных населенных пунктов составляет 2, 10, 15 и 16 км. Для удобства жителей организуют автобусный маршрут до го¬ро¬да. Определить, в каком из населенных пунктов следует сделать ав¬то¬бус¬ную останов¬ку, чтобы общий путь пассажиров до автобусной остановки был бы наименьшим ?
(1) во втором пункте
(2) в третьем пункте
(3) между вторым и третьим пунктом
(4) пассажиров первого пункта можно не учитывать, т.к. поселок близко от города. Тогда между вторым и третьим пунктом
В ящике лежат 10 синих, 5 красных и 15 желтых шаров. Вытаскивают 2 шара одновременно. Чему равно вероятность, что эти шары будут одного цвета? Ответ введите в виде несократимой дроби, например 3/5 или 21/23
11/15
Брошены 2 игральные кости. Какова вероятность выпадения двух различных граней? Ответ введите с точностью до 2-го знака после запятой
0,83
Задача 1. Вероятность того, что в один из дней не будет перерасхода горючего для вездехода, равна 3/4. Какова вероятность того, что лишь в один из 6 полевых дней не будет перерасхода горючего? Ответ введите с точностью до 4-го знака после запятой
0,0044
Случайная величина может принимать значения ![math]() . О каком типе случайной величины идет речь?
. О каком типе случайной величины идет речь?
 . О каком типе случайной величины идет речь?
. О каком типе случайной величины идет речь?
(1) независимой
(2) зависимой
(3) дискретной
(4) непрерывной
Найти вероятность извлечь из колоды карт карту красной масти. Ответ введите в виде несократимой дроби, например 3/5 или 21/23
1/2
Чему равна вероятность того, что при бросании трех игральных костей 6 очков появятся хотя бы один раз? Кости брошены только один раз. Ответ введите с точностью до 2-го знака после запятой
0,42
Связь с шестью дальними партиями была организована через радио посредством радиостанций. Каждая партия в течение дня могла в любое время связаться с базой, где радиостанция работала круглосуточно. Если вероятность связи с любой партией 0,8, найти вероятность того, что в данный момент никто не вышел на связь. Ответ введите с точностью до 6-го знака после запятой
0,000064
Выберите, что не является свойством функции плотности распределения ![math]()

(1) эта функция является интегральной характеристикой функции распределения
(2) площадь под кривой плотности распределения на всей ее области определения равна единице ![math]()

(3) функция плотности распределения ![math]() существует везде, за исключением, может быть, конечного числа точек
существует везде, за исключением, может быть, конечного числа точек
 существует везде, за исключением, может быть, конечного числа точек
существует везде, за исключением, может быть, конечного числа точек
(4) дифференциальная функция распределения ![math]() не отрицательна для любого
не отрицательна для любого ![math]() из ее области определения
из ее области определения ![math]()
 не отрицательна для любого
не отрицательна для любого  из ее области определения
из ее области определения 
(5) интегральная функция распределения случайной вели¬чи¬ны может быть выражена через функцию плотности вероятностей по формуле ![math]()

Компания из ![math]() человек садится за круглый стол в случайном порядке. С какой вероятностью два определенных лица будут сидеть рядом?
человек садится за круглый стол в случайном порядке. С какой вероятностью два определенных лица будут сидеть рядом?
 человек садится за круглый стол в случайном порядке. С какой вероятностью два определенных лица будут сидеть рядом?
человек садится за круглый стол в случайном порядке. С какой вероятностью два определенных лица будут сидеть рядом?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вероятность того, что студент сдает первый экзамен на "отлично" равна 0,9, второй - 0,9, третий - 0,8. Вычислить вероятность того, что студент сдаст не менее двух экзаменов на "отлично". Ответ введите с точностью до 3-го знака после запятой
0,954
Каждый участник геологического конгресса в свободный от заседаний день может с вероятностью 1/3 либо осматривать город, либо вернуться в гостиницу, либо участвовать в дискуссиях, обсуждая прошедшие заседания. Найти вероятность того, что из 203 участников конгресса 71 отправятся осматривать город. Ответ введите с точностью до 3-го знака после запятой
0,052
Каким образом определить, что экспериментальные данные распределены равномерно?
(1) вычисляют математическое ожидание по двум формулам и сравнивают результат. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(2) вычисляют математическое ожидание и дисперсию данных. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(3) вычисляют математическое ожидание и находят середину ряда. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
(4) вычисляют математическое ожидание и находят наиболее часто встречающееся значение. Оба полученных значения сравнивают между собой. Если оба значения разнятся меньше, чем на 10%, то делают вывод о равномерном распределении
В коробке лежало 5 образцов с месторождения " Майское " и 2 образца с месторождения "Юность ". Образцы пересчитывают и наугад извлекают образец. Затем образец возвращают в коробку, все опять перемешивают и снова извлекают образец. Найти вероятность того, что оба раза образцы будут с месторождения " Майское ". Ответ введите в виде несократимой дроби, например 3/5 или 21/23
25/49
В ящике 2 красных шара и 6 синих шаров. Шары отличаются только цветом. Для пробы из ящика берут один шар, а затем его возвращают обратно. Далее снова берут один шар. Найти вероятность того, что оба раза были извлечены красные шары. Ответ введите с точностью до 4-го знака после запятой
0,0625
Лаборант, сортируя образцы, бракованные бросает в недалеко стоящий ящик. Вероятность того, что он не промахнется, равна 0,8. Найти вероятность того, что из 100 брошенных образцов 75 окажутся в ящике. Ответ введите с точностью до 3-го знака после запятой
0,046
При испытании соединения на прочность при воздействие ударной нагрузки по пре¬дельной схеме были получены следующие результаты: ![math]() . Определить среднее, дисперсию и среднеквадратическое отклонение
. Определить среднее, дисперсию и среднеквадратическое отклонение
 . Определить среднее, дисперсию и среднеквадратическое отклонение
. Определить среднее, дисперсию и среднеквадратическое отклонение
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

На участке пробурили 1000 скважин. В одной скважине было определено повышенное содержание золота, в 10 скважинах - марганца, в 50 скважинах - меди, в 100 скважинах - олова, а в остальных - содержание указанных металлов было на среднем уровне. Наугад выбирают скважину для повторного измерения. Найти вероятность того, что в ней окажется повышенное содержание меди, золота или марганца. Ответ введите с точностью до 3-го знака после запятой
0,061
В двух ящиках были доставлены образцы гранитов и песчаников. При этом в первом ящике находится 10 образцов, из них 3 гранитных, а во втором ящике - 15 образцов, из которых 6 гранитных. Из каждого ящика наудачу извлекают по образцу. Найти вероятность того, что оба образца окажутся гранитными. Ответ введите с точностью до 2-го знака после запятой
0,12
В партии образцов, привезенных с полевых работ, 5 % были золотосодержащими. Какова вероятность того, что из взятых наугад 5 образцов будет 2 золотосодержащих? Ответ введите с точностью до 3-го знака после запятой
0,024
При изучении упругих свойств образцов материалов получили следующие значения скоростей распространения упругих волн: 5,66; 5,86; 5,66; 5,76; 5,82; 5,54; 6,12; 5,54; 6,12; 5,82; 6,28; 5,94. Среднее значение ![math]() в этому виду материалов равно 5,80. Построить новый ряд отклонения экспериментальных данных от среднего по породе. Вычислить среднее, дисперсию и среднеквадратическое отклонение для этого ряда
в этому виду материалов равно 5,80. Построить новый ряд отклонения экспериментальных данных от среднего по породе. Вычислить среднее, дисперсию и среднеквадратическое отклонение для этого ряда
 в этому виду материалов равно 5,80. Построить новый ряд отклонения экспериментальных данных от среднего по породе. Вычислить среднее, дисперсию и среднеквадратическое отклонение для этого ряда
в этому виду материалов равно 5,80. Построить новый ряд отклонения экспериментальных данных от среднего по породе. Вычислить среднее, дисперсию и среднеквадратическое отклонение для этого ряда
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Каждая из первых пяти последовательных букв русского алфавита написана на отдельной карточке. Все карточки перемешиваются на столе "вниз лицом". Какова вероятность того, что из выбранных наугад четырех карточек получится слово: "беда". Ответ введите с точностью до целых.
0
Охотник выстрелил 3 раза по улетающей от него утке. Причем если вероятность попадания в утку при первом выстреле у охотника была 0,7, то после каждого выстрела она уменьшалась на 0,1. Вычислить вероятность попасть в утку только один раз. Ответ введите с точностью до 2-го знака после запятой
0,29
Вероятность положительной пробы в каждом из 100 независимых анализов равна 0,8. Найти вероятность того, что положительный результат будет зарегистрирован 90 раз. Ответ введите с точностью до 4-го знака после запятой
0,1234
Приемщица за 1 час принимает 2 заявки от клиентов. Предполагается простейший поток заявок (распределение Пуассона). Чему равна вероятность поступления не менее четырех заявок за 4 часа? Ответ введите с точностью до 4-го знака после запятой
0,9576
На столе лежало 36 экзаменационных билетов, перемешанных предварительно преподавателем. Студент знает только первые четыре билета (номера с 1 по 4). Он подходит к столу и берет билет. Какова вероятность того, что ему попадется билет один из тех, которые он знает? Ответ введите с точностью до 2-го знака после запятой
0,11
В геологическое управление поступили отчеты из трех районов. Из первого района 0,3 % отчетов содержали сведения о новых крупных месторождениях, из второго 0,2 %, а из третьего 0,4 %. Найти вероятность того, что данный отчет содержит сведения о крупном месторождении, если из первого района поступило 1000 отчетов, из второго 2000, из третьего 2500. Ответ введите с точностью до 3-го знака после запятой
0,003
Принимая равновероятным рождение мальчика и девочки, найти вероятность того, что из 4500 новорожденных будет 2300 мальчиков. Ответ введите с точностью до 2-го знака после запятой
0,13
Задача 12. Случайная непрерывная величина ![math]() задана функцией распределения . Требуется найти математическое ожидание и дисперсию
задана функцией распределения . Требуется найти математическое ожидание и дисперсию ![math]()
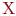 задана функцией распределения . Требуется найти математическое ожидание и дисперсию
задана функцией распределения . Требуется найти математическое ожидание и дисперсию 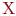
(1) M = 4; D = 1/3
(2) M = 2; D = 1/3
(3) M = 2; D = 4/3
(4) M = 4; D = 4/3
Друзья Александр, Виктор и Павел были заядлыми охотниками, но стреляли неважно. Один попадал в летящую утку с вероятностью 1/3, второй 2/5 и третий 1/4. У Василия был день рождения, и Александр, Виктор и Павел решили сделать ему подарок. Они одновременно выстрелили по пролетающей утке. Какова вероятность того, что за праздничным ужином будет подана убитая друзьями утка, если для этого достаточно хотя бы одного попадания? Если друзья стреляли друг за другом, изменится ли вероятность?
(1) 0,6 да
(2) 0,6 нет
(3) 0,7 да
(4) 0,8 нет
Некоторый медицинский прибор может быть изготовлен на трех различных заводах с вероятностями 0,25; 0,5; 0,25. Вероятности того, что прибор проработает два гарантийных срока, равны соответственно 0,1; 0,2 и 0,4. Найти вероятность того, что прибор проработает два гарантийных срока. Ответ введите с точностью до 3-го знака после запятой
0,225
Вероятность того, что рабочему отряда, отправляющегося в поле, понадобится обувь 41-го размера, равна 0,2. Какова вероятность того, что из 10 000 заказов на обувь со склада доля заказов обуви 41-го размера отклонится от вероятности 0,2 не более чем на 0,005? Ответ введите с точностью до 2-го знака после запятой
0,36
На тренировке спортсмен кидает копья, которые летят вдоль оси ![math]() . Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит от 35 до 40м. Ответ введите с точностью до 3-го знака после запятой
. Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит от 35 до 40м. Ответ введите с точностью до 3-го знака после запятой
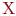 . Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит от 35 до 40м. Ответ введите с точностью до 3-го знака после запятой
. Предполагая, что копья совершенно одинаковые и дальность полета копья распределена нормально с математическим ожиданием 32 м и среднеквадратическим отклонением 5 м, найти, вероятность того, что копье пролетит от 35 до 40м. Ответ введите с точностью до 3-го знака после запятой
0,195
Лаборант из 1000 образцов производит выборку в 50 образцов. Найти вероятность того, что в выборке не окажется образцов, помеченных краской, если таких образцов 4.(предположить, что образцы извлекаются автоматически одновременно). Ответ введите с точностью до 3-го знака после запятой
0,814
Какова вероятность того, что два носка, взятые наудачу из ящика, в котором лежат 6 носков одного цвета, 3 носка - другого, будут из одной пары? Ответ введите с точностью до 1-го знака после запятой
0,5
Случайная величина ![math]() задана следующей функцией распределения: . Найти вероятность того, что в результате испытания
задана следующей функцией распределения: . Найти вероятность того, что в результате испытания ![math]() примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу ![math]() . Ответ введите с точностью до 1-го знака после запятой
. Ответ введите с точностью до 1-го знака после запятой
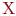 задана следующей функцией распределения: . Найти вероятность того, что в результате испытания
задана следующей функцией распределения: . Найти вероятность того, что в результате испытания 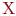 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  . Ответ введите с точностью до 1-го знака после запятой
. Ответ введите с точностью до 1-го знака после запятой
0,5
В выработке для передвижения по горизонтам использовали небольшие поезда, состоящие из 3 вагончиков по 6 мест в каждом. 9 шахтеров рассаживаются в таком поезде. Какова вероятность того, что в один из вагонов сядут четверо, во второй трое, в третий - двое? Ответ введите с точностью до 2-го знака после запятой
0,16
Время, необходимое для устранения неисправности в сейсмографе, есть случайная величина ![math]() , имеющая интегральную функцию распределения: , где
, имеющая интегральную функцию распределения: , где ![math]() - время, затраченное на конкретный ремонт;
- время, затраченное на конкретный ремонт; ![math]() - параметр, определяющий характер и сложность неисправности (считать постоянной). Найти математическое ожидание (среднее) времени обслуживания сейсмографа
- параметр, определяющий характер и сложность неисправности (считать постоянной). Найти математическое ожидание (среднее) времени обслуживания сейсмографа
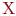 , имеющая интегральную функцию распределения: , где
, имеющая интегральную функцию распределения: , где  - время, затраченное на конкретный ремонт;
- время, затраченное на конкретный ремонт;  - параметр, определяющий характер и сложность неисправности (считать постоянной). Найти математическое ожидание (среднее) времени обслуживания сейсмографа
- параметр, определяющий характер и сложность неисправности (считать постоянной). Найти математическое ожидание (среднее) времени обслуживания сейсмографа
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В круг вписан квадрат. Какова вероятность того, что точка, брошенная наудачу в круг, окажется внутри квадрата?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

В некоторый полевой сезон исследовались два района. В первый было направлено 6 партий по 10 человек в каждой и 4 партии по 40 человек, а во второй район - 8 партий по 50 человек и 2 партии по 20 человек. Найти средний размер партии, которые работали в этом сезоне
(1) по 22 человека в одной партии
(2) по 33 человека в одной партии
(3) по 44 человека в одной партии
(4) по 30 человек в одной партии
На небольшом телефонном узле подсчитали, что каждые 4 мин звонит женщина, а каждые 6 мин - мужчина. Если принять за нулевой момент времени про¬извольный, то тогда можно считать, что звонок от женщины равновероятен от 0 до 4 мин, а от мужчин - от 0 до 6 мин. Определить вероятность того, что: в течение 2 мин будет любой звонок. Ответ введите с точностью до 2-го знака после запятой
0,67
Построить вариационный ряд, начертить полигон частот
| 76 | 87 | 1 | 6 | 68 | 85 | 67 | 40 | 72 | 80 | 65 | 56 |
| 57 | 58 | 61 | 3 | 43 | 15 | 36 | 9 | 72 | 91 | 73 | 60 |
| 60 | 68 | 37 | 24 | 59 | 9 | 41 | 90 | 42 | 19 | 41 | 33 |
| 45 | 74 | 1 | 28 | 2 | 11 | 30 | 35 | 72 | 40 | 8 | |
| 18 | 1 | 69 |
| Интервалы | Количество |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 19 | 10 |
| 37 | 7 |
| 55 | 7 |
| 73 | 17 |
| 91 | 7 |
| 109 | 0 |
| Интервалы | Количество |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 14 | 7 |
| 27 | 4 |
| 40 | 6 |
| 52 | 7 |
| 65 | 8 |
| 78 | 11 |
| Интервалы | Количество |
|---|---|
| 1 | 2 |
| 16 | 8 |
| 31 | 5 |
| 46 | 11 |
| 61 | 7 |
| 76 | 12 |
| 91 | 5 |
| Интервалы | Количество |
|---|---|
| 1 | 2 |
| 14 | 7 |
| 27 | 4 |
| 40 | 6 |
| 52 | 7 |
| 65 | 8 |
| 78 | 11 |
| 91 | 5 |



(1) таблица 3, Диаграмма 2
(2) таблица 2, Диаграмма 3
(3) таблица 1, Диаграмма 1
(4) таблица 4, Диаграмма 1
Два студента договорились встретиться в библиотеке с 13 до 14. Чтобы не обговаривать момент встречи решили так. Первый, кто приходит, ждет 15 минут и уходит. Какова вероятность, что студенты встретятся? Ответ введите с точностью до 2-го знака после запятой
0,44