Главная /
Математика /
Дифференциальные уравнения
Дифференциальные уравнения - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс содержит основные сведения, которые используются далее в теории уравнений математической физики и непосредственно при решении конкретных задач математики, физики и различных прикладных областей.
Все ответы: Курс содержит основные сведения, которые используются далее в теории уравнений математической физики и непосредственно при решении конкретных задач математики, физики и различных прикладных областей.
Составьте дифференциальное уравнение семейства кривых: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите преобразование Лапласа ![math]() от постоянной функции
от постоянной функции ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]() .
.
 от постоянной функции
от постоянной функции  . В ответе укажите его значение при
. В ответе укажите его значение при  .
.
(1) 5
(2) 8
(3) 12
(4) 15
Решите простейшую вариационную задачу для функционала
В ответе введите значение ![math]() .
.
 .
.
(1) 2
(2) 3
(3) 4
(4) 9
При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 2
(2) 3
(3) 4
(4) 5
Определить тип особой точки линейной невырожденной системы
(1) невырожденный узел
(2) вырожденный узел
(3) седло
(4) центр
(5) фокус
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 2
(2) 3
(3) 4
(4) 5
Найти матрицу ![math]() линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при
линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при ![math]() .
.
 линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при
линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при  .
.
(1) 2
(2) 3
(3) 5
(4) 10
Вычислите определитель Вронского системы, состоящей из функций ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
 и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) 1
(2) 2
(3) 3
(4) 4
Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) 10
(2) 20
(3) 30
(4) 40
Найдите изображение ![math]() оригинала
оригинала ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]() .
.
 оригинала
оригинала  . В ответе укажите его значение при
. В ответе укажите его значение при  .
.
(1) 60
(2) 70
(3) 80
(4) 90
Решите простейшую вариационную задачу для функционала
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции 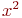 и
и  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
является седлом.
, при которых особая точка системы
является седлом.
 , при которых особая точка системы
является седлом.
, при которых особая точка системы
является седлом.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

У системы
с помощью первого интеграла определите тип (характер) нулевого положения равновесия.
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Вычислите значение при ![math]() определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
 определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) -1, да
(2) -1, нет
(3) 1, да
(4) 1, нет
Вычислите определитель Вронского системы, состоящей из функций ![math]() ,
, ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
 ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 3
(2) 5
(3) 7
(4) 9
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) -1
(2) 1
(3) -10
(4) 10
Вычислите значение при ![math]() преобразование Лапласа от оригинала
преобразование Лапласа от оригинала ![math]() .
.
 преобразование Лапласа от оригинала
преобразование Лапласа от оригинала  .
.
(1) 10
(2) 20
(3) 30
(4) 40
Найдите все значения вещественного параметра $a$, при которых на допустимой экстремали достигается минимум
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите производную по параметру ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения
удовлетворяющее начальному условию ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]() .
.
 . В ответе укажите его значение
. В ответе укажите его значение  .
.
(1) 12
(2) 18
(3) 24
(4) 30
Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
 , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() ,
, ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() при
при ![math]() .
.
 ,
,  и
и  . В ответе укажите значение
. В ответе укажите значение  при
при  .
.
(1) 5
(2) 10
(3) 15
(4) 20
Вычислите значение при ![math]() определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
 определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) 1, да
(2) 1, нет
(3) 0, да
(4) 0, нет
Составьте линейное однородное дифференциальное уравнение вида
наименьшего порядка ![math]() , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите ![math]() .
.
 , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 2
(2) 5
(3) 8
(4) 10
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его предел при
. В ответе укажите его предел при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его предел при
. В ответе укажите его предел при 
(1) -2
(2) 2
(3) -4
(4) 4
Восстановите оригинал ![math]() по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение ![math]() .
.
 по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение  .
.
(1) 16
(2) 24
(3) 32
(4) 40
Решите вариационную задачу со свободным концом
В ответе укажите значение ![math]()

(1) 2
(2) 3
(3) 6
(4) 11
Найдите производную по начальному условию ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . В какой точке оно пересекает окружность с центром в начале координат и радиусом
. В какой точке оно пересекает окружность с центром в начале координат и радиусом ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . В какой точке оно пересекает окружность с центром в начале координат и радиусом
. В какой точке оно пересекает окружность с центром в начале координат и радиусом  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
 , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() ,
, ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 1
(2) 2
(3) 3
(4) 8
Найти значение при ![math]() определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при ![math]() равно
равно ![math]() .
.
 определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при  равно
равно  .
.
(1) 2
(2) 3
(3) 6
(4) 9
Известны два частных решения линейного неоднородного уравнения первого порядка: ![math]() и
и ![math]() . Найдите решение с начальным условием
. Найдите решение с начальным условием ![math]() .
.
 и
и  . Найдите решение с начальным условием
. Найдите решение с начальным условием  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 2
(2) 4
(3) 6
(4) 8
Решите уравнение Эйлера ![math]() при
при ![math]() . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение её решения при
. В ответе укажите значение её решения при ![math]()
 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 
(1) 1
(2) 2
(3) 3
(4) 4
Решите операционным методом задачу Коши ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите вариационную задачу без ограничений
В ответе укажите значение ![math]() .
.
 .
.
(1) -12
(2) -6
(3) 6
(4) 12
Методом введения параметра найдите решение уравнения ![math]() с начальными условиями
с начальными условиями ![math]() ,
, ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 с начальными условиями
с начальными условиями  ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -4
(2) -3
(3) 3
(4) 4
Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение её решения при
. В ответе укажите значение её решения при ![math]()
 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 
(1) 0
(2) 2
(3) 5
(4) 7
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите общее решение системы дифференциальных уравнений
В ответе укажите абсциссу точки пересечения плоскости ![math]() и решения, проходящего через точку
и решения, проходящего через точку ![math]() .
.
 и решения, проходящего через точку
и решения, проходящего через точку  .
.
(1) 1
(2) 3
(3) 5
(4) 7
Найти значение при ![math]() определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при ![math]() равно
равно ![math]() .
.
 определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при  равно
равно  .
.
(1) 0
(2) 1
(3) 2
(4) 3
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]() при
при ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение  при
при 
(1) 2
(2) 4
(3) 6
(4) 8
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами
наименьшего порядка ![math]() , которое имеет частное решение
, которое имеет частное решение ![math]() . В ответе укажите сумму
. В ответе укажите сумму ![math]()
 , которое имеет частное решение
, которое имеет частное решение  . В ответе укажите сумму
. В ответе укажите сумму 
(1) -1
(2) 0
(3) 1
(4) 2
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) 0
(2) 2
(3) 5
(4) 6
Найдите траекторию, проходящую через точку ![math]() и ортогональную семейству кривых
и ортогональную семейству кривых ![math]() . Укажите значение
. Укажите значение ![math]() , при котором она пересекает прямую
, при котором она пересекает прямую ![math]()
 и ортогональную семейству кривых
и ортогональную семейству кривых  . Укажите значение
. Укажите значение  , при котором она пересекает прямую
, при котором она пересекает прямую 
(1) 0
(2) 2
(3) 4
(4) 6
Решите операционным методом задачу Коши ![math]() ,
, ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -1
(2) 0
(3) 1
(4) 2
Исследовать функционал на экстремум:
В ответе введите значение ![math]() .
.
 .
.
(1) 12
(2) 15
(3) 45
(4) 60
Найдите особое решение уравнения ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 5
(2) 6
(3) 9
(4) 10
Найдите значение ![math]() функции, удовлетворяющей дифференциальному уравнению
функции, удовлетворяющей дифференциальному уравнению ![math]() и начальному условию
и начальному условию ![math]()
 функции, удовлетворяющей дифференциальному уравнению
функции, удовлетворяющей дифференциальному уравнению  и начальному условию
и начальному условию 
(1) -3
(2) -1
(3) 1
(4) 3
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  .
.
(1) 10
(2) 15
(3) 18
(4) 20
Система
имеет решение
Найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -12
(2) -9
(3) -6
(4) -3
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 1
(2) 2
(3) 3
(4) 4
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 2
(2) 4
(3) 6
(4) 8
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) -3
(2) -1
(3) 1
(4) 3
В баке находится 100 л раствора, содержащего 1 кг соли. В бак непрерывно подаётся вода (5 л в минуту), которая перемешивается с имеющимся раствором. Смесь вытекает с той же скоростью. Сколько граммов соли останется в баке через час? (Ответ округлить до целого числа.)
(1) 20
(2) 50
(3) 100
(4) 150
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -7
(2) -5
(3) -2
(4) 5
Решите изопериметрическую вариационную задачу
В ответе укажите значение ![math]() .
.
 .
.
(1) -4
(2) 0
(3) 2
(4) 4
Методом введения параметра найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -6
(2) -3
(3) 0
(4) 3
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению.
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению.
и начальному условию
В ответе укажите значение ![math]() .
.
 , удовлетворяющую дифференциальному уравнению.
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению.
и начальному условию
В ответе укажите значение  .
.
(1) 123
(2) 132
(3) 213
(4) 231
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -4
(2) 4
(3) 6
(4) 8
Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) 2
(2) 4
(3) 6
(4) 8
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 1
(2) 2
(3) 3
(4) 4
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  ,
,  .
.
(1) 3
(2) 5
(3) 7
(4) 9
За 30 дней распадается 50% радиоактивного вещества. За сколько дней распадётся 99% его первоначального количества? (Скорость распада радиоактивного вещества пропорциональна его оставшемуся количеству.)
(1) 60
(2) 120
(3) 200
(4) 240
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите изопериметрическую вариационную задачу
В ответе укажите значение ![math]() .
.
 .
.
(1) -2
(2) -1
(3) 1
(4) 2
Найдите особое решение уравнения
При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 оно пересекает прямую
оно пересекает прямую  ?
?
(1) 3
(2) 6
(3) 8
(4) 9
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() при
при ![math]() ,
, ![math]() и
и ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  при
при  ,
,  и
и  .
.
(1) 68
(2) 69
(3) 96
(4) 86
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -8
(2) -2
(3) 3
(4) 15
Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 2
(2) 3
(3) 4
(4) 5
Найдите наименьшее вещественное значение ![math]() , при котором краевая задача
имеет ненулевое решение.
, при котором краевая задача
имеет ненулевое решение.
 , при котором краевая задача
имеет ненулевое решение.
, при котором краевая задача
имеет ненулевое решение.
(1) 0
(2) 2
(3) 4
(4) 6
Найдите ![math]() , если
, если ![math]() и
и
 , если
, если  и
и
(1) 16
(2) 24
(3) 32
(4) 40
Какое наименьшее число нулей может иметь нетривиальное решение уравнения ![math]() на интервале длины
на интервале длины ![math]() ?
?
 на интервале длины
на интервале длины  ?
?
(1) 7
(2) 14
(3) 20
(4) 25
Какое наибольшее число нулей может иметь нетривиальное решение уравнения ![math]() на отрезке длины
на отрезке длины ![math]() ?
?
 на отрезке длины
на отрезке длины  ?
?
(1) 0
(2) 1
(3) 2
(4) 3
Какое наибольшее число нулей может иметь нетривиальное решение уравнения ![math]() на отрезке длины 100?
на отрезке длины 100?
 на отрезке длины 100?
на отрезке длины 100?
(1) 0
(2) 1
(3) 2
(4) 3
Вещественная функция ![math]() определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения ![math]() ?
?
 определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наибольшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения  ?
?
(1) 0
(2) 1
(3) 2
(4) 3
Составьте дифференциальное уравнение семейства кривых: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите преобразование Лапласа ![math]() от функции
от функции ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]() .
.
 от функции
от функции  . В ответе укажите его значение
. В ответе укажите его значение  .
.
(1) 14
(2) 24
(3) 34
(4) 44
Решите простейшую вариационную задачу для функционала
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -9
(2) -6
(3) -3
(4) 5
Определить тип особой точки линейной невырожденной системы
(1) невырожденный узел
(2) вырожденный узел
(3) седло
(4) центр
(5) фокус
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 1
(2) 6
(3) 12
(4) 25
Найти матрицу ![math]() линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при
линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при ![math]()
 линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при
линейной однородной системы
зная её фундаментальную матрицу
В ответе укажите значение суммы всех элементов найденной матрицы при 
(1) -10
(2) -6
(3) 6
(4) 10
Вычислите определитель Вронского системы, состоящей из функций ![math]() ,
, ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
 ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]()

(1) -2
(2) -1
(3) 0
(4) 1
Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -5
(2) 0
(3) 5
(4) 12
Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) 1
(2) 2
(3) 3
(4) 4
Вычислите значение при ![math]() преобразование Лапласа от оригинала
преобразование Лапласа от оригинала ![math]() .
.
 преобразование Лапласа от оригинала
преобразование Лапласа от оригинала  .
.
(1) 18
(2) 24
(3) 36
(4) 42
Решите простейшую вариационную задачу для функционала
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите значение вещественного параметра ![math]() , при котором особая точка системы
является центром.
, при котором особая точка системы
является центром.
 , при котором особая точка системы
является центром.
, при котором особая точка системы
является центром.
(1) 0
(2) 1
(3) 2
(4) 3
У системы
с помощью первого интеграла определите тип (характер) нулевого положения равновесия.
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Вычислите значение при ![math]() определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
 определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) 2, да
(2) 2, нет
(3) 4, да
(4) 4, нет
Вычислите определитель Вронского системы, состоящей из функций ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
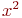 и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 3
(2) 5
(3) 7
(4) 9
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) -1
(2) 1
(3) -10
(4) 10
Вычислите значение при ![math]() преобразование Лапласа от оригинала
преобразование Лапласа от оригинала ![math]() .
.
 преобразование Лапласа от оригинала
преобразование Лапласа от оригинала  .
.
(1) 7
(2) 14
(3) 21
(4) 28
Найдите все значения вещественного параметра ![math]() , при которых на допустимой экстремали достигается минимум
, при которых на допустимой экстремали достигается минимум
 , при которых на допустимой экстремали достигается минимум
, при которых на допустимой экстремали достигается минимум
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите производную по параметру ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения
проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 7
(2) 13
(3) 19
(4) 21
Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
 , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() ,
, ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 0
(2) 1
(3) 3
(4) 5
Вычислите значение при ![math]() определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
 определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) 1, да
(2) 1, нет
(3) 0, да
(4) 0, нет
Составьте линейное однородное дифференциальное уравнение вида
наименьшего порядка ![math]() , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите ![math]() .
.
 , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение
(1) 0
(2) 1
(3) 2
(4) 3
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите абсциссу точки пересечения прямой ![math]() и решения уравнения
и решения уравнения ![math]() , проходящего через точку
, проходящего через точку ![math]()
 и решения уравнения
и решения уравнения  , проходящего через точку
, проходящего через точку 
(1) -1
(2) 0
(3) 1
(4) 2
Восстановите оригинал ![math]() по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение ![math]() .
.
 по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение  .
.
(1) 30
(2) 45
(3) 60
(4) 75
Решите вариационную задачу со свободным концом
В ответе укажите значение ![math]() .
.
 .
.
(1) 2
(2) 12
(3) 14
(4) 97
Найдите производную по начальному условию ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
 , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите общее решение системы дифференциальных уравнений
В ответе укажите значение координаты ![math]() точки пересечения плоскости
точки пересечения плоскости ![math]() и решения, проходящего через точку
и решения, проходящего через точку ![math]() .
.
 точки пересечения плоскости
точки пересечения плоскости  и решения, проходящего через точку
и решения, проходящего через точку  .
.
(1) 0
(2) 1
(3) 3
(4) 4
Два решения ![math]() и
и ![math]() системы
удовлетворяют начальным условиям:
Найдите их определитель Вронского
системы
удовлетворяют начальным условиям:
Найдите их определитель Вронского ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 и
и  системы
удовлетворяют начальным условиям:
Найдите их определитель Вронского
системы
удовлетворяют начальным условиям:
Найдите их определитель Вронского  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 0
(2) 2
(3) 4
(4) 6
Известны три частных решения линейного неоднородного уравнения второго порядка: ![math]() ,
, ![math]() и
и ![math]() . Найдите решение с начальным условием
. Найдите решение с начальным условием ![math]() ,
, ![math]() .
.
 ,
,  и
и  . Найдите решение с начальным условием
. Найдите решение с начальным условием  ,
,  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 2
(2) 3
(3) 4
(4) 7
Решите уравнение Эйлера ![math]() при
при ![math]() . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) 1
(5) 0
(6) ![math]()

Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение её решения при
. В ответе укажите значение её решения при ![math]()
 ,
,  . В ответе укажите значение её решения при
. В ответе укажите значение её решения при 
(1) -25
(2) 25
(3) -2
(4) 2
Решите операционным методом задачу Коши ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -2
(2) 0
(3) 2
(4) 5
Найдите допустимые экстремали в задаче без ограничений
В ответе укажите значение ![math]() .
.
 .
.
(1) -2
(2) 0
(3) 4
(4) 6
Найдите особое решение уравнения ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -4
(2) -3
(3) -2
(4) -1
Решите задачу Коши
В ответе укажите значение её решения при ![math]()

(1) 2
(2) 10
(3) 20
(4) 22
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите общее решение системы дифференциальных уравнений
В ответе укажите абсциссу точки пересечения плоскости ![math]() и решения, проходящего через точку
и решения, проходящего через точку ![math]() .
.
 и решения, проходящего через точку
и решения, проходящего через точку  .
.
(1) 1
(2) 3
(3) 5
(4) 7
Найти значение при ![math]() определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при ![math]() равно
равно ![math]() .
.
 определителя фундаментальной матрицы системы
если его значение при
определителя фундаментальной матрицы системы
если его значение при  равно
равно  .
.
(1) 1
(2) 2
(3) 3
(4) 5
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() при
при ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите значение
. В ответе укажите значение  при
при 
(1) 18
(2) 36
(3) 54
(4) 72
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами
наименьшего порядка ![math]() , которое имеет частное решение
, которое имеет частное решение ![math]() . В ответе укажите сумму
. В ответе укажите сумму ![math]()
 , которое имеет частное решение
, которое имеет частное решение  . В ответе укажите сумму
. В ответе укажите сумму 
(1) -2
(2) -1
(3) 1
(4) 2
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) 1
(2) 2
(3) 3
(4) 4
Найдите траекторию, проходящую через точку ![math]() и ортогональную семейству кривых
и ортогональную семейству кривых ![math]() . Укажите значение
. Укажите значение ![math]() , при котором она пересекает прямую
, при котором она пересекает прямую ![math]()
 и ортогональную семейству кривых
и ортогональную семейству кривых  . Укажите значение
. Укажите значение  , при котором она пересекает прямую
, при котором она пересекает прямую 
(1) -6
(2) 6
(3) -90
(4) 90
Решите операционным методом задачу Коши ![math]() ,
, ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Исследовать функционал на экстремум:
В ответе введите значение производной ![math]() .
.
 .
.
(1) 0
(2) 2
(3) 5
(4) 12
Методом введения параметра найдите решение уравнения ![math]() с начальными условиями
с начальными условиями ![math]() ,
, ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 с начальными условиями
с начальными условиями  ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 4
(2) 6
(3) 8
(4) 10
Найдите значение ![math]() функции, удовлетворяющей дифференциальному уравнению
функции, удовлетворяющей дифференциальному уравнению ![math]() и начальному условию
и начальному условию ![math]()
 функции, удовлетворяющей дифференциальному уравнению
функции, удовлетворяющей дифференциальному уравнению  и начальному условию
и начальному условию 
(1) 2
(2) 3
(3) 4
(4) 5
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  .
.
(1) 2
(2) 5
(3) 7
(4) 9
Система
имеет решение
Найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 0
(2) 1
(3) 2
(4) 4
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 1
(2) 2
(3) 4
(4) 5
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 0
(2) 2
(3) 4
(4) 6
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) -2
(2) -1
(3) 1
(4) 2
В воздухе комнаты объёмом 200 куб. м содержится 0,15% углекислого газа. Вентилятор подаёт в минуту 20 куб. м воздуха содержащего 0,04% углекислого газа. Через сколько минут количество углекислого газа в воздухе комнаты уменьшится втрое? (Ответ округлить до целого числа.)
(1) 15
(2) 20
(3) 24
(4) 32
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 2
(2) 3
(3) 5
(4) 7
Решите изопериметрическую вариационную задачу
В ответе укажите значение ![math]() .
.
 .
.
(1) 2
(2) 3
(3) 6
(4) 8
Найдите особое решение уравнения ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -6
(2) -3
(3) 0
(4) 3
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  .
.
(1) -1
(2) 0
(3) 1
(4) 2
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 0
(2) 1
(3) 2
(4) 3
Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) -10
(2) -1
(3) 1
(4) 10
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 6
(2) 9
(3) 36
(4) 72
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  .
.
(1) 0
(2) 1
(3) 2
(4) 3
Цилиндрический бак поставлен вертикально и имеет отверстие в дне. Половина воды из полного бака вытекает за 5 минут. За сколько минут из полного бака вытечет вся вода? (Квадрат скорости вытекания воды из бака пропорционален высоте уровня оставшейся воды над отверстием.)
(1) 10
(2) 12
(3) 15
(4) 17
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение
![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение
 .
.
(1) 3
(2) 4
(3) 5
(4) 6
Найдите допустимые экстремали ![math]() изопериметрической задачи
В ответе введите значение
изопериметрической задачи
В ответе введите значение ![math]()
 изопериметрической задачи
В ответе введите значение
изопериметрической задачи
В ответе введите значение 
(1) -3
(2) 0
(3) 2
(4) 8
Методом введения параметра найдите решение уравнения
с начальными условиями ![math]() ,
, ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 5
(2) 6
(3) 7
(4) 8
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() при
при ![math]() ,
, ![math]() и
и ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  при
при  ,
,  и
и  .
.
(1) 42
(2) 43
(3) 44
(4) 45
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 32
(2) 64
(3) 128
(4) 256
Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 2
(2) 3
(3) 4
(4) 9
Найдите наименьшее вещественное значение ![math]() , при котором краевая задача
не имеет решений.
, при котором краевая задача
не имеет решений.
 , при котором краевая задача
не имеет решений.
, при котором краевая задача
не имеет решений.
(1) 0
(2) 2
(3) 4
(4) 6
Найдите ![math]() , если
, если ![math]() и
и
 , если
, если  и
и
(1) 0
(2) 5
(3) 10
(4) 15
Какое наибольшее число нулей может иметь нетривиальное решение уравнения ![math]() на отрезке длины
на отрезке длины ![math]() ?
?
 на отрезке длины
на отрезке длины  ?
?
(1) 20
(2) 25
(3) 40
(4) 50
Какое наименьшее число нулей может иметь нетривиальное решение уравнения ![math]() на отрезке длины 100?
на отрезке длины 100?
 на отрезке длины 100?
на отрезке длины 100?
(1) 0
(2) 1
(3) 2
(4) 3
Какое наибольшее число нулей может иметь нетривиальное решение уравнения
на отрезке длины 100?
(1) 24
(2) 48
(3) 96
(4) 192
Вещественная функция ![math]() определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения ![math]() ?
?
 определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения  ?
?
(1) 0
(2) 1
(3) 2
(4) 3
Составьте дифференциальное уравнение семейства кривых: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите изображение ![math]() оригинала
оригинала ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]() .
.
 оригинала
оригинала  . В ответе укажите его значение при
. В ответе укажите его значение при  .
.
(1) 14
(2) 24
(3) 34
(4) 44
Решите простейшую вариационную задачу для функционала
В ответе введите значение ![math]() .
.
 .
.
(1) 2
(2) 3
(3) 5
(4) 6
При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
(1) 2
(2) 3
(3) 4
(4) 5
Найдите решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определить тип особой точки линейной невырожденной системы
(1) невырожденный узел
(2) вырожденный узел
(3) седло
(4) центр
(5) фокус
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 и
и  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 3
(2) 6
(3) 18
(4) 24
Найдите фундаментальную матрицу ![math]() системы
если
системы
если ![math]() (
(![math]() - единичная матрица). В ответе укажите сумму собственных чисел матрицы
- единичная матрица). В ответе укажите сумму собственных чисел матрицы ![math]() .
.
 системы
если
системы
если  (
( - единичная матрица). В ответе укажите сумму собственных чисел матрицы
- единичная матрица). В ответе укажите сумму собственных чисел матрицы  .
.
(1) 0
(2) 5
(3) 10
(4) 15
Вычислите определитель Вронского системы, состоящей из функций ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
 и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]()

(1) -1
(2) 0
(3) 1
(4) 2
Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -9
(2) 0
(3) 4
(4) 9
Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) 10
(2) 51
(3) 81
(4) 101
Вычислите значение при ![math]() преобразование Лапласа от оригинала
преобразование Лапласа от оригинала ![math]() .
.
 преобразование Лапласа от оригинала
преобразование Лапласа от оригинала  .
.
(1) 6
(2) 12
(3) 18
(4) 24
Решите простейшую вариационную задачу для функционала
В ответе введите значение ![math]() .
.
 .
.
(1) -8
(2) -3
(3) 2
(4) 8
При каком наименьшем ![math]() уравнение вида
уравнение вида ![math]() , где
, где ![math]() - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции ![math]() и
и ![math]() ?
?
 уравнение вида
уравнение вида  , где
, где  - непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции
- непрерывно дифференцируемая функция на плоскости, может иметь среди своих решений функции  и
и  ?
?
(1) 3
(2) 4
(3) 5
(4) 6
Найдите решение уравнения ![math]() , проходящее через точку
, проходящее через точку ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 , проходящее через точку
, проходящее через точку  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

У системы
с помощью первого интеграла определите тип (характер) нулевого положения равновесия.
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Вычислите значение при $t=10$ определителя Вронского двух вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) 1, да
(2) 1, нет
(3) 0, да
(4) 0, нет
Вычислите определитель Вронского системы, состоящей из функций ![math]() ,
, ![math]() и
и ![math]() . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
 ,
,  и
и  . Являются эти функции линейно зависимыми?
. Являются эти функции линейно зависимыми?
(1) -1 да
(2) -1 нет
(3) 1 да
(4) 1 нет
(5) 0 да
(6) 0 нет
Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 1
(2) 2
(3) 3
(4) 4
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![math]() . В ответе укажите его значение при
. В ответе укажите его значение при ![math]()
 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  . В ответе укажите его значение при
. В ответе укажите его значение при 
(1) 4
(2) 6
(3) 8
(4) 10
Восстановите оригинал ![math]() по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение ![math]() .
.
 по изображению
В ответе укажите его значение
по изображению
В ответе укажите его значение  .
.
(1) 15
(2) 30
(3) 45
(4) 60
Решите вариационную задачу со свободным концом
В ответе укажите значение ![math]() .
.
 .
.
(1) -8
(2) 0
(3) 2
(4) 8
Найдите производную по параметру ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения
удовлетворяющее начальному условию ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]() .
.
 . В ответе укажите его значение
. В ответе укажите его значение  .
.
(1) -2
(2) -1
(3) 1
(4) 2
Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
 , при которых особая точка системы
асимптотически устойчива.
, при которых особая точка системы
асимптотически устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите значение при ![math]() определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
 определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
определителя Вронского трёх вектор-функций
Являются ли эти вектор-функции линейно зависимыми?
(1) 1, да
(2) 1, нет
(3) 0, да
(4) 0, нет
Составьте линейное однородное дифференциальное уравнение вида
наименьшего порядка ![math]() , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите ![math]() .
.
 , которое имеет следующие частные решения:
В ответе укажите
, которое имеет следующие частные решения:
В ответе укажите  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение ![math]()

(1) -2
(2) 10
(3) -19
(4) 19
Решите задачу Коши ![math]() ,
, ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 ,
,  ,
,  . В ответе укажите значение
. В ответе укажите значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -1
(2) 0
(3) 1
(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите уравнения вертикальных асимптот решения задачи Коши
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Восстановите оригинал ![math]() по изображению
В ответе укажите значение его производной
по изображению
В ответе укажите значение его производной ![math]() .
.
 по изображению
В ответе укажите значение его производной
по изображению
В ответе укажите значение его производной  .
.
(1) -24
(2) -12
(3) 12
(4) 24
Решите вариационную задачу со свободным концом
В ответе укажите значение ![math]() .
.
 .
.
(1) 2
(2) 6
(3) 8
(4) 15
Найдите производную по начальному условию ![math]() при
при ![math]() от решения
от решения ![math]() задачи Коши:
при
задачи Коши:
при ![math]() .
.
 при
при  от решения
от решения  задачи Коши:
при
задачи Коши:
при  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите все значения вещественного параметра ![math]() , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
 , при которых особая точка системы
устойчива.
, при которых особая точка системы
устойчива.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Два решения ![math]() и
и ![math]() системы
удовлетворяют начальным условиям:
Найдите значение их определителя Вронского при
системы
удовлетворяют начальным условиям:
Найдите значение их определителя Вронского при ![math]() .
.
 и
и  системы
удовлетворяют начальным условиям:
Найдите значение их определителя Вронского при
системы
удовлетворяют начальным условиям:
Найдите значение их определителя Вронского при  .
.
(1) -64
(2) -54
(3) -44
(4) -34
Известны три частных решения линейного неоднородного уравнения второго порядка: ![math]() ,
, ![math]() и
и ![math]() . Найдите решение с начальным условием
. Найдите решение с начальным условием ![math]() ,
, ![math]() .
.
 ,
,  и
и  . Найдите решение с начальным условием
. Найдите решение с начальным условием  ,
,  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши:
В ответе укажите значение ![math]()

(1) 2
(2) 3
(3) 4
(4) 8
Решите уравнение Эйлера ![math]() при
при ![math]() . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 при
при  . Найдите решение, удовлетворяющее начальным условиям
. Найдите решение, удовлетворяющее начальным условиям  . В ответе укажите его значение
. В ответе укажите его значение 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение системы
удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите задачу Коши ![math]() ,
, ![math]() . В ответе укажите его предел при
. В ответе укажите его предел при ![math]()
 ,
,  . В ответе укажите его предел при
. В ответе укажите его предел при 
(1) 0
(2) 1
(3) 2
(4) 10
Решите операционным методом задачу Коши ![math]() ,
, ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 12
(2) 13
(3) 14
(4) 15
Исследовать функционал на экстремум:
В ответе введите значение ![math]() .
.
 .
.
(1) 0
(2) 1
(3) 8
(4) 12
Методом введения параметра найдите решение уравнения ![math]() с начальными условиями
с начальными условиями ![math]() ,
, ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 с начальными условиями
с начальными условиями  ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) -30
(2) -20
(3) -15
(4) -10
Решите задачу Коши
В ответе укажите значение её решения при ![math]()

(1) 2
(2) 10
(3) 14
(4) 18
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  .
.
(1) 3
(2) 4
(3) 12
(4) 24
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 6
(2) 9
(3) 17
(4) 36
Составьте линейное однородное дифференциальное уравнение с постоянными вещественными коэффициентами
наименьшего порядка ![math]() , которое имеет частные решения
, которое имеет частные решения ![math]() и
и ![math]() . В ответе укажите сумму
. В ответе укажите сумму ![math]()
 , которое имеет частные решения
, которое имеет частные решения  и
и  . В ответе укажите сумму
. В ответе укажите сумму 
(1) 2
(2) 4
(3) 6
(4) 8
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) 0
(2) 1
(3) 3
(4) 5
Найдите траекторию, проходящую через точку ![math]() и ортогональную семейству кривых
и ортогональную семейству кривых ![math]() . Укажите значения
. Укажите значения ![math]() , при котором она пересекает прямую
, при котором она пересекает прямую ![math]()
 и ортогональную семейству кривых
и ортогональную семейству кривых  . Укажите значения
. Укажите значения  , при котором она пересекает прямую
, при котором она пересекает прямую 
(1) -1
(2) 1
(3) -2
(4) 2
Решите операционным методом задачу Коши ![math]() ,
, ![math]() ,
, ![math]() при
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  ,
,  при
при  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -2
(2) -1
(3) 0
(4) 1
Найти допустимые экстремали ![math]() вариационной задачи:
В ответе введите значение
вариационной задачи:
В ответе введите значение ![math]() .
.
 вариационной задачи:
В ответе введите значение
вариационной задачи:
В ответе введите значение  .
.
(1) 2
(2) 10
(3) 30
(4) 60
Найдите особое решение уравнения ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Решите задачу Коши для дифференциального уравнения ![math]() с начальным условием
с начальным условием ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]()
 с начальным условием
с начальным условием  . В ответе укажите значение
. В ответе укажите значение 
(1) 2
(2) 4
(3) 6
(4) 8
У системы
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию ![math]() , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() при
при ![math]() и
и ![math]() .
.
 , удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение
, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение  при
при  и
и  .
.
(1) 15
(2) 17
(3) 19
(4) 21
Система
имеет решение
Найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() при
при ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  при
при  .
.
(1) 1
(2) 2
(3) 5
(4) 7
С помощью формулы Лиувилля-Остроградского решите задачу Коши:
В ответе укажите значение ![math]() .
.
 .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 2
(2) e-2
(3) e2
(4) e
(5) e-1
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 3
(2) 6
(3) 9
(4) 12
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() ,
, ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  ,
,  .
.
(1) -5
(2) 0
(3) 3
(4) 5
Чайник за 10 минут остыл от ![math]() до
до ![math]() . Температура воздуха в комнате
. Температура воздуха в комнате ![math]() . За сколько минут чайник остынет от
. За сколько минут чайник остынет от ![math]() до
до ![math]() ? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
 до
до  . Температура воздуха в комнате
. Температура воздуха в комнате  . За сколько минут чайник остынет от
. За сколько минут чайник остынет от  до
до  ? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
? (Скорость остывания тела пропорциональна разности температур тела и окружающей среды.)
(1) 20
(2) 25
(3) 30
(4) 35
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Решите изопериметрическую вариационную задачу
В ответе укажите значение ![math]() .
.
 .
.
(1) 2
(2) 4
(3) 9
(4) 12
Методом введения параметра найдите решение уравнения
с начальными условиями ![math]() ,
, ![math]() . При каком
. При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 ,
,  . При каком
. При каком  оно пересекает прямую
оно пересекает прямую  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Найдите функцию $u$, удовлетворяющую дифференциальному уравнению
и начальному условию
В ответе укажите значение ![math]() .
.
 .
.
(1) 2
(2) 5
(3) 10
(4) 12
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -4
(2) -2
(3) 4
(4) 5
Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 3
(2) 5
(3) 6
(4) 8
Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() ,
, ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  ,
,  . В ответе укажите его значение
. В ответе укажите его значение 
(1) 2
(2) 4
(3) 12
(4) 13
Найдите решение краевой задачи:
В ответе введите его значение при ![math]()

(1) 2
(2) 4
(3) 6
(4) 18
С помощью матричной экспоненты решите линейную однородную систему
В ответе укажите значение ![math]() при
при ![math]() для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям ![math]() .
.
 при
при  для решения, удовлетворяющего начальным условиям
для решения, удовлетворяющего начальным условиям  .
.
(1) 2
(2) 4
(3) 6
(4) 8
Парашютист прыгнул с высоты 1,5 км и раскрыл парашют на высоте 0,5 км. Сколько секунд он падал до раскрытия парашюта? (Ответ округлить до целого числа.) Известно, что предельная скорость падения человека в воздухе нормальной плотности равна 50 м/с. Изменением плотности с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.
(1) 19
(2) 21
(3) 23
(4) 25
Решите операционным методом задачу Коши
при ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -5
(2) -3
(3) 3
(4) 5
Найдите минимум функционала
если
(1) 2
(2) 4
(3) 6
(4) 8
Найдите особое решение уравнения
При каком ![math]() оно пересекает прямую
оно пересекает прямую ![math]() ?
?
 оно пересекает прямую
оно пересекает прямую  ?
?
(1) 1
(2) 2
(3) 3
(4) 4
Найдите общее решение уравнения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для уравнения
найдите положение равновесия и по первому приближению определите его тип (характер).
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр
Решите неоднородную систему
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) -12
(2) -4
(3) -3
(4) -2
Решите неоднородное уравнение
методом вариации постоянных и найдите решение, удовлетворяющее начальным условиям ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 . В ответе укажите значение
. В ответе укажите значение  .
.
(1) 2
(2) 4
(3) 8
(4) 16
Найдите решение уравнения ![math]() , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: ![math]() . В ответе укажите его значение
. В ответе укажите его значение ![math]()
 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:  . В ответе укажите его значение
. В ответе укажите его значение 
(1) -2
(2) -1
(3) 1
(4) 2
Найдите наименьшее вещественное значение ![math]() , при котором краевая задача
имеет бесконечно много решений.
, при котором краевая задача
имеет бесконечно много решений.
 , при котором краевая задача
имеет бесконечно много решений.
, при котором краевая задача
имеет бесконечно много решений.
(1) 4
(2) 8
(3) 12
(4) 16
Найдите ![math]() , если
, если ![math]() и
и
 , если
, если  и
и
(1) -1
(2) -2
(3) 1
(4) 3
Какое наименьшее число нулей может иметь нетривиальное решение уравнения ![math]() на интервале длины
на интервале длины ![math]() ?
?
 на интервале длины
на интервале длины  ?
?
(1) 0
(2) 5
(3) 10
(4) 15
Какое наименьшее число нулей может иметь нетривиальное решение уравнения ![math]() на отрезке длины 100?
на отрезке длины 100?
 на отрезке длины 100?
на отрезке длины 100?
(1) 4
(2) 7
(3) 9
(4) 63
Вещественная функция ![math]() определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения ![math]() ?
?
 определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения
определена, непрерывна и положительна на всей числовой прямой. Какое наименьшее число нулей может иметь на всей числовой прямой нетривиальное решение уравнения  ?
?
(1) 0
(2) 1
(3) 2
(4) 3
Напишите уравнение вида ![math]() , которому удовлетворяет функция
, которому удовлетворяет функция ![math]() и найдите его решение с начальными условиями
и найдите его решение с начальными условиями ![math]() ,
, ![math]() . В ответе укажите значение
. В ответе укажите значение ![math]() .
.
 , которому удовлетворяет функция
, которому удовлетворяет функция  и найдите его решение с начальными условиями
и найдите его решение с начальными условиями  ,
,  . В ответе укажите значение
. В ответе укажите значение  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определить тип особой точки линейной невырожденной системы
(1) невырожденный узел
(2) вырожденный узел
(3) седло
(4) центр
(5) фокус
Отыскав первый интеграл, найдите решение системы дифференциальных уравнений
удовлетворяющее начальным условиям ![math]() и
и ![math]() . В ответе укажите значение
. В ответе укажите значение
 и
и  . В ответе укажите значение
. В ответе укажите значение
(1) 0
(2) 6
(3) 10
(4) 15
Найдите фундаментальную матрицу ![math]() системы
если
системы
если ![math]() (
(![math]() - единичная матрица). В ответе укажите сумму всех элементов матрицы
- единичная матрица). В ответе укажите сумму всех элементов матрицы ![math]() .
.
 системы
если
системы
если  (
( - единичная матрица). В ответе укажите сумму всех элементов матрицы
- единичная матрица). В ответе укажите сумму всех элементов матрицы  .
.
(1) 5
(2) 10
(3) 15
(4) 20
У системы
с помощью первого интеграла определите тип (характер) нулевого положения равновесия.
(1) неустойчивый узел
(2) устойчивый узел
(3) седло
(4) неустойчивый фокус
(5) устойчивый фокус
(6) центр