Главная / Математика / Введение в теорию вероятностей

Введение в теорию вероятностей - ответы на тесты Интуит

Правильные ответы выделены зелёным цветом.
Все ответы: В курсе лекций излагаются основы теории вероятностей. Курс включает основы теории меры, основы комбинаторики, элементарную и аналитическую теорию вероятностей, предельные теоремы теории вероятностей.
Сколькими способами можно выбрать из полной колоды в 52 карты по одной карте каждой масти?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, у которых существует математическое ожидание.
(1) распределение с плотностью math
(2) распределение с плотностью math
(3) распределение с плотностью math
(4) распределение math
Случайные величины math и math независимы и имеют стандартное нормальное распределение. Укажите значение их коэффициента корреляции.
(1) -1
(2) 0
(3) 1
(4) 2
Выберите верные определения.
(1) math
(2) math
(3) math
(4) math
Выберите верные определения.
(1) math
(2) math
(3) math
(4) math
Что такое характеристическая функция случайной величины math?
(1) math
(2) math
(3) math
(4) math
Пусть math, math. Укажите верное высказывание.
(1) math
(2) math
(3) math
Пусть math. Какие из следующих множеств образуют алгебры подмножеств math?
(1) math
(2) math
(3) math
(4) math
Пусть P(B) > 0. Укажите, какая из следующих величин называется условной вероятностью события A при условии B.
(1) P(A ∩ B)/P(A)
(2) P(A ∩ B)/P(B)
(3) P(A)/P(B)
(4) P(B)/P(A ∩ B)
Правильную монету подбросили 14 раз, и выпали только гербы. С какой вероятностью при 15-м броске выпадет герб?
(1) 1/2
(2) 1/215
(3) 15/215
(4) 15!/215
Пусть math. Какие из следующих функций являются случайными величинами?
(1) math
(2) math
(3) math
(4) math
Бросают 10 симметричных игральных костей. Какое распределение имеет число костей, на которых выпало шесть очков?
(1) равномерное на отрезке от 1 до 10
(2) биномиальное с параметрами 10 и 1/6
(3) равномерное на отрезке от 10 до 60
(4) распределение Пуассона с параметром 6
Выберите свойства, которыми обладает любая функция совместного распределения.
(1) функция совместного распределения равна произведению частных функций распределения
(2) функция совместного распределения стремится к единице, если все переменные неограниченно возрастают
(3) функция совместного распределения стремится к единице, если одна из переменных неограниченно возрастает
(4) функция совместного распределения стремится к нулю, если одна из переменных неограниченно убывает
Пусть math. Укажите значение вероятности math.
(1) math
(2) math
(3) math
(4) math
В соревнованиях участвуют три лыжника. Сколькими способами они могут расположиться на трёх призовых местах?
(1) 12
(2) 3
(3) 6
(4) 27
Выберите распределения, у которых существует дисперсия.
(1) распределение с плотностью math
(2) распределение с плотностью math
(3) распределение с плотностью math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если случайные величины math и math независимы, то их коэффициент корреляции равен нулю
(2) модуль коэффициента корреляции случайных величин math и math равен единице
(3) модуль ковариации случайных величин math и math не превосходит единицы
(4) math
Дана последовательность случайных величин math со следующими распределениями: для любого math math Найдите предел последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) +∞
(4) 1/2
Дана последовательность случайных величин math со следующими распределениями: math. Если последовательность math слабо сходится к некоторому распределению, найдите это распределение.
(1) math
(2) math
(3) math
(4) последовательность не сходится по распределению
Укажите значение характеристической функции в точке math.
(1) 0
(2) 1
(3) math
(4) math
Подбрасывают две одинаковые игральные кости. Каково общее число равновозможных элементарных исходов?
(1) 2
(2) 12
(3) 21
(4) 36
Пусть math — произвольное непустое множество. Укажите верные высказывания.
(1) всякая алгебра является σ-алгеброй
(2) math является сигма-алгеброй
(3) всякая σ-алгебра является алгеброй
(4) алгебра всегда содержит лишь конечное число множеств
Пусть события A и B независимы, P(A) = 0, 4, P(B) = 0, 6. Выберите верное высказывание.
(1) P(A ∩ B) < P(A|B) < P(A ∪ B) < P(A)
(2) P(A|B) < P(A ∩ B) < P(A) < P(A ∪ B)
(3) P(A ∩ B) < P(A|B) < P(A) < P(A ∪ B)
(4) P(A) < P(A ∩ B) < P(A|B) < P(A ∪ B)
Пять раз подбрасывают правильную монету. Выберите верные высказывания.
(1) пять раз выпадет герб с вероятностью 1/32
(2) при первых трех бросках выпадут гербы с вероятностью 1/8
(3) один герб и четыре решки выпадут с вероятностью 1/32
(4) два герба и три решки выпадут с вероятностью 5/16
Выберите верные утверждения.
(1) если распределения двух случайных величин совпадают, то эти случайные величины совпадают
(2) распределение случайной величины может не существовать
(3) зная распределение случайной величины math, можно найти вероятность math
(4) распределение полностью определяется функцией распределения
Случайная величина math имеет равномерное распределение на отрезке [0, 5]. Вычислите следующие вероятности и укажите верные равенства.
(1) math
(2) math
(3) math
(4) math
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-1012
00, 10, 2500
100, 2p0, 1
200, 100, 1
Выберите верные высказывания.
(1) math
(2) math и math независимы
(3) math
(4) math
Случайная величина math имеет абсолютно непрерывное распределение с плотностью math. Пусть math. Какова плотность распределения случайной величины math?
(1) math
(2) math
(3) math
(4) math
Сколькими способами можно составить очередь к зубному врачу из 20 школьников одного класса?
(1) math
(2) math
(3) math
(4) 20
(5) 1
Выберите верные утверждения.
(1) возможно, что существует math, но не существует math
(2) если случайная величина п. н. ограничена, то ее математическое ожидание существует
(3) возможно, что математическое ожидание случайной величины существует, а дисперсия — нет
(4) возможно, что дисперсия случайной величины существует, а математическое ожидание — нет
Случайные величины math и math независимы и имеют стандартное нормальное распределение. Найдите коэффициент корреляции случайных величин math.
(1) math
(2) 0
(3) math
(4) math
(5) math
Дана последовательность случайных величин math. Выберите достаточные условия для сходимости math.
(1) math
(2) math
(3) math
(4) math
Дана последовательность независимых и одинаково распределенных случайных величин с показательным распределением с параметром math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите распределение, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
В урне 3 белых и 4 черных шара. Из урны наудачу вынимают один шар. Какова вероятность того, что он окажется черным?
(1) 3/4
(2) 4/3
(3) 4/7
(4) 1/2
Пусть math — произвольное непустое множество, math — некоторое непустое множество его подмножеств, содержащее вместе с любым своим элементом math. Выберите условия, при выполнении которых множество math будет σ-алгеброй.
(1) math
(2) math
(3) math
В урне 1 белый шар и 2 черных. Два игрока поочередно вынимают из урны по шару, не возвращая их обратно. Выигрывает тот, кто раньше достанет белый шар. Какова вероятность того, что выиграет 2-й игрок?
(1) 1/4
(2) 1/3
(3) 1/2
(4) 2/3
Какая формула вычисляет вероятность получить ровно три попадания при пяти выстрелах, если вероятность попадания в каждом равна 0,9 и результаты выстрелов независимы?
(1) 3 · 0,93 · 0,12
(2) 0,93 · 0,12
(3) 10 · 0,93 · 0,12
(4) 3/5
Пусть задано вероятностное пространство — отрезок [0, 1] с сигма алгеброй борелевских подмножеств и мерой Лебега в качестве вероятности. Укажите тип распределения случайной величины math, заданной равенством: math
(1) дискретное распределение
(2) абсолютно непрерывное распределение
(3) сингулярное распределение
(4) смешанное распределение
Из урны, содержащей два белых и три черных шара, наугад вынимают сразу три шара. Случайная величина math равна числу белых шаров среди выбранных. Вычислите следующие вероятности и укажите верное неравенство.
(1) math
(2) math
(3) math
(4) math
Бросают две симметричные игральные кости. Случайная величина math равна сумме выпавших очков, случайная величина math равна числу выпавших единиц. Укажите вероятность события math.
(1) 1/12
(2) 1/18
(3) 1/36
(4) 5/36
(5) 125/1296
Пусть math. Укажите значение плотности распределения случайной величины math в точке math.
(1) math
(2) math
(3) math
(4) math
Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Найдите math, если случайная величина math имеет распределение с плотностью math
(1) e1/3
(2) 3/2
(3) 1
(4) 1/3
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-505
00, 10, 20, 3
500, 20, 2
Найдите ковариацию случайных величин math и math.
(1) 0
(2) -1
(3) 1
(4) 1/2
(5) 2
Пусть math. Оценивается сверху вероятность math. Укажите значение оценки по неравенству Маркова.
(1) 0, 1
(2) 0, 05
(3) 0, 06
(4) 1
Дана последовательность независимых и одинаково распределенных случайных величин с показательным распределением с параметром math, math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите математическое ожидание и дисперсию распределения, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Из колоды в 36 карт наудачу выбирают две карты. Какова вероятность того, что они обе окажутся картами масти пик?
(1) 1/4
(2) 1/18
(3) 2/35
(4) 1/16
Пусть math. Выберите функции, которые являются мерами.
(1) math
(2) math
(3) math
(4) math
События A и B называются независимыми, если...
(1) вероятность их объединения равна сумме их вероятностей
(2) вероятность их пересечения равна сумме их вероятностей
(3) вероятность их объединения равна произведению их вероятностей
(4) вероятность их пересечения равна произведению их вероятностей
Стрелок попадает в цель при любом выстреле с вероятностью 0,3. Результаты выстрелов независимы. Какова вероятность того, что первое попадание случится только при пятом выстреле?
(1) 0,74
(2) 0,3
(3) 5 · 0,74 · 0,3
(4) 0,74 · 0,3
Пусть случайная величина math принимает только значения math с одинаковой вероятностью math. Найдите math.
(1) 0
(2) 0,2
(3) 0,25
(4) 1
Случайная величина math имеет нормальное распределение с плотностью распределения math. Укажите, какая из следующих случайных величин имеет стандартное нормальное распределение.
(1) math
(2) math
(3) math
(4) math
Пусть случайный вектор math имеет абсолютно непрерывное распределение. Если в некоторой области функция распределения этого вектора равна math, то какова его плотность распределения в той же области?
(1) 1
(2) 8
(3) 0
(4) math
Пусть math. Укажите распределение случайной величины math.
(1) math
(2) math
(3) math
(4) math
Брошены три монеты. Рассматриваются события math и math. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Найдите math, если случайная величина math имеет распределение Пуассона с параметром math.
(1) 4
(2) e2
(3) 2e
(4) 2
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) math тогда и только тогда, когда случайные величины math и math независимы
(2) math тогда и только тогда, когда случайные величины math и math некоррелированы
(3) величины math отрицательно коррелированы
(4) math
Пусть math. Укажите, каким числом оценивется по неравенству Чебышева вероятность math.
(1) 1/3
(2) 1/9
(3) 1
(4) 1/27
Правильная монета подбрасывается 6400 раз. Используя ЦПТ, найдите приближенно вероятность того, что число гербов будет отличаться от 3200 не менее, чем на 40.
(1) math
(2) math
(3) math
(4) math
(5) math
Случайные величины math и math независимы. Чему равна характеристическая функция их суммы?
(1) сумме характеристических функций
(2) разности характеристических функций
(3) произведению характеристических функций
(4) частному характеристических функций
В списке студенческой группы 5 юношей и 2 девушки. Из списка группы наугад выбирают троих студентов. Какова вероятность того, что будут выбраны два юноши и одна девушка?
(1) 2/7
(2) 4/7
(3) 1/3
(4) 1/7
Укажите множества, принадлежащие борелевской сигма-алгебре math.
(1) [-3, 3]
(2) (-3, 3)
(3) (-∞, 7]
(4) {3}
Выберите верные утверждения.
(1) противоположные друг другу события несовместны
(2) противоположные события независимы
(3) противоположные события зависимы
(4) достоверное событие независимо с любым другим
На отрезок [0, 1] наудачу и независимо друг от друга бросают пять точек. Какова вероятность того, что две из них попадут на левую половину отрезка, еще две — на отрезок [0,5, 0,7] и одна окажется правее точки 0,7?
(1) 0,09
(2) 0,003
(3) 0,36
(4) 0,9
Пусть распределение случайной величины math задано таблицей распределения:
ai-1012
P(ξ = ai)1/3p1/3p
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите дискретные распределения.
(1) бернулли
(2) геометрическое
(3) равномерное на отрезке
(4) нормальное
(5) пуассона
(6) гамма
Пусть независимые случайные величины math и math имеют абсолютно непрерывные распределения. Выберите верные утверждения.
(1) функция их совместного распределения равна сумме их функций распределения
(2) плотность их совместного распределения равна произведению плотностей их распределений
(3) функция их совместного распределения равна произведению их функций распределения
(4) плотность их совместного распределения равна сумме плотностей их распределений
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены math монет. При каждом math рассматривается событие math — на math-й монете выпал герб. Выберите верное высказывание.
(1) math
(2) math
(3) math
(4) math
В приборе имеются три ненадежных элемента, вероятности отказа которых равны соответственно 0,3, 0,6 и 0,5. Найдите математическое ожидание числа элементов, отказавших за время эксперимента.
(1) 0,09
(2) 1,4
(3) 1
(4) 2
(5) 3
Точка с координатами math и math наудачу выбрана в квадрате math. Найдите коэффициент корреляции координат точки и выберите верные утверждения.
(1) math и math независимы
(2) math и math зависимы
(3) math
(4) math
Пусть math — последовательность независимых случайных величин с одним и тем же распределением Бернулли с параметром math. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1/4
(3) 1/2
(4) 3/4
(5) предела не существует или указанных условий недостаточно
Имеется последовательность независимых и одинаково распределенных случайных величин. Укажите, при каких распределениях членов последовательности эта последовательность удовлетворяет центральной предельной теореме.
(1) распределение Пуассона с параметром 2
(2) показательное распределение с параметром 2
(3) распределение Коши с параметрами 0 и 1
(4) распределение с плотностью math при math
Укажите верные высказывания.
(1) если характеристические функции двух случайных величин совпадают, то эти случайные величины совпадают
(2) если характеристические функции двух случайных величин совпадают, то распределения этих случайных величин совпадают
(3) двум разным распределениям могут отвечать одинаковые характеристические функции
(4) по характеристической функции однозначно определяется распределение
Из букв слова БОЛТ, составленного с помощью разрезной азбуки, извлекают наудачу и выкладывают в порядке извлечения три буквы. Какова вероятность того, что при этом получится слово ЛОТ?
(1) 3/4
(2) 1/24
(3) 1/64
(4) 1/12
Пусть math и math — произвольные события, причем math влечет math. Выберите верное высказывание:
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) события, образующие полную группу, независимы
(2) события, образующие полную группу, несовместны
(3) несовместные события зависимы
(4) достоверное событие независимо с любым другим
Прибор состоит из 1000 независимо работающих элементов. Вероятность отказа любого из них при включении равна 0,001. По теореме Пуассона найдите приближенно вероятность того, что откажут ровно 2 элемента.
(1) 0,002
(2) 0,184
(3) 0,271
(4) 0,368
Какие из следующих функций являются плотностями распределений?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, для которых вероятность math является наибольшей среди перечисленных.
(1) math
(2) math
(3) math
(4) math
Пусть math и math — независимые случайные величины, равномерно распределенные на отрезке [0, 1]. Укажите, чему равна вероятность события math.
(1) 0,1
(2) 0,2
(3) 0,5
(4) 0,7
К случайной величине, имеющей абсолютно непрерывное распределение, прибавили 5. Выберите верные высказывания.
(1) тогда график ее плотности сдвинется влево на 5
(2) тогда график ее плотности сдвинется вправо на 5
(3) тогда график ее функции распределения сдвинется влево на 5
(4) тогда график ее функции распределения сдвинется вправо на 5
Событие math состоит в том, что первая деталь дефектна, событие math — вторая деталь дефектна. Какие из следующих событий означают, что ровно одна из этих двух деталей дефектна?
(1) math
(2) math
(3) math
(4) math
Случайные величины math независимы. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Подбрасывают правильную игральную кость. После math подбрасываний обозначим через math количество подбрасываний, при которых выпало 3 очка. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 1/2
(2) 0
(3) 1/6
(4) 1/4
(5) предела не существует
После бури на участке между 40-м и 65-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии?
(1) 0,25
(2) 0,2
(3) 0,75
(4) 0,5
Вероятность получить "отлично" по математике равна 1/4, по физике — тоже 1/4, а сразу по двум предметам — 1/8. Какова вероятность получить "отлично" хотя бы по одному предмету?
(1) 1/16
(2) 3/8
(3) 1/2
(4) 7/8
На фабрике половина продукции производится первой машиной, половина — второй. Первая машина дает 10% брака, вторая — 20%. Определите вероятность наугад выбранной детали оказаться бракованной.
(1) 0, 05
(2) 0, 15
(3) 0, 3
(4) 0, 5
Проводится math испытаний схемы Бернулли с вероятностью успеха math. Укажите, при каких значениях math и math можно использовать теорему Пуассона для приближенного вычисления вероятностей, если погрешность приближения не должна превышать 0,005.
(1) math
(2) math
(3) math
(4) math
Пусть распределение случайной величины math задано плотностью распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Укажите распределение суммы двух независимых случайных величин math.
(1) math
(2) math
(3) math
(4) math
Подброшены три монеты. Событие math означает, что на первой монете выпал герб, а на остальных двух — решки, событие math означает, что выпал хотя бы один герб, событие math — выпал ровно один герб. Укажите верное отношение.
(1) math
(2) math
(3) math
(4) math
(5) math
(6) math
Пусть math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Пусть math — последовательность независимых случайных величин с одним и тем же распределением Бернулли с параметром math. Укажите, чему равен предел при math последовательности math в смысле сходимости почти наверное.
(1) 0
(2) 1/4
(3) 1/2
(4) 3/16
(5) 1/16
Внутри круга с радиусом 2 см лежат, не перекрываясь, две одинаковые монеты с радиусом 1 см. Какова вероятность того, что наудачу брошенная в круг точка упадет на одну из монет?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Укажите равенство, верное для любой последовательности событий math
(1) math
(2) math
(3) math
(4) math
На фабрике половина продукции производится первой машиной, половина — второй. В продукции первой машины брак составляет 10%, в продукции второй — 30%. Наугад выбранная из всей продукции деталь оказалась бракованной. Какова вероятность того, что эта деталь изготовлена первой машиной?
(1) 0, 25
(2) 0, 35
(3) 0, 5
(4) 0, 6
Пусть распределение случайной величины math задано функцией распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Даны пять независимых в совокупности случайных величин math с одним и тем же распределением Пуассона с параметром 2. Найдите math.
(1) math
(2) 0
(3) math
(4) math
Укажите, в какой последовательности распределений математические ожидания упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,3,1,4
(4) 4,3,1,2
(5) 3,2,1,4
Выберите последовательности случайных величин, удовлетворяющие закону больших чисел.
(1) случайные величины независимы и имеют показательное распределение с одним и тем же параметром
(2) случайные величины независимы и имеют показательные распределения с разными параметрами, math
(3) случайные величины совпадают, т. е. math, и имеют показательное распределение
(4) случайные величины независимы, math
Точка с координатой math наудачу бросается на отрезок math. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Подбрасывают три игральных кости. Выберите набор событий, для которого вероятность объединения равняется сумме вероятностей событий из набора.
(1) math
(2) math
(3) math
Пусть распределение случайной величины math абсолютно непрерывно, math — функция распределения случайной величины math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) плотность распределения суммы любых случайных величин с абсолютно непрерывными распределениями равна свертке их плотностей
(2) плотность распределения суммы независимых случайных величин с абсолютно непрерывными распределениями равна сумме их плотностей
(3) сумма независимых случайных величин с равномерными распределениями имеет равномерное распределение
(4) сумма независимых случайных величин с нормальными распределениями имеет нормальное распределение
Укажите, в какой последовательности распределений дисперсии упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,1,3,4
(4) 4,3,1,2
(5) 3,1,2,4
Считая, что math п. н. и указанные математические ожидания существуют, выберите верные неравенства.
(1) math
(2) math
(3) math
(4) math
Нужно отправить пять писем. Сколькими способами это можно сделать, если есть два курьера, и каждое из писем можно вручить любому курьеру?
(1) 32
(2) 10
(3) 20
(4) 25
Выберите распределения, у которых существует математическое ожидание.
(1) распределение с плотностью math
(2) распределение с плотностью math
(3) распределение с плотностью math
(4) распределение math
Случайные величины math и math независимы и имеют одно и то же распределение Пуассона с параметром math. Укажите значение их коэффициента корреляции.
(1) 0
(2) -1
(3) 1
(4) 2
Выберите верные определения.
(1) math
(2) math
(3) math
(4) math
Отметьте верное утверждение.
(1) math
(2) math
(3) math
(4) math
Случайная величина math принимает значения ±1 с вероятностями по 1/2. Найдите характеристическую функцию math.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Пусть math. Какие из следующих множеств образуют алгебры подмножеств math?
(1) math
(2) math
(3) math
(4) math
Пусть P(A) > 0, B — произвольное событие. Укажите верные высказывания.
(1) P(A ∩ B) = P(A)P(B)
(2) P(A ∩ B) = P(A)P(B |A)
(3) P(A ∩ B) = P(A) + P(B |A)
(4) P(A ∩ B) = P(A) + P(B)
Симметричную игральную кость бросали 29 раз, и ни разу не выпало шесть очков. С какой вероятностью при 30-м броске снова не выпадет шесть очков?
(1) math
(2) math
(3) math
(4) math
Пусть math. Какие из следующих функций являются случайными величинами?
(1) math
(2) math
(3) math
Правильную монету бросают 10 раз. Какое распределение имеет число выпавших гербов?
(1) стандартное нормальное
(2) равномерное на отрезке от 0 до 10
(3) биномиальное с параметрами 10 и 0,5
(4) распределение Пуассона с параметром 5
Выберите свойства, которыми обладает любая функция совместного распределения.
(1) зная функцию совместного распределения, можно найти частные функции распределения
(2) функция совместного распределения не убывает по каждой переменной
(3) функция совместного распределения непрерывна по каждой переменной
(4) зная частные распределения, можно найти функцию совместного распределения
Пусть math. Укажите значение вероятности math.
(1) 1/32
(2) 1/8
(3) 1/6
(4) 1/4
В футбольном турнире участвуют четыре команды. Сколькими способами можно выбрать из них пару команд для первого матча?
(1) 12
(2) 3
(3) 6
(4) 27
Выберите распределения, у которых существует дисперсия.
(1) распределение с плотностью math
(2) распределение с плотностью math
(3) распределение с плотностью math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если коэффициент корреляции случайных величин math и math равен нулю, то они независимы
(2) модуль коэффициента корреляции случайных величин math и math не превосходит единицы
(3) если ковариация случайных величин math и math равна единице, то они зависимы
(4) math
Дана последовательность случайных величин math со следующими распределениями: для любого math math Найдите предел последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) 2
(4) -2
Дана последовательность случайных величин math со следующими распределениями: math Если последовательность math слабо сходится к некоторому распределению, найдите это распределение.
(1) math
(2) math
(3) math
(4) последовательность не сходится по распределению
Укажите, чему равна характеристическая функция случайной величины math.
(1) math
(2) math
(3) math
(4) math
Карточки с буквами А, Б, В, Г выкладывают в ряд в произвольном порядке. Каково общее число равновозможных элементарных исходов?
(1) 1
(2) 4
(3) 16
(4) 24
Пусть math — произвольное непустое множество. Укажите верные высказывания.
(1) существуют алгебры, не являющиеся math-алгебрами
(2) math является алгеброй
(3) существуют math- алгебры, не являющиеся алгебрами
(4) math-алгебра всегда содержит бесконечное число множеств
Пусть события A и B независимы, P(A) = 0,8, P(B) = 0,4. Выберите верное высказывание.
(1) P(A ∩ B) < P(A|B) < P(A ∪ B) < P(A)
(2) P(A|B) < P(A ∩ B) < P(A) < P(A ∪ B)
(3) P(A ∩ B) < P(A|B) < P(A) < P(A ∪ B)
(4) P(A) < P(A ∩ B) < P(A|B) < P(A ∪ B)
Стрелок, попадающий в цель при одном выстреле с вероятностью 0,3, делает два выстрела. Результаты выстрелов независимы. Выберите верное высказывание.
(1) вероятность попасть ровно один раз равна 0,3
(2) вероятность попасть дважды равна 0,6
(3) вероятность попасть при втором выстреле, если при первом был промах, равна 0,21
(4) вероятность попасть ровно один раз равна 0,42
Выберите верные утверждения:
(1) функция распределения сингулярного распределения всюду непрерывна
(2) функция распределения случайной величины может не существовать
(3) у любого распределения существует плотность распределения
(4) случайная величина с дискретным распределением принимает только целые значения
Случайная величина math имеет равномерное распределение на отрезке [-2, 2]. Вычислите следующие вероятности и укажите верные неравенства.
(1) math
(2) math
(3) math
(4) math
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-1012
00, 10, 2500
100, 2p0, 1
200, 100, 1
Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Случайная величина math имеет абсолютно непрерывное распределение с плотностью math. Пусть math. Какова плотность распределения случайной величины math?
(1) math
(2) math
(3) math
(4) math
Четыре раза подбрасывают шестигранную игральную кость и записывают количество выпадающих очков в порядке поступления. Сколько различных двузначных чисел можно таким образом записать?
(1) math
(2) math
(3) math
(4) math
(5) math
Выберите верные утверждения.
(1) math существует тогда и только тогда, когда math
(2) если случайная величина может принимать сколь угодно большие значения, то ее математическое ожидание не существует
(3) если существует математическое ожидание случайной величины, то существует и дисперсия
(4) математическое ожидание всегда неотрицательно
Случайные величины math и math независимы и имеют одно и то же распределение Пуассона с параметром 2. Найдите коэффициент корреляции случайных величин math.
(1) math
(2) 0
(3) math
(4) math
(5) math
Дана последовательность случайных величин math. Выберите достаточные условия для сходимости math.
(1) math
(2) math
(3) math
(4) math
Дана последовательность независимых и одинаково распределенных случайных величин с равномерным распределением на отрезке [-1, 1], math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите распределение, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Один раз подбрасывают симметричную игральную кость. Какова вероятность того, что выпадет одно или два очка?
(1) 1/3
(2) 1/2
(3) 1/6
(4) 2/3
Пусть math — произвольное непустое множество, math — некоторое непустое множество его подмножеств, содержащее вместе с любым своим элементом math. Выберите условия, при выполнении которых множество math будет алгеброй.
(1) math
(2) math
(3) math
(4) math
В урне 1 белый шар и 2 черных. Два игрока поочередно вынимают из урны по шару, не возвращая их обратно. Выигрывает тот, кто раньше достанет белый шар. Какова вероятность того, что выиграет 1-й игрок?
(1) 1/4
(2) 1/3
(3) 1/2
(4) 2/3
Какая формула вычисляет вероятность получить ровно семь попаданий при восьми выстрелах, если вероятность попадания в каждом равна 0,9 и результаты выстрелов независимы?
(1) 0,97 · 0,1
(2) 8 · 0,97 · 0,1
(3) 7 · 0,97 · 0,1
(4) 1 - 0,98
Пусть задано вероятностное пространство — отрезок [0, 1] с сигмаалгеброй борелевских подмножеств и мерой Лебега в качестве вероятности. Укажите тип распределения случайной величины math, заданной равенством: math
(1) дискретное распределение
(2) абсолютно непрерывное распределение
(3) сингулярное распределение
(4) смешанное распределение
Из урны, содержащей два белых и три черных шара, наугад вынимают сразу три шара. Случайная величина math равна числу черных шаров среди выбранных. Вычислите следующие вероятности и укажите верное неравенство.
(1) math
(2) math
(3) math
(4) math
Бросают две симметричные игральные кости. Случайная величина math равна сумме выпавших очков, случайная величина math равна числу выпавших единиц. Укажите вероятность события math.
(1) 1/12
(2) 1/18
(3) 1/36
(4) 5/36
(5) 5/324
Пусть math. Укажите значение плотности распределения случайной величины math в точке math.
(1) math
(2) math
(3) math
(4) 0
Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Найдите math, если случайная величина math имеет распределение с плотностью math
(1) 1/2
(2) 3/4
(3) 27/64
(4) 1
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-505
00, 10, 20, 3
1000, 20, 2
Найдите ковариацию случайных величин math и math.
(1) 0
(2) -1
(3) 1
(4) 1/2
(5) 2
Пусть math. Оценивается сверху вероятность math. Укажите значение оценки по неравенству Чебышева.
(1) 0, 1
(2) 0, 05
(3) 0, 06
(4) 1
Дана последовательность независимых и одинаково распределенных случайных величин с равномерным распределением на отрезке math, math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите математическое ожидание и дисперсию распределения, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Из колоды в 36 карт наудачу выбирают две карты. Какова вероятность того, что ровно одна из них будет иметь пиковую масть?
(1) 27/70
(2) 27/140
(3) 3/8
(4) 3/4
Пусть math. Выберите функции, которые являются мерами.
(1) math
(2) math
(3) math
(4) math
Из колоды, состоящей из 36 карт, наугад выбрали одну карту. Укажите верные высказывания.
(1) события "выбрана пиковая карта" и "выбрана бубновая карта" несовместны
(2) события "выбрана дама" и "выбран король" независимы
(3) события "выбрана пиковая карта" и "выбран король" независимы
(4) события "выбрана пиковая карта" и "выбран туз" несовместны
Стрелок попадает в цель при любом выстреле с вероятностью 0,3. Результаты выстрелов независимы. Какова вероятность того, что первое попадание случится не ранее, чем при пятом выстреле?
(1) 0,74
(2) 0,3
(3) 5 · 0,74 · 0,3
(4) 0,74 · 0,3
Пусть случайная величина math принимает только значения math с одинаковой вероятностью math. Найдите math.
(1) 0
(2) 0,2
(3) 0,25
(4) 1
Случайная величина math имеет нормальное распределение с плотностью распределения math. Укажите, какая из следующих случайных величин имеет стандартное нормальное распределение.
(1) math
(2) math
(3) math
(4) math
Пусть случайный вектор math имеет абсолютно непрерывное распределение. Если в некоторой области функция распределения этого вектора равна math, то какова его плотность распределения в той же области?
(1) math
(2) 0
(3) 1
(4) 3
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены три монеты. Рассматриваются события math — на первой монете выпал герб, math. Выберите верное высказывание.
(1) math
(2) math
(3) math
(4) math
Найдите math, если случайная величина math принимает только целые значения от 0 до 4 с равными вероятностями.
(1) 20
(2) 8
(3) 4/5
(4) 2/25
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если случайные величины math и math независимы, то math
(2) если math, то случайные величины math и math некоррелированы
(3) величины math отрицательно коррелированы
(4) math
Пусть math. Укажите, каким числом оценивется по неравенству Чебышева вероятность math.
(1) 0, 1
(2) 1
(3) 0, 01
(4) 0, 001
Правильная монета подбрасывается 6400 раз. Используя ЦПТ, найдите приближенно вероятность того, что число гербов будет отличаться от 3200 не менее, чем на 100.
(1) math
(2) math
(3) math
(4) math
(5) math
Если момент пятого порядка случайной величины math существует, что можно сказать про ее характеристическую функцию?
(1) она равна 0 в точке math
(2) она имеет непрерывную производную пятого порядка
(3) math
(4) она равна 5 в точке math
В списке студенческой группы 5 юношей и 2 девушки. Из списка группы наугад выбирают троих студентов. Какова вероятность того, что будут выбраны только юноши?
(1) 2/7
(2) 4/7
(3) 1/3
(4) 1/7
Пусть math, и сигма-алгебра math содержит множество всех открытых интервалов на числовой прямой. Укажите множества, принадлежащие math.
(1) [-3, 3]
(2) [3, +∞)
(3) (-∞, 7]
(4) {3}
Выберите верные утверждения.
(1) несовместные события не пересекаются
(2) невозможное событие независимо с любым другим
(3) несовместные события независимы
(4) несовместные события зависимы
Симметричную игральную кость подбрасывают 4 раза. Какова вероятность получить при этом одну тройку и две шестерки?
(1) 1/216
(2) 1/324
(3) 1/27
(4) 1/36
Пусть распределение случайной величины math задано таблицей распределения:
ai-1012
P(math = ai)1/3p1/3p
Выберите верное утверждение.
(1) math
(2) math
(3) math
(4) math
Выберите абсолютно непрерывные распределения.
(1) бернулли
(2) геометрическое
(3) равномерное на отрезке
(4) нормальное
(5) пуассона
(6) гамма
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены math монет. При каждом math рассматривается событие math — на math-й монете выпал герб. Какие из следующих событий состоят в том, что выпала хотя бы одна решка?
(1) math
(2) math
(3) math
(4) math
В приборе имеются четыре ненадежных элемента, вероятности отказа которых равны соответственно 0,2, 0,3, 0,6 и 0,5. Найдите математическое ожидание числа отказавших элементов.
(1) 0,018
(2) 1,6
(3) 1
(4) 2
(5) 3
Точка с координатами math и math наудачу выбрана в ромбе {(x, y) | |x|+|y| ≤ 1}. Найдите коэффициент корреляции координат точки и выберите верные утверждения.
(1) math и math независимы
(2) math и math зависимы
(3) math
(4) math
Пусть math — последовательность независимых случайных величин с одним и тем же показательным распределением с параметром math. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1/4
(3) 1/2
(4) 2
(5) предела не существует или указанных условий недостаточно
Имеется последовательность независимых и одинаково распределенных случайных величин. Укажите, при каких распределениях членов последовательности эта последовательность удовлетворяет центральной предельной теореме.
(1) распределение Бернулли с параметром 1/2
(2) показательное распределение с параметром 1
(3) вырожденное распределение в точке 2
(4) распределение с плотностью math при math
Укажите верные высказывания.
(1) если характеристические функции двух случайных величин совпадают, то функции распределения этих случайных величин совпадают
(2) если модуль характеристической функции интегрируем на всей прямой, то распределение абсолютно непрерывно
(3) характеристическая функция суммы двух случайных величин равна произведению их характеристических функций
(4) если характеристическая функция тождественно равна единице, то распределение вырождено в нуле
Из букв слова ЛОТО, составленного с помощью разрезной азбуки, извлекают наудачу и выкладывают в порядке извлечения три буквы. Какова вероятность того, что при этом получится слово ЛОТ?
(1) 3/4
(2) 1/24
(3) 1/64
(4) 1/12
Выберите свойства, верные для любых несовместных событий math и math.
(1) math
(2) math
(3) math
(4) math
Один раз бросают правильную монету. Выберите верные утверждения.
(1) события "выпал герб" и "выпала решка" несовместны
(2) события "выпал герб" и "выпала решка" независимы
(3) события "выпал герб" и "выпала решка" образуют полную группу событий
(4) события "выпал герб" и "выпала решка" противоположны
Прибор состоит из 1000 независимо работающих элементов. Вероятность отказа любого из них при включении равна 0,001. По теореме Пуассона найдите приближенно вероятность того, что откажет ровно 1 элемент.
(1) 0,002
(2) 0,184
(3) 0,271
(4) 0,368
Какие из следующих функций являются плотностями распределений?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, для которых вероятность math является наибольшей среди перечисленных.
(1) math
(2) math
(3) math
(4) math
Пусть math и math — независимые случайные величины. Укажите, чему равна вероятность события math.
(1) 0,1
(2) 0,2
(3) 0,4
(4) 0,9
От случайной величины, имеющей абсолютно непрерывное распределение, отняли 5. Выберите верные высказывания.
(1) тогда график ее плотности сдвинется влево на 5
(2) тогда график ее плотности сдвинется вправо на 5
(3) тогда график ее функции распределения сдвинется влево на 5
(4) тогда график ее функции распределения сдвинется вправо на 5
Пусть math. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Случайные величины math независимы. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Подбрасывают две правильные монеты. После math подбрасываний пары монет обозначим через math количество подбрасываний, при которых выпало два герба. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 1/2
(2) 0
(3) 1/6
(4) 1/4
(5) предела не существует
В точке math, положение которой на телефонной линии math длиной 100 км равновозможно, произошел разрыв линии. Какова вероятность того, что точка math удалена от точки math не более, чем на 25 км?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Бросают две правильные игральные кости. Какова вероятность получить нечетное число очков хотя бы на одной кости?
(1) 0,25
(2) 0,5
(3) 0,75
(4) 1
Половина стрелков попадает в цель в 60% случаев, половина — в 80% случаев. Выбранный случайным образом стрелок произвел выстрел. Определите вероятность попадания в цель.
(1) 0, 3
(2) 0, 5
(3) 0, 7
(4) 1, 4
Проводится math испытаний схемы Бернулли с вероятностью успеха math. Укажите, при каких значениях math и math можно использовать теорему Пуассона для приближенного вычисления вероятностей, если погрешность приближения не должна превышать 0,001.
(1) math
(2) math
(3) math
(4) math
Пусть распределение случайной величины math задано плотностью распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Укажите распределение суммы двух независимых случайных величин math.
(1) math
(2) math
(3) math
(4) math
Три стрелка каждый по разу стреляют по мишени. Событие math означает, что попал хотя бы один из них, событие math означает, что попал только второй стрелок, событие math — произошло только одно попадание. Укажите верное отношение.
(1) math
(2) math
(3) math
(4) math
(5) math
(6) math
Пусть math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Пусть math — последовательность независимых случайных величин с одним и тем же показательным распределением с параметром math. Укажите, чему равен предел при math последовательности math в смысле сходимости почти наверное.
(1) 0
(2) 1/4
(3) 1/2
(4) 2
(5) 4
Внутри круга с радиусом 5 см лежат, не перекрываясь, пять одинаковых монет с радиусом 1 см. Какова вероятность того, что наудачу брошенная в круг точка упадет на одну из монет?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Пусть math обозначает меру Лебега борелевского множества math. Укажите значение math.
(1) 0
(2) 1
(3) 2
(4) 3
Первый стрелок попадает в цель в 90% случаев, второй — в 60% случаев. Выбранный случайным образом стрелок произвел выстрел и попал в мишень. Определите вероятность того, что это был второй стрелок.
(1) 0, 4
(2) 0, 5
(3) 0, 6
(4) 0, 75
Пусть распределение случайной величины math задано функцией распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите значение в точке math плотности распределения суммы трех независимых в совокупности случайных величин с одним и тем же нормальным распределением с параметрами math.
(1) math
(2) math
(3) 1/2
(4) math
Укажите, в какой последовательности распределений математические ожидания упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,3,1,4
(4) 4,3,1,2
(5) 3,2,1,4
Выберите последовательности случайных величин, удовлетворяющие закону больших чисел.
(1) случайные величины независимы и имеют стандартное нормальное распределение
(2) случайные величины независимы и имеют разные нормальные распределения, math
(3) случайные величины совпадают, т. е. math, и имеют распределение Бернулли с параметром math
(4) случайные величины независимы, math
Точка с координатами math и math наудачу бросается в квадрат math. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Подбрасывают две игральных кости. Укажите такие события math и math, для которых math.
(1) math
(2) math
(3) math
(4) math
Пусть math — произвольная функция распределения. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) плотность распределения суммы независимых случайных величин с абсолютно непрерывными распределениями равна свертке их плотностей
(2) сумма двух независимых случайных величин с дискретным и абсолютно непрерывным распределениями имеет абсолютно непрерывное распределение
(3) сумма независимых случайных величин с показательными распределениями имеет показательное распределение
(4) сумма независимых случайных величин с нормальными распределениями может иметь вырожденное распределение
Укажите, в какой последовательности распределений дисперсии упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,1,3,4
(4) 4,3,1,2
(5) 3,1,2,4
Считая, что math п. н. и указанные математические ожидания существуют, выберите верные неравенства.
(1) math
(2) math
(3) math
(4) math
На почте есть марки трёх видов, конверты четырёх видов и открытки пяти видов. Каким числом способов можно выбрать открытку, конверт и марку к нему?
(1) 3
(2) 220
(3) 12
(4) 60
Выберите распределения, у которых существует математическое ожидание.
(1) распределение с плотностью math
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии и связаны равенством math. Укажите значение их коэффициента корреляции.
(1) 0
(2) -1
(3) 1
(4) 2
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите функции, которые не могут быть характеристическими функциями никакой случайной величины.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите, какими могут быть вероятности элементарных исходов.
(1) 1/3, 1/3, 1/3
(2) 1/2, 1/2, 1/2
(3) 1/2, 0, 1/2
(4) 1, 0, 0
Пусть math. Какие из следующих множеств образуют алгебры подмножеств math?
(1) множество всех одноточечных подмножеств множества math
(2) множество всех интервалов math
(3) множество натуральных чисел
(4) множество всех подмножеств множества math
Пусть P(A) = 0, 2, P(B) = 0, 5, P(A ∩ B) = 0, 1. Найдите P(A|B).
(1) 0,1
(2) 0,2
(3) 0,4
(4) 0,7
Из урны, содержащей 10 одинаковых на ощупь шаров, среди которых один черный, наугад вынимали по одному шару 12 раз, всякий раз возвращая вынутый шар обратно и перемешивая шары в урне. Все 12 раз был вынут черный шар. С какой вероятностью следующий наудачу вынутый шар снова окажется черным?
(1) 0, 1
(2) (0, 1)12
(3) (0, 1)13
(4) 13 · (0, 1)13
Пусть math. Какие из следующих функций являются случайными величинами?
(1) math
(2) math
(3) math
(4) math
Точка наудачу выбирается на отрезке [0, 5]. Какое распределение имеет координата этой точки?
(1) нормальное с параметрами 0 и 5
(2) равномерное на отрезке от 0 до 5
(3) биномиальное с параметрами 5 и 0,5
(4) распределение Пуассона с параметром 5
Выберите верные высказывания.
(1) функция совместного распределения math равна вероятности math
(2) функция совместного распределения непрерывна слева по каждой переменной
(3) функция совместного распределения math равна вероятности math
(4) если случайные величины независимы, то, зная их частные распределения, можно найти функцию совместного распределения
Пусть math. Укажите значение вероятности math.
(1) 1/32
(2) 1/8
(3) 1/6
(4) 1/4
Сколькими способами можно выбрать из полной колоды в 52 карты четыре карты, если их порядок безразличен (карты не возвращаются в колоду)?
(1) math
(2) math
(3) math
(4) math
(5) 52
Выберите распределения, у которых существует дисперсия.
(1) распределение с плотностью math
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если ковариация случайных величин math и math равна нулю, то они независимы
(2) коэффициент корреляции случайных величин math и math принимает значения от 0 до 1
(3) если коэффициент корреляции случайных величин math и math равен 0,5, то они зависимы
(4) math
Дана последовательность случайных величин math со следующими распределениями: для любого math math Найдите предел последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) -1
(4) 1/n
Дана последовательность случайных величин math со следующими распределениями: math. Если последовательность math слабо сходится к некоторому распределению, найдите это распределение.
(1) math
(2) math
(3) math
(4) последовательность не сходится по распределению
Укажите, чему равна характеристическая функция случайной величины math.
(1) math
(2) math
(3) math
(4) math
Пусть math, а множество math содержит все конечные множества вещественных чисел (в том числе пустое) и их дополнения до math. Укажите верное высказывание.
(1) множество натуральных чисел принадлежит math
(2) math является σ-алгеброй
(3) math является алгеброй
(4) math
Пусть события A и B независимы, P(A) = 0, 2, P(B) = 0, 4. Выберите верное высказывание.
(1) P(A ∩ B) < P(A|B) < P(A ∪ B) < P(A)
(2) P(A|B) < P(A ∩ B) < P(A) < P(A ∪ B)
(3) P(A ∩ B) < P(A|B) < P(A) < P(A ∪ B)
(4) P(A) < P(A ∩ B) < P(A|B) < P(A ∪ B)
Трижды бросают правильную монету. Выберите верные высказывания.
(1) три решки выпадут с вероятностью 3/8
(2) один герб и две решки выпадут с вероятностью 3/8
(3) три герба выпадут с вероятностью 1/8
(4) одна решка и два герба выпадут с вероятностью 1/8
Выберите верное утверждение:
(1) сингулярное распределение может быть сосредоточено на множестве рациональных чисел
(2) math
(3) если math, то распределения случайных величин math и math совпадают
(4) плотность абсолютно непрерывного распределения в любой точке равна производной от функции распределения
Случайная величина math имеет биномиальное распределение с параметрами 3 и 1/3. Вычислите следующие вероятности и укажите верные равенства.
(1) math
(2) math
(3) math
(4) math
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-1012
00, 10, 2500
100, 2p0, 1
200, 100, 1
Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Случайная величина math имеет абсолютно непрерывное распределение с плотностью math. Пусть math. Какова плотность распределения случайной величины math?
(1) math
(2) math
(3) math
(4) math
Подбрасывают четыре неразличимых шестигранных игральных кости и записывают наборы выпадающих очков. Сколько различных наборов можно таким образом записать?
(1) math
(2) math
(3) math
(4) math
(5) math
Выберите верные утверждения.
(1) math для любых случайных величин с конечными математическими ожиданиями
(2) математическое ожидание постоянной равно нулю
(3) math для любых случайных величин с конечными математическими ожиданиями
(4) дисперсия всегда неотрицательна
Случайные величины math и math независимы и имеют одно и то же показательное распределение с параметром 2. Найдите коэффициент корреляции случайных величин math.
(1) math
(2) 0
(3) math
(4) math
(5) math
Дана последовательность случайных величин math. Выберите достаточные условия для сходимости math.
(1) math
(2) math
(3) math
(4) math
Дана последовательность независимых и одинаково распределенных случайных величин с биномиальным распределением с параметрами math. Пусть math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите распределение, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Есть 5 монет по 50 копеек и 3 монеты по рублю. Какова вероятность того, что выбранная наугад монета окажется монетой в один рубль?
(1) 5/8
(2) 3/5
(3) 1/2
(4) 3/8
Пусть math — произвольное непустое множество, math — алгебра его подмножеств, math — некоторые события. Укажите множества, принадлежащие math.
(1) math
(2) math
(3) math
(4) math
Из урны, содержащей 2 белых и 3 черных шара, вынимают шары по одному до тех пор, пока не появится белый шар. Какова вероятность того, что из урны будет вынуто 3 черных шара?
(1) 3/16
(2) 2/3
(3) 1/10
(4) 3/5
Какая формула вычисляет вероятность не получить ни одного попадания при пяти выстрелах, если вероятность попадания в каждом равна 0,9 и результаты выстрелов независимы?
(1) 0,15
(2) 0,95
(3) 1 - 0,95
(4) 1 - 0,15
Пусть задано вероятностное пространство — отрезок [0, 1] с сигма алгеброй борелевских подмножеств и мерой Лебега в качестве вероятности. Укажите тип распределения случайной величины math, заданной равенством: math
(1) дискретное распределение
(2) абсолютно непрерывное распределение
(3) сингулярное распределение
(4) смешанное распределение
Случайная величина math имеет распределение Пуассона с параметром 2. Вычислите следующие вероятности и укажите верное неравенство.
(1) math
(2) math
(3) math
(4) math
Бросают две симметричные игральные кости. Случайная величина math равна сумме выпавших очков, случайная величина math равна числу выпавших единиц. Укажите вероятность события math.
(1) 1/12
(2) 1/18
(3) 1/36
(4) 5/36
(5) 25/432
Пусть math. Укажите значение плотности распределения случайной величины math в точке math.
(1) 1
(2) 5
(3) 1/3
(4) 0
Пусть math и math — произвольные события. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Найдите math, если случайная величина math имеет распределение с плотностью math
(1) e-1/3
(2) 3/2
(3) 3/4
(4) -1/3
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-505
000, 20, 3
20, 10, 20, 2
Найдите ковариацию случайных величин math и math.
(1) 0
(2) -1
(3) 1
(4) 1/2
(5) 2
Пусть math. Оценивается сверху вероятность math. Укажите значение оценки по обобщенному неравенству Чебышева с функцией math.
(1) 0, 1
(2) 0, 05
(3) 0, 06
(4) 1
Дана последовательность независимых и одинаково распределенных случайных величин с биномиальным распределением с параметрами math. Пусть math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите математическое ожидание и дисперсию распределения, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Из колоды в 36 карт наудачу выбирают шесть карт. Какова вероятность того, что среди них окажется король пик?
(1) 1/6
(2) 1/36
(3) 1/9
(4) 1/4
Пусть math. Выберите функцию, которая является вероятностной мерой.
(1) math
(2) math
(3) math
(4) math
Пусть события A и B независимы, P(A) = 0,5, P(B) = 0,5. Укажите верные высказывания.
(1) события A и B противоположны
(2) P(A ∩ B) = 0,25
(3) P(A|B) = 0,5
Симметричную игральную кость бросают до тех пор, пока на кости впервые не выпадет четное число очков. Какова вероятность того, что придется бросить кость пять раз?
(1) 5/32
(2) 1/32
(3) 5/6
(4) 1/16
Пусть случайная величина math принимает только значения math с одинаковой вероятностью math. Найдите math.
(1) 0,2
(2) 0,4
(3) 0,6
(4) 1
Случайная величина math имеет нормальное распределение с плотностью распределения math. Пусть math — функция распределения стандартного нормального распределения. Чему равно значение вероятности math?
(1) math
(2) math
(3) math
(4) math
Пусть случайный вектор math имеет абсолютно непрерывное распределение с постоянной плотностью во всех точках круга math. Вне круга плотность нулевая. Каково значение плотности внутри круга?
(1) 1
(2) 1/2
(3) 1/2π
(4) 1/π
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены три монеты. Рассматриваются события math — на первой монете выпал герб, math — на второй монете выпал герб, math — выпал хотя бы один герб. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Найдите math, если случайная величина math имеет таблицу распределения math
(1) 1/4
(2) 4/3
(3) 1/2
(4) 1/3
Случайные величины math и math имеют конечные дисперсии. Укажите верные утверждения.
(1) если math, то случайные величины math и math независимы
(2) math
(3) величины math положительно коррелированы
(4) math
Пусть math. Укажите, каким числом оценивется по неравенству Чебышева вероятность math.
(1) 0, 01
(2) 0, 02
(3) 0, 04
(4) 0, 005
Правильная монета подбрасывается 6400 раз. Используя ЦПТ, найдите приближенно вероятность того, что число гербов будет отличаться от 3200 не менее, чем на 60.
(1) math
(2) math
(3) math
(4) math
(5) math
Если математическое ожидание случайной величины math равно нулю, а дисперсия равна единице, как выглядит разложение ее характеристической функции в ряд Тейлора в окрестности нуля?
(1) math
(2) math
(3) math
(4) math
В списке студенческой группы 5 юношей и 2 девушки. Из списка группы наугад выбирают троих студентов. Какова вероятность того, что будут выбраны один юноша и две девушки?
(1) 2/7
(2) 4/7
(3) 1/3
(4) 1/7
Укажите множества, принадлежащие борелевской сигма-алгебре math.
(1) множество натуральных чисел
(2) множество целых чисел
(3) множество рациональных чисел
(4) множество комплексных чисел
Пусть события A и B независимы, P(A) = 0, 5, P(B) = 0, 5. Укажите верные высказывания.
(1) события A и B совместны
(2) P(A ∪ B) = P(A) + P(B)
(3) P(A ∩ B) = P(A)P(B)
(4) P(A|B) = P(A)
Монета умеет с равными вероятностями выпадать гербом, решкой и вставать на ребро. Какова вероятность того, что при семи подбрасываниях этой монеты она трижды встанет на ребро и два раза выпадет решкой?
(1) 1/37
(2) 210/37
(3) 7!/37
(4) 7/37
Пусть распределение случайной величины math задано таблицей распределения:
ai-2-101
P(ξ = ai)pp0, 250, 5
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите дискретные распределения.
(1) биномиальное
(2) показательное
(3) гипергеометрическое
(4) вырожденное
(5) коши
(6) парето
Пусть math и math — произвольные случайные величины. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены math монет. При каждом math рассматривается событие math — на math-й монете выпал герб. Какие из следующих событий состоят в том, что выпали все решки?
(1) math
(2) math
(3) math
(4) math
Симметричную игральную кость подбрасывают трижды. Найдите математическое ожидание суммы выпавших очков.
(1) 0,5
(2) 9
(3) 10,5
(4) 12
(5) 18
Точка с координатами math и math наудачу выбрана в круге math. Найдите коэффициент корреляции координат точки и выберите верные утверждения.
(1) math и math независимы
(2) math и math зависимы
(3) math
(4) math
Пусть math — последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами math. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1/4
(3) 1/2
(4) 3/4
(5) предела не существует или указанных условий недостаточно
Имеется последовательность независимых и одинаково распределенных случайных величин. Укажите, при каких распределениях членов последовательности эта последовательность удовлетворяет центральной предельной теореме.
(1) биномиальное распределение с параметрами 4 и 1/3
(2) распределение Коши с параметрами 1 и 2
(3) распределение с плотностью math при math
(4) распределение с плотностью math при math
Укажите верные высказывания.
(1) если характеристические функции двух случайных величин совпадают, то все моменты (существующие) этих случайных величин совпадают
(2) если характеристическая функция равна math, то распределение вырождено в единице
(3) характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций
(4) если характеристическая функция тождественно равна единице, то распределение вырождено в единице
Из букв слова МОЛОКО, составленного с помощью разрезной азбуки, извлекают наудачу и выкладывают в порядке извлечения три буквы. Какова вероятность того, что при этом получится слово МОЛ?
(1) 1/20
(2) 1/40
(3) 1/120
(4) 1/60
Чему равна вероятность math для произвольных событий math и math?
(1) math
(2) math
(3) math
(4) math
Пусть события A, B, C попарно независимы. Выберите верные утверждения.
(1) события A и B независимы
(2) события A ∪ B и C независимы
(3) P(A ∩ B ∩ C) = P(A)P(B)P(C)
(4) события A, B, C попарно независимы
Прибор состоит из 100 независимо работающих элементов. Вероятность отказа любого из них при включении равна 0,01. По теореме Пуассона найдите приближенно вероятность того, что не откажет ни один элемент.
(1) 0,002
(2) 0,184
(3) 0,271
(4) 0,368
Какие из следующих функций являются плотностями распределений?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, для которых вероятность math является наибольшей среди перечисленных.
(1) math
(2) math
(3) math
(4) math
Пусть math и math имеют плотность совместного распределения math Укажите, чему равна вероятность события math.
(1) 0
(2) 0,25
(3) 0,5
(4) 1
Пусть math. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Пусть math. Выберите верное высказывание.
(1) math
(2) math
(3) math
(4) math
Случайные величины math независимы. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Подбрасывают две правильные монеты. После math подбрасываний двух монет обозначим через math количество подбрасываний, при которых выпал один герб и одна решка. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 1/2
(2) 0
(3) 1/6
(4) 1/4
(5) предела не существует
В точке math, положение которой на телефонной линии math длиной 100 км равновозможно, произошел разрыв линии. Какова вероятность того, что точка math удалена от точки math более, чем на 75 км?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Фирма A в течение года разоряется с вероятностью 0,3, фирма Б — с вероятностью 0,4, а обе фирмы — с вероятностью 0,25. Какова вероятность того, что в течение года разорится хотя бы одна фирма?
(1) 0,12
(2) 0,45
(3) 0,5
(4) 0,7
В первой урне 40% шаров белые, во второй — 50%. Из наудачу выбранной урны достают шар. Определите вероятность того, что шар окажется белым.
(1) 0, 45
(2) 0, 5
(3) 0, 9
(4) 0, 95
Проводится math испытаний схемы Бернулли с вероятностью успеха math. Укажите, при каких значениях math и math можно использовать теорему Пуассона для приближенного вычисления вероятностей, если погрешность приближения не должна превышать 0,05.
(1) math
(2) math
(3) math
(4) math
Пусть распределение случайной величины math задано плотностью распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Укажите распределение суммы двух независимых случайных величин math.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите верное отношение.
(1) math
(2) math
(3) math
(4) math
(5) math
(6) math
Пусть math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Пусть math — последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами math. Укажите, чему равен предел при math последовательности math в смысле сходимости почти наверное.
(1) 0
(2) 9/16
(3) 1/4
(4) 3/4
(5) 3/16
Две точки наудачу брошены на отрезок. Какова вероятность того, что расстояние между ними окажется не больше половины длины отрезка?
(1) 0, 25
(2) 1/3
(3) 0, 75
(4) 0, 5
Пусть math обозначает меру Лебега борелевского множества math. Укажите значение math.
(1) 0
(2) 1
(3) 2
(4) 3
В первой урне 20% шаров белые, во второй — 60%. Из наудачу выбранной урны наугад достали шар, оказавшийся белым. Определите вероятность того, что шар был вынут из второй урны.
(1) 0, 4
(2) 0, 5
(3) 0, 6
(4) 0, 75
Пусть распределение случайной величины math задано функцией распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Даны пять независимых в совокупности случайных величин math с одним и тем же распределением Бернулли с параметром 1/2. Найдите math.
(1) 5/16
(2) 0
(3) 1/8
(4) 1/32
Укажите, в какой последовательности распределений математические ожидания упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,3,1,4
(4) 4,3,1,2
(5) 3,2,1,4
Выберите последовательности случайных величин, удовлетворяющие закону больших чисел.
(1) случайные величины попарно некоррелированы и имеют одно и то же распределение Пуассона
(2) случайные величины независимы и имеют разные нормальные распределения, math
(3) случайные величины независимы (в совокупности), одинаково распределены и имеют конечный первый момент
(4) случайные величины независимы, math
Точка с координатами math и math наудачу бросается в квадрат math. Выберите верные высказывания.
(1) каждый элементарный исход имеет нулевую вероятность
(2) math
(3) math
(4) math
Даны события math такие, что math. Укажите значение math.
(1) 7/8
(2) 3/4
(3) 3/2
(4) 1
Пусть math) — произвольная функция распределения. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) плотность распределения суммы независимых случайных величин с абсолютно непрерывными распределениями равна произведению их плотностей
(2) сумма двух независимых случайных величин с дискретными распределениями имеет абсолютно непрерывное распределение
(3) сумма независимых случайных величин с одним и тем же показательным распределением имеет гамма-распределение
(4) сумма случайных величин с нормальными распределениями может иметь вырожденное распределение
Укажите, в какой последовательности распределений дисперсии упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,1,3,4
(4) 4,3,1,2
(5) 3,1,2,4
Считая, что math п. н. и указанные математические ожидания существуют, выберите верные неравенства.
(1) math
(2) math
(3) math
(4) math
Города А и Б соединены пятью дорогами. Сколькими способами можно добраться из города А в город Б и затем вернуться обратно?
(1) 32
(2) 10
(3) 20
(4) 25
Выберите распределения, у которых существует математическое ожидание.
(1) распределение, плотность которого равна нулю вне некоторого отрезка [a, b]
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии и связаны равенством math. Укажите значение их коэффициента корреляции.
(1) 0
(2) -1
(3) 1
(4) 2
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите функции, которые не могут быть характеристическими функциями никакой случайной величины.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите, какими могут быть вероятности элементарных исходов.
(1) 0, 1/3, 1/3
(2) 1/2, 1/6, 1/3
(3) 1/3, 2/3, 0
(4) 1, 1, -1
Пусть math — множество натуральных чисел. Какие из следующих множеств образуют алгебры подмножеств math?
(1) math
(2) math
(3) math
Пусть P(A) = 0, 3, P(B) = 0, 5, P(A ∩ B) = 0, 2. Найдите P(A|B).
(1) 0,15
(2) 0,2
(3) 0,4
(4) 0,6
Правильную монету подбросили 14 раз, и выпали только гербы. С какой вероятностью при 15-м броске выпадет решка?
(1) 1/2
(2) 1/215
(3) 15/215
(4) 15!/215
Пусть math — множество борелевских подмножеств отрезка math. Какие из следующих функций являются случайными величинами?
(1) math
(2) math
(3) math
(4) math
На отрезок [0, 1] наудачу и независимо друг от друга бросают пять точек. Какое распределение имеет число точек, попавших на левую половину отрезка?
(1) нормальное с параметрами 0,5 и 5
(2) равномерное на отрезке от 0 до 5
(3) биномиальное с параметрами 5 и 0,5
(4) геометрическое с параметром 5
Пусть случайный вектор math имеет абсолютно непрерывное распределение с плотностью math. Выберите верные высказывания.
(1) функция совместного распределения math равна интегралу math
(2) math
(3) функция совместного распределения всюду непрерывна
(4) math
Пусть math. Укажите значение вероятности math.
(1) 1/32
(2) 1/8
(3) 1/6
(4) 1/4
Сколькими способами можно составить список дежурных на пять дней следующей недели, если каждый день должен дежурить один человек, в классе всего 20 школьников, и ни один человек не должен дежурить более одного раза в неделю?
(1) math
(2) math
(3) math
(4) math
(5) 5
Выберите распределения, у которых существует дисперсия.
(1) распределение, плотность которого равна нулю вне некоторого отрезка [a, b]
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если math, то случайные величины math независимы
(2) math
(3) если math п. н., то math
(4) если math, то случайные величины math и math независимы
Дана последовательность случайных величин math со следующими распределениями: для любого math math Найдите предел последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) +∞
(4) 2
(5) math
Дана последовательность случайных величин math со следующими распределениями: math. Если последовательность math слабо сходится к некоторому распределению, найдите это распределение.
(1) math
(2) math
(3) math
(4) последовательность не сходится по распределению
Укажите, чему равна характеристическая функция случайной величины math.
(1) math
(2) math
(3) math
(4) math
Из урны, содержащей 3 белых и 2 черных шара, берут 2 шара наугад. Порядок появления шаров учитывается. Каково общее число равновозможных элементарных исходов?
(1) 3
(2) 5
(3) 4
(4) 6
Пусть math, а множество math содержит все конечные или счетные множества вещественных чисел (в том числе пустое) и их дополнения до math. Укажите верные высказывания.
(1) math
(2) math является σ-алгеброй
(3) math является алгеброй
(4) math
Пусть события A и B независимы, P(A) = 0, 4, P(B) = 0, 7. Выберите верное высказывание.
(1) P(A ∩ B) < P(A|B) < P(A ∪ B) < P(A)
(2) P(A|B) < P(A ∩ B) < P(A) < P(A ∪ B)
(3) P(A ∩ B) < P(A|B) < P(A) < P(A ∪ B)
(4) P(A) < P(A ∩ B) < P(A|B) < P(A ∪ B)
Дважды бросают симметричную игральную кость. Выберите верные высказывания.
(1) три очка в сумме выпадут с вероятностью 1/36
(2) выпадут две единицы с вероятностью 1/36
(3) выпадет ровно одна тройка с вероятностью 5/36
(4) выпадет ровно одна единица с вероятностью 5/18
Выберите верные утверждения.
(1) плотность абсолютно непрерывного распределения не обязательно непрерывна
(2) math
(3) если math, то распределения случайных величин math и math совпадают
(4) множество возможных значений случайной величины с дискретным распределением конечно
Случайная величина math имеет распределение Пуассона с параметром 1. Вычислите следующие вероятности и укажите верные равенства.
(1) math
(2) math
(3) math
(4) math
Случайная величина math имеет абсолютно непрерывное распределение с плотностью math. Пусть math. Какова плотность распределения случайной величины math?
(1) math
(2) math
(3) math
(4) math
На плоскости есть 6 точек. Каждые две из них можно соединить отрезком. Сколько таких отрезков можно образовать?
(1) math
(2) math
(3) math
(4) math
(5) math
Выберите верные утверждения.
(1) если математические ожидания и дисперсии у двух случайных величин совпадают, то эти случайные величины одинаково распределены
(2) math
(3) math
(4) дисперсия постоянной равна нулю
Случайные величины math и math независимы и имеют одно и то же распределение Бернулли с параметром 1/2. Найдите коэффициент корреляции случайных величин math.
(1) math
(2) 0
(3) math
(4) math
(5) math
Дана последовательность случайных величин math. Выберите достаточные условия для сходимости math.
(1) math
(2) math
(3) math
(4) math
Дана последовательность независимых и одинаково распределенных случайных величин с нормальным распределением с параметрами math. Пусть math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите распределение, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
На полке 6 книг по математике и 2 по физике. Какова вероятность того, что выбранная наугад книга окажется книгой по физике?
(1) 1/4
(2) 1/3
(3) 1/2
(4) 1/6
Пусть math содержащая множества math и math. Укажите множества, принадлежащие math.
(1) math
(2) math
(3) math
(4) math
Из урны, содержащей 2 белых и 3 черных шара, вынимают шары по одному до тех пор, пока не появится белый шар. Какова вероятность того, что из урны будет вынуто 4 шара?
(1) 0,4
(2) 0,3
(3) 0,2
(4) 0,1
Какая из формул вычисляет вероятность при семи подбрасываниях симметричной игральной кости ни разу не выбросить шесть очков?
(1) 7 · (5/6)7
(2) 1 - (1/6)7
(3) (5/6)7
(4) 1/7
Пусть задано вероятностное пространство — отрезок [0, 1] с сигмаалгеброй борелевских подмножеств и мерой Лебега в качестве вероятности. Укажите тип распределения случайной величины math, заданной равенством: math
(1) дискретное распределение
(2) абсолютно непрерывное распределение
(3) сингулярное распределение
(4) смешанное распределение
Случайная величина math имеет показательное распределение с параметром 2. Вычислите следующие вероятности и укажите верное неравенство.
(1) math
(2) math
(3) math
(4) math
Бросают две симметричные игральные кости. Случайная величина math равна сумме выпавших очков, случайная величина math равна числу выпавших двоек. Укажите вероятность события math.
(1) 1/12
(2) 1/18
(3) 1/36
(4) 5/36
(5) 5/162
Пусть math,math. Укажите значение плотности распределения случайной величины math в точке math.
(1) 1
(2) 1/2
(3) -1
(4) 0
Пусть math и math — произвольные события. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Найдите math, если случайная величина math имеет распределение с плотностью math
(1) не существует
(2) 1
(3) 3/2
(4) 2
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-505
000, 20, 3
-10, 10, 20, 2
Найдите ковариацию случайных величин math и math.
(1) 0
(2) -1
(3) 1
(4) 1/2
(5) 2
Пусть случайная величина math имеет распределение Пуассона с параметром math. Вероятность math можно оценить сверху по обобщенному неравенству Чебышева с помощью функции math. Укажите значение этой оценки.
(1) 1/210
(2) e2/210
(3) 1/e2
(4) 1
Дана последовательность независимых и одинаково распределенных случайных величин с распределением Бернулли с параметром math. Пусть math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите математическое ожидание и дисперсию распределения, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Из колоды в 36 карт наудачу выбирают шесть карт. Какова вероятность того, что среди них окажется хотя бы один король?
(1) math
(2) math
(3) math
(4) math
Пусть math. Выберите функции, которые являются вероятностными мерами.
(1) math
(2) math
(3) math
(4) math
Два раза подбрасывают монету. Укажите верные высказывания.
(1) события "при первом броске выпал герб" и "при первом броске выпала решка" несовместны
(2) события "при первом броске выпал герб" и "при втором броске выпал герб" независимы
(3) события "при первом броске выпал герб" и "при втором броске выпала решка" независимы,
(4) события "при первом броске выпал герб" и "при втором броске выпала решка" несовместны.
Стрелок попадает в цель при любом выстреле с вероятностью 0,1. Результаты выстрелов независимы. Какова вероятность того, что первое попадание случится при третьем выстреле?
(1) 0,81
(2) 0,1
(3) 0,243
(4) 0,081
Пусть случайная величина math принимает только значения math с одинаковой вероятностью math. Найдите math.
(1) 0
(2) 1/6
(3) 0,5
(4) 1
Случайная величина math имеет нормальное распределение с плотностью распределения math. Пусть math — функция распределения стандартного нормального распределения. Чему равно значение вероятности math?
(1) math
(2) math
(3) math
(4) math
Пусть случайный вектор math имеет абсолютно непрерывное распределение с постоянной плотностью во всех точках ромба math. Вне ромба плотность нулевая. Каково значение плотности внутри ромба?
(1) 1
(2) 1/2
(3) 1/2π
(4) 1/π
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Брошены пять монет. Рассматриваются события math — выпали пять гербов, math — выпали пять решек, math — выпала ровно одна решка. Выберите верное высказывание.
(1) math
(2) math
(3) math
Найдите math, если случайная величина math принимает только значения 1, 2 и 4 с равными вероятностями.
(1) 3/7
(2) 7/12
(3) 1/2
(4) 21
Случайные величины math имеют конечные дисперсии. Укажите верные утверждения.
(1) если величины math
(2) если величины math
(3) math
(4) math
Пусть math. Укажите, каким числом оценивется по неравенству Чебышева вероятность math.
(1) 1/3
(2) 1/9
(3) 1/27
(4) 1
Правильная монета подбрасывается 6400 раз. Используя ЦПТ, найдите приближенно вероятность того, что число гербов будет отличаться от 3200 не менее, чем на 120.
(1) math
(2) math
(3) math
(4) math
(5) math
Если математическое ожидание и дисперсия случайной величины math равны единице, как выглядит разложение ее характеристической функции в ряд Тейлора в окрестности нуля?
(1) math
(2) math
(3) math
(4) math
Из коробки, в которой лежали 5 красных и 2 синих карандаша, потерялись 4 карандаша. Какова вероятность того, что потерялись только красные карандаши, если любой карандаш имел равные шансы быть потерянным?
(1) 4/5
(2) 1/7
(3) 5/7
(4) 2/7
Пусть math обозначает меру Лебега борелевского множества math. Укажите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть события A и B независимы, P(A) = 0,5 и P(B) = 0,5. Укажите верные высказывания.
(1) события A и B совместны
(2) P(A ∪ B) = 3/4
(3) P(A ∩ B) = 1/4
(4) одно из этих событий влечет другое
Симметричную игральную кость подбрасывают 5 раз. Какова вероятность при этом трижды получить четное число очков и по разу — тройку и пятерку?
(1) 5/72
(2) 1/65
(3) 8/65
(4) 3/65
Пусть распределение случайной величины math задано таблицей распределения:
ai-3-213
P(ξ = ai)0, 20, 3p0, 1
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите абсолютно непрерывные распределения.
(1) биномиальное
(2) показательное
(3) гипергеометрическое
(4) вырожденное
(5) Коши
(6) Парето
Укажите высказывания, которые справедливы для любых случайных величин math и math с дискретными распределениями.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите, какая из следующих случайных величин имеет распределение math.
(1) math
(2) math
(3) math
(4) math
Каждая из math деталей может быть годной или дефектной. Событие math состоит в том, что math-я деталь дефектна. Какие из следующих событий означают, что хотя бы одна из деталей годная?
(1) math
(2) math
(3) math
(4) math
Симметричную игральную кость подбрасывают дважды. Найдите математическое ожидание суммы выпавших очков.
(1) 0,5
(2) 6
(3) 6,5
(4) 7
(5) 12
Случайная величина math принимает значения -1, 0 и 1 с равными вероятностями, math. Найдите коэффициент корреляции случайных величин math и math и выберите верные утверждения.
(1) math и math независимы
(2) math и math зависимы
(3) math
(4) math
Пусть math — последовательность независимых случайных величин с одним и тем же стандартным распределением Коши. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) -1
(4) предела не существует или указанных условий недостаточно
Имеется последовательность независимых и одинаково распределенных случайных величин. Укажите, при каких распределениях членов последовательности эта последовательность удовлетворяет центральной предельной теореме.
(1) распределение с плотностью math при math
(2) равномерное распределение на отрезке [0, 1]
(3) распределение с плотностью math при math
Укажите характеристическую функцию среднего арифметического math независимых в совокупности и одинаково распределјнных случайных величин с характеристической функцией math.
(1) math
(2) math
(3) math
(4) math
Из букв слова МОЛОКО, составленного с помощью разрезной азбуки, извлекают наудачу и выкладывают в порядке извлечения три буквы. Какова вероятность того, что при этом получится слово ОКО?
(1) 1/20
(2) 1/40
(3) 1/120
(4) 1/60
Выберите свойства, верные для произвольных событий math и math.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) если события попарно независимы, то они независимы в совокупности
(2) если события A, B, C независимы в совокупности, то события A ∪ B и C независимы
(3) если P(A ∩ B ∩ C) = P(A)P(B)P(C), то события A, B, C независимы в совокупности
(4) если события независимы в совокупности, то они попарно независимы
Каждая из 1000 деталей с вероятностью 0,001 может оказаться бракованной. По теореме Пуассона найдите приближенно вероятность того, что ровно две детали будут бракованными.
(1) 0,002
(2) 0,184
(3) 0,271
(4) 0,368
Какие из следующих функций являются плотностями распределений?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, для которых вероятность math является наибольшей среди перечисленных.
(1) math
(2) math
(3) math
(4) math
Пусть math и math имеют плотность совместного распределения math Укажите, чему равна вероятность события math.
(1) 0
(2) 0,25
(3) 0,5
(4) 1
Пусть math. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Пусть math. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Случайные величины math независимы. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Подбрасывают правильную игральную кость. Величина math равна сумме выпавших очков. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 1, 5
(2) 0
(3) 3, 5
(4) 3
(5) предела не существует
В точке math, положение которой на телефонной линии math длиной 100 км равновозможно, произошел разрыв линии. Какова вероятность того, что точка math удалена от точки math более, чем на 25 км?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Из колоды в 36 карт наугад берут одну. Какова вероятность получить любого короля или любую карту пиковой масти?
(1) 1/3
(2) 1/36
(3) 1/4
(4) 13/36
В фирме половина работающих — мужчины. Вероятность опоздать на работу в произвольно взятый день для мужчины равна 0,1, для женщины — 0,3. Определите вероятность того, что наугад выбранный из списка сотрудник завтра опоздает на работу.
(1) 0, 03
(2) 0, 1
(3) 0, 2
(4) 0, 5
Проводится math испытаний схемы Бернулли с вероятностью успеха math. Укажите, при каких значениях math и math можно использовать теорему Пуассона для приближенного вычисления вероятностей, если погрешность приближения не должна превышать 0,001.
(1) math
(2) math
(3) math
(4) math
Пусть распределение случайной величины math задано плотностью распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть случайная величина math имеет нормальное распределение с параметрами math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Укажите распределение суммы двух независимых случайных величин math.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите верное отношение.
(1) math
(2) math
(3) math
(4) math
(5) math
(6) math
Пусть math. Выберите верное утверждение.
(1) math
(2) math
(3) math
(4) math
(5) math
Пусть math — последовательность независимых случайных величин с одним и тем же распределением Пуассона с параметром 2. Укажите, чему равен предел при math последовательности math в смысле сходимости почти наверное.
(1) 0
(2) 1
(3) 2
(4) 4
(5) 6
На отрезке [0, 1] наудачу выбираются две точки. Какова вероятность того, что расстояние между ними окажется больше, чем 0, 1?
(1) 0, 01
(2) 0, 81
(3) 0, 1
(4) 0, 09
Укажите свойства, которыми обладает любая вероятностная мера.
(1) math
(2) math
(3) math
(4) math
В первой урне 60% шаров белые, во второй — 20%. Из наудачу выбранной урны наугад достали шар, оказавшийся белым. Определите вероятность того, что шар был вынут из второй урны.
(1) 0, 2
(2) 0, 25
(3) 0, 4
(4) 0, 5
Пусть распределение случайной величины math задано функцией распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Даны три независимые в совокупности случайные величины math с одним и тем же распределением Пуассона с параметром 2. Найдите math.
(1) math
(2) math
(3) math
(4) math
Укажите, в какой последовательности распределений математические ожидания упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,3,1,4
(4) 4,3,1,2
(5) 3,2,1,4
Выберите последовательности случайных величин, удовлетворяющие закону больших чисел.
(1) случайные величины попарно некоррелированы и имеют одно и то же распределение с конечным вторым моментом
(2) случайные величины независимы и равномерно распределены на отрезке [0, 1]
(3) случайные величины независимы, math
Даны события math такие, что math. Укажите значение math.
(1) 7/8
(2) 3/4
(3) 3/2
(4) 1
Пусть распределение случайной величины math абсолютно непрерывно, math — функция распределения случайной величины math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) для независимых случайных величин с абсолютно непрерывными распределениями плотность распределения их суммы равна math
(2) для независимых случайных величин с абсолютно непрерывными распределениями плотность распределения их суммы равна math
(3) сумма независимых случайных величин с одним и тем же распределением Бернулли имеет биномиальное распределение
(4) разность независимых случайных величин с нормальными распределениями может иметь вырожденное распределение
Укажите, в какой последовательности распределений дисперсии упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,1,3,4
(4) 4,3,1,2
(5) 3,1,2,4
Считая, что указанные математические ожидания существуют, выберите верные неравенства.
(1) math
(2) math
(3) math
(4) math
Сколькими способами можно выбрать одну гласную и одну согласную буквы из слова "скрипач"?
(1) 32
(2) 10
(3) 20
(4) 25
Выберите распределения, у которых существует математическое ожидание.
(1) распределение с функцией распределения math
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии и связаны равенством math. Укажите значение их коэффициента корреляции.
(1) 0
(2) -1
(3) 1
(4) 2
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите функции, которые не могут быть характеристическими функциями никакой случайной величины.
(1) math
(2) math
(3) math
(4) math
Пусть пространство math совпадает с множеством всех натуральных чисел. Укажите, какими могут быть вероятности элементарных исходов.
(1) все равны math
(2) все равны нулю
(3) 1/2, 1/3, 1/4, 1/5, . . .
(4) 1/2, 1/4, 1/8, 1/16, . . .
Пусть math — множество целых чисел. Какие из следующих множеств образуют алгебры подмножеств math?
(1) math
(2) math
(3) math
(4) math
Один раз бросают симметричную игральную кость. Событие A — выпало 3 очка, событие B — выпало нечетное число очков. Найдите P(A|B).
(1) 1/6
(2) 1/3
(3) 1/2
(4) 1
Симметричную игральную кость бросали 29 раз, и ни разу не выпало шесть очков. С какой вероятностью при 30-м броске выпадет шесть очков?
(1) (5/6)29 · (1/6)
(2) 1/6
(3) 5 · (5/6)30
(4) 1
Пусть math. Какие из следующих функций являются случайными величинами?
(1) math
(2) math
(3) math
(4) math
Симметричную игральную кость бросают до тех пор, пока впервые не выпадет шесть очков. Какое распределение имеет число выполненных бросаний кости?
(1) распределение Пуассона с параметром 6
(2) равномерное на отрезке от 0 до 6
(3) биномиальное с параметрами 6 и 1/6
(4) геометрическое с параметром 1/6
Пусть случайный вектор math имеет абсолютно непрерывное распределение с плотностью math. Выберите верные высказывания.
(1) функция совместного распределения math равна интегралу math
(2) math
(3) плотность совместного распределения всюду непрерывна
(4) math
Пусть math. Укажите значение вероятности math.
(1) 8/27
(2) 1/27
(3) 2/9
(4) 4/9
Сколькими способами можно выбрать спорторга, культорга и председателя редколлегии, если всего в классе 20 школьников?
(1) math
(2) math
(3) math
(4) math
(5) 3
Выберите распределения, у которых существует дисперсия.
(1) распределение с функцией распределения math
(2) распределение с функцией распределения math
(3) распределение с функцией распределения math
(4) распределение math
Случайные величины math и math имеют конечные и ненулевые дисперсии. Укажите верные утверждения.
(1) если math, то случайные величины math зависимы
(2) math
(3) если math п. н. при некоторых math и math
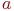(4) если math, то случайные величины math и math независимы
Дана последовательность случайных величин math со следующими распределениями: для любого math math Найдите предел последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1
(3) +∞
(4) 2
(5) math
Дана последовательность случайных величин math со следующими распределениями: math Если последовательность math слабо сходится к некоторому распределению, найдите это распределение.
(1) math
(2) math
(3) math
(4) последовательность не сходится по распределению
Укажите, чему равна характеристическая функция случайной величины math.
(1) math
(2) math
(3) math
(4) math
Из урны, содержащей 3 белых и 2 черных шара, дважды берут шар наугад, возвращая его обратно. Каково общее число равновозможных элементарных исходов?
(1) 3
(2) 10
(3) 20
(4) 25
Пусть math — произвольное непустое конечное множество, math — некоторое множество подмножеств Ω. Укажите верные высказывания.
(1) если math — алгебра, то math — σ-алгебра
(2) если math — σ-алгебра, то math — тривиальная σ-алгебра
(3) множество math конечно
(4) множество math не может являться σ-алгеброй
Пусть события A и B независимы, P(A) = 0, 8, P(B) = 0, 2. Выберите верное высказывание.
(1) P(A ∩ B) < P(A) < P(A|B) < P(A ∪ B)
(2) P(A|B) < P(A ∩ B) < P(A) < P(A ∪ B)
(3) P(A ∩ B) < P(A|B) < P(A) < P(A ∪ B)
(4) P(A) < P(A ∩ B) < P(A|B) < P(A ∪ B)
Пять раз подбрасывают правильную монету. Выберите верные высказывания.
(1) пять раз выпадет герб с вероятностью 1/5
(2) при третьем броске выпадет герб с вероятностью 1/8
(3) если при четырех бросках выпал орел, то при пятом броске вероятнее выпасть решке
(4) пять решек выпадут с вероятностью 1/32
Выберите верные утверждения.
(1) дискретное распределение имеет плотность распределения
(2) math
(3) если math, то распределения случайных величин math и math совпадают
(4) одинаково распределенные случайные величины совпадают
Случайная величина math имеет показательное распределение с параметром 2. Вычислите следующие вероятности и укажите верные равенства.
(1) math
(2) math
(3) math
(4) math
Случайная величина math имеет абсолютно непрерывное распределение с плотностью math. Пусть math. Какова плотность распределения случайной величины math?
(1) math
(2) math
(3) math
(4) math
В турнире принимают участие 6 шахматистов. Сколькими способами можно их разбить на две группы по три шахматиста?
(1) 6
(2) 8
(3) 20
(4) 64
(5) 120
Выберите верные утверждения.
(1) если math то math с вероятностью 1
(2) math
(3) math
(4) дисперсия суммы независимых случайных величин равна сумме дисперсий
Случайные величины math и math независимы и имеют одно и то же равномерное распределение на отрезке [0, 1]. Найдите коэффициент корреляции случайных величин math.
(1) math
(2) 0
(3) math
(4) math
(5) math
Дана последовательность случайных величин math. Выберите достаточные условия для сходимости math.
(1) math
(2) math
(3) math
(4) не требуется никаких дополнительных условий
Дана последовательность независимых и одинаково распределенных случайных величин с распределением Пуассона с параметром math, math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите распределение, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Три карточки с буквами К, Т, О выкладывают в ряд в произвольном порядке. Какова вероятность выложить слово КОТ?
(1) 1/3
(2) 1/2
(3) 1/6
(4) 1
Пусть math содержащая множества math и math. Укажите множества, принадлежащие math.
(1) math
(2) math
(3) math
(4) math
Из урны, содержащей 2 белых и 3 черных шара, вынимают шары по одному до тех пор, пока не появится белый шар. Какова вероятность того, что из урны будет вынуто только 2 шара?
(1) 0,4
(2) 0,3
(3) 0,2
(4) 0,1
Какая из формул вычисляет вероятность при шести подбрасываниях симметричной игральной кости ровно один раз выбросить шесть очков?
(1) (5/6)6
(2) (5/6)5
(3) 1 - (1/6)7
(4) 1
Пусть задано вероятностное пространство — отрезок [0, 1] с сигма алгеброй борелевских подмножеств и мерой Лебега в качестве вероятности. Укажите тип распределения случайной величины math, заданной равенством: math
(1) дискретное распределение
(2) абсолютно непрерывное распределение
(3) сингулярное распределение
(4) смешанное распределение
Случайная величина math имеет стандартное нормальное распределение. Укажите верное неравенство.
(1) math
(2) math
(3) math
(4) math
Бросают две симметричные игральные кости. Случайная величина math равна сумме выпавших очков, случайная величина math равна числу выпавших двоек. Укажите вероятность события math.
(1) 1/12
(2) 1/18
(3) 1/36
(4) 5/36
(5) 125/1296
Случайная величина math имеет распределение Парето с плотностью math при math. Укажите значение плотности распределения случайной величины math в точке math.
(1) 1/9
(2) 1/8
(3) -7/9
(4) 0
Выберите все верные высказывания.
(1) противоположные события несовместны
(2) несовместные события противоположны
(3) невозможное событие несовместно с любым другим
(4) невозможное событие совместно с самим собой
(5) пересечение любого числа попарно несовместных событий невозможно
Найдите math, если случайная величина math имеет распределение с плотностью math
(1) не существует
(2) 3/4
(3) 3/2
(4) 4/3
Случайные величины math и math имеют следующую таблицу совместного распределения:
ηξ-10010
000, 20, 3
-10, 10, 20, 2
Найдите ковариацию случайных величин math и math.
(1) 0
(2) -1
(3) 1
(4) 1/2
(5) 2
Пусть случайная величина math имеет распределение Пуассона с параметром math. Вероятность math можно оценить сверху по обобщенному неравенству Чебышева с помощью функции math. Укажите значение этой оценки.
(1) 1/310
(2) e3/310
(3) 1/e3
(4) e6/310
Дана последовательность независимых и одинаково распределенных случайных величин с распределением Пуассона с параметром math, math - сумма первых math случайных величин в этой последовательности. Последовательность math слабо сходится к некоторому распределению. Найдите это распределение.
(1) math
(2) math
(3) math
(4) math
(5) math
Укажите математическое ожидание и дисперсию распределения, которому отвечает характеристическая функция math.
(1) math
(2) math
(3) math
(4) math
(5) math
Из колоды в 36 карт наудачу выбирают шесть карт. Какова вероятность того, что среди них окажется ровно один король?
(1) math
(2) math
(3) math
(4) math
Пусть math Выберите функции, которые являются мерами.
(1) math
(2) math
(3) math
(4) math
Пусть события A и B независимы, P(A) = 0, 5, P(B) = 0, 5. Укажите верные высказывания.
(1) события A и B несовместны
(2) P(A ∪ B) = 1
(3) P(A ∩ B) = 0
(4) P(A|B) = 0, 5
Стрелок, попадающий в цель при любом выстреле с вероятностью 0,1, ведет стрельбу до первого попадания. Результаты выстрелов независимы. Какова вероятность того, что потребуется не менее трех патронов?
(1) 0,81
(2) 0,1
(3) 0,243
(4) 0,081
Пусть случайная величина math принимает только значения math с одинаковой вероятностью math. Найдите math.
(1) 0,2
(2) 0,4
(3) 0,6
(4) 0,8
Случайная величина math имеет нормальное распределение с параметрами math и math. Пусть math — функция распределения стандартного нормального распределения. Чему равно значение вероятности math?
(1) math
(2) math
(3) math
(4) math
Пусть случайный вектор math имеет абсолютно непрерывное распределение с плотностью math Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
Пусть math. Укажите распределение случайной величины math.
(1) math
(2) math
(3) math
(4) math
Брошены пять монет. Рассматриваются события math — выпали пять гербов, math — выпали пять решек, math — выпала ровно одна решка. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Найдите math, если случайная величина math принимает только значения -1, 0 и 1 с равными вероятностями.
(1) 0
(2) 5/6
(3) 1
(4) 7/6
Укажите верные утверждения.
(1) число гербов и число решек при 10 бросаниях правильной монеты некоррелированы
(2) число гербов и число решек при 10 бросаниях правильной монеты отрицательно коррелированы
(3) число гербов при первых 10 и число решек при следующих 10 бросаниях правильной монеты некоррелированы
(4) число гербов при первых 10 и число решек при следующих 10 бросаниях правильной монеты независимы
Пусть math. Укажите, каким числом оценивется по неравенству Чебышева вероятность math.
(1) 0, 2
(2) 0, 05
(3) 0, 04
(4) 0, 01
Правильная монета подбрасывается 6400 раз. Используя ЦПТ, найдите приближенно вероятность того, что число гербов будет отличаться от 3200 не менее, чем на 80.
(1) math
(2) math
(3) math
(4) math
(5) math
Если последовательность характеристических функций math сходится при всех math к характеристической функции math, что можно сказать про поведение случайных величин math?
(1) сходятся к math почти наверное
(2) сходятся к math по вероятности
(3) сходятся к math по распределению
(4) совпадают с math
Из коробки, в которой лежали 5 красных и 2 синих карандаша, потерялись 3 карандаша. Какова вероятность того, что потерялись только красные карандаши, если любой карандаш имел равные шансы быть потерянным?
(1) 4/5
(2) 1/7
(3) 5/7
(4) 2/7
Пусть math обозначает меру Лебега борелевского множества math. Укажите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть события A и B независимы, P(A) = 0, 5, P(B) = 0, 5. Укажите верные высказывания.
(1) P(A ∩ B) = 1/4
(2) эти события в объединении дают достоверное событие
(3) P(A|B) = 1/2
(4) P(B |A) = 1/2
Симметричную игральную кость подбрасывают 6 раз. Какова вероятность при этом выбросить каждую грань по разу?
(1) 1/66
(2) 1/65
(3) 56/66
(4) 6!/66
Пусть распределение случайной величины math задано таблицей распределения:
ai-2-101
P(ξ = ai)0, 10, 2p0, 1
Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Распределение случайной величины math ограничено, если найдется число math такое, что math. Выберите ограниченные распределения.
(1) биномиальное
(2) геометрическое
(3) равномерное на отрезке
(4) нормальное
(5) пуассона
(6) вырожденное>
Укажите верные высказывания.
(1) math
(2) попарная независимость влечет независимость в совокупности
(3) если случайная величина не зависит от самой себя, то она имеет вырожденное распределение
(4) если случайная величина имеет вырожденное распределение, то она не зависит от самой себя
Пусть math. Укажите, какая из следующих случайных величин имеет распределение Парето с плотностью math при math.
(1) math
(2) math
(3) math
(4) math
Каждая из math деталей может быть годной или дефектной. Событие math состоит в том, что math-я деталь дефектна. Какие из следующих событий означают, что все детали годные?
(1) math
(2) math
(3) math
(4) math
Сделано пять выстрелов по мишени. Вероятность попадания при каждом из первых трех выстрелов равна 0,5, при каждом из двух последних — 0,7. Найдите математическое ожидание числа попаданий.
(1) 0,6
(2) 2,5
(3) 2,9
(4) 3
(5) 0,58
Пусть math — последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами math. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 0
(2) 1/4
(3) 1/2
(4) 1
(5) предела не существует или указанных условий недостаточно
Имеется последовательность независимых и одинаково распределенных случайных величин. Укажите, при каких распределениях членов последовательности эта последовательность удовлетворяет центральной предельной теореме.
(1) распределение с плотностью math при math
(2) равномерное распределение на отрезке [-1, 1]
(3) распределение Бернулли с параметром 1/2
(4) распределение с плотностью math при math
На некотором вероятностном пространстве задана последовательность случайных величин math. Известно, что последовательность их характеристических функций сходится при всех math к характеристической функции math. Какой вывод можно сделать о поведении последовательности случайных величин math?
(1) math
(2) math
(3) math
(4) math
Выберите свойства, верные для любых несовместных событий math и math.
(1) math
(2) math
(3) math
Выберите верные утверждения.
(1) если P(A1 ∩ . . . ∩ An) = P(A1) · . . . ·P(An), то события A1, . . . ,An независимы в совокупности
(2) если события A, B, C независимы в совокупности, то и события A, B и C независимы в совокупности
(3) если P(A ∩ B ∩ C) ≠ P(A)P(B)P(C), то события A, B, C не являются независимыми в совокупности
(4) события Ω и ∅ независимы
Каждая из 1000 деталей с вероятностью 0,001 может оказаться бракованной. По теореме Пуассона найдите приближенно вероятность того, что ровно одна деталь будет бракованной.
(1) 0,002
(2) 0,184
(3) 0,271
(4) 0,368
Какие из следующих функций являются плотностями распределений?
(1) math
(2) math
(3) math
(4) math
Выберите распределения, для которых вероятность math является наибольшей среди перечисленных.
(1) math
(2) math
(3) math
(4) math
Пусть math и math имеют плотность совместного распределения math Укажите, чему равна вероятность события math.
(1) math
(2) math
(3) math
(4) math
Случайную величину, имеющую абсолютно непрерывное распределение, умножили на 2. Выберите верные высказывания.
(1) тогда ее плотность увеличится вдвое
(2) тогда график ее плотности сдвинется на 2 влево
(3) тогда график ее функции распределения растянется вдвое по оси абсцисс
(4) тогда график ее плотности сожмется вдвое по оси ординат и растянется вдвое по оси абсцисс
Пусть math. Выберите все верные высказывания.
(1) math
(2) math
(3) math
(4) math
Случайные величины math независимы. Выберите верные высказывания.
(1) math
(2) math
(3) math
(4) math
(5) math
Подбрасывают три правильные монеты. После math подбрасываний этих трех монет обозначим через math количество подбрасываний, при которых выпало не более одного герба. Укажите, чему равен предел при math последовательности math в смысле сходимости по вероятности.
(1) 1/2
(2) 0
(3) 1/6
(4) 1/4
(5) предела не существует
В точке math, положение которой на телефонной линии math длиной 100 км равновозможно, произошел разрыв линии. Какова вероятность того, что точка math удалена и от точки math, и от точки math более, чем на 40 км?
(1) 0, 25
(2) 0, 2
(3) 0, 75
(4) 0, 5
Из колоды в 36 карт наугад берут одну. Какова вероятность получить любого короля или любую карту пиковой масти?
(1) 1/3
(2) 1/36
(3) 1/4
(4) 13/36
Первый стрелок попадает в цель в 70% случаев, второй — в половине случаев. Выбранный случайным образом стрелок произвел выстрел. Определите вероятность попадания в цель.
(1) 0, 35
(2) 0, 5
(3) 0, 6
(4) 1, 2
Проводится math испытаний схемы Бернулли с вероятностью успеха math. Укажите, при каких значениях math и math можно использовать теорему Пуассона для приближенного вычисления вероятностей, если погрешность приближения не должна превышать 0,01.
(1) math
(2) math
(3) math
(4) math
Пусть распределение случайной величины math задано плотностью распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Пусть случайная величина math имеет нормальное распределение с параметрами math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Укажите распределение разности двух независимых случайных величин с одним и тем же нормальным распределением с параметрами math.
(1) math
(2) math
(3) math
(4) math
Пусть math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Пусть math — последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами math. Укажите, чему равен предел при math последовательности math в смысле сходимости почти наверное.
(1) 0
(2) 1
(3) 3
(4) 4
(5) 5
На отрезке [0, 1] наудачу выбираются две точки. Какова вероятность того, что расстояние между ними окажется больше, чем 0, 9?
(1) 0, 01
(2) 0, 81
(3) 0, 1
(4) 0, 09
Укажите свойства, которыми обладает любая вероятностная мера.
(1) math
(2) math
(3) math
(4) math
Первый стрелок попадает в цель всегда, второй — в половине случаев. Выбранный случайным образом стрелок произвел выстрел и попал в мишень. Какова вероятность, что стрелял второй стрелок?
(1) 0
(2) 1/2
(3) 1/3
(4) 2/3
Пусть распределение случайной величины math задано функцией распределения: math Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
(5) math
Даны шесть независимых в совокупности случайных величин math с одним и тем же распределением Бернулли с параметром 1/2. Найдите math.
(1) 5/16
(2) 0
(3) 1/64
(4) 3/32
Укажите, в какой последовательности распределений математические ожидания упорядочены по возрастанию: (1) U-5, 5; (2) П4; (3) N-5, 16; (4) G1/2.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,3,1,4
(4) 4,3,1,2
(5) 3,2,1,4
Выберите последовательности случайных величин, удовлетворяющие закону больших чисел.
(1) случайные величины совпадают, т. е. math, и имеют вырожденное распределение
(2) случайные величины независимы и их дисперсии ограничены одной и той же постоянной
(3) случайные величины независимы, одинаково распределены и имеют конечный четвертый момент
(4) ковариации любых двух случайных величин math отрицательны, а все дисперсии ограничены одной и той же постоянной
Даны события math такие, что math, math, math. Укажите значение math.
(1) 7/8
(2) 3/4
(3) 3/2
(4) 1
Пусть распределение случайной величины math абсолютно непрерывно, math — функция распределения, а math — плотность распределения случайной величины math. Выберите верные утверждения.
(1) math
(2) math
(3) math
(4) math
Выберите верные утверждения.
(1) для независимых случайных величин с абсолютно непрерывными распределениями плотность распределения их суммы равна math
(2) для независимых случайных величин с абсолютно непрерывными распределениями плотность распределения их суммы равна math
(3) сумма независимых случайных величин с одним и тем же распределением Бернулли имеет распределение Бернулли
(4) разность независимых случайных величин с нормальными распределениями имеет нормальное распределение
Укажите, в какой последовательности распределений дисперсии упрядочены по возрастанию. Здесь math.
(1) 1,2,4,3
(2) 3,1,4,2
(3) 2,1,3,4
(4) 4,3,1,2
(5) 3,1,2,4
Считая, что указанные математические ожидания существуют, выберите верные неравенства.
(1) math
(2) math
(3) math
(4) math