Главная /
Математика /
Введение в линейную алгебру
Введение в линейную алгебру - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: В курсе последовательно излагаются методы решения линейных уравнений, даются основы для использования матриц, векторов и линейных пространств.
Все ответы: В курсе последовательно излагаются методы решения линейных уравнений, даются основы для использования матриц, векторов и линейных пространств.
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если
, то
A+B равно
(1)
(2)
(3) нельзя
(4) можно так сделать, но предварительно надо вычислить каждый из определителей по формуле
Дана система
.
Детерминантом этой системы будет число, равное
(1) 5
(2) 6
(3) -5
(4) -1
К диагональному виду можно привести
(1) любую линейную систему уравнений
(2) совместную линейную систему уравнений
(3) систему уравнений, в которой количество независимых уравнений равно количеству неизвестных в системе
Вектором называется
(1) физическая величина, характеризующаяся направлением и своей величиной
(2) отрезок определенного направления
(3) отрезок определенной длины
Компланарность трех векторов проверяют при помощи
(1) смешанного произведения
(2) векторного произведения
(3) скалярного произведения
Компланарность трех векторов проверяют при помощи
(1) смешанного произведения
(2) векторного произведения
(3) скалярного произведения
Определите, является ли числовым полем следующее множество:
1 2 3 5 6
(1) да
(2) нет
Подпространством линейного пространства
R является ...
(1) совокупность его элементов
R1, которая сама является линейным пространством
(2) совокупность его элементов
R1, которая сама является линейным пространством относительно введенных в R операций сложения и умножения на число
(3) множества векторов на всех плоскостях и всех прямых, проходящих через начало координат
(4) подпространства
R1, размерность которого должна быть меньше или равна размерности пространства R Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) 2
(3) -3
(4) -13
(5) ни один из данных ответов.
Элементы
аij, из которых составлена матрица называются
(1) коэффициентами матрицы
(2) элементами данной матрицы
(3) элементами таблицы
Если строки в матрице поменять со столбцами, то эта операция называется
(1) обращением матрицы
(2) транспонированием матрицы
(3) переворотом матрицы
Система называется неопределенной, если
(1) имеет единственное решение
(2) имеет любое количество решений
(3) имеет по крайней мере два различных решения
Система называется неоднородной, если
(1) среди свободных членов хотя бы один не равен нулю
(2) имеет любое количество решений
(3) все свободные члены равны нулю
Векторы, расположенные на одной прямой или на параллельных прямых называются
(1) коллинеарными
(2) компланарными
(3) сонаправленными
Произведением ненулевого вектора ![math]() на действительное число
на действительное число
 на действительное число
на действительное число x ≠ 0 называется
(1) число, равное произведению числа ![math]()
х на модуль вектора 
(2) вектор, длина которого равна произведению длины вектора ![math]() на модуль числа
на модуль числа ![math]()
 на модуль числа
на модуль числа х, а направление совпадает, если x>0, или не совпадает, если x<0, с направлением исходного вектора 
(3) вектор, длина которого равна произведению длины вектора ![math]() на модуль числа
на модуль числа
 на модуль числа
на модуль числа х Произведением ненулевого вектора ![math]() на действительное число
на действительное число
 на действительное число
на действительное число x ≠ 0 называется
(1) число, равное произведению числа ![math]()
х на модуль вектора 
(2) вектор, длина которого равна произведению длины вектора ![math]() на модуль числа
на модуль числа ![math]()
 на модуль числа
на модуль числа х, а направление совпадает, если x>0, или не совпадает, если x<0, с направлением исходного вектора 
(3) вектор, длина которого равна произведению длины вектора ![math]() на модуль числа
на модуль числа
 на модуль числа
на модуль числа х Определите, является ли данное множество линейным пространством:
0 1 2 3 4 ... 100 101 ... М М+1 ...
(1) да
(2) нет
Если в пространстве можно задать длину, то такое пространство называют...
(1) аффинным
(2) метрическим
(3) независимым
(4) евклидовым
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Матрицей называется
(1) любая прямоугольная таблица, составленная из неизвестных систем
(2) любая прямоугольная таблица, составленная из коэффициентов систем
(3) любая таблица, составленная из
аij Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Для того, чтобы система имела единственное решение по формулам Крамера необходимо, чтобы
(1)
Δ ≠ 0
(2)
Δ = 0
(3)
Δ > 0 Расстояние между точками
A(1;1) и B(0;3) равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов
a(3;-1;2) и b(-1;4;5). Выбрать правильный ответ
(1) 9
(2) 11
(3) 3
(4) 2
(5) 8
Найти скалярное произведение векторов
a(3;-1;2) и b(-1;4;5). Выбрать правильный ответ
(1) 9
(2) 11
(3) 3
(4) нет правильного ответа
Определите какие из приведенных множеств являются отображаемыми по отношению к исходному (данному):
1 2 3 5 8 9
(1) 99 98 95 93 92 91
(2) -5 -1 -9 -2 -3 -8
(3) 1 2 2 3 5 8 9
Если некоторая величина может быть охарактеризована только своим значением, то такую величину называют...
(1) базисной
(2) векторной
(3) скалярной
(4) положительной или отрицательной
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Алгебраическим дополнением
Аij называется
(1) минор этого элемента
(2) минор элемента, умноженный на
(-1)i+j
(3) вычеркнутые строки и столбцы исходного определителя
Если ![math]() , то эти матрицы можно перемножать, если
, то эти матрицы можно перемножать, если
 , то эти матрицы можно перемножать, если
, то эти матрицы можно перемножать, если
(1)
p=r
(2)
m=n; p=r
(3)
m=n Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Если
, тогда
(1)
Δ=-3; Δx=-3; Δy=-3;
(2)
Δ=-3; Δx=-1; Δy=-1;
(3)
Δ=-3; Δx=1; Δy=1; Два вектора называются равными, если они совмещаются
(1) параллельным переносом
(2) любым преобразованием плоскости
(3) комбинацией поворота и параллельного переноса
Для того чтобы найти выражение
(a+b)(c+d), надо воспользоваться свойством
(1) скалярного произведения
(2) векторного произведения
(3) смешанного произведения
Для того чтобы найти выражение
(a+b)(c+d), надо воспользоваться свойством
(1) скалярного произведения
(2) векторного произведения
(3) смешанного произведения
Вычислить определитель
(1) 4
(2) 3
(3) 5
(4) 8
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Определитель равен
(1) произведению элементов любого столбца на свое алгебраическое дополнение
(2) сумме произведений элементов любого столбца или строки на их алгебраическое дополнение
(3) сумме произведений элементов столбца на алгебраические дополнения соответствующего столбца
Равенство
detAB=detA·detB выполняется
(1) для квадратных матриц
(2) для перестановочных матриц
(3) для прямоугольных матриц
(4) всегда
Система линейных уравнений имеет единственное решение, если
(1) главный определитель ее отличен от нуля
(2) количество уравнений равно количеству неизвестных
(3) ранг матрицы системы равен рангу расширенной матрицы
Два ненулевых вектора
a и b коллинеарны
(1) ..., если существует такое число θ, что
b=θ·a
(2) ..., следовательно существует такое число θ, что
b=θ·a
(3) тогда и только тогда, когда существует такое число θ, что
b=θ·a Даны два вектора ![math]() и
и ![math]() . Найти их скалярное произведение
. Найти их скалярное произведение
 и
и  . Найти их скалярное произведение
. Найти их скалярное произведение
(1) 10
(2) 4
(3) 8
(4) 6
(5) нет верного ответа
Даны два вектора ![math]() и
и ![math]() . Найти их скалярное произведение
. Найти их скалярное произведение
 и
и  . Найти их скалярное произведение
. Найти их скалярное произведение
(1) 10
(2) 4
(3) 14
(4) 16
(5) нет верного ответа
Какие вектора называют линейно зависимыми?
(1) если существуют такие числа
α1, α2 , ..., αк, не равные одновременно нулю, при которых выполняется α1а1 + α2а2 + ... + αкак = 0
(2) если существуют такие числа
α1, α2 , ..., αк, при которых выполняется α1а1 + α2а2 + ... + αкак = 0
(3) если существуют такие числа
α1, α2 , ..., αк, не равные нулю, при которых выполняется α1а1 + α2а2 + ... + αкак = 0 Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если строки в определителе заменить столбцами, то
(1) определитель не изменится
(2) определитель изменится по величине
(3) изменится по знаку
Присоединенная матрица состоит из
(1) миноров исходной матрицы
(2) алгебраических дополнений транспонированной матрицы
(3) из элементов, которые дополняют исходную матрицу до единичной, т.е.
A+B=E, где В – присоединенная матрица, А – исходная Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3; х4:
(1) 1; -1; 3; 4
(2) 2; 1; 1; 1
(3) 12,5; 1; -2,4; 3
(4) нет ответа
Найти координаты середины вектора ![math]() , если
, если
 , если
, если A(-1;2) и B(-3;4)
(1)
C(-2;3)
(2)
C(-4;6)
(3)
C(-1;3) Даны векторы
a = mi + 2j +3k, b = i + 3j -5k. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) -9
(4) -5
(5) нет верного ответа
Даны векторы
a = mi + 2j +3k, b = i + 3j -5k. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) -9
(4) -5
(5) нет верного ответа
Для доказательства линейной независимости векторов достаточно определить ...
(1) их не компланарность (для двух векторов)
(2) их не компланарность (для трех векторов)
(3) не коллинеарность (для двух векторов)
(4) не коллинеарность (для трех векторов)
Используя формулы Крамера, решить систему уравнений:
(1) (2; 3; 4)
(2) (1; 4; 6)
(3) (4; 1; 6)
(4) (3; 5; 2)
Если ![math]() тогда
тогда
 тогда
тогда
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для любого определителя при замене строк на столбцы
(1) величина определителя изменится на обратную
(2) величина определителя не изменится
(3) определитель изменит знак
Найти определитель матрицы методом звездочки
(1) 44
(2) 13
(3) 28
(4) 50
(5) нет верного ответа
Даны векторы
a(1;2) и b(3;k). При каком значении k угол между этими векторами будет равен 0°?
(1)
k=6
(2)
k=4
(3)
k=0
(4) нет правильного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 3i - j ; b = - i + 2j
(1) 0,2578
(2) -0,6875
(3) -0,7071
(4) 0,8695
(5) нет верного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 3i - j ; b = - i + 2j
(1) 0,2578
(2) -0,6875
(3) -0,7071
(4) 0,8695
(5) нет верного ответа
На плоскости для определения пространства необходимо задать
(1) два независимых вектора
(2) один вектор
(3) три независимых вектора
(4) столько векторов, сколько возможно
Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 5; 0; 2451
(2) 17;0; 3241
(3) 14; 0,3576
(4) 13; 0; 3412
Если ![math]() то
то
 то
то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Как изменяется определитель 3-го порядка, если первый столбец матрицы переставить на место последнего столбца, а остальные - передвинуть влево, сохраняя их расположение.
(1) изменит знак
(2) не изменится
(3) так делать нельзя
(4) станет равным нулю
Найти определитель матрицы методом звездочки
(1) 1
(2) 3
(3) 12
(4) -1
(5) нет правильного ответа
Координаты середины отрезка
AB, если A(x1;y1); B(x2;y2) находят по формуле
(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны векторы
a = (3,-5) и b = (4,-3). Найти координаты вектора c = a+2b
(1) (11;-11)
(2) (11;11)
(3) (7;-8)
(4) (7;8)
(5) нет верного ответа
Даны векторы
a = (3,-5) и b = (4,-3). Найти координаты вектора c = a+2b
(1) (11;-11)
(2) (11;11)
(3) (7;-8)
(4) (7;8)
(5) нет верного ответа
определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(1,1,2), а2(1,3,2), а3(4,3,2), С(1,0,0)
(1) невозможно
(2) (7, 4, 3)
(3) (0, -0,5; 0,75)
(4) (-1; 2; 0)
(5) возможно
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 9
(2) 8
(3) 4
(4) 7

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Как изменится определитель, если у всех его элементов изменить знак на противоположный? Отметьте верные утверждения.
(1) изменит знак, т.к. это обозначает умножение определителя на -1
(2) не изменится ничего
(3) изменит знак, если количество строк нечетное
(4) не изменится ничего, если количество строк четное
(5) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) 18
(2) 14
(3) 22
(4) 10
(5) нет правильного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 4i + 3j ; b = i – j
(1) 0,1245
(2) 0,1458
(3) 0,1587
(4) 0,1422
(5) нет верного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 4i + 3j ; b = i – j
(1) 0,1245
(2) 0,1458
(3) 0,1587
(4) 0,1422
(5) нет верного ответа
определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(2,3,2), а2(3,3,2), а3(4,4,4), С(0,0,1)
(1) невозможно
(2) (7, 4, 3)
(3) (0; -1; 0.75)
(4) (-1; 2; 0)
(5) возможно
Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (2; 3; 1; 7)
(2) (4; 5; 6; 3)
(3) (2; 1; 1; 1)
(4) (1; 3; 5; 7)
Значение ![math]() заключено
заключено
 заключено
заключено
(1) между 2 и 3
(2) между 3 и 4
(3) между 5 и 6
(4) между 6 и 7
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 100, 56, 44
(2) 100, 87, 13
(3) 86, 58, 28
(4) 87, 37, 50
(5) нет верного ответа
Даны векторы
a = (5; 12) и b = (0; 2). Найти скалярное произведение векторов (a—b)·b
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Даны векторы
a = (5; 12) и b = (0; 2). Найти скалярное произведение векторов (a—b)·b
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Найти площадь треугольника
АВС, если А[1,0,2]; B[2,1,2]; C[3,1,0]
(1) 2
(2) 4,2
(3) 1,5
(4) 5,1
Если ![math]() то
то
 то
то x= ?
(1) 2 или -2
(2) 3x
(3) 2
(4) 3
Указать правильное значение определителя:
(1)
3abc+(a3+b3+c3)
(2)
3abc-(a3+b3+c3)
(3) ![math]()

(4)
0 Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 15, 14, 1
(2) 15, 12, 3
(3) 14, 2, 12
(4) 14, 15, -1
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[1,0,1]; C[2,-1,-1]
(1) 2,33
(2) 1,73
(3) 1,54
(4) 1,98
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[1,0,1]; C[2,-1,-1]
(1) 2,33
(2) 1,73
(3) 1,54
(4) 1,98
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[5,5,2]; C[4,2,3], D[1,2,3]
(1) 3,48
(2) 5,35
(3) 6,13
(4) 4,12
Если ![math]() то
то
 то
то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Указать правильное значение определителя:
(1)
(a+b+c)2+b+d
(2)
(a-b-c)2+b+d
(3)
(a-b+c)2+b+d
(4)
c2+2*(d-ca-bc-ab)+b2+a2 Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) -5, -25, 18
(2) -7, -21, 14
(3) 1, -21, 22
(4) -5, -15, 10
(5) нет верного ответа
Периметр треугольника
АВС, где А[0, 2]; B[-3, -5]; C[-1, 3] равен примерно
(1) 17,3
(2) 15,8
(3) 17,1
(4) 16,3
(5) нет верного ответа
Найти периметр треугольника
АВС, если А[0, 2]; B[-3, -5]; C[-1, 3]
(1) 17,3
(2) 15,8
(3) 17,1
(4) 16,3
(5) нет верного ответа
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, 10
(2) нет, 4
(3) да, 1
(4) да, 0
Если ![math]() , то
, то
 , то
, то
(1) ![math]() ,
, ![math]() - целое
- целое
 ,
,  - целое
- целое
(2) ![math]() ,
, ![math]() - целое
- целое
 ,
,  - целое
- целое
(3) ![math]() ,
, ![math]() - целое
- целое
 ,
,  - целое
- целое
(4) нет правильного ответа
Указать определитель, который равен следующему:
(1)
(2)
(3)
Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 25, -192, 180
(2) -250, -192, 0
(3) -192, -205, -25
(4) нет верного ответа
Даны вершина тетраэдра
A(0;-2;5); B(6;6;0); C(3;-3;6); D(2;-1;3). Найти объем тетраэдра
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Даны вершина тетраэдра
A(0;-2;5); B(6;6;0); C(3;-3;6); D(2;-1;3). Найти объем тетраэдра
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Цена на телевизор увеличилась с 800 руб. до 1200 руб. На сколько процентов увеличилась цена?
(1) на 25%
(2) на 50%
(3) на 74%
(4) на 60%
Вычислить определители
(1) 4
(2) 1
(3) -8
(4) нет верного ответа
Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 10, -21, 5
(2) -15, 1, 0
(3) 0, 0, -16
(4) нет верного ответа
К телу приложена сила
F(0, 0, 12), под действием которой тело перемещается из точки А(10, 0, 0) в точку В(1, 4, -3). Найти работу, совершаемую силой по перемещению тела из точки А в точку В
(1) 20
(2) 25
(3) 30
(4) 36
(5) нет верного ответа
К телу приложена сила
F(0, 0, 12), под действием которой тело перемещается из точки А(10, 0, 0) в точку В(1, 4, -3). Найти работу, совершаемую силой по перемещению тела из точки А в точку В
(1) 20
(2) 25
(3) 30
(4) 36
(5) нет верного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()
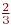
(3) ![math]()
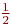
Найти определитель матрицы по теореме о разложении определителя по элементам второго столбца. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 6, 0, 0
(2) 0, 6, 0
(3) 0, 0, 6
(4) нет верного ответа
Если из 68 вычесть 37, то получится
(1) 35
(2) 31
(3) 33
(4) 32
(5) нет правильного ответа.
Вычислить детерминант
(1) 2
(2) 4
(3) 6
(4) 8
(5) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если ![math]()
х=100, то чему равен 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить детерминант
(1) 2121
(2) -1022
(3) 1020
(4) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)

(1) 0,12;
(2) 1,2;
(3) 0,012;
(4) нет правильного ответа.
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) прямая
(2) спираль
(3) окружность
(4) точка
Заданы точки
А(0,0) и В(2,1) длина отрезка АВ равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
Центр окружности радиуса 3 находится в точке с координатами
(0,5). Сколько раз окружность пересекает координатные оси
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно
5!?
(1) 20
(2) 60
(3) 80
(4) 120

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если старший сын вдвое моложе матери и втрое старше брата, то младший брат моложе матери в:
(1) 4 раза
(2) 6 раз
(3) 8 раз
(4) нет правильного ответа
Если
a > b, b > c, то тогда c должно быть:
(1) меньше
а
(2) равно
а
(3) больше
а Даны две прямые
y+x=2 и y-x=1. Эти прямые
(1) параллельны
(2) перпендикулярны
(3) пересекаются под углом в
45° Прошло 2/3 часа, что составило:
(1) 45 минут
(2) 40 минут
(3) 50 минут
Во сколько раз 64 больше 48:
(1) в 1,5 раза
(2) в ![math]() раза
раза
 раза
раза
(3) 1,2 раза
Выбрать самое большое число:
(1) ![math]()

(2) ![math]()
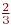
(3) ![math]()

(4) ![math]()

Если две строки в определителе поменять местами, то определитель
(1) изменится по величине
(2) изменит знак
(3) не изменится
Количество строк и количество столбцов в матрице
(1) совпадают
(2) равно количеству строк и столбцов соответствующей матрицы
(3) не совпадают
(4) могут не совпадать
Дана система
.
Детерминантом этой системы будет число, равное
(1) -1
(2) 7
(3) -5
(4) 5
Элементарными преобразованиями линейной системы называют
(1) перестановку любых двух уравнений
(2) умножение любого уравнения на число, отличное от нуля
(3) любые преобразования, которые переводят линейную систему в эквивалентную
Если ϕ - градусная мера угла между векторами
а и с, то
(1)
0 ≤ ϕ ≤ 180°
(2)
0 ≤ ϕ < 360°
(3)
-90° ≤ ϕ ≤ 90° Даны векторы
a(1;0;2) и b(3;4;0). Чему должно быть равно векторное произведение [a,b]?
(1)
(2)
(3)
(4) ни один из предложенных
Даны векторы
a(1;0;2) и b(3;4;0). Чему должно быть равно векторное произведение [a,b]?
(1)
(2)
(3)
(4) ни один из предложенных
Определите, является ли числовым полем следующее множество:
1 2 3 4 ... 100 101 ... М М+1 ...
(1) да
(2) нет
В обычном трехмерном пространстве геометрических векторов подпространствами будут являться ...
(1) совокупность его элементов
R1, которая сама является линейным пространством
(2) совокупность его элементов
R1, которая сама является линейным пространством относительно введенных в R операций сложения и умножения на число
(3) множества векторов на всех плоскостях и всех прямых, проходящих через начало координат
(4) подпространства
R1, размерность которого должна быть меньше или равна размерности пространства R Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) 2
(3) -8
(4) -13
(5) ни один из данных ответов
Элементами матрицы могут быть
(1) только числа
(2) только функции
(3) только матрицы
(4) числа, функции, матрицы
Систему линейных уравнений, имеющую хотя бы одно решение называют
(1) совместной
(2) не совместной
(3) линейной
Свободными неизвестными называют
(1) неизвестные, которые могут быть выражены как линейная комбинация главных
(2) неизвестные, через которые могут быть выражены главные
(3) то количество неизвестных, которое остается в системе при приведении ее к диагональному виду
Основное свойство сложения векторов записывают как
(1) если
a=a1 и b=b1, то a+b=a1+b1
(2)
a+0=0+a=a; a+b=b+a
(3)
(a+b)+c=a+(b+c); a+b=b+a Угол ϕ между векторами
a и b находится по формуле
(1) ![math]()

(2) ![math]()

(3) ![math]()

Угол ϕ между векторами
a и b находится по формуле
(1) ![math]()

(2) ![math]()

(3) ![math]()

Определите, является ли данное множество линейным пространством:
... -(М+1) -М ... -101 -100 ... -4 -3 -2 -1 0 1 2 3 4 ... 100 101 ... М М+1 ...
(1) да
(2) нет
Если в пространстве нельзя задать длину, то такое пространство называют...
(1) аффинным
(2) метрическим
(3) независимым
(4) евклидовым
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Порядком определителя назовем
(1) количество строк
(2) количество столбцов
(3) количество строк или столбцов
Если матрицы
А и В коммутативные, то обязательно выполняется равенство
(1)
detAB=detAdetB
(2)
AB=BA
(3)
(A+B)C=AC+BC Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Если ранг основной матрицы равен рангу расширенной матрицы, то
(1) система линейных уравнений совместна и имеет единственное решение
(2) система линейных уравнений совместна и может иметь как одно, так и множество решений
(3) система линейных уравнений совместна, если столбец свободных членов не нулевой
Длиной или модулем вектора называется
(1) расстояние между началом и концом вектора
(2) модуль разности ординат начала и конца вектора
(3) модуль разности абсцисс начала и конца вектора
Геометрический смысл смешанного произведения векторов
a; b; c заключается в том, что
(1) численно (по модулю) оно равно объему параллелепипеда, построенного на этих векторах как на сторонах
(2) оно равно объему параллелепипеда, построенного на этих векторах как на сторонах
(3) численно (по модулю) оно равно шести объемам пирамиды, построенной на этих векторах как на сторонах при вершине пирамиды
Геометрический смысл смешанного произведения векторов
a; b; c заключается в том, что
(1) численно (по модулю) оно равно объему параллелепипеда, построенного на этих векторах как на сторонах
(2) оно равно объему параллелепипеда, построенного на этих векторах как на сторонах
(3) численно (по модулю) оно равно утроенному объему пирамиды, построенного на этих векторах как на сторонах при вершине пирамиды
Определите какое из приведенных множеств является отображаемым по отношению к исходному (данному):
1 4 9 16 25
(1) 1 2 3 4 5
(2) -1 -2 3 -3 -5
(3) 1 -1 2 -2 3 -3
(4) -1 -2 3 -3 -5 1 2 3 4 5
Если некоторая величина может быть охарактеризована своими значением и направлением, то такую величину называют...
(1) базисной
(2) векторной
(3) скалярной
(4) положительной или отрицательной
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Выписать все алгебраические дополнения определителя ![math]()

(1) 1; 2; 3; 4
(2) 1; 2; -3; 4
(3) -1; -2; -3; -4
(4) 2; 2; -3; 4
Если матрица
А имеет обратную, то она называется
(1) не особенной
(2) особенной
(3) квадратной
Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Если при преобразовании системы линейных уравнений с целью поиска решения система приводится к нижнему треугольному виду, то метод, используемый в этом случае называется
(1) метод неопределенных коэффициентов
(2) метод последовательного исключения неизвестных
(3) метод множителей
(4) данный метод здесь не перечислен
Дана точка
M(2;-4;3) в прямоугольной декартовой системе координат. Определить координаты точки, симметричной точке М относительно начала координат.
(1) (-2;4;3)
(2) (-2;4;-3
(3) (2;4;-3
(4) ни один из предложенных
Геометрический смысл векторного произведения двух векторов заключается в том, что
(1) векторное произведение векторов
a и b равно площади параллелограмма, построенного на этих векторах как на сторонах
(2) модуль векторного произведения векторов
a и b равен площади треугольника, построенного на этих векторах как на сторонах
(3) модуль векторного произведения векторов
a и b равен площади параллелограмма, построенного на этих векторах как на сторонах Геометрический смысл векторного произведения двух векторов заключается в том, что
(1) векторное произведение векторов
a и b равно площади параллелограмма, построенного на этих векторах как на сторонах
(2) модуль векторного произведения векторов
a и b равен площади треугольника, построенного на этих векторах как на сторонах
(3) модуль векторного произведения векторов
a и b равен площади параллелограмма, построенного на этих векторах как на сторонах Вычислить определитель
(1) 8
(2) 2
(3) -3
(4) 1
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Определитель третьего порядка имеет
(1) 6 миноров первого порядка
(2) 9 миноров второго порядка
(3) 3 минора первого порядка
(4) 8 миноров второго порядка
Если
A=(-1)B, то матрица А называется
(1) обратимой
(2) симметричной матрице
В
(3) противоположной матрице
В Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3:
(1) 2; 3; 5
(2) 2; -2; 3
(3) 6; 20; 6
(4) нет ответа
Если
, то один из этапов решения системы по методу Гаусса выглядит
(1)
(2)
(3)
Пусть даны две точки
A(8;-5) и B(0;3). Определить расстояние AB между данными точками
(1) ![math]()

(2) ![math]()

(3) 64
(4) 8
Даны два вектора
a=(1;-2;2) и b=(2;-2;-1). Найти значения выражения 2a2-4ab+5b2
(1) 47
(2) 13
(3) 18
(4) 14
(5) нет верного ответа
Если равенство
α1а1 + α2а2 + ... + αкак = 0 выполнимо лишь при всех αi = 0, то векторы а1, а2, ..., ак называются...
(1) линейно зависимыми
(2) линейно независимыми
Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если к элементам одного столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки) то
(1) определитель увеличится
(2) определитель не изменится
(3) так делать нельзя
Если
A* - присоединенная матрица к матрице А, то
(1)
AA*=E
(2)
AA*=(detA)E
(3)
AA=A-1 Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3; х4:
(1) 1; 1; 3; 4
(2) 2; 1; 1; 1
(3) 12,5; 1; -2,4; 3
(4) нет ответа
Метод Крамера в решении систем линейных уравнений заключается в
(1) вычислении определителей
(2) приведение системы уравнений к треугольному виду
(3) умножении слева на обратную матрицу
Длина вектора ![math]() , если
, если
 , если
, если A(a1;a2) и B(b1;b2) вычисляется по формуле
(1)
(b2-a2)+(b1-a1)
(2)
(b2-a2)2+(b1-a1)2
(3) ![math]()

Найти скалярное произведение векторов
a = (2, 3, 4) и b = (5, 6, 0), а также косинус угла между этими векторами
(1) 20, 0,7615
(2) 9, 0,3567
(3) 29, 0,6657
(4) 28, 0,6657
(5) нет верного ответа
Найти скалярное произведение векторов
a = (2, 3, 4) и b = (5, 6, 0).
(1) 20
(2) 9
(3) 29
(4) 28
Если один из векторов
а1, а2, ..., ак линейно выражается через остальные, то все эти векторы в совокупности ...
(1) линейно зависимы
(2) линейно независимы
(3) образуют базис
Используя формулы Крамера, решить систему уравнений:
(1) (1; 0; 5)
(2) (0; 2; 3 )
(3) (4; 3; 1)
(4) (2; 0; 3)
Если ![math]() тогда
тогда
 тогда
тогда
(1)
(2) ![math]()

(3) ![math]()

Дан определитель ![math]() . Две строки в определителе пропорциональны, поэтому
. Две строки в определителе пропорциональны, поэтому
 . Две строки в определителе пропорциональны, поэтому
. Две строки в определителе пропорциональны, поэтому
(1) общий множитель 3 можно вынести за определитель
(2) определитель вычислить нельзя
(3) определитель равен нулю
Найти определитель матрицы методом звездочки
(1) 6
(2) 10
(3) 0
(4) -2
(5) нет верного ответа
Дана точка
M(-2;-4;3) в прямоугольной декартовой системе координат. Определить координаты точки, симметричной точке М относительно начала координат
(1) (-2;4;3)
(2) (-2;4;-3)
(3) (2;4;-3)
(4) ни один из предложенных
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = -2i - 4j ; b = 4i + 2j
(1) 0,8
(2) -0,8
(3) 0,5
(4) 0,6
(5) нет верного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = -2i - 4j ; b = 4i + 2j
(1) 0,8
(2) -0,8
(3) 0,5
(4) 0,6
(5) нет верного ответа
Базисом
n-мерного пространства называют...
(1) множество линейно независимых векторов
(2) совокупность
n линейно независимых единичных векторов n-мерного пространства
(3) cовокупность попарно ортогональных векторов
(4) сколь угодно много линейно независимых векторов
Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 28; 0,6657
(2) 30; 0,5543
(3) 19; 0,4321
(4) 13; 0,5234
Если ![math]() тогда
тогда
 тогда
тогда
(1) ![math]()

(2) ![math]()

(3) ![math]()

Как изменяется определитель 4-го порядка, если первый столбец его переставить на место последнего, а остальные - передвинуть влево, сохраняя их расположение. Показать на примере определителей.
(1) изменит знак
(2) не изменится ничего
(3) так делать нельзя
(4) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) 4
(2) 6
(3) 8
(4) 10
(5) нет правильного ответа
Дана точка
M(1;3;-7) в прямоугольной декартовой системе координат. Определить координаты точки К, симметричной с точкой М относительно координатной плоскости X0Y
(1)
K(-1;-3;-7)
(2)
K(-1;-3;7)
(3)
K(1;3;7)
(4)
K(1;-3;7) Найти скалярное произведение векторов
a = (4; 5) и b = (7; -4)
(1) 9
(2) 8
(3) 7
(4) 6
(5) нет верного ответа
Найти скалярное произведение векторов
a = (4; 5) и b = (7; -4)
(1) 9
(2) 8
(3) 7
(4) 6
(5) нет верного ответа
определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(21,0,2), а2(0,1,2), а3(4,3,2), С(5,1,3)
(1) невозможно
(2) (6/23; 125/92; -11/92)
(3) (0,2; 0,25; -0,1)
(4) (1,6; 1; -0,8)
(5) возможно
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 1
(2) 6
(3) 9
(4) 5

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти определитель матрицы методом звездочки
(1) 33
(2) 29
(3) 12
(4) 30
(5) нет правильного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 4i - 5j ; b =3 i - 2 j
(1) 0,9529
(2) 0,9125
(3) 0,9595
(4) 0,9345
(5) нет верного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 4i - 5j ; b =3 i - 2 j
(1) 0,9529
(2) 0,9125
(3) 0,9595
(4) 0,9345
(5) нет верного ответа
определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(1,2,2), а2(5,2,5), а3(0,1,0), С(2,6,1)
(1) (-1,4; 2,3; -0,65)
(2) (0,2; 0,25; -0,1)
(3) невозможно
(4) возможно
(5) (-1; 0,6; 6,8)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 5 и 6
(2) 6 и 7
(3) 7 и 8
(4) 8 и 9
Как изменится определитель второго порядка, если из первой строки вычесть первую строку, а из второй строки вычесть прежнюю первую строку?
(1) станет равным нулю
(2) изменит знак
(3) не изменится
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) -19, -25, 6
(2) -19, -29, 10
(3) -25, -25, 0
(4) 25, -25, 50
(5) нет верного ответа
Даны векторы
a = 6i - mj + 2k, b = 3i + 2j + k. При каком значении m они будут параллельны?
(1) 2
(2) 4
(3) -2
(4) -4
Даны векторы
a = 6i - mj + 2k, b = 3i + 2j + k. При каком значении m они будут параллельны?
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,0,2]; B[2,1,2]; C[3,1,0]
(1) 6
(2) 4
(3) 7
(4) 3
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет решения
Указать правильное значение определителя:
(1)
cdflv
(2)
xyuzv
(3)
ayzuv
(4)
ghkua
(5) нет ответа
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 6, 2, 4
(2) 6, -4, 10
(3) 2, -6, 8
(4) 0, -6, 6
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[0,1,2]; B[2,4,1]; C[3,2,2], D[1,5,3]
(1) 4
(2) 8
(3) 6
(4) 3
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[0,1,2], B[2,4,1], C[3,2,2], D[1,5,3]
(1) 4
(2) 8
(3) 3
(4) 6
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[4,3,2]; C[4,5,3], D[5,5,6]
(1) 4,56
(2) 1,32
(3) 2,39
(4) 5,76
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) нет правильного ответа
(4) ![math]()

Указать правильное значение определителя:
(1)
=2abc(a+b+c)2
(2)
=2abc(a+b+c)3
(3)
=2(a+b)(b+c)(a+b+c)2
(4)
=2((a+b)(b+c)(a+c))2 Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 75, 42, 33
(2) 71, 42, 29
(3) 75, 63, 12
(4) 72, 42, 30
(5) нет верного ответа
Найти периметр треугольника
АВС, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 11,5
(2) 10,9
(3) 10,3
(4) 12,0
(5) нет верного ответа
Найти периметр треугольника
АВС, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 11,5
(2) 10,9
(3) 10,3
(4) 12,0
(5) нет верного ответа
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, 6
(2) нет, 7
(3) нет, -21
(4) да, 4
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Указать правильное значение определителя:
(1)
...=1
(2)
...=0
(3) ![math]()

Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 45, -35, -20
(2) -70, -35, 45
(3) -36, 0, 30
(4) нет верного ответа
Вычислить, какую работу производит сила ![math]() , когда точка, к которой эта сила пролажена перемещается из положения
, когда точка, к которой эта сила пролажена перемещается из положения
 , когда точка, к которой эта сила пролажена перемещается из положения
, когда точка, к которой эта сила пролажена перемещается из положения M(1;-2;3) в положение N(5;-6;1). Указание: Здесь необходимо вспомнить, что работа это есть скалярное произведение вектора силы на вектор перемещения
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Вычислить, какую работу производит сила ![math]() , когда точка, к которой эта сила пролажена перемещается из положения
, когда точка, к которой эта сила пролажена перемещается из положения
 , когда точка, к которой эта сила пролажена перемещается из положения
, когда точка, к которой эта сила пролажена перемещается из положения M(1;-2;3) в положение N(5;-6;1). Указание: Здесь необходимо вспомнить, что работа это есть скалярное произведение вектора силы на вектор перемещения
(1) 20
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Цена на книгу увеличилась с 6 руб. до 8 руб. На сколько процентов увеличилась цена книги?
(1) на 10%
(2) на 22%
(3) на 32%
(4) на 33,3 %
Вычислить определители
(1) 0
(2) -3
(3) 1
(4) нет верного ответа
Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) -36, 0, 30
(2) 0, 0, -6
(3) -6, 0, 0
(4) нет верного ответа
Даны векторы
a = 3i - mj - 4k, b = 2i + 2j - 3k. При каком значении m они будут перпендикулярны?
(1) -9
(2) 5
(3) 9
(4) -5
(5) нет верного ответа
Даны векторы
a = 3i - mj - 4k, b = 2i + 2j - 3k. При каком значении m они будут перпендикулярны?
(1) -9
(2) 5
(3) 9
(4) -5
(5) нет верного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Вычислить определители
(1) 66
(2) -144
(3) 210
(4) нет правильного ответа
Найти определитель матрицы по теореме о разложении определителя по элементам второго столбца. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 16, 120, 42
(2) 4, 120, 54
(3) -15, 12, 21
(4) нет верного ответа
Если из 94 вычесть 39, то в остатке будет
(1) 55;
(2) 56;
(3) 54;
(4) 45.
Вычислить детерминант
(1) 2
(2) 4
(3) 6
(4) 8
(5) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если ![math]()
х=64, то чему равен 
(1) 3
(2) 4
(3) 5
(4) 6
(5) нет правильного ответа
Вычислить детерминант
(1) 231
(2) 448
(3) 123
(4) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) прямая
(2) 2-х лепестковая роза
(3) 4-х лепестковая роза
(4) окружность
(5) спираль
Заданы две точки
А(1,1) и В(4,5). Расстояние между проекциями этих точек на ось 0х равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Центр окружности радиуса 1,5 находится в точке
(1,1). Сколько раз окружность пересекает координатные оси?
(1) 1 раз
(2) 2 раза
(3) 3 раза
(4) 4 раза
(5) ни одного раза
Чему равно ![math]() ?
?
 ?
?
(1) 20
(2) 60
(3) 80
(4) 120

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если отец втрое старше сына и вдвое старше дочери, то во сколько раз брат младше сестры?
(1) брат старше сестры
(2) в 3 раза
(3) 1,5 раза
(4) в 2/3 раза
Даны две прямые
y+x=3 и 2y+2x=4. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
Прошло 0,2 часа, что составило:
(1) 6 минут
(2) 12 минут
(3) 15 минут
Во сколько раз 39 больше 26?
(1) в 1,5 раза
(2) в 0,5 раза
(3) в 2/3 раза
Выбрать наименьший результат:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Определитель второго порядка это
(1) число, равное
a11·a22-a12·a21
(2) число, равное
a12·a21-a11·a22
(3) число, равное
a11+a12+a21+a22 Если все элементы строки матрицы умножить на какое-либо число, то
(1) определитель матрицы умножатся на это число
(2) определитель матрицы не изменится
(3) определитель матрицы увеличится в
n·m раз, где n - количество элементов в строке, m - число, на которое умножаем Система называется несовместной, если
(1) имеет единственное решение
(2) имеет любое количество решений
(3) не имеет решения
Для того, чтобы система линейных уравнений была бы совместной
(1) необходимо и достаточно, чтобы ранг основной матрицы
А был равен рангу ее расширенной матрицы В, то есть Rg A = Rg B
(2) необходимо, чтобы ранг основной матрицы
А был равен рангу ее расширенной матрицы В, то есть Rg A = Rg B
(3) достаточно, чтобы ранг основной матрицы
А был равен рангу ее расширенной матрицы В, то есть Rg A = Rg B Даны точки ![math]()
A(5;-2) и B(-7;3). Найти длину вектора 
(1) 5
(2) 13
(3) 7
(4) 1
(5) ни один из предложенных
Смешанное произведение трех векторов
a(1;2;3); b(0;3;-1;); c(-1;0;2) равно
(1) (0;5;0)
(2) (0;0;-6)
(3)
Смешанное произведение трех векторов
a(1;2;3); b(0;3;-1;); c(-1;0;2) равно
(1) (0;5;0)
(2) (0;0;-6)
(3)
Определите, является ли числовым полем следующее множество:
0 1 2 3 4 ... 100 101 ... М М+1 ...
(1) да
(2) нет
Совокупность всех решений однородной системы уравнений с рангом
r является...
(1) фундаментальной
(2) линейным
(n - r)-мерным подпространством в n-мерном арифметическом пространстве R
(3) системой независимых решений однородной системы уравнений
(4) фундаментальной системой решений
Найти производную функции
f(x) в точке х = -1:
(1) 3
(2) 2
(3) -3
(4) -13
(5) ни один из данных ответов.
Если строки определителя поменять со столбцами, то эта операция называется
(1) транспонированием
(2) обращением
(3) не имеет специального названия
Элементы
аij, из которых составлена матрица называются
(1) коэффициентами матрицы
(2) элементами данной матрицы
(3) элементами таблицы
Решением системы называется любая совокупность чисел, которая
(1) удовлетворяет хотя бы одному линейных уравнений
(2) удовлетворяет практически всем уравнений системы
(3) обращает все уравнения системы при подстановке в истинные тождества
Если ранг основной матрицы меньше ранга расширенной матрицы, то
(1) система совместна
(2) система имеет бесконечное множество решений
(3) система не совместна, то есть решений не имеет
Найти координаты середины отрезка
MN, если M(3,11); N(7,25)
(1) (5,18)
(2) (5,7)
(3) (2,7)
(4) (2,18)
Скалярным произведением двух ненулевых векторов
a и b называется
(1) вектор, длина которого равна произведению длин указанных векторов
(2) число, равное произведению длин этих векторов на косинус угла между ними
(3) число, равное произведению длин этих векторов на синус угла между ними
Скалярным произведением двух ненулевых векторов
a и b называется
(1) вектор, длина которого равна произведению длин указанных векторов
(2) число, равное произведению длин этих векторов на косинус угла между ними
(3) число, равное произведению длин этих векторов на синус угла между ними
Определите, является ли данное множество линейным пространством: Множество всех чисел
(1) да
(2) нет
Если определена матрица перехода от одного независимого базису к другому, то тогда...
(1) не важно от какого типа пространства в какое переходить. Матрица перехода определяет данное преобразование координат однозначно
(2) важно, чтобы это были однотипные базисы
(3) не важно от какого типа пространства в какое переходить. Однако обратное преобразование тогда будет невозможно
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если все элементы столбца в определителе умножить на какое-либо число, отличное от нуля, то
(1) определитель умножится на это число
(2) так делать нельзя
(3) определитель станет равным
(mn)D, где m - число, n - количество элементов столбца, D - определитель Матрицы
А и В назовем равными, если
(1) они имеют одинаковые размеры
(2) каждому элементу матрицы
А можно найти равный в матрице В
(3) для всех элементов указанных матриц выполняется равенство
aij=bij Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Решение ![math]() называется
называется
 называется
называется
(1) формулами Крамера
(2) формулами Гаусса
(3) формулами определителей
Нулевой вектор имеет направление
(1) совпадающее с положительным направлением оси абсцисс
(2) совпадающее с положительным направлением оси ординат
(3) не имеет определенного направления
Найти значение выражения
(a+b)2, если известно, что (a^b)=0°, |a|=3; |b|=5
(1) 64
(2) 34
(3) 16
(4) нет правильного ответа
Найти значение выражения
(a+b)2, если известно, что (a^b)=0°, |a|=3; |b|=5
(1) 64
(2) 34
(3) 16
(4) нет правильного ответа
Определите какое из приведенных множеств является отображаемым по отношению к исходному (данному): одежда
(1) пальто платье костюм
(2) тапочки носки чулки кофта
(3) брюки юбка галстук
Верно ли утверждение "Любой базис, независимо от его размерности и первоначальных значений, можно привести к ортонормированному"?
(1) верно
(2) нет
(3) верно, если добавить условие ортогональности базиса
(4) для того, чтобы это утверждение было верным необходимо, чтобы базис определял евклидово пространство
(5) верно. Но, если базис определял не евклидово пространство, то сначала надо осуществить преобразование заданного базиса в евклидовый, а затем провести его нормирование
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если столбцы в определителе поменять местами, то определитель
(1) изменит знак
(2) изменит величину
(3) не изменится
Основным свойством обратной матрицы является
(1)
A·A-1=A-1·A=E
(2)
AT=A-1
(3)
ABA-1=A-1BA Ответьте на вопрос: совместна ли система уравнений?
(1) совместна
(2) не совместна
(3) нельзя ответить на этот вопрос
Если
, тогда
(1)
Δ=-5; Δx=10; Δy=20;
(2)
Δ=-5; Δx=-20; Δy=-10;
(3)
Δ=-5; Δx=-10; Δy=20; Дан вектор
a(-0;-5;0). Вычислить значение |-3a|.
(1) 15
(2) 8
(3) (0;15;0)
(4) ни один из предложенных
Какое из следующих тождеств является свойством скалярного произведения векторов?
(1)
ab=ba
(2)
α(βa)=(αβ)a
(3)
ab=-ba Какое из следующих тождеств является свойством скалярного произведения векторов?
(1)
ab=ba
(2)
α(βa)=(αβ)a
(3)
ab=-ba Вычислить определитель
(1) -58
(2) 60
(3) 54
(4) -50
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если в определителе две строки пропорциональны, то
(1) определитель - четное число
(2) определитель равен нулю
(3) определитель больше нуля
Если в некоторой матрице
А поменять местами строки и столбцы, то полученную матрицу называют по отношению к исходной
(1) симметрической
(2) перестановочной
(3) транспонированной
Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3:
(1) 2; -2; 3
(2) 2; 3; 5
(3) 6; 20; 6
(4) нет ответа
Если
, то такая система
(1) не совместна
(2) имеет единственное решение
(3) имеет множество решений
Единичным вектором называется вектор, длина которого
(1) принята за единицу измерения длины
(2) равна 1 см
(3) равна 1 м
Даны векторы
a = 3i - mj - 4k, b = 2i + 2j - 3k. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) -9
(4) -5
(5) нет верного ответа
Даны векторы
a = 3i - mj - 4k, b = 2i + 2j - 3k. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) -9
(4) -5
(5) нет верного ответа
Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Дан определитель ![math]() . Минор
. Минор
 . Минор
. Минор D23 этого определителя будет равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если
RgA<min(m,n), то такая матрица
(1) содержит не меньше двух зависимых строк (столбцов)
(2) содержит две зависимые строки (столбца)
(3) определитель матрицы равен нулю
Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3; х4:
(1) -1; 3; 0; 9
(2) 20,5; -10; -5,5; 49
(3) -1; 0; 3; 6
(4) нет ответа
Метод Гаусса в решении систем линейных уравнений заключается в
(1) вычислении определителей
(2) приведение системы уравнений к треугольному виду
(3) умножении слева на обратную матрицу
Пусть даны две различные точки
A(3;0) и B(-2;5). Определить координаты точки М, которая делит отрезок AB в отношении λ=1.
(1) ![math]()

(2)
M(1;5)
(3)
M(0;3)
(4)
M(1;2)
(5) нет правильного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 3i + 4j ; b = i - 7j
(1) 0,2578
(2) -0,6875
(3) -0,7071
(4) 0,8695
(5) нет верного ответа
Найти косинус угла между векторами
a и b, заданными в координатной форме: a = 3i + 4j ; b = i - 7j
(1) 0,2578
(2) -0,6875
(3) -0,7071
(4) 0,8695
(5) нет верного ответа
Линейное пространство называется
n - мерным, если...
(1) оно составлено из
n однородных элементов
(2) если в нем можно найти
n линейно независимых векторов и любой набор из n+1 вектора линейно зависим
(3) если в нем можно найти не меньше, чем
n линейно независимых векторов Используя формулы Крамера, решить систему уравнений:
(1) (-2; -1; 4)
(2) (2; -4; 3)
(3) (-2; 1; -1)
(4) (1; -2; 3)
Если ![math]() тогда
тогда
 тогда
тогда
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти определитель матрицы методом звездочки
(1) 20
(2) -20
(3) 60
(4) -60
(5) нет верного ответа
Даны точки ![math]()
A(5;-2) и B(-7;3). Найти длину вектора 
(1) 5
(2) 3
(3) 7
(4) 1
(5) ни один из предложенных
Найти скалярное произведение векторов
(a - b)·a, если даны a = (5, 12) и b = (1,2)
(1) 100
(2) 120
(3) 160
(4) 140
(5) нет верного ответа
Найти скалярное произведение векторов
(a - b)·a, если даны a = (5, 12) и b = (1,2)
(1) 100
(2) 120
(3) 160
(4) 140
(5) нет верного ответа
Пространство называют бесконечномерным, а если в нем можно найти ...
(1) вектор
х линейного n-мерного пространства, который можно представить, и притом единственным образом, в виде линейной комбинации векторов базиса
(2) сколь угодно много базисных векторов, через которые могут быть выражены любые другие векторы, определяемые в данном базисе
(3) конечное множество линейно независимых векторов
(4) сколь угодно много линейно независимых векторов
Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 12; 0,7653
(2) 10; 0,1524
(3) 1; 4,0452
(4) 14; 0,8367
Если ![math]() то
то
 то
то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Как изменится определитель, если его строки написать в обратном порядке? Отметьте верные утверждения.
(1) изменит знак, если количество перестановок нечетное
(2) не изменится ничего, если количество перестановок четное
(3) не изменится ничего, если количество перестановок нечетное
(4) изменит знак, если количество перестановок четное
(5) так делать нельзя
(6) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) 10
(2) -10
(3) 18
(4) -18
(5) нет правильного ответа
Найти координаты вектора
a-b, если a(1;21;-7) и b(0;30;-2).
(1) (1;9;-9)
(2) (1;-9;-9)
(3) (1;-9;-5)
(4) (-1;9;5)
Найти скалярное произведение векторов
a = (3; 7) и b = (3; - 1)
(1) 9
(2) 3
(3) 0
(4) 2
(5) нет верного ответа
Найти скалярное произведение векторов
a = (3; 7) и b = (3; - 1)
(1) 9
(2) 3
(3) 0
(4) 2
(5) нет верного ответа
Определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(7,5,1), а2(4,4,4), а3(0,2,1), С(1,1,4)
(1) (-0.6; 1.3; -0.6)
(2) (0,2; 0,25; -0,1)
(3) (1,6; 1; -0,8)
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 1,3
(2) 5
(3) 3,2
(4) 4,5
Вычислить значение выражения ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) 4
(2) 6
(3) 8
(4) 10
(5) нет правильного ответа
Даны векторы
a =(1, 2) и b=(5, 1). Найти координаты вектора c = 2a - 3b
(1) (13; 1)
(2) (-13; 1)
(3) (-13; -1)
(4) (13; -1)
(5) нет верного ответа
Даны векторы
a =(1, 2) и b=(5, 1). Найти координаты вектора c = 2a - 3b
(1) (13; 1)
(2) (-13; 1)
(3) (-13; -1)
(4) (13; -1)
(5) нет верного ответа
Определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(5,2,4), а2(3,4,5), а3(7,4,3), С(1,1,2)
(1) (7/26; 15/52; -9/52)
(2) (-1; 2; 0)
(3) (1,6; 1; -0,8)
Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (1; -1; 3; 4)
(2) (0; -3; -4; -3)
(3) (1; 4; 5; 6)
(4) (1; -3; -5; 21)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 4 и 5;
(2) 6 и 7;
(3) 7 и 8.
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 200, 180, 20
(2) 200, 220, -20
(3) 260, 200, 60
(4) 200, 260, -60
(5) нет верного ответа
Найти площадь треугольника
АВС, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 3,8
(2) 4,9
(3) 4,2
(4) 3,6
(5) нет верного ответа
Найти площадь треугольника
АВС, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 3,8
(2) 4,9
(3) 4,2
(4) 3,6
(5) нет верного ответа
Найти периметр треугольника, если
А[1,0,2]; B[2,1,2]; C[3,1,0] его вершины
(1) 3,2
(2) 5,31
(3) 8,22
(4) 6,65
Если
1/x+2=x+1/x то x равно:
(1)
0
(2)
1
(3)
2
(4) нет правильного ответа
Указать правильное значение определителя:
(1)
2a-8b+c+5d
(2)
-2a+8b-c+5d
(3)
2a+8b+c+5d
(4) нет ответа
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 39, 29, 10
(2) 29, 39, -10
(3) 39, 21, 18
(4) 21, 39, -18
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[3,5,6]; C[2,-1,-1]
(1) 13,42
(2) 15,3
(3) 13,78
(4) 14,9
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[3,5,6]; C[2,-1,-1]
(1) 13,42
(2) 15,3
(3) 13,78
(4) 14,9
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[5,2,2]; C[4,6,4], D[6,4,4]
(1) 2,34
(2) 3,12
(3) 4,12
(4) 6,31
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) нет правильного ответа
Указать правильное значение определителя:
при
a2+b2+c2=1
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 36, 32, 4
(2) 36, 30, 6
(3) 30, 22, 8
(4) 30, 20, 10
(5) нет верного ответа
Даны векторы ![math]() и
и ![math]() . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах
 и
и  . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах
(1) 15,4
(2) 14,14
(3) 10,3
(4) 16,3
(5) нет верного ответа
Даны векторы ![math]() и
и ![math]() . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах
 и
и  . Найти площадь параллелограмма, построенного на этих векторах
. Найти площадь параллелограмма, построенного на этих векторах
(1) 15,4
(2) 14,14
(3) 10,3
(4) 16,3
(5) нет верного ответа
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, 1
(2) да, 4
(3) нет, -3
(4) нет, 5
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Указать правильное значение определителя:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) -6, 0, 0
(2) 0, 6, 0
(3) 0, 0, -6
(4) нет верного ответа
Под действием силы
F = 2i - 4j тело из точки А(2,3,-1) переместилось в точку В(1, 1, 1). Найти работу указанной силы
(1) 20
(2) 6
(3) 12
(4) 10
(5) нет верного ответа
Под действием силы
F = 2i - 4j тело из точки А(2,3,-1) переместилось в точку В(1, 1, 1). Найти работу указанной силы
(1) 20
(2) 6
(3) 12
(4) 10
(5) нет верного ответа
Количество людей, посещающих магазин в выходной день увеличивается на 30% по сравнению с рабочим днем. Сколько людей посещают магазин в выходной день, если в обычный день среднее количество покупателей 600 человек?
(1) 780 человек
(2) 800 человек
(3) 790 человек
(4) 750 человек
Найти определитель матрицы по теореме о разложении определителя по элементам второго столбца. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) -18, 12, 12
(2) 18, -12, -12
(3) -18, 12, -12
(4) нет верного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить определители
(1) 27
(2) 408
(3) -192
(4) нет правильного ответа
Найти определитель матрицы по теореме о разложении определителя по элементам второго столбца. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) 24, -66, 91
(2) 15, 0, -48
(3) -30, 0, -3
(4) нет верного ответа
Если из 111 вычесть 67, то получится
(1) 34
(2) 42
(3) 44
(4) нет правильного ответа.
Вычислить детерминант
(1) -50
(2) -58
(3) 22
(4) 50
(5) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если ![math]()
х=5, то чему равен 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Вычислить детерминант
(1) 1
(2) -1
(3) 0
(4) 2
(5) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) прямая
(2) окружность
(3) спираль
(4) нет правильного ответа
На плоскости заданы две точки
А(-2,1) и В(2,-2). Чему равна длина проекции отрезка АВ на ось 0y?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 2 находится в точке с координатами
О(-2,-2). Сколько общих точек окружность имеет с координатными осями
(1) 1 точку
(2) 2 точки
(3) 3 точки
(4) 4 точки
(5) ни одной
5!-3!=?
(1) 120
(2) 114
(3) 104
(4) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если книга вдвое дороже журнала, который в 5 раз дешевле словаря, то во сколько раз словарь дороже книги?
(1) в 1,5 раза
(2) в 2,5 раза
(3) в 10 раз
(4) нет правильного ответа
Если
a>b, b>c, c>d, то тогда d
(1) больше
b
(2) самое маленькое число
(3) лежит между
c и b Даны две прямые
y+x=2 и y+3x=4. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
0,25 часа составляет
(1) 25 минут
(2) 10 минут
(3) 12 минут
(4) 15 минут
Во сколько раз 111 меньше 111 111?
(1) в 11 раз
(2) в 111 раз
(3) в 1001 раз
Выбрать самое большое число:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Минором называется
(1) определитель, который получается из основного вычеркиванием одного из столбцов
(2) определитель, получающийся из основного вычеркиванием одной строки и одного столбца
(3) определитель, который получается из основного вычеркиванием любой строки
(4) определитель, который получается из основного вычеркиванием одного из столбцов и строки того же номера
Если в квадратной матрице две строки равны, то
(1) определитель равен нулю
(2) определитель положителен
(3) определитель отрицателен
Система называется определенной, если
(1) имеет единственное решение
(2) имеет любое количество решений
(3) имеет по крайней мере два различных решения
Ведущие элементы системы называют коэффициенты
(1) стоящие на главной диагонали
(2) стоящие на главной диагонали, если система предварительно приведена к диагональному виду
(3) наибольшие коэффициенты в каждой из строк
Даны векторы
a(-7; 2) и b(14; k). Чему должно быть равно k, чтобы эти векторы были коллинеарны?
(1) 4
(2) 23
(3) 5
(4) -4
(5) ни один из предложенных
Определите, является ли числовым полем следующее множество:
... -(М+1) -М ... -101 -100 ... -4 -3 -2 -1 0 1 2 3 4 ... 100 101 ... М М+1 ...
(1) да
(2) нет
Мерность пространства определяет...
(1) количество координатных осей на каждой из которых заданы единичные векторы, обычно обозначаемые как ![math]()

(2) множество векторов на всех плоскостях и всех прямых, проходящих через начало координат
(3) количество координатных осей
(4) совокупность его элементов
Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) 2
(3) -3
(4) -14
(5) ни один из данных ответов
Элементами матрицы могут быть
(1) только числа
(2) только функции
(3) только матрицы
(4) числа, функции, матрицы
Если количество столбцов в матрице равно количеству строк, то такая матрица называется
(1) не особенной
(2) квадратной
(3) прямоугольной
Определитель
, составленный из коэффициентов при неизвестных системы называется
(1) определителем системы
(2) алгебраическим дополнением системы
(3) детерминантом матрицы
Решения ![math]() и
и ![math]() считают различными, если
считают различными, если
 и
и  считают различными, если
считают различными, если
(1) все числа ![math]() не совпадают с
не совпадают с ![math]()
 не совпадают с
не совпадают с 
(2) хотя бы одно из чисел ![math]() не совпадает с соответствующим числом
не совпадает с соответствующим числом ![math]()
 не совпадает с соответствующим числом
не совпадает с соответствующим числом 
(3) как мимнимум два числа ![math]() не совпадает с соответствующими двумя числамм
не совпадает с соответствующими двумя числамм ![math]()
 не совпадает с соответствующими двумя числамм
не совпадает с соответствующими двумя числамм 
Даны векторы
a(-2;6) и b(k;-3). Чему должно быть равно k, чтобы эти векторы были перпендикулярны?
(1) -9
(2) 9
(3) 1
(4) 0
(5) ни один из предложенных
Основное свойство умножения вектора на число записывают как
(1)
(xy)a=x(ya); xa+ya=(x+y)a
(2)
x0=0; 0a=0; |xa|=|x|·|a|
(3)
(xy)a=x(ya); xa+ya=(x+y)a; xa+xb=x(a+b) Основное свойство умножения вектора на число записывают как
(1)
(xy)a=x(ya); xa+ya=(x+y)a
(2)
x0=0; 0a=0; |xa|=|x|·|a|
(3)
(xy)a=x(ya); xa+ya=(x+y)a; xa+xb=x(a+b) Определите, является ли данное множество линейным пространством: Множество всех матриц размером
m × n
(1) да
(2) нет
Евклидовым пространством можно назвать...
(1) любое
n-мерное пространство, в котором определена базисная система линейно независимых векторов
(2) любое
n-мерное пространство, в котором определено скалярное произведение
(3) любое
n-мерное пространство, в котором базисные вектора взаимно ортогональны
(4) любое
n-мерное пространство, в котором определена длина вектора Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если в матрице два столбца равны, то
(1) вычеркивается один из них
(2) вычеркивается оба столбца
(3) определитель равен нулю
Если ![math]() , то матрицы
, то матрицы
 , то матрицы
, то матрицы А и В имеют размеры, соответственно
(1)
m×p; p×n
(2)
m×n; m×n
(3)
m×m; n×n При применении метода Крамера получилось
Δ=5; Δx=10; Δy=0;. Исходная система уравнений имеет вид
(1)
(2)
(3)
Дан вектор ![math]() . Найти координаты точки
. Найти координаты точки
 . Найти координаты точки
. Найти координаты точки В, если A(-6;-9)
(1)
B(-2;-6)
(2)
B(-2;6)
(3)
B(10;6)
(4)
B(-2;-12)
(5) ни один из предложенных
Определите какое из приведенных множеств является отображаемым по отношению к исходному (данному): автомобили
(1) техника
(2) легковые автомобили
(3) грузовые автомобили
(4) спец. техника
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если в определителе два столбца пропорциональны, то
(1) этот определитель равен нулю
(2) один из столбцов вычеркиваем
(3) пропорциональные столбцы складываем
Матрица
B=(-1)A называется
(1) обратной матрице
А
(2) симметрической матрице
А
(3) противоположной матрице
А Ответьте на вопрос: совместны ли системы уравнений?
(1) совместна
(2) не совместна
Векторными называются такие величины, которые характеризуются
(1) только направлением
(2) некоторым числовым значением
(3) не только числовым значением, но и своим направлением
Даны векторы
a(1;0;2) и b(3;4;0). Чему должно быть равно векторное произведение [a,b]?
(1)
(2)
(3)
(4) ни один из предложенных
Даны векторы
a(1;0;2) и b(3;4;0). Чему должно быть равно векторное произведение [a,b]?
(1)
(2)
(3)
(4) ни один из предложенных
Вычислить определитель
(1) 2121
(2) 2412
(3) 2514
(4) 3212
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выписать все алгебраические дополнения определителя ![math]()

(1) 1; 2; 1; 4
(2) 1; -2; -1; 4
(3) -1; -2; -1; -4
(4) 1; -1; 2; 4
Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3:
(1) 2; 3; 5
(2) 6; 20; 6
(3) 1; 2; -5
(4) нет ответа
Система однородных уравнений имеет
(1) определитель, равный нулю
(2) нулевую правую часть
(3) одно или несколько линейно зависимых уравнений
Найти угол между векторами
a(9;0;-2); b(0;15;0):
(1) 0°
(2) 45°
(3) 90°
(4) 180°
Найти скалярное произведение векторов
a = (2, 4, 1) и b = (3, 0, 8), а также косинус угла между этими векторами.
(1) 14, 0,6528
(2) 15, 0,3576
(3) 14, 0,3576
(4) 15, 0,6528
(5) нет верного ответа
Найти скалярное произведение векторов
a = (2, 4, 1) и b = (3, 0, 8), а также косинус угла между этими векторами.
(1) 14, 0,6528
(2) 15, 0,3576
(3) 14, 0,3576
(4) 15, 0,6528
(5) нет верного ответа
Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если в определителе две строки пропорциональны, то
(1) определитель равен нулю
(2) пропорциональную строку вычеркиваем
(3) определитель раскладывается на два
Определите, какой ответ является решением системы. Ответы даны в последовательности
х1; х2; х3; х4:
(1) 12,5; 1; -2,4; 3
(2) -1; 3; 0; 9
(3) 20,5; -10; -5,5; -49
(4) нет ответа
Матричный метод в решении систем линейных уравнений заключается в
(1) вычислении определителей
(2) приведение системы уравнений к треугольному виду
(3) умножении слева на обратную матрицу
Под расстоянием между точками
А и В понимают
(1) траекторию движения точки от
А к В
(2) модуль вектора ![math]()

(3) разность абсцисс указанных точек
Найти скалярное произведение векторов
a и b, заданными в координатной форме: a = 4i - 5j ; b = 3i - 2j
(1) 22
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Найти скалярное произведение векторов
a и b, заданными в координатной форме: a = 4i - 5j ; b = 3i - 2j
(1) 22
(2) 15
(3) 2
(4) 10
(5) нет верного ответа
Используя формулы Крамера, решить систему уравнений:
(1) (-2; 1; -1)
(2) (-6; 4;-3 )
(3) (-2; -3; -1)
(4) (-5; 1; -1)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если все элементы строки в определителе умножить на какое-либо число, то
(1) определитель умножится на это число
(2) так делать нельзя
(3) определитель станет равным
(mn)D, где m - число, n - количество элементов строки, D – определитель Найти определитель матрицы методом звездочки
(1) 8
(2) 12
(3) -4
(4) 1
(5) нет правильного ответа
Три вектора называются компланарными, если
(1) они лежат в одной плоскости
(2) любые два из них лежат в одной плоскости
(3) они параллельны одной плоскости
Даны векторы
a = (2,3) и b = (3, 0). Найти координаты вектора c = a - 3b
(1) (6;2)
(2) (7;3)
(3) (2;-3)
(4) (-7;3)
Даны векторы
a = (2,3) и b = (3, 0). Найти координаты вектора c = a - 3b
(1) (6;2)
(2) (7;3)
(3) (2;-3)
(4) (7;-3)
(5) нет верного ответа
Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 10; 0,5431
(2) 12; 0,7731
(3) 16; 0,6615
(4) 3; 0,3642
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Как изменится определитель, если каждый его элемент заменить элементом, симметричным с данным относительно "центра" определителя?
(1) изменит знак
(2) не изменится ничего
(3) изменит знак, если количество перестановок нечетное
(4) не изменится ничего, если количество перестановок четное
(5) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) 62
(2) 52
(3) 42
(4) 32
(5) нет правильного ответа
Даны векторы
a = (5; 12) и b = (0; 2). Найти скалярное произведение векторов (a—b)·a
(1) 145
(2) 120
(3) 160
(4) 140
(5) нет верного ответа
Даны векторы
a = (5; 12) и b = (0; 2). Найти скалярное произведение векторов (a—b)·a
(1) 145
(2) 120
(3) 160
(4) 140
(5) нет верного ответа
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) 3
(4) 1

(1) ![math]()

(2) ![math]()

(3) ![math]()

Как изменится определитель, если все его элементы заменить на обратные, т.е. на ![math]() ?
?
 ?
?
(1) тогда определители будут тоже обратными друг к другу, т.е. ![math]()

(2) это будет новый определитель, никак не связанрый с исходным, если количество строк в определителе больше 2
(3) это будет новый определитель, никак не будет связанный с исходным
(4) тогда детерминанты этих определителей будут тоже обратными друг к другу, т.е. ![math]() , если определитель второго порядка
, если определитель второго порядка
 , если определитель второго порядка
, если определитель второго порядка
(5) если это определитель второго порядка, то второй определитель можно вычислить по специальной формуле
(6) нет правильного ответа
Найти определитель матрицы методом звездочки
(1) -4
(2) -10
(3) -8
(4) -12
(5) нет правильного ответа
Даны векторы
a = (1,-1) и b = (2,-3). Найти координаты вектора c= a+2b
(1) (-5; 7)
(2) (5; 7)
(3) (5; -7)
(4) (-5; -7)
(5) нет верного ответа
Даны векторы
a = (1,-1) и b = (2,-3). Найти координаты вектора c= a+2b
(1) (-5; 7)
(2) (5; 7)
(3) (5; -7)
(4) (-5; -7)
(5) нет верного ответа
определить, являются ли вектора
а1, а2, а3 базисом и найти координаты вектора С в этом базисе. Если предложенная система окажется линейно зависимой, замените первый вектор вектором с и найдите координаты оставшегося вектора в новом базисе: а1(2,2,1), а2(4,1,1), а3(0,2,0), С(0,1,0)
(1) невозможно
(2) (7, 4, 3)
(3) (0,5, 0; -1)
(4) (-1; 2; 0)
(5) возможно
Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (9; -3; -3; 2)
(2) (2; 8; -21; 31)
(3) (-4; -45; -67; 7)
(4) (-1; 0; 3; 6)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 8 и 9
(2) 9 и 10
(3) 10 и 11
(4) 11 и 12
Как изменится определитель матрицы размера 3x3, если его "развернуть" на 90° по часовой стрелке вокруг "центра"?
(1) не изменится
(2) изменит знак
(3) определители будут взаимно обратными, т.е. ![math]()

(4) определители будут взаимно обратными, но с противоположным знаком т.е. ![math]()

Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 44, 36, 8
(2) 44, 32, 12
(3) 40, 44, -4
(4) 36, 35, 1
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,0]; B[3,2,2]; C[5,4,3], D[2,3,2]
(1) 5/6
(2) 3/4
(3) 2/3
(4) 1/2
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,0]; B[3,2,2]; C[5,4,3], D[2,3,2]
(1) 1,17
(2) 2,45
(3) 1,56
(4) -2,5
(5) нет верного ответа
Найти площадь треугольника
АВС, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 3,6
(2) 5,1
(3) 4,9
(4) 3,2
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет решения
Указать правильное значение определителя:
(1)
abcd
(2)
bcd(a-3)
(3)
cd-3ab
(4) нет ответа
Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 132, 70, 62
(2) 132, 80, 52
(3) 112, 70, 42
(4) 102, 70, 32
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если A(1; 0; 2), B(2; 1; 2), C(3;1;0)
(1) 12,5
(2) 9,56
(3) 5
(4) 3
(5) нет верного ответа
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если A(1; 0; 2), B(2; 1; 2), C(3;1;0)
(1) 12,5
(2) 9,56
(3) 5
(4) 3
(5) нет верного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,0]; B[3,2,2]; C[5,4,3], D[2,3,2]
(1) 1,234
(2) 0,764
(3) 0,871
(4) 0,543
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Указать правильное значение определителя:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти определитель матрицы методом Саррюса.
Так как при этом вычисляются две группы слагаемых, входящих в формулу с плюсом
(a11a22a33+a12a23a31+a21a13a32
и минусом (a13a22a31+a12a21a33+a11a23a32,
то для контроля за решением требуется вычислить отдельно значения этих групп, и сравнить результат в
порядке - положительные члены, отрицательные члены, результат
(1) 116, 128, -4
(2) 124, 134, -10
(3) 116, 124, -8
(4) 116, 128, -12
(5) нет верного ответа
Вычислить площадь треугольника с вершинами
A(-1;0;2); B(1;-2;5) и C(3;0;-4)
14
Вычислить площадь треугольника с вершинами
A(-1;0;2); B(1;-2;5) и C(3;0;-4)
(1) 9
(2) 8
(3) 7
(4) 14
(5) 6
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, -9
(2) да, -1
(3) нет, -4
(4) да, 8
Если ![math]() то чему равен
то чему равен ![math]() ?
?
 то чему равен
то чему равен  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Указать правильное значение определителя:
(1)
...=1
(2)
...=0
(3) ![math]()

Найти определитель матрицы по теореме о разложении определителя по элементам второй строки. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) -3, -27, -12
(2) 3, 27, 12
(3) -3, 27, -12
(4) 3, -27, 12
К телу приложена сила
F(2, 1, 2), под действием которой тело перемещается из точки А(1, 1, 1) в точку В(6, -1, 3). Найти работу, совершаемую силой по перемещению тела из точки А в точку В
(1) 20
(2) 6
(3) 12
(4) 10
(5) нет верного ответа
К телу приложена сила
F(2, 1, 2), под действием которой тело перемещается из точки А(1, 1, 1) в точку В(6, -1, 3). Найти работу, совершаемую силой по перемещению тела из точки А в точку В
(1) 20
(2) 6
(3) 12
(4) 10
(5) нет верного ответа
Раньше на полевые работы отправляли геологов на 60% больше, чем теперь. Сколько геологов отправляли раньше, если сейчас отправляют 50 человек?
(1) 70 человек
(2) 75 человек
(3) 80 человек
(4) 85 человек
Вычислить определители
(1) 66
(2) 18
(3) 28
(4) нет верного ответа
Найти определитель матрицы по теореме о разложении определителя по элементам второго столбца. В ответах приводятся только члены разложения. Члены разложения приводятся в порядке следования для первого, второго и третьего элемента столбца или строки
(1) -12, -48, -28
(2) -10, 10, 12
(3) -6, 10, 4
(4) нет верного ответа
Даны векторы
a = mi + 2j +3k, b = i + 3j -5k. При каком значении m они будут перпендикулярны?
9
Даны векторы
a = mi + 2j +3k, b = i + 3j -5k. При каком значении m они будут перпендикулярны?
(1) 9
(2) 5
(3) -9
(4) -5
(5) нет верного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()
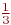
(2) ![math]()
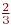
(3) ![math]()

(4) ![math]()

Вычислить определители
(1) -135
(2) 22
(3) 102
(4) нет правильного ответа
Если из 57 вычесть 38, то в остатке будет
(1) 20
(2) 18
(3) 17
(4) 19
Вычислить детерминант
(1) 2121
(2) -2121
(3) 1245
(4) нет правильного ответа
Если ![math]()
х=81, то чему равен 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить детерминант
(1) 100
(2) 50
(3) 10
(4) 1
(5) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Найти присоединенную матрицу
(1)
(2)
(3)
(4)
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) 2-х лепестковая роза
(2) прямая
(3) окружность
(4) нет правильного ответа
Заданы точки
А(17, -2) и В(3, -2). Чему равна длина отрезка АВ
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 2 находится в точке с координатами
(3,0). Сколько общих точек имеет окружность с координатными осями?
(1) ни одной
(2) 1
(3) 2
(4) 3
(5) 4
Чему равно
2!+3!?
(1) 5
(2) 6
(3) 8
(4) 10

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если на 1-ом курсе студентов в 1,5 раза больше, чем на 3-ем, и в 2,5 раза больше, чем на 4-ом, то во сколько раз на 4-ом курсе меньше студентов по сравнению с 3-им курсом?
(1) в 3/5 раза
(2) в 2 раза
(3) нет правильного ответа
(4) в 5/3 раза
Если
a>c и a<b<k, то c
(1) меньше
k
(2) больше
k
(3) равно
k Даны две прямые
2y+x=1 и y+2x=2. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
0,3 часа составляют:
(1) 18 минут
(2) 20 минут
(3) 15 минут
(4) нет правильного ответа
Во сколько раз 148 больше 37?
(1) в 4 раза
(2) в 5 раз
(3) в 4,5 раза
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Определите, является ли числовым полем следующее множество: Множество всех чисел
(1) да
(2) нет
Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 5
(2) 2
(3) -3
(4) -13
(5) ни один из данных ответов
Определите, является ли данное множество линейным пространством: Множество многочленов степени 3 с вещественными коэффициентами
(1) да
(2) нет
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определите какое из приведенных множеств является отображаемым по отношению к исходному (данному): печатающие устройства
(1) принтера
(2) сканеры
(3) графопостроители
(4) магнитофон
(5) факс
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) 70
(2) 85
(3) 68
(4) 72
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Используя формулы Крамера, решить систему уравнений:
(1) (1; 3; 7)
(2) (4; 1; -3)
(3) (2; 5; 6)
(4) (3; 2; 1)
Если ![math]() тогда
тогда
 тогда
тогда х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 25; 0,4321
(2) 12; 0,5464
(3) 23; 0,7883
(4) 13; 0,1223
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Как изменится определитель, если каждый его элемент заменить симметричным с данным относительно побочной диагонали?
(1) изменит знак
(2) не изменится ничего
(3) изменит знак, если количество перестановок нечетное
(4) не изменится ничего, если количество перестановок четное
(5) нет правильного ответа
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 0
(2) 2
(3) 9
(4) 4

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (14,5; 554; -4; 51)
(2) (20,5; -10; -5,5; -49)
(3) (11,3; 432; -4,3; 51)
(4) (12,7; 323; -3,2; 43)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 6 и 7
(2) 7 и 8
(3) 8 и 9
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,1]; B[2,3,4]; C[4,3,2]
(1) 9,9
(2) 5,6
(3) 9,8
(4) 1,3
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Указать правильное значение определителя:
(1)
bcd2
(2)
-bcd2
(3)
abcd
(4) нет ответа
Найти объем треугольной пирамиды
ABCD, если А[0,1,2], B[2,4,1], C[3,2,2], D[1,5,3]
(1) 4
(2) 3
(3) 6
(4) 2
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Указать правильное значение определителя:
(1)
=(a+b+c+d)4
(2)
=(a2+b2+c2+d2)2
(3) другой ответ
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, 5
(2) нет, 2
(3) нет, 4
(4) да, 7
При каком значении ![math]() ?
?
x верно выражение  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Количество людей, посещающих библиотеку в выходной день увеличивается на 75% по сравнению с рабочим. Сколько людей посещают библиотеку в выходной день, если в обычный день среднее количество читателей 500 человек?
(1) 800 человек
(2) 875 человек
(3) 900 человек
(4) 850 человек
Вычислить определители
(1) 260
(2) 18
(3) 248
(4) нет верного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить определители
(1) 6
(2) -6
(3) 2
(4) нет правильного ответа
Если из 123 вычесть 55, то получится
(1) 68
(2) 69
(3) 67
(4) 66
Вычислить детерминант
(1) 70
(2) 80
(3) 90
(4) нет правильного ответа
Если ![math]() , то чему равен
, то чему равен ![math]()
 , то чему равен
, то чему равен 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить детерминант
(1) 3
(2) 2
(3) 1
(4) 0
(5) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) прямая;
(2) окружность;
(3) точка;
(4) спираль.
Заданы две точки
А( 3,-6) и В(0,-5). Какова длина отрезка АВ?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 2 находится в точке с координатами
(1,1). Сколько раз окружность пересекает координатные оси?
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно
0!+4!?
(1) 25
(2) 24
(3) 12
(4) 13

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если собрали яблок в 6 раз больше, чем груш, и вдвое больше, чем слив, то во сколько раз больше собрали слив по сравнению с грушами?
(1) в 4 раза
(2) в 2 раза
(3) в 3 раза
(4) груш собрали больше, чем слив
Если
c<a и a<b<k, то c должно быть
(1) меньше
b
(2) больше
b
(3) равно
b Даны две прямые
y-2x=3 и y+3x=13. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
2/5 часа составляют
(1) 22 минуты
(2) 26 минут
(3) 24 минуты
(4) 20 минут
Во сколько раз 255 больше 15?
(1) в 15 раз
(2) в 17 раз
(3) в 19 раз
Выбрать самое маленькое число:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти производную функции ![math]() в точке
в точке
 в точке
в точке х = -1:
(1) 3
(2) 0
(3) -3
(4) -13
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) 491
(2) 358
(3) 400
(4) 502
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Используя формулы Крамера, решить систему уравнений:
(1) (2; -2; 4)
(2) (-3; -4; 3)
(3) (-2; 5; 1)
(4) (-1; 2; 3)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 13; 0,5363
(2) 31; 0,2433
(3) 10; 0,9954
(4) 14; 0,9272
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 4
(2) 5
(3) 1
(4) 0

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (7; 5; 6; -2)
(2) (-5; -6; 11; 5)
(3) (6; 5; -1; 4)
(4) (8; -9; 59; 9)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 7 и 8
(2) 8 и 9
(3) 9 и 10
(4) 10 и 11
Найти периметр треугольника, если
А[1,1,1]; B[2,3,4]; C[4,3,2] его вершины
(1) 11,12
(2) 9,32
(3) 12,33
(4) 10,31
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[5,3,2]; C[2,4,3], D[5,2,1]
(1) 4
(2) 2
(3) 3
(4) 1
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) да, 5
(2) нет, 5
(3) нет, 6
(4) нет, 8
Если ![math]() то
то ![math]() ?
?
 то
то  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
После усовершенствования комбайна, его производительность увеличилась на 45%. Сколько га обрабатывает комбайн сейчас, если до усовершенствования он обрабатывал 1000 га?
(1) 1045 га
(2) 1405 га
(3) 1400 га
(4) 1450 га
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()
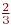
(3) ![math]()

(4) ![math]()

Вычислить определители
(1) 4,2
(2) 4,1
(3) 4,8
(4) нет правильного ответа
Если из 292 вычесть 77, то получится
(1) 211
(2) 213
(3) 215
(4) 217
Вычислить детерминант
(1) 70
(2) 60
(3) 50
(4) нет правильного ответа
Если ![math]()
х=3, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Вычислить детерминант
(1) -40
(2) -20
(3) 0
(4) 20
(5) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) точка
(2) прямая
(3) луч
(4) нет правильного ответа
Заданы две точки
А(8,-1) и В(-1, 4). Расстояние между проекциями этих точек на ось 0х равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 5 находится в точке с координатами
(7,10). Сколько раз окружность пересекает координатные оси?
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно ![math]() ?
?
 ?
?
(1) 3/2
(2) 2
(3) 15
(4) 30

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если один рабочий сделал деталей в 1,5 раза больше, чем второй, который сделал деталей в 3 раза меньше, чем третий рабочий, то первый рабочий сделал деталей по сравнению с третьим
(1) в 2 раза меньше
(2) столько же
(3) в 2 раза больше
(4) нет правильного ответа
Если
b<k и c<a<b, то k лежит
(1) левее
c
(2) между
a и b
(3) правее
c Даны две прямые
5y-3x=1 и 15y-9х=6. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
3/4 часа составляют
(1) 40 минут
(2) 50 минут
(3) 42 минуты
(4) 45 минут
Во сколько раз 23 меньше 138?
(1) в 4 раза
(2) в 8 раз
(3) в 6 раз
Выбрать наименьший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) 2
(3) -14
(4) -13
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Используя формулы Крамера, решить систему уравнений:
(1) (0; 2; 3)
(2) (0; 1; 3)
(3) (4; 3; 1)
(4) (0; 3; 1)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 11; 0,1435
(2) 12; 0,5855
(3) 21; 0,4405
(4) 17; 0,4589
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет корней
Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 0,54
(2) 0,76
(3) 0,67
(4) 0,43

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (-31; 3; 4; 5)
(2) (41; 3; -5; 6)
(3) (4; 2; 0; 5)
(4) (8; -7; 0; 31)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 11 и 12
(2) 12 и 13
(3) 10 и 11
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[1,0,1]; C[2,-1,-1]
(1) 3,21
(2) 6,3
(3) 1,73
(4) 1,45
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти объем треугольной пирамиды
ABCD, если А[1,2,0]; B[3,6,2]; C[4,5,1], D[2,5,2]
(1) 7,33
(2) 8,13
(3) 6,43
(4) 5,19
Если ![math]() , то
, то ![math]()
 , то
, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) да, 1
(2) нет, 6
(3) нет, 5
(4) да, 9
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Цена на стиральную машину увеличилась с 5000 руб. до 7000 руб. На сколько процентов увеличилась цена?
(1) на 40%
(2) на 45%
(3) на 30%
(4) на 35%
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если из 85 вычесть 19, то в остатке будет
(1) 64
(2) 66
(3) 68
(4) 70
Если ![math]()
х=256, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) прямая
(2) луч
(3) окружность
(4) спираль
Заданы две точки
А(-7,2) и В(3,4). Длина проекции отрезка АВ на прямую y=0 равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
Центр окружности радиуса 4 находится в точке с координатами
(4,5). Сколько общих точек имеет окружность с координатными осями?
(1) ни одной
(2) одну
(3) 2 точки
(4) 3 точки
(5) 4 точки
Чему равно ![math]() ?
?
 ?
?
(1) 0
(2) 6
(3) 3
(4) 2
Упростите выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если отец старше сына в 5 раз и младше дедушки втрое, то дедушка старше внука в
(1) 3/5 раза
(2) 5/3 раза
(3) 15 раз
(4) нет правильного ответа
Если
c<a и a<b и b<k, то c лежит
(1) правее всех точек
(2) между
a и b
(3) левее всех точек
Даны две прямые
3y+x=4 и y-3x=6. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
1/6 часа составляют
(1) 10 минут
(2) 20 минут
(3) 12 минут
(4) 15 минут
Во сколько раз 52 меньше 260?
(1) в 5 раз
(2) в 6 раз
(3) нет правильного ответа
Вычислить определитель
(1) -1022
(2) 2422
(3) -1126
(4) 2130
Выбрать самое большое число:
(1) ![math]()

(2) ![math]()
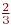
(3) ![math]()

(4) ![math]()

Найти производную функции ![math]() в точке
в точке
 в точке
в точке х = -1:
(1) 3
(2) 2;
(3) -3
(4) -15
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) 131
(2) 250
(3) 231
(4) 145
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Используя формулы Крамера, решить систему уравнений:
(1) (4; 1; -2)
(2) (0; -3; -2)
(3) (5; -5; -2)
(4) (-1; 3; -5)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 14; 0,7435
(2) 14; 0,7528
(3) 17; 0,7435
(4) 17; 0,7528
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 6,3
(2) 4,2
(3) 8,1
(4) 7,5

(1) ![math]()

(2) ![math]()

(3) ![math]()

Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 5 и 6
(2) 6 и 7
(3) 7 и 8
(4) 8 и 9
Найти площадь треугольника, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,1,2]; B[1,0,1]; C[2,-1,-1]
(1) 0,87
(2) 0,97
(3) 0,43
(4) 0,32
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти объем треугольной пирамиды
ABCD, если А[1,0,1]; B[2,2,3]; C[3,2,4], D[5,2,3]
(1) 6
(2) 4
(3) 1
(4) 9
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, -3
(2) нет, 7
(3) да, 0
(4) нет, -2
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет решения
На одной шахте добывают 115 т. угля, а на другой шахте за это же время добывают угля на 20% больше. Сколько тонн угля добывают на второй шахте?
(1) 130 т
(2) 135 т
(3) 138 т
(4) 140 т
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если из 40 вычесть 23, то получится
(1) 17
(2) 18
(3) 16
(4) 19
Если ![math]() , то
, то ![math]()
 , то
, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) 4-х лепестковая роза
(2) окружность
(3) 2-х лепестковая роза
(4) спираль
Заданы две точки
А(12,11) и В(7,-3). Длина проекции отрезка АВ на прямую х=1 равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 1 находится в точке с координатами
(1/2 ; 2). Сколько раз окружность пересекает координатные оси?
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно ![math]() ?
?
 ?
?
(1) 5
(2) 20
(3) 120
(4) 60

(1) ![math]()

(2) нет правильного ответа
(3) ![math]()

Если
c<a<b и b<k, то a должно быть
(1) меньше
k
(2) больше
k
(3) равно
k Даны две прямые
y-x=1 и 2y+x=3. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
0,7 часа составляют
(1) 40 минут
(2) 42 минуты
(3) 49 минут
(4) нет правильного ответа
Во сколько раз 999 меньше 999 999?
(1) в 111 раз
(2) в 1001 раз
(3) в 11 раз
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3;
(2) 2
(3) -3
(4) -4
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2)
(3) ![math]()

(4) нет правильного ответа
Используя формулы Крамера, решить систему уравнений:
(1) (3; -2; 1)
(2) (1; 2; -5)
(3) (4; 7; -3)
(4) (-2; -1; 5)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 34; 0,7484
(2) 19; 0,7654
(3) 16; 0,8956
(4) 20; 0,8377
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 5
(2) 1
(3) 8
(4) 2

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 7 и 8
(2) 8 и 9
(3) 6 и 7
Найти периметр треугольника, если
А[1,1,2]; B[1,0,1]; C[2,-1,-1] его вершины
(1) 8,43
(2) 5,21
(3) 7,61
(4) 9,12
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[4,4,3]; C[5,5,2], D[6,1,1]
(1) 5,12
(2) 6,11
(3) 4,17
(4) 3,16
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) нет решения
(4) ![math]()

Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, -4
(2) да, 0
(3) нет, -19
(4) да, 8
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Один рабочий делает за смену 52 детали, а другой на 25% больше. Сколько деталей делает за смену второй рабочий?
(1) 60 деталей
(2) 65 деталей
(3) 63 детали
(4) 64 детали
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если из 333 вычесть 155, то получится
(1) 172
(2) 174
(3) 176
(4) 178
Если ![math]()
х=125, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) спираль
(2) з-х лепестковая роза
(3) 6-ти лепестковая роза
(4) окружность
Заданы две точки
А(0,7) и В(-9, 2). Длина проекции отрезка АВ на прямую y=3 равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 1 находится в точке с координатами
( -1/2 ; 1). Сколько общих точек имеет окружность с координатными осями?
(1) ни одной
(2) одну
(3) 2 точки
(4) 3 точки
(5) 4 точки
Чему равно
(2!-3!)?
(1) -4
(2) -6
(3) 4
(4) 6
Чему равно выражение ![math]() ?
?
 ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если в классе "отличников" втрое меньше, чем "троечников", а "двоечников" меньше, чем "троечников", в 4 раза, то "отличников" больше, чем "двоечников" в
(1) 7 раз
(2) 12 раз
(3) ![math]() раз
раз
 раз
раз
(4) "отличников" меньше, чем "двоечников"
Если
c<a<k и a<b<k, то k
(1) самое большое число
(2) лежит между
c и b
(3) лежит левее
b Даны две прямые
y+5x=1 и 9y+45x=0. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом
0,8 часа составляют
(1) 46 минут
(2) 44 минуты
(3) 45 минут
(4) 48 минут
Во сколько раз 630 больше 21?
(1) в 15 раз
(2) в 25 раз
(3) в 30 раз
Вычислить определитель
(1) 12
(2) 14
(3) 8
(4) 10
Выбрать самое большое число:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) 11
(3) -3
(4) -13
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) 1
(2) 3
(3) 5
(4) 7
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Используя формулы Крамера, решить систему уравнений:
(1) (1; -3; 4)
(2) (2; -2; 3)
(3) (-3; -2; 4)
(4) (2; 3; 1)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 13; 0,9432
(2) 22; 0.5464
(3) 21; 0,9105
(4) 19; 0,5463
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 3
(2) -2
(3) -1
(4) 4

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (4,1; 2,2; 3,1; 4,2)
(2) (1,3; 2,1; -4,1; -3,1)
(3) (1,4; -0,1; -0,4; 0,7)
(4) (2,1; 3,2; -4,1; 0)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 5 и 6
(2) 3 и 4
(3) 6 и 7
(4) 4 и 5
Найти площадь параллелограмма, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,0,2]; B[1,5,3]; C[2,2,0]
(1) 18,34
(2) 14,36
(3) 17,75
(4) 7,32
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) нет решения
(4) нет правильного ответа
Найти объем треугольной пирамиды
ABCD, если А[0,1,0]; B[2,3,2]; C[3,2,3], D[5,5,4]
(1) 0,43
(2) 0,12
(3) 0,67
(4) 0,54
Если ![math]() то
то
 то
то x=?
(1) -1 или 3
(2) 1 или -1
(3) нет правильного ответа
(4) 1
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) да, 6
(2) нет, 7
(3) да, 0
(4) нет, 1
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
В магазине действует предпраздничная скидка 20%. Во сколько обойдется покупка школьных принадлежностей, если обычно на них уходит 150 руб.?
(1) 120 рублей
(2) 130 рублей
(3) 110 рублей
(4) 125 рублей
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
Если из 246 вычесть 98, то результат будет равен
(1) 146
(2) 148
(3) 152
(4) 154
Если ![math]()
х=2, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если линия задана уравнением ![math]() , то это
, то это
 , то это
, то это
(1) окружность
(2) 2 полуокружности
(3) спираль
(4) прямая
Заданы две точки
А(3,-1) и В(0,-8). Расстояние между проекциями этих точек на прямую х=5 равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 2,5 находится в точке с координатами ![math]() . Сколько раз окружность пересекает координатные оси?
. Сколько раз окружность пересекает координатные оси?
 . Сколько раз окружность пересекает координатные оси?
. Сколько раз окружность пересекает координатные оси?
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно ![math]() ?
?
 ?
?
(1) 20
(2) 24
(3) 120
(4) 720
 ?
?
(1) нет правильного ответа
(2) ![math]()

(3) ![math]()

(4) ![math]()

Если 1 кг винограда вдвое дороже, чем 1 кг мандарин, и в 8 раз дороже, чем 1 кг арбузов, то 1 кг арбузов дешевле, чем 1 кг мандарин в
(1) 4 раза
(2) 16 раз
(3) 6 раз
(4) нет правильного ответа
Если
m<n, p<s и p>n, то p должно быть
(1) больше
m
(2) меньше
m
(3) равно
m Даны две прямые
7y-х=8 и y+7x=3. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом, отличным от 90°
0,1 часа составляет
(1) 10 минут
(2) 8 минут
(3) 6 минут
(4) 4 минуты
Во сколько раз 27 меньше 729?
(1) в 27 раз
(2) в 17 раз
(3) в 24 раза
Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 3
(2) -12
(3) -3
(4) -13
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) -3
(2) -5
(3) -6
(4) -1
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Используя формулы Крамера, решить систему уравнений:
(1) (9; 1; 4)
(2) (8; 4; 2)
(3) (6; 7; 8)
(4) (1; 3; 0)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 16; 0,9562
(2) 17; 0,3904
(3) 29; 0,4563
(4) 15; 0,4563
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 4,2
(2) 6.2
(3) 3,4
(4) 4,5

(1) ![math]()

(2) ![math]()

(3) ![math]()

Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (68; -31; -43; -8)
(2) (-45; -34; 6; 24)
(3) (112; 4; -10; 7)
(4) (-103; -24; -9; 8)
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 7 и 8
(2) 8 и 9
(3) 9 и 10
Найти площадь треугольника, построенного на векторах ![math]() и
и ![math]() , если
, если
 и
и  , если
, если А[1,0,2]; B[1,5,3]; C[2,2,0]
(1) 9,65
(2) 6,32
(3) 8,87
(4) 3,56
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Найти объем треугольной пирамиды
ABCD, если А[1,1,1]; B[5,0,2]; C[4,0,4], D[0,6,4]
(1) 5,54
(2) 8,03
(3) 7,67
(4) 4,32
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) нет, 6
(2) да, 3
(3) да, 0
(4) нет, -3
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
В стоимость билета на футбольный матч входит цена футболки, которая составляет 75 руб. Сколько процентов составляет цена футболки относительно цены всего билета, если билет стоит 300 рублей?
(1) 20%
(2) 30%
(3) 25%
(4) 35%
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) нет правильного ответа;
(4) ![math]()

Если из 139 вычесть 81, то получится
(1) 48
(2) 56
(3) 58
(4) нет правильного ответа.
Если ![math]()
х=71, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Заданы две точки
А(-2, -1) и В(-2, 15). Длина отрезка АВ равна
(1) 16
(2) 0
(3) 14
(4) 10
Центр окружности радиуса 3,5 находится в точке с координатами
(4, 1/4). Сколько общих точек имеет окружность с координатными осями?
(1) ни одной
(2) одну
(3) 2 точки
(4) 3 точки
(5) 4 точки
Чему равно ![math]() ?
?
 ?
?
(1) 1/5
(2) 1/20
(3) 6/5
(4) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если
m<n, p<s и p>n, то n лежит
(1) между
p и s
(2) между
m и s
(3) правее
p Даны две прямые
6y-2х=10 и 3y-х=0. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом, отличным от 90°
1/12 часа составляет
(1) 3 минуты
(2) 5 минут
(3) 4 минуты
(4) 6 минут
Во сколько раз 39 больше 13?
(1) в 4 раза
(2) в 3 раза
(3) в 2 раза
Выбрать самое большое число:
(1) ![math]()
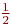
(2) ![math]()
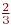
(3) ![math]()

(4) ![math]()

Найти производную функции ![math]()
f(x) в точке х = -1: 
(1) 13
(2) 2
(3) -13
(4) -29
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить определитель
(1) 16
(2) -25
(3) -20
(4) 32
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти матрицу, обратную данной
(1)
(2)
(3)
(4)
Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Используя формулы Крамера, решить систему уравнений:
(1) (4; 5; 9)
(2) (1; 0; 5)
(3) (3; 2; 4)
(4) (2; 3; 5)
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти скалярное произведение векторов ![math]() и
и ![math]() , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
 и
и  , а также косинус угла между этими векторами
, а также косинус угла между этими векторами
(1) 4; 0,5644
(2) 24; 0,4955
(3) 28; 0,6657
(4) 34; 0,4537
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны векторы ![math]() . При каком значении
. При каком значении
 . При каком значении
. При каком значении m они будут перпендикулярны?
(1) 6
(2) 2
(3) 9
(4) 1
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 7 и 8
(2) 8 и 9
(3) 6 и 7
Найти периметр треугольника, если
А[1,0,2]; B[1,5,3]; C[2,2,0] его вершины
(1) 14,56
(2) 13,35
(3) 12,46
(4) 16,21
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) нет решения
(4) ![math]()

Найти объем треугольной пирамиды ABCD, если
А[1,1,1]; B[4,3,3]; C[4,5,4], D[5,5,6]
(1) 2,34
(2) 5,52
(3) 1,67
(4) 0,98
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет решения
Принадлежат ли одной плоскости векторы, если ![math]() ? Чему равно значение определителя?
? Чему равно значение определителя?
 ? Чему равно значение определителя?
? Чему равно значение определителя?
(1) да, 3
(2) нет, 11
(3) да, 31
(4) нет, -21
Какова масса соли в 3% -ном растворе, если масса всего раствора составляет 200 г ?
(1) 10 г
(2) 5 г
(3) 3 г
(4) 6 г
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если из 72 вычесть 35, то получится
(1) 37
(2) 38
(3) 36
(4) нет правильного ответа
Если ![math]() , то
, то ![math]()
 , то
, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа.
Заданы две точки ![math]() и
и
 и
и В(2,0). Длина отрезка АВ рана
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 1,5 находится в точке с координатами ![math]() . Сколько раз окружность пересекает координатные оси?
. Сколько раз окружность пересекает координатные оси?
 . Сколько раз окружность пересекает координатные оси?
. Сколько раз окружность пересекает координатные оси?
(1) ни разу
(2) 1 раз
(3) 2 раза
(4) 3 раза
(5) 4 раза
Чему равно
4!-2!?
(1) 2
(2) 20
(3) 22
(4) 10

(1) ![math]()

(2) ![math]()

(3) ![math]()

Если в тексте буква "а" встречается в 10 раз чаще, чем буква "р", которая встречается чаще, чем буква "т" в 5 раз, то буква "а" встречается чаще, чем буква "т" в
(1) 5 раз
(2) 50 раз
(3) 15 раз
(4) 2 раза
Даны две прямые
y+4x=7 и 2y-x=5. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом, отличным от 90°
1/15 часа составляет
(1) 4 минуты
(2) 3 минуты
(3) 6 минут
(4) 8 минут
Во сколько раз 55 больше 25 ?
(1) в 2,5 раза;
(2) в 2 раза
(3) в ![math]() раза
раза
 раза
раза Применяя метод исключения неизвестных (Гаусса), решить систему линейных уравнений:
(1) (-7; 6; 5; -4)
(2) (7; -5; -1; 1)
(3) (1; 3; 0; -7)
(4) (-6; 5; -3; 1)
Выбрать самое маленькое число:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти производную функции ![math]() в точке
в точке
 в точке
в точке х = -1:
(1) 3
(2) 0
(3) -3
(4) -13
(5) ни один из данных ответов
Преобразовать выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Выбрать наибольший результат
(1) ![math]()

(2) ![math]()

(3) ![math]()

Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Упростить выражение ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если ![math]() то
то
 то
то х=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()


(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Значение ![math]() заключено между
заключено между
 заключено между
заключено между
(1) 6 и 7
(2) 9 и 10
(3) 7 и 8
(4) 8 и 9
Если ![math]() , то
, то
 , то
, то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) 2 и 9
Если ![math]() то
то
 то
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Имеется 5 кг сплава железа и серебра. Сколько кг серебра содержится в сплаве, если его доля составляет 40% ?
(1) 2 кг
(2) 3 кг
(3) 1,5 кг
(4) 2,5 кг
Если ![math]() то x=?
то x=?
 то x=?
то x=?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если из 222 вычесть 196, то получится
(1) 24
(2) 26
(3) нет правильного ответа
(4) 28
Если ![math]()
х=121, то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Заданы две точки ![math]() и
и
 и
и В(0,1). Длина отрезка АВ равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Центр окружности радиуса 2,3 находится в точке с координатами ![math]() . Сколько общих точек имеет окружность с координатными осями?
. Сколько общих точек имеет окружность с координатными осями?
 . Сколько общих точек имеет окружность с координатными осями?
. Сколько общих точек имеет окружность с координатными осями?
(1) ни одной
(2) одну
(3) 2 точки
(4) 3 точки
(5) 4 точки
Чему равно
6!?
(1) 720
(2) 120
(3) 30
(4) 90
 = ?
= ?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) нет правильного ответа
Если в столовой стульев в 6 раз больше, чем столов, а подносов вдвое больше, чем столов, то стульев больше, чем подносов в
(1) 8 раз
(2) 3 раза
(3) 4 раза
(4) 12 раз
Если
c<a<d и d<b<f, то f
(1) самое большее число
(2) меньше
c
(3) нет правильного ответа
Даны две прямые
4y+3x=5 и 3y-4х=2. Эти прямые
(1) параллельные
(2) перпендикулярны
(3) пересекаются под некоторым углом, отличным от 90°
1/30 часа составляет
(1) 3 минуты
(2) 4 минуты
(3) 1 минуту
(4) 2 минуты
Во сколько раз 22 меньше 726?
(1) в 32 раза
(2) в 33 раза
(3) в 23 раза