Главная /
Математика /
Математический анализ - 1
Математический анализ - 1 - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс знакомит с числовыми множествами, последовательностями и функциями.
Все ответы: Курс знакомит с числовыми множествами, последовательностями и функциями.
Пусть ![math]() - множество простых чисел и
- множество простых чисел и ![math]() - натуральных. Какая из записей верна:
- натуральных. Какая из записей верна:
 - множество простых чисел и
- множество простых чисел и  - натуральных. Какая из записей верна:
- натуральных. Какая из записей верна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Указать область определения функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() называется бесконечно малой функцией при
называется бесконечно малой функцией при ![math]() , стремящемся к
, стремящемся к ![math]() , если
, если ![math]() равен
равен
 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если  равен
равен
(1) ![math]()

(2) 0
(3) ![math]()

(4) не существует
По определению, функция ![math]() называется непрерывной в точке
называется непрерывной в точке ![math]() , если
, если
 называется непрерывной в точке
называется непрерывной в точке  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

Функция ![math]() непрерывна в точке
непрерывна в точке ![math]() , если односторонние пределы в этой точке
, если односторонние пределы в этой точке
 непрерывна в точке
непрерывна в точке  , если односторонние пределы в этой точке
, если односторонние пределы в этой точке
(1) равны
(2) равны ![math]()

(3) равны бесконечности
Функция называется равномерно непрерывной на интервале ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

8
Вычислить![math]()

5
Вычислить![math]()

1
Если общий член последовательности ![math]() определяется формулой
определяется формулой ![math]() , то
, то ![math]() равен
равен
 определяется формулой
определяется формулой  , то
, то  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

1/2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
.![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
. ,
,  ,
, 
1/2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
.![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
. ,
,  ,
, 
2
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Производной функции ![math]() в данной точке
в данной точке ![math]() называется
называется
 в данной точке
в данной точке  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие равенства верны:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() , где
, где ![math]()
 , где
, где 
Функции ![math]() называются взаимно обратными, если
называются взаимно обратными, если
 называются взаимно обратными, если
называются взаимно обратными, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется ограниченной сверху, если
называется ограниченной сверху, если ![math]()
 называется ограниченной сверху, если
называется ограниченной сверху, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() есть
есть
 -го порядка
-го порядка  функции
функции  есть
есть
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
5
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Каким условиям должна удовлетворять функция ![math]() в теореме Ролля:
в теореме Ролля:
 в теореме Ролля:
в теореме Ролля:
(1) непрерывность на ![math]()

(2) непрерывность на ![math]()

(3) ограниченность на ![math]()

(4) монотонность на ![math]()

(5) дифференцируемость на ![math]()

(6) дифференцируемость в точке ![math]()

(7) ![math]()

(8) ![math]()

Какую неопределённость нужно раскрыть при вычислении предела функции ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое выражение является формулой Тейлора для многочлена степени ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
4/3
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-9
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-2
Функция ![math]() называется неубывающей на [a,b], если
называется неубывающей на [a,b], если ![math]()
 называется неубывающей на [a,b], если
называется неубывающей на [a,b], если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Наибольшее значение функция ![math]() может принимать
может принимать
 может принимать
может принимать
(1) только на концах отрезка
(2) только в точках локального максимума
(3) на концах отрезка или в точках локального максимума
(4) на концах отрезка и в точках локального максимума
Прямая ![math]() является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции ![math]() только в том случае, если
только в том случае, если
 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  только в том случае, если
только в том случае, если
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() или
или ![math]()
 или
или 
(3) ![math]() или
или ![math]()
 или
или 
(4) ![math]() и
и ![math]()
 и
и 
(5) ![math]() или
или ![math]()
 или
или 
Пусть для функции ![math]() в окрестности точки
в окрестности точки ![math]() существует производная
существует производная ![math]() -го порядка, непрерывная в
-го порядка, непрерывная в ![math]() и
и ![math]() - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда ![math]() - точка максимума
- точка максимума ![math]() , если
, если
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка, непрерывная в
-го порядка, непрерывная в  и
и  - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка максимума
- точка максимума  , если
, если
(1) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(2) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(3) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
(4) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
С помощью производной найти значение выражения ![math]() .
.
 .
.
0.5
С помощью производной найти значение выражения ![math]() .
.
 .
.
0.5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
2/11
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
-4
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
-29
Укажите область определения функции ![math]()

(1) R
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
3/5
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
1/72
Пусть ![math]() . Какое из перечисленных множеств есть множество
. Какое из перечисленных множеств есть множество ![math]() :
:
 . Какое из перечисленных множеств есть множество
. Какое из перечисленных множеств есть множество  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению (Коши), ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая из перечисленных функций является б.м.ф. при ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие из перечисленных функций непрерывны в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Точка ![math]() называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции ![math]() , если в этой точке
, если в этой точке ![math]()
 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  , если в этой точке
, если в этой точке 
(1) конечные пределы слева и справа равны
(2) конечные пределы слева и справа не равны
(3) конечный предел слева или справа не существует
 называется б.м. более высокого порядка, чем
называется б.м. более высокого порядка, чем  при
при  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

1/2
Вычислить![math]()

3/4
Вычислить![math]() .
.
 .
.
1
Число ![math]() называется пределом последовательности
называется пределом последовательности ![math]() , если
, если
 называется пределом последовательности
называется пределом последовательности  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/8
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
4
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Производной функции ![math]() является функция
является функция
 является функция
является функция
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какому условию должны удовлетворять функции ![math]() , чтобы их сумма
, чтобы их сумма ![math]() была дифференцируемой:
была дифференцируемой:
 , чтобы их сумма
, чтобы их сумма  была дифференцируемой:
была дифференцируемой:
(1) ![math]() непрерывна и
непрерывна и ![math]() дифференцируема
дифференцируема
 непрерывна и
непрерывна и  дифференцируема
дифференцируема
(2) ![math]() дифференцируема и
дифференцируема и ![math]() дифференцируема
дифференцируема
 дифференцируема и
дифференцируема и  дифференцируема
дифференцируема
(3) ![math]() дифференцируема или
дифференцируема или ![math]() дифференцируема
дифференцируема
 дифференцируема или
дифференцируема или  дифференцируема
дифференцируема Каким условием должна удовлетворять функция ![math]() для того, чтобы существовала непрерывная возрастающая обратная функция
для того, чтобы существовала непрерывная возрастающая обратная функция ![math]() :
:
 для того, чтобы существовала непрерывная возрастающая обратная функция
для того, чтобы существовала непрерывная возрастающая обратная функция  :
:
(1) непрерывность и убывание на отрезке
(2) ограниченность и возрастание на отрезке
(3) непрерывность и возрастание на отрезке
(4) ограниченность и убывание на отрезке
Последовательность ![math]() , где
, где ![math]() является
является
 , где
, где  является
является
(1) неограниченной снизу
(2) ограниченной
(3) неограниченной
Может ли существовать вторая производная ![math]() в точке
в точке ![math]() , если в неё не существует первая производная
, если в неё не существует первая производная ![math]() :
:
 в точке
в точке  , если в неё не существует первая производная
, если в неё не существует первая производная  :
:
(1) да
(2) нет
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
8
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Ролля точка ![math]()

(1) совпадает с концами отрезка ![math]() или
или ![math]()
 или
или 
(2) лежит вне отрезка ![math]()

(3) принадлежит интервалу ![math]()

Пусть ![math]() и
и ![math]() - бесконечно малые в точке
- бесконечно малые в точке ![math]() функции, для которых существует предел
функции, для которых существует предел ![math]() . Тогда существует предел
. Тогда существует предел
 и
и  - бесконечно малые в точке
- бесконечно малые в точке  функции, для которых существует предел
функции, для которых существует предел  . Тогда существует предел
. Тогда существует предел
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие условия для функции ![math]() должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки
должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки ![math]() :
:
 должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки
должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки  :
:
(1) ![math]() раз дифференцируема в окрестности точки
раз дифференцируема в окрестности точки ![math]()
 раз дифференцируема в окрестности точки
раз дифференцируема в окрестности точки 
(2) бесконечно дифференцируема в окрестности точки ![math]()

(3) дифференцируема в окрестности точки ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 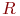 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Пусть функция ![math]() непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную ![math]() на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
 непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
(1) ![math]() на
на ![math]() неубывающая на [a,b]
неубывающая на [a,b]
 на
на  неубывающая на [a,b]
неубывающая на [a,b]
(2) ![math]() на
на ![math]() неубывающая на [a,b]
неубывающая на [a,b]
 на
на  неубывающая на [a,b]
неубывающая на [a,b]
(3) ![math]() неубывающая на
неубывающая на ![math]() на
на ![math]()
 неубывающая на
неубывающая на  на
на 
(4) ![math]() неубывающая на
неубывающая на ![math]() на
на ![math]()
 неубывающая на
неубывающая на  на
на 
График дифференцируемой на интервале ![math]() функции
функции ![math]() не имеет на этом интервале выпуклость, направленную вверх, если график
не имеет на этом интервале выпуклость, направленную вверх, если график ![math]() лежит в пределах интервала
лежит в пределах интервала
 функции
функции  не имеет на этом интервале выпуклость, направленную вверх, если график
не имеет на этом интервале выпуклость, направленную вверх, если график  лежит в пределах интервала
лежит в пределах интервала
(1) не выше любой своей касательной
(2) не ниже любой своей касательной
(3) не выше и не ниже любой своей касательной
Пусть точка ![math]() - точка разрыва функции
- точка разрыва функции ![math]() и прямая
и прямая ![math]() - вертикальная асимптота. Тогда
- вертикальная асимптота. Тогда ![math]() -
-
 - точка разрыва функции
- точка разрыва функции  и прямая
и прямая  - вертикальная асимптота. Тогда
- вертикальная асимптота. Тогда  -
-
(1) точка устранимого разрыва
(2) точка разрыва первого рода
(3) точка разрыва второго рода
Для функции ![math]() точка (0,0) графика функции является
точка (0,0) графика функции является
 точка (0,0) графика функции является
точка (0,0) графика функции является
(1) точкой максимума
(2) точкой минимума
(3) точкой перегиба
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

(5) функция убывает на ![math]()

(6) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 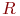 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-2
Найти наименьшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
8
Укажите область определения функции![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) R
Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть ![math]() и
и ![math]() . Какое множество является пересечением
. Какое множество является пересечением ![math]()
 и
и  . Какое множество является пересечением
. Какое множество является пересечением 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() и
и ![math]() , то
, то
 и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() или
или ![math]()
 или
или 
Если ![math]() - бесконечно малые функции при
- бесконечно малые функции при ![math]() , то
, то ![math]()
 - бесконечно малые функции при
- бесконечно малые функции при  , то
, то 
(1) равен нулю
(2) больше нуля
(3) меньше нуля
(4) не равен нулю
(5) не существует
Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() и
и ![math]() ,то
,то
 непрерывна в точке
непрерывна в точке  и
и  ,то
,то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Точка ![math]() для функции
для функции ![math]() является точкой разрыва
является точкой разрыва
 для функции
для функции  является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть ![math]() б.м.ф. при
б.м.ф. при ![math]() и
и ![math]() . Тогда
. Тогда
 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

3
Вычислить![math]()

3/8
Вычислить![math]() .
.
 .
.
1
Последовательность называется сходящейся, если её предел
(1) не существует
(2) равен конечному числу
(3) равен бесконечности
Вычислить![math]()

1/7
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
4
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
0
Угловой коэффициент какой прямой, проведённой в точке с абсциссой ![math]() , равен производной
, равен производной ![math]() функции
функции ![math]() :
:
 , равен производной
, равен производной  функции
функции  :
:
(1) касательная
(2) нормаль
(3) секущая
Производная ![math]() обратной функции
обратной функции ![math]() для функции
для функции ![math]() равна :
равна :
 обратной функции
обратной функции  для функции
для функции  равна :
равна :
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению, последовательность ![math]() называется бесконечно большой (
называется бесконечно большой (![math]() ) , если
) , если ![math]()
 называется бесконечно большой (
называется бесконечно большой ( ) , если
) , если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна ![math]() -я производная функции
-я производная функции ![math]()
 -я производная функции
-я производная функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
-5
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
-2
Дано уравнение ![math]() , точка
, точка ![math]() и уравнение прямой
и уравнение прямой ![math]() . Составить уравнение касательной к кривой в точке
. Составить уравнение касательной к кривой в точке ![math]()
 , точка
, точка  и уравнение прямой
и уравнение прямой  . Составить уравнение касательной к кривой в точке
. Составить уравнение касательной к кривой в точке 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти сумму абсцисс точек, в которых касательная к кривой ![math]() параллельна биссектрисе второго координатного угла
параллельна биссектрисе второго координатного угла
 параллельна биссектрисе второго координатного угла
параллельна биссектрисе второго координатного угла
3
Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Ролля точка ![math]()

(1) единственная
(2) хотя бы одна
Каким условиям в точке ![math]() должны удовлетворять функции
должны удовлетворять функции ![math]() и
и ![math]() , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
 должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
(1) ![math]() - бесконечно малая и -
- бесконечно малая и - ![math]() бесконечно малая
бесконечно малая
 - бесконечно малая и -
- бесконечно малая и -  бесконечно малая
бесконечно малая
(2) ![math]() - бесконечно большая и -
- бесконечно большая и - ![math]() бесконечно малая
бесконечно малая
 - бесконечно большая и -
- бесконечно большая и -  бесконечно малая
бесконечно малая
(3) ![math]() - бесконечно малая и -
- бесконечно малая и - ![math]() бесконечно большая
бесконечно большая
 - бесконечно малая и -
- бесконечно малая и -  бесконечно большая
бесконечно большая
(4) ![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]()
 и
и  непрерывны в точке
непрерывны в точке 
(5) ![math]() и
и ![math]() дифференцируемы в окрестности точки
дифференцируемы в окрестности точки ![math]()
 и
и  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 
(6) существует ![math]()

(7) существует ![math]()

Верно ли, что функция ![math]() раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки ![math]()
 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 
(1) да
(2) нет
Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-1/2
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-4
Пусть функция ![math]() непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную ![math]() на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
 непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
(1) ![math]() на
на ![math]() убывает на [a,b]
убывает на [a,b]
 на
на  убывает на [a,b]
убывает на [a,b]
(2) ![math]() на
на ![math]() убывает на [a,b]
убывает на [a,b]
 на
на  убывает на [a,b]
убывает на [a,b]
(3) ![math]() убывает на
убывает на ![math]() на
на ![math]()
 убывает на
убывает на  на
на 
(4) ![math]() убывает на
убывает на ![math]() на
на ![math]()
 убывает на
убывает на  на
на 
Какие утверждения справедливы:
(1) любая ![math]() , непрерывная на множестве
, непрерывная на множестве ![math]() , выпукла вверх или вниз на некотором интервале
, выпукла вверх или вниз на некотором интервале ![math]()
 , непрерывная на множестве
, непрерывная на множестве 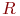 , выпукла вверх или вниз на некотором интервале
, выпукла вверх или вниз на некотором интервале 
(2) любая ![math]() , дифференцируемая на интервале
, дифференцируемая на интервале ![math]() , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале
 , дифференцируемая на интервале
, дифференцируемая на интервале  , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале
(3) любая ![math]() , имеющая вторую производную
, имеющая вторую производную ![math]() на некотором интервале
на некотором интервале ![math]() , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале
 , имеющая вторую производную
, имеющая вторую производную  на некотором интервале
на некотором интервале  , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале
(4) любая ![math]() , имеющая вторую производную
, имеющая вторую производную ![math]() на некотором интервале
на некотором интервале ![math]() , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале
 , имеющая вторую производную
, имеющая вторую производную  на некотором интервале
на некотором интервале  , выпукла вверх или вниз на этом интервале
, выпукла вверх или вниз на этом интервале Для каких функций прямая ![math]() является вертикальной асимптотой:
является вертикальной асимптотой:
 является вертикальной асимптотой:
является вертикальной асимптотой:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Из предложенного списка выбрать те условия, которым должна удовлетворять функция ![math]() , чтобы уравнение
, чтобы уравнение ![math]() на отрезке
на отрезке ![math]() имело единственное решение:
имело единственное решение:
 , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке  имело единственное решение:
имело единственное решение:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]() на
на ![math]() или
или ![math]()
 на
на  или
или 
(6) ![math]() на
на ![math]() и
и ![math]()
 на
на  и
и 
(7) ![math]() на
на ![math]() или
или ![math]()
 на
на  или
или 
(8) ![math]() на
на ![math]() и
и ![math]()
 на
на  и
и 
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

(5) функция убывает на ![math]()

(6) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Из всех прямоугольников, площадь которых равна 9, найти прямоугольник с наименьшим периметром. В ответе укажите максимальную длину его стороны.
3
Разность двух чисел равна 10. Найдите эти числа, если известно, что их произведение принимает наименьшее значение. В ответе укажите сумму этих чисел.
0
Укажите область определения функции![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) R
Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Какое из предложенных числовых множеств является конечным:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) множество нечётных простых чисел
Если функция ![math]() определена в
определена в ![math]() - окрестности точки
- окрестности точки ![math]() и
и ![math]() , то в некоторой окрестности точки
, то в некоторой окрестности точки ![math]() функция
функция
 определена в
определена в  - окрестности точки
- окрестности точки  и
и  , то в некоторой окрестности точки
, то в некоторой окрестности точки  функция
функция
(1) не ограничена
(2) ограничена сверху
(3) ограничена
(4) ограничена снизу
Если ![math]() - б.м.ф. при
- б.м.ф. при ![math]() , а функция
, а функция ![math]() ограничена в окрестности
ограничена в окрестности ![math]() , то предел произведения
, то предел произведения ![math]()
 - б.м.ф. при
- б.м.ф. при  , а функция
, а функция  ограничена в окрестности
ограничена в окрестности  , то предел произведения
, то предел произведения 
(1) не существует
(2) равен нулю
(3) не равен нулю
(4) равен бесконечности
Указать числовой промежуток, на котором функция ![math]() непрерывна:
непрерывна:
 непрерывна:
непрерывна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() и
и ![math]() , то
, то
 непрерывна на отрезке
непрерывна на отрезке  и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Тогда
. Тогда
 . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

4/7
Вычислить![math]()

2/3
Вычислить![math]() .
.
 .
.
3
Дана сходящаяся последовательность ![math]() . Если
. Если ![math]() , то
, то
 . Если
. Если  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

4
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
1
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Правой производной ![math]() функции
функции ![math]() в данной точке
в данной точке ![math]() называется
называется
 функции
функции  в данной точке
в данной точке  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная показательной функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть задана функция ![math]() . Отметьте верные утверждения:
. Отметьте верные утверждения:
 . Отметьте верные утверждения:
. Отметьте верные утверждения:
(1) функция определена на отрезке ![math]()

(2) является обратной для функции![math]() на
на ![math]()
 на
на 
(3) убывает в области определения
(4) производная равна![math]() на интервале
на интервале ![math]()
 на интервале
на интервале 
Если последовательность ![math]() такова, что
такова, что ![math]() неравенство
неравенство ![math]() выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел ![math]() равен
равен
 такова, что
такова, что  неравенство
неравенство  выполняется лишь для конечного числа членов последовательности, то её предел
выполняется лишь для конечного числа членов последовательности, то её предел  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()
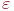
Производная ![math]() -го порядка
-го порядка ![math]() суммы двух функций
суммы двух функций ![math]() равна
равна
 -го порядка
-го порядка  суммы двух функций
суммы двух функций  равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
4
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
(1) ![math]()

(2)
![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ,
,  ,
, 
0.0476
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ,
,  ,
, 
0.0476
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какое условие теоремы Ролля не выполняется для функции ![math]() :
:
 :
:
(1) непрерывность на ![math]()

(2) дифференцируемость на ![math]()

(3) ![math]()

Пусть выполнены условия теоремы 4 (правило Лопиталя) для бесконечно малых функций ![math]() и
и ![math]() . Тогда предел
. Тогда предел ![math]()
 и
и  . Тогда предел
. Тогда предел 
(1) не существует
(2) равен ![math]()

(3) равен ![math]()

(4) равен нулю
(5) равен бесконечности
Какое выражение является многочленом Тейлора ![math]() для
для ![math]() раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки ![math]() функции
функции ![math]()
 для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки  функции
функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() .
.
 задана на отрезке
задана на отрезке  .
.
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решить уравнение ![math]()

(1) 1
(2) -1
(3) 2
(4) -2
(5) 0
(6) 3
(7) -3
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
2
Указать интервалы монотонности функции ![math]()

(1) возрастает на ![math]()

(2) возрастает на ![math]()

(3) убывает на ![math]() и возрастает на
и возрастает на ![math]()
 и возрастает на
и возрастает на 
(4) убывает на ![math]()

(5) возрастает на ![math]() и
и ![math]()
 и
и 
(6) убывает на ![math]() и
и ![math]()
 и
и 
Точка ![math]() является точкой перегиба кривой
является точкой перегиба кривой ![math]() , если в этой точке
, если в этой точке
 является точкой перегиба кривой
является точкой перегиба кривой  , если в этой точке
, если в этой точке
(1) направление выпуклости меняется
(2) направление выпуклости не меняется
Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то ![math]() равно
равно
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое условие должно выполняться в точке ![math]() , чтобы при применении метода касательных точка пересечения касательной с осью
, чтобы при применении метода касательных точка пересечения касательной с осью ![math]() было приближением к корню уравнения
было приближением к корню уравнения ![math]() на отрезке
на отрезке ![math]() :
:
 , чтобы при применении метода касательных точка пересечения касательной с осью
, чтобы при применении метода касательных точка пересечения касательной с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
-1
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
1.5
Решить уравнение ![math]()

(1) -1
(2) 1
(3) 5
(4) -5
(5) 2
(6) 3
(7) -2
(8) -3
(9) 4
(10) -4
Найти точку перегиба функции ![math]() .
.
 .
.
1
Найти точку перегиба функции ![math]() .
.
 .
.
1
Укажите область определения функции ![math]()

(1) R\ 0
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Пусть ![math]() и
и ![math]() . Какая из записей неверна:
. Какая из записей неверна:
 и
и  . Какая из записей неверна:
. Какая из записей неверна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если ![math]() для
для ![math]() и
и ![math]() , то
, то
 для
для  и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какое свойство функции ![math]() является достаточным для того, чтобы функция
является достаточным для того, чтобы функция ![math]() являлась бесконечно малой при
являлась бесконечно малой при ![math]() (
(![math]() - б.м.ф. при
- б.м.ф. при ![math]() ):
):
 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):
(1) периодичность
(2) нечётность
(3) ограниченность
Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() то
то
 непрерывна на отрезке
непрерывна на отрезке  то
то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() .
.
 .
.
3/5
Даны две сходящиеся последовательности: ![math]() . Предел последовательности
. Предел последовательности ![math]() равен
равен
 . Предел последовательности
. Предел последовательности  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

-5/2
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие из функций имеют равные правые и левые производные в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() имеет конечный предел, то эта последовательность
имеет конечный предел, то эта последовательность
 имеет конечный предел, то эта последовательность
имеет конечный предел, то эта последовательность
(1) ограничена сверху, но не ограничена снизу
(2) ограничена снизу, но не ограничена сверху
(3) ограничена
(4) неограниченна
Дифференциалом ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() называется
называется
 -го порядка
-го порядка  функции
функции  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

На линии ![math]() найти точку, в которой касательная к этой линии параллельна прямой
найти точку, в которой касательная к этой линии параллельна прямой ![math]()
 найти точку, в которой касательная к этой линии параллельна прямой
найти точку, в которой касательная к этой линии параллельна прямой 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Под каким углом кривая ![math]() пересекает ось
пересекает ось ![math]()
 пересекает ось
пересекает ось 
45
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ,
,  ,
, 
0.0504
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0999
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Геометрический смысл теоремы Ролля состоит в том, что существует хотя бы одна точка графика функции ![math]() , в которой касательная
, в которой касательная
 , в которой касательная
, в которой касательная
(1) параллельна оси ![math]()

(2) параллельна оси ![math]()

(3) перпендикулярна оси ![math]()

(4) перпендикулярна оси ![math]()

(5) параллельна хорде ![math]()

Какие утверждения справедливы:
(1) если ![math]() и
и ![math]() - бесконечно малые в точке
- бесконечно малые в точке ![math]() функции и существует предел
функции и существует предел ![math]() , то существует также предел
, то существует также предел ![math]() ;
;
 и
и  - бесконечно малые в точке
- бесконечно малые в точке  функции и существует предел
функции и существует предел  , то существует также предел
, то существует также предел  ;
;
(2) для бесконечно малых в точке ![math]() функций
функций ![math]() и
и ![math]() , у которых и существует предел
, у которых и существует предел ![math]() , также существует предел
, также существует предел ![math]() ;
;
 функций
функций  и
и  , у которых и существует предел
, у которых и существует предел  , также существует предел
, также существует предел  ;
;
(3) если ![math]() и
и ![math]() - бесконечно большие в точке
- бесконечно большие в точке ![math]() функции и существует предел
функции и существует предел ![math]() , то существует также предел
, то существует также предел ![math]() ;
;
 и
и  - бесконечно большие в точке
- бесконечно большие в точке  функции и существует предел
функции и существует предел  , то существует также предел
, то существует также предел  ;
;
(4) для бесконечно больших в точке ![math]() функций
функций ![math]() и
и ![math]() , у которых и существует предел
, у которых и существует предел ![math]() , также существует предел
, также существует предел ![math]() ;
;
 функций
функций  и
и  , у которых и существует предел
, у которых и существует предел  , также существует предел
, также существует предел  ;
; Какая из формул является выражением для остаточного члена ![math]() в форме Лагранжа
в форме Лагранжа
 в форме Лагранжа
в форме Лагранжа
(1) ![math]()

(2) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) 0
(7) 2
(8) 1
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/6
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
5/24
Точка ![math]() называется точкой локального максимума функции
называется точкой локального максимума функции ![math]() , если
, если
 называется точкой локального максимума функции
называется точкой локального максимума функции  , если
, если
(1) ![math]()
![math]()


(2) ![math]()
![math]()


(3) ![math]()
![math]()


(4) ![math]()
![math]()


Какие условия являются достаточными, чтобы точка ![math]() была точкой перегиба кривой
была точкой перегиба кривой ![math]()
 была точкой перегиба кривой
была точкой перегиба кривой 
(1) ![math]() при
при ![math]() и
и ![math]() при
при ![math]()
 при
при  и
и  при
при 
(2) ![math]() при
при ![math]() и
и ![math]() при
при ![math]()
 при
при  и
и  при
при 
(3) ![math]() при
при ![math]() и
и ![math]() при
при ![math]()
 при
при  и
и  при
при 
(4) ![math]() при
при ![math]() и
и ![math]() при
при ![math]()
 при
при  и
и  при
при 
Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то ![math]() равно
равно
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Второе приближение ![math]() корня уравнения
корня уравнения ![math]() на отрезке
на отрезке ![math]() методом хорд вычисляется по формуле:
методом хорд вычисляется по формуле:
 корня уравнения
корня уравнения  на отрезке
на отрезке  методом хорд вычисляется по формуле:
методом хорд вычисляется по формуле:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
-5
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
0.25
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
2
Найти точку перегиба функции ![math]() .
.
 .
.
2
Укажите область определения функции ![math]()

(1) R
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Число ![math]() является
является
 является
является
(1) целым
(2) рациональным
(3) иррациональным
(4) натуральным
По определению, ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![math]() и
и ![math]() . Тогда (
. Тогда (![math]() - б.м.ф. при
- б.м.ф. при ![math]() )
)
 определена в некоторой окрестности точки
определена в некоторой окрестности точки  и
и  . Тогда (
. Тогда ( - б.м.ф. при
- б.м.ф. при  )
)
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() , то она на нём
, то она на нём
 непрерывна на отрезке
непрерывна на отрезке  , то она на нём
, то она на нём
(1) ограничена
(2) ограничена сверху, но не ограничена снизу
(3) ограничена снизу, но не ограничена сверху
(4) не ограничена
Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

2
Вычислить![math]()

2
Вычислить![math]() .
.
 .
.
1/2
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

0
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() с помощью логарифмического дифференцирования вычисляется по
с помощью логарифмического дифференцирования вычисляется по
 с помощью логарифмического дифференцирования вычисляется по
с помощью логарифмического дифференцирования вычисляется по
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется невозрастающей, если
называется невозрастающей, если ![math]()
 называется невозрастающей, если
называется невозрастающей, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана параметрически:
задана параметрически: ![math]() . Чему равна производная
. Чему равна производная ![math]() :
:
 задана параметрически:
задана параметрически:  . Чему равна производная
. Чему равна производная  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

1.0033
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

1.9983
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какое выражение является формулой Лагранжа для функции ![math]() на отрезке [a,b]:
на отрезке [a,b]:
 на отрезке [a,b]:
на отрезке [a,b]:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Проверить выполнение условий теоремы 6 для применения правила Лопиталя при вычислении предела ![math]()

(1) ![math]() - бесконечно большая и -
- бесконечно большая и - ![math]() бесконечно большая
бесконечно большая
 - бесконечно большая и -
- бесконечно большая и -  бесконечно большая
бесконечно большая
(2) ![math]() и
и ![math]() дифференцируемы в окрестности точки
дифференцируемы в окрестности точки ![math]()
 и
и  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 
(3) существует ![math]()

Какая их формул является разложением Маклорена для функции ![math]() c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
17
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
95
Для каких функций точка ![math]() является точкой локального минимума:
является точкой локального минимума:
 является точкой локального минимума:
является точкой локального минимума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для каких функций точка перегиба имеет абсциссу ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , если
, если
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
0
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
1
Указать наименьший элемент множества ![math]()

-3
Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) -2
(4) 3
(5) 1.5
(6) 0
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вверх?
является выпуклой вверх?
 является выпуклой вверх?
является выпуклой вверх?
(1) 2
(2) 3
(3) 4
(4) 5
(5) 6
(6) 7
Укажите область определения функции ![math]()

(1) R
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Выражение ![math]() равно
равно
 равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая из функций имеет предел на бесконечности, равный нулю:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть функции ![math]() определены в некоторой окрестности точки
определены в некоторой окрестности точки ![math]() и
и ![math]() . Тогда
. Тогда
 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и  . Тогда
. Тогда
(1) ![math]() , если
, если ![math]()
 , если
, если 
(2) ![math]() , если
, если ![math]()
 , если
, если 
(3) ![math]() , если
, если ![math]()
 , если
, если 
Отметьте верные формулы:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() , то
, то
 непрерывна на отрезке
непрерывна на отрезке  , то
, то
(1) она на этом отрезке принимает свои наименьшее и наибольшее значения
(2) она на этом отрезке не достигает своей точной верхней или нижней грани
(3) ![math]()

Пусть ![math]() - бесконечно малые при
- бесконечно малые при ![math]() функции, причём
функции, причём ![math]() и
и ![math]() . Если
. Если ![math]() , то
, то
 - бесконечно малые при
- бесконечно малые при  функции, причём
функции, причём  и
и  . Если
. Если  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

-1/16
Вычислить![math]()

-1/12
Вычислить![math]() .
.
 .
.
3/4
Вычислить![math]()

-2/3
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
1/2
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
-2
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

(6) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Если функция ![math]() в точке
в точке ![math]() имеет бесконечную производную
имеет бесконечную производную ![math]() , то касательная, проведённая к кривой
, то касательная, проведённая к кривой ![math]() в точке
в точке ![math]()
 в точке
в точке  имеет бесконечную производную
имеет бесконечную производную  , то касательная, проведённая к кривой
, то касательная, проведённая к кривой  в точке
в точке 
(1) перпендикулярна оси Ox
(2) перпендикулярна оси Oy
(3) параллельна оси Oy
(4) пересекает ось Ox под углом ![math]()

Чему равна производная сложной функции ![math]() в точке
в точке ![math]() :
:
 в точке
в точке  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Приближённое значение функции ![math]() в точке
в точке ![math]() равно
равно
 в точке
в точке  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() ,
, ![math]() является
является
 ,
,  является
является
(1) возрастающей
(2) убывающей
(3) немонотонной
Постоянный вектор ![math]() называется пределом вектор-функции
называется пределом вектор-функции ![math]() при
при ![math]()
 называется пределом вектор-функции
называется пределом вектор-функции  при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.995
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.9975
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какое условие нужно добавить к теореме Лагранжа, чтобы выполнялась теорема Ролля:
(1) непрерывность на ![math]()

(2) непрерывность на ![math]()

(3) ограниченность на ![math]()

(4) монотонность на ![math]()

(5) дифференцируемость на ![math]()

(6) дифференцируемость в точке ![math]()

(7) ![math]()

(8) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
34
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
30
Функция ![math]() может иметь экстремум только в тех точках, в которых её производная
может иметь экстремум только в тех точках, в которых её производная ![math]()
 может иметь экстремум только в тех точках, в которых её производная
может иметь экстремум только в тех точках, в которых её производная 
(1) не существует
(2) равна 0
(3) не равна 0
(4) равна 0 или не существует
(5) равна ![math]()

(6) не равна нулю или не существует
(7) равна нулю или ![math]()

Прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , если
, если
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

Найти значение ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
1
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
-4
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) -2
(2) -1
(3) 1
(4) точек перегиба нет
(5) 0.5
(6) 2
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 2
(2) 3
(3) -2
(4) точек перегиба нет
(5) 1
(6) 0
Укажите область определения функции ![math]()

(1) R\ 0
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/2
Пусть ![math]() . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
 . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Отметьте верные утверждения
(1) определение непрерывности по Коши и по Гейне эквивалентны
(2) если функция![math]() непрерывна в точке
непрерывна в точке ![math]() , то функции
, то функции ![math]() и
и![math]() непрерывны в этой точке
непрерывны в этой точке
 непрерывна в точке
непрерывна в точке  , то функции
, то функции  и
и непрерывны в этой точке
непрерывны в этой точке
(3) если функции![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]() , то функции
, то функции ![math]() непрерывна в этой точке
непрерывна в этой точке
 и
и  непрерывны в точке
непрерывны в точке  , то функции
, то функции  непрерывна в этой точке
непрерывна в этой точке Если ![math]() - б.м.ф. при
- б.м.ф. при ![math]() ,
, ![math]() и
и ![math]() , то
, то
 - б.м.ф. при
- б.м.ф. при  ,
,  и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

0
Вычислить![math]()

0
Вычислить![math]() .
.
 .
.
-4/3
Вычислить![math]()

-11/6
Вычислить предел, используя асимптотические формулы ![math]()

-4
Вычислить предел, используя асимптотические формулы ![math]()

2
Для каких из перечисленных функций ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Чему равна производная функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() возрастает, то ее неограниченность означает, что
возрастает, то ее неограниченность означает, что ![math]() равен
равен
 возрастает, то ее неограниченность означает, что
возрастает, то ее неограниченность означает, что  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производной вектор-функции ![math]() по её аргументу
по её аргументу ![math]() называется
называется
 по её аргументу
по её аргументу  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть закон радиоактивного распада вещества записывается следующим образом: ![math]() . Чему равна скорость распада
. Чему равна скорость распада ![math]() в момент времени
в момент времени ![math]() ?
?
 . Чему равна скорость распада
. Чему равна скорость распада  в момент времени
в момент времени  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Смещение груза на пружине описывается законом ![math]() . Найдите скорость тела в момент времени
. Найдите скорость тела в момент времени ![math]() .
.
 . Найдите скорость тела в момент времени
. Найдите скорость тела в момент времени  .
.
10
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.01
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.02
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) -1
(2) -2
(3) 0
(4) ![math]()

(5) ![math]()

(6) 1
Вычислить предел ![math]()

-1
Вычислить предел ![math]()

-2
Для каких функций точка ![math]() является точкой экстремума:
является точкой экстремума:
 является точкой экстремума:
является точкой экстремума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Прямая ![math]() является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции ![math]() , если
, если
 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]() или
или ![math]()
 или
или 
(4) ![math]()

С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) 4
(4) -2
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 6
(2) точек перегиба нет
(3) 4
(4) 3
(5) 1
(6) 0
Укажите область определения функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Для модуля ![math]() произведения двух чисел выбрать справедливое утверждение:
произведения двух чисел выбрать справедливое утверждение:
 произведения двух чисел выбрать справедливое утверждение:
произведения двух чисел выбрать справедливое утверждение:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие условия являются достаточными для того, чтобы предел сложной функции ![math]() существовал:
существовал:
 существовал:
существовал:
(1) существует![math]() и
и ![math]() непрерывна в точке
непрерывна в точке ![math]()
 и
и  непрерывна в точке
непрерывна в точке 
(2) существует![math]() и
и ![math]() разрывна в точке
разрывна в точке ![math]()
 и
и  разрывна в точке
разрывна в точке 
(3) существует![math]() и
и ![math]() непрерывна в точке
непрерывна в точке ![math]()
 и
и  непрерывна в точке
непрерывна в точке 
Функция ![math]() при
при ![math]() , если
, если
 при
при  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

-1
Вычислить![math]()

1/2
Вычислить предел, используя асимптотические формулы ![math]()

-1/2
Вычислить предел, используя асимптотические формулы ![math]()

2
Функция ![math]() называется дифференцируемой в точке
называется дифференцируемой в точке ![math]() , если приращение
, если приращение ![math]() можно представить в виде (
можно представить в виде (![math]() )
)
 называется дифференцируемой в точке
называется дифференцируемой в точке  , если приращение
, если приращение  можно представить в виде (
можно представить в виде ( )
)
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для сходимости монотонной последовательности достаточно (и необходимо), чтобы она была
(1) ограниченной
(2) неограниченной
(3) ограниченной сверху
(4) ограниченной снизу
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0025
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0025
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени  ?
?
-4
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() скорость точки была равна
скорость точки была равна ![math]() м/с?
м/с?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  скорость точки была равна
скорость точки была равна  м/с?
м/с?
1
Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
6
При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
0.1
Пусть ![math]() - критическая точка
- критическая точка ![math]() , но
, но ![math]() непрерывна в
непрерывна в ![math]() . Тогда функция
. Тогда функция ![math]() в точке
в точке ![math]() имеет максимум, если её производная
имеет максимум, если её производная ![math]() при переходе через точку
при переходе через точку ![math]()
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет максимум, если её производная
имеет максимум, если её производная  при переходе через точку
при переходе через точку 
(1) меняет знак с минуса на плюс
(2) меняет знак с плюса на минус
(3) не меняет знак
Какие утверждения справедливы:
(1) график функции никогда не пересекает асимптоту
(2) график функции может пересекать асимптоту только в одной точке
(3) график функции может пересекать асимптоту хотя бы в одной точке
(4) наклонные асимптоты при ![math]() и
и ![math]() всегда совпадают
всегда совпадают
 и
и  всегда совпадают
всегда совпадают
(5) наклонные асимптоты при ![math]() и
и ![math]() могут совпадать
могут совпадать
 и
и  могут совпадать
могут совпадать С помощью производной определите, какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

0
Найти точку перегиба функции ![math]()

0
Укажите область определения функции ![math]()

(1) R
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Какое подмножество числовой прямой равносильно неравенству ![math]() :
:
 :
:
(1) интервал ![math]()

(2) полуинтервал ![math]()

(3) интервал ![math]()

Если функция ![math]() - бесконечно большая функция при
- бесконечно большая функция при ![math]() , то функция
, то функция ![math]()
 - бесконечно большая функция при
- бесконечно большая функция при  , то функция
, то функция 
(1) бесконечно большая
(2) бесконечно малая
(3) неограниченная
Как представить функцию ![math]() в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций ![math]() и
и ![math]()
 в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций  и
и 
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Что является асимптотической формулой для ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

1/5
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Какие из перечисленных функций дифференцируемы в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если последовательность ![math]() ограниченная, то она
ограниченная, то она
 ограниченная, то она
ограниченная, то она
(1) сходится
(2) содержит сходящуюся подпоследовательность
(3) расходится
(4) содержит расходящуюся подпоследовательность
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.01
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0125
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти ![math]()
![math]()


0.1
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

2
Пусть в точке ![math]() функция
функция ![math]() имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
 функция
функция  имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
(1) если ![math]() , то
, то ![math]() - точка максимума для
- точка максимума для ![math]()
 , то
, то  - точка максимума для
- точка максимума для 
(2) если ![math]() , то
, то ![math]() - точка максимума для
- точка максимума для ![math]()
 , то
, то  - точка максимума для
- точка максимума для 
(3) если ![math]() - точка максимума для
- точка максимума для ![math]() , то
, то ![math]()
 - точка максимума для
- точка максимума для  , то
, то 
(4) если ![math]() - точка максимума для
- точка максимума для ![math]() , то
, то ![math]()
 - точка максимума для
- точка максимума для  , то
, то 
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Укажите область определения функции ![math]()

(1) R
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите горизонтальную асимптоту графика функции ![math]()

(1) ![math]()

(2) нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Какое из перечисленных ниже множеств является окрестностью точки ![math]()

(1) полуинтервал ![math]()

(2) интервал ![math]()

(3) полуинтервал ![math]()

(4) интервал ![math]()

Число А называется пределом функции ![math]() слева
слева ![math]() , если
, если
 слева
слева  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

4
Вычислить![math]()

11/7
Дифференциалом ![math]() функции
функции ![math]() называется
называется
 функции
функции  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.5075
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.4969
Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 2Z - Множество четных целых чисел
(2) множество натуральных чисел, являющихся квадратами ![math]()

(3) множество рациональных чисел Q
(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 ; убывает на
; убывает на  и
и 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]()

(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/8
Какое из неравенств задаёт ![math]() -окрестность точки
-окрестность точки ![math]()
 -окрестность точки
-окрестность точки 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() , тогда
, тогда
 , тогда
, тогда
(1) ![math]()

(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/2
Вычислить![math]()

7
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть функция ![math]() задана на отрезке
задана на отрезке ![math]() . Определить количество корней уравнения
. Определить количество корней уравнения ![math]() на интервале
на интервале ![math]()
 задана на отрезке
задана на отрезке  . Определить количество корней уравнения
. Определить количество корней уравнения  на интервале
на интервале 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точную верхнюю грань множества ![math]()

2
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 ; убывает на
; убывает на  и
и 
(4) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 и
и  ; убывает на
; убывает на  и
и 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 и
и  ; убывает на
; убывает на  и
и 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

3
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
-2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-2/3
Какое из перечисленных ниже множеств является множеством всех верхних граней для ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть задана функция ![math]() . Тогда
. Тогда
 . Тогда
. Тогда
(1) предел слева ![math]() равен 1
равен 1
 равен 1
равен 1
(2) предел справа ![math]() не существует
не существует
 не существует
не существует
(3) предел ![math]() существует
существует
 существует
существует Вычислить![math]()

1
Вычислить![math]()

8
Вычислить предел данной последовательности: ![math]()

(1) 2
(2) 1
(3) 0
(4) ![math]()

(5) -5
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти точную нижнюю грань множества ![math]()

-2
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Какие из перечисленных ниже множеств являются ограниченными сверху множествами:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

2
Вычислить![math]()

0
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
-1
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
3
Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
2
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
6
Найти точную верхнюю грань множества ![math]()

1/4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Если ![math]() - точная верхняя грань множества
- точная верхняя грань множества ![math]() , то эта грань
, то эта грань
 - точная верхняя грань множества
- точная верхняя грань множества  , то эта грань
, то эта грань
(1) наименьшая нижняя
(2) наибольшая верхняя
(3) наименьшая верхняя
(4) наибольшая нижняя
Вычислить![math]()

1/3
Вычислить![math]()

0
Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 3
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
5/7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Пусть задано множество ![math]() .Отметьте верные утверждения
.Отметьте верные утверждения
 .Отметьте верные утверждения
.Отметьте верные утверждения
(1) множество ![math]() бесконечно
бесконечно
 бесконечно
бесконечно
(2) множество всех верхних граней ![math]() пусто
пусто
 пусто
пусто
(3) точная нижняя грань множества ![math]() равна
равна![math]()
 равна
равна
(4) множество ![math]() ограничено
ограничено
 ограничено
ограничено Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
1
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
3
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/4
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
51/10
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 2
(2) 3
(3) 6
(4) 8
(5) 9
(6) 12
Какие из множеств являются подмножеством множества ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Указать область определения функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() называется бесконечно большой функцией при
называется бесконечно большой функцией при ![math]() , стремящемся к
, стремящемся к ![math]() , если
, если ![math]() равен
равен
 называется бесконечно большой функцией при
называется бесконечно большой функцией при  , стремящемся к
, стремящемся к  , если
, если  равен
равен
(1) ![math]()

(2) 0
(3) ![math]()

(4) не существует
По определению ![math]() , функция
, функция ![math]() называется непрерывной в точке
называется непрерывной в точке ![math]() , если
, если
 , функция
, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() , то односторонние пределы в этой точке
, то односторонние пределы в этой точке
 непрерывна в точке
непрерывна в точке  , то односторонние пределы в этой точке
, то односторонние пределы в этой точке
(1) не равны
(2) равны ![math]()

(3) не существуют
Пусть для функции ![math]() выполнено условие
выполнено условие ![math]() . Это означает, что функция
. Это означает, что функция ![math]()
 выполнено условие
выполнено условие  . Это означает, что функция
. Это означает, что функция 
(1) непрерывна на интервале ![math]()

(2) равномерно непрерывна на интервале ![math]()

(3) непрерывна на отрезке ![math]()

(4) равномерно непрерывна на отрезке ![math]()

Вычислить![math]()

-7
Вычислить![math]()

7
Вычислить![math]()

2
Десятый член последовательности ![math]() равен
равен
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3/2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]() если
если ![math]() и
и ![math]()
 - целая часть от
- целая часть от  .
.  если
если  и
и 
(1) да
(2) нет
Какие равенства верны:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() , где
, где ![math]()
 , где
, где 
Какая из перечисленных функций является обратной для функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется ограниченной снизу, если
называется ограниченной снизу, если ![math]()
 называется ограниченной снизу, если
называется ограниченной снизу, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() есть
есть
 -го порядка
-го порядка  функции
функции  есть
есть
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
13
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
9
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Каким условиям должна удовлетворять функция ![math]() в теореме Лагранжа:
в теореме Лагранжа:
 в теореме Лагранжа:
в теореме Лагранжа:
(1) непрерывность на ![math]()

(2) непрерывность на ![math]()

(3) ограниченность на ![math]()

(4) монотонность на ![math]()

(5) дифференцируемость на ![math]()

(6) дифференцируемость в точке ![math]()

(7) ![math]()

(8) ![math]()

Какую неопределённость нужно раскрыть при вычислении предела функции ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какое выражение является формулой Маклорена для многочлена степени ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
3
Вычислить ![math]()

0
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/45
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-9
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-3
Функция ![math]() называется невозрастающей на [a,b], если
называется невозрастающей на [a,b], если ![math]()
 называется невозрастающей на [a,b], если
называется невозрастающей на [a,b], если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Наименьшее значение функция ![math]() может принимать
может принимать
 может принимать
может принимать
(1) только на концах отрезка
(2) только в точках локального минимума
(3) на концах отрезка или в точках локального минимума
(4) на концах отрезка и в точках локального минимума
Прямая ![math]() является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции ![math]() только в том случае, если
только в том случае, если
 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  только в том случае, если
только в том случае, если
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() или
или ![math]()
 или
или 
(3) ![math]() или
или ![math]()
 или
или 
(4) ![math]() и
и ![math]()
 и
и 
(5) ![math]() или
или ![math]()
 или
или 
Пусть для функции ![math]() в окрестности точки
в окрестности точки ![math]() существует производная
существует производная ![math]() -го порядка и
-го порядка и ![math]() - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда ![math]() - точка минимуа
- точка минимуа ![math]() , если
, если
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и  - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка минимуа
- точка минимуа  , если
, если
(1) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(2) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(3) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
(4) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
С помощью производной найти значение выражения ![math]() .
.
 .
.
-0.5
С помощью производной найти значение выражения ![math]() .
.
 .
.
-0.5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
17/33
Найти наибольшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
10
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
-32
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
2/5
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
1/117
Пусть ![math]() - множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество
- множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество ![math]() :
:
 - множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество
- множество натуральных делителей 8, не равных 1. Какое из перечисленных множеств есть множество  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению (Коши),![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая из перечисленных функций является б.м.ф. при ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие из перечисленных функций непрерывны в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Точка ![math]() называется точкой разрыва функции
называется точкой разрыва функции ![math]() с конечным скачком функции, если в точке
с конечным скачком функции, если в точке ![math]()
 называется точкой разрыва функции
называется точкой разрыва функции  с конечным скачком функции, если в точке
с конечным скачком функции, если в точке 
(1) конечные пределы слева и справа равны
(2) конечные пределы слева и справа не равны
(3) конечный предел слева или справа не существует
Вычислить![math]()

3/4
Вычислить![math]()

2
Вычислить![math]()

3
По определению, число ![math]() называется пределом последовательности
называется пределом последовательности ![math]() , если
, если ![math]() справедливо неравенство
справедливо неравенство
 называется пределом последовательности
называется пределом последовательности  , если
, если  справедливо неравенство
справедливо неравенство
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Производной функции![math]() является функция
является функция
 является функция
является функция
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какому условию должны удовлетворять функции ![math]() , чтобы их произведение
, чтобы их произведение ![math]() было дифференцируемым:
было дифференцируемым:
 , чтобы их произведение
, чтобы их произведение  было дифференцируемым:
было дифференцируемым:
(1) ![math]() дифференцируема и
дифференцируема и ![math]() непрерывна
непрерывна
 дифференцируема и
дифференцируема и  непрерывна
непрерывна
(2) ![math]() дифференцируема и
дифференцируема и ![math]() дифференцируема
дифференцируема
 дифференцируема и
дифференцируема и  дифференцируема
дифференцируема
(3) ![math]() дифференцируема или
дифференцируема или ![math]() дифференцируема
дифференцируема
 дифференцируема или
дифференцируема или  дифференцируема
дифференцируема Каким условием должна удовлетворять функция ![math]() для того, чтобы существовала непрерывная убывающая обратная функция
для того, чтобы существовала непрерывная убывающая обратная функция ![math]() :
:
 для того, чтобы существовала непрерывная убывающая обратная функция
для того, чтобы существовала непрерывная убывающая обратная функция  :
:
(1) непрерывность и убывание на отрезке
(2) ограниченность и возрастание на отрезке
(3) непрерывность и возрастание на отрезке
(4) ограниченность и убывание на отрезке
Последовательность ![math]() , где
, где ![math]() является
является
 , где
, где  является
является
(1) ограниченной снизу
(2) ограниченной сверху
(3) неограниченной сверху
(4) неограниченной снизу
Пусть существует ![math]() -я производная
-я производная ![math]() в точке
в точке ![math]() . Существует ли производная меньшего порядка
. Существует ли производная меньшего порядка ![math]() :
:
 -я производная
-я производная  в точке
в точке  . Существует ли производная меньшего порядка
. Существует ли производная меньшего порядка  :
:
(1) да
(2) нет
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
4
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
16
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Лагранжа точка ![math]()

(1) совпадает с концами отрезка ![math]() или
или ![math]()
 или
или 
(2) лежит вне отрезка ![math]()

(3) принадлежит интервалу ![math]()

Пусть ![math]() и
и ![math]() - бесконечно большие в точке
- бесконечно большие в точке ![math]() функции, для которых существует предел
функции, для которых существует предел ![math]() . Тогда существует предел
. Тогда существует предел
 и
и  - бесконечно большие в точке
- бесконечно большие в точке  функции, для которых существует предел
функции, для которых существует предел  . Тогда существует предел
. Тогда существует предел
(1) ![math]()

(2) ![math]()

(3) ![math]()

Верно ли, что ![math]() раз дифференцируемую в окрестности точки
раз дифференцируемую в окрестности точки ![math]() функцию
функцию ![math]() можно представить в виде формулыТейлора?
можно представить в виде формулыТейлора?
 раз дифференцируемую в окрестности точки
раз дифференцируемую в окрестности точки  функцию
функцию  можно представить в виде формулыТейлора?
можно представить в виде формулыТейлора?
(1) да, всегда
(2) нет, никогда
(3) да, но есть исключения
Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 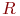 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Пусть функция ![math]() непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную ![math]() на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
 непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
(1) ![math]() на
на ![math]() невозрастающая на [a,b]
невозрастающая на [a,b]
 на
на  невозрастающая на [a,b]
невозрастающая на [a,b]
(2) ![math]() на
на ![math]() невозрастающая на [a,b]
невозрастающая на [a,b]
 на
на  невозрастающая на [a,b]
невозрастающая на [a,b]
(3) ![math]() невозрастающая на
невозрастающая на ![math]() на
на ![math]()
 невозрастающая на
невозрастающая на  на
на 
(4) ![math]() невозрастающая на
невозрастающая на ![math]() на
на ![math]()
 невозрастающая на
невозрастающая на  на
на 
График дифференцируемой на интервале ![math]() функции
функции ![math]() имеет на этом интервале выпуклость, направленную вниз, если график
имеет на этом интервале выпуклость, направленную вниз, если график ![math]() лежит в пределах интервала
лежит в пределах интервала
 функции
функции  имеет на этом интервале выпуклость, направленную вниз, если график
имеет на этом интервале выпуклость, направленную вниз, если график  лежит в пределах интервала
лежит в пределах интервала
(1) не выше любой своей касательной
(2) не ниже любой своей касательной
(3) не выше и не ниже любой своей касательной
Пусть прямая ![math]() - вертикальная асимптота функции
- вертикальная асимптота функции ![math]() . Тогда точка
. Тогда точка ![math]() может быть
может быть
 - вертикальная асимптота функции
- вертикальная асимптота функции  . Тогда точка
. Тогда точка  может быть
может быть
(1) только точкой разрыва функции
(2) точкой разрыва функции
(3) только концом области определения функции
(4) концом области определения функции
Для функции ![math]() точка (0,0) графика функции является
точка (0,0) графика функции является
 точка (0,0) графика функции является
точка (0,0) графика функции является
(1) точкой максимума
(2) точкой минимума
(3) точкой перегиба
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 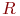 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-3
Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-8
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) точек разрыва нет
(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) y=2x-2
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) нет
(6) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть ![math]() и
и ![math]() . Какое множество является объединением
. Какое множество является объединением ![math]()
 и
и  . Какое множество является объединением
. Какое множество является объединением 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() и
и ![math]() , то
, то
 и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() или
или ![math]()
 или
или 
Какое условие является достаточным для равенства нулю предела суммы двух функций ![math]() при
при ![math]() :
:
 при
при  :
:
(1) ![math]() - б.м.ф.,
- б.м.ф., ![math]() - б.м.ф.
- б.м.ф.
 - б.м.ф.,
- б.м.ф.,  - б.м.ф.
- б.м.ф.
(2) ![math]() - б.м.ф.,
- б.м.ф., ![math]() - ограниченная
- ограниченная
 - б.м.ф.,
- б.м.ф.,  - ограниченная
- ограниченная
(3) ![math]() ,
, ![math]() - б.м.ф.
- б.м.ф.
 ,
,  - б.м.ф.
- б.м.ф.
(4) ![math]() - б.м.ф.,
- б.м.ф., ![math]()
 - б.м.ф.,
- б.м.ф., 
Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() и
и ![math]() ,то
,то
 непрерывна в точке
непрерывна в точке  и
и  ,то
,то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Точка ![math]() для функции
для функции ![math]() является точкой разрыва
является точкой разрыва
 для функции
для функции  является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть ![math]() б.м.ф. при
б.м.ф. при ![math]() и
и ![math]() . Тогда
. Тогда
 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

4
Вычислить![math]()

2
Вычислить![math]()

2
Последовательность ![math]() является
является
 является
является
(1) сходящейся
(2) расходящейся
Вычислить![math]()

2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
0
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
e
Угловой коэффициент касательной, проведённой к кривой ![math]() в точке с абсциссой
в точке с абсциссой ![math]() , равен
, равен
 в точке с абсциссой
в точке с абсциссой  , равен
, равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое равенство верно (![math]() ):
):
 ):
):
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функции ![math]() и
и ![math]() взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
 и
и  взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
(1) если производная ![math]() конечна, то производная обратной функции в соответствующей точке тоже конечна
конечна, то производная обратной функции в соответствующей точке тоже конечна
 конечна, то производная обратной функции в соответствующей точке тоже конечна
конечна, то производная обратной функции в соответствующей точке тоже конечна
(2) касательные взаимно обратных функций совпадают
(3) касательная к графику функции ![math]() в точке
в точке ![math]() является касательной к графику обратной функции, если она не параллельна оси
является касательной к графику обратной функции, если она не параллельна оси![math]()
 в точке
в точке  является касательной к графику обратной функции, если она не параллельна оси
является касательной к графику обратной функции, если она не параллельна оси
Последовательность ![math]() называется бесконечно малой, если
называется бесконечно малой, если ![math]() равен
равен
 называется бесконечно малой, если
называется бесконечно малой, если  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()
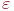
Чему равна ![math]() -я производная функции
-я производная функции ![math]()
 -я производная функции
-я производная функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
3
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
2
Дано уравнение ![math]() . Найти сумму абсцисс точек на кривой, в которой касательная параллельна прямой.
. Найти сумму абсцисс точек на кривой, в которой касательная параллельна прямой.
 . Найти сумму абсцисс точек на кривой, в которой касательная параллельна прямой.
. Найти сумму абсцисс точек на кривой, в которой касательная параллельна прямой.
0
К графику функции ![math]() в точке с абсциссой
в точке с абсциссой ![math]() проведена касательная. Найти абсциссу точки пересечения касательной с осью Ox.
проведена касательная. Найти абсциссу точки пересечения касательной с осью Ox.
 в точке с абсциссой
в точке с абсциссой  проведена касательная. Найти абсциссу точки пересечения касательной с осью Ox.
проведена касательная. Найти абсциссу точки пересечения касательной с осью Ox.
-4
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Лагранжа точка ![math]()

(1) совпадает с концами отрезка ![math]() или
или ![math]()
 или
или 
(2) лежит вне отрезка ![math]()

(3) принадлежит интервалу ![math]()

Каким условиям в точке ![math]() должны удовлетворять функции
должны удовлетворять функции ![math]() и
и ![math]() , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
 должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
(1) ![math]() - бесконечно большая и
- бесконечно большая и ![math]() - бесконечно малая
- бесконечно малая
 - бесконечно большая и
- бесконечно большая и  - бесконечно малая
- бесконечно малая
(2) ![math]() - бесконечно малая и -
- бесконечно малая и - ![math]() бесконечно большая
бесконечно большая
 - бесконечно малая и -
- бесконечно малая и -  бесконечно большая
бесконечно большая
(3) ![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]()
 и
и  непрерывны в точке
непрерывны в точке 
(4) ![math]() и
и ![math]() дифференцируемы в проколотой окрестности точки
дифференцируемы в проколотой окрестности точки ![math]()
 и
и  дифференцируемы в проколотой окрестности точки
дифференцируемы в проколотой окрестности точки 
(5) существует ![math]()

(6) существует ![math]()

Верно ли, что функция ![math]() раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки ![math]()
 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 
(1) да
(2) нет
Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-1/3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-1
Пусть функция ![math]() в точке
в точке ![math]() имеет производную
имеет производную ![math]() . Какое утверждение верно:
. Какое утверждение верно:
 в точке
в точке  имеет производную
имеет производную  . Какое утверждение верно:
. Какое утверждение верно:
(1) ![math]() возрастает в точке
возрастает в точке ![math]()
 возрастает в точке
возрастает в точке 
(2) ![math]() возрастает в точке
возрастает в точке ![math]()
 возрастает в точке
возрастает в точке 
(3) ![math]() возрастает в точке
возрастает в точке ![math]()
 возрастает в точке
возрастает в точке 
(4) ![math]() возрастает в точке
возрастает в точке ![math]()
 возрастает в точке
возрастает в точке 
Выпуклость кривой ![math]() в точке
в точке ![math]() направлена вниз, если
направлена вниз, если
 в точке
в точке  направлена вниз, если
направлена вниз, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для каких функций прямая ![math]() является вертикальной асимптотой:
является вертикальной асимптотой:
 является вертикальной асимптотой:
является вертикальной асимптотой:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Из предложенного списка выбрать те условия, которым должна удовлетворять функция ![math]() , чтобы уравнение
, чтобы уравнение ![math]() на отрезке
на отрезке ![math]() имело единственное решение:
имело единственное решение:
 , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке  имело единственное решение:
имело единственное решение:
(1) ![math]() непрерывна на
непрерывна на ![math]()
 непрерывна на
непрерывна на 
(2) ![math]() непрерывна на
непрерывна на ![math]()
 непрерывна на
непрерывна на 
(3) числа ![math]() и
и ![math]() одного знака
одного знака
 и
и  одного знака
одного знака
(4) числа ![math]() и
и ![math]() разных знаков
разных знаков
 и
и  разных знаков
разных знаков
(5) ![math]() одного знака на
одного знака на ![math]()
 одного знака на
одного знака на 
(6) ![math]() , меняющая знак на
, меняющая знак на ![math]()
 , меняющая знак на
, меняющая знак на 
(7) ![math]() одного знака на
одного знака на ![math]()
 одного знака на
одного знака на 
(8) ![math]() , меняющая знак на
, меняющая знак на ![math]()
 , меняющая знак на
, меняющая знак на 
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Из всех прямоугольников, площадь которых равна 25, найти прямоугольник с наименьшим периметром. В ответе укажите максимальную длину его стороны.
5
Разность двух чисел равна 98. Найдите эти числа, если известно, что их произведение принимает наименьшее значение. В ответе укажите сумму этих чисел.
0
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) точек разрыва нет
(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) нет
(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Какое из предложенных числовых множеств является бесконечным:
(1) множество чётных простых чисел
(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое свойство функции ![math]() в некоторой окрестности точки
в некоторой окрестности точки ![math]() является необходимым для существования конечного предела
является необходимым для существования конечного предела ![math]() в точке
в точке ![math]() :
:
 в некоторой окрестности точки
в некоторой окрестности точки  является необходимым для существования конечного предела
является необходимым для существования конечного предела  в точке
в точке  :
:
(1) ограниченность снизу
(2) ограниченность сверху
(3) неограниченность
(4) ограниченность
Если ![math]() , а функция
, а функция ![math]() ограничена в окрестности
ограничена в окрестности ![math]() , то предел произведения
, то предел произведения ![math]()
 , а функция
, а функция  ограничена в окрестности
ограничена в окрестности  , то предел произведения
, то предел произведения 
(1) не существует
(2) равен нулю
(3) не равен нулю
(4) равен бесконечности
Указать числовой промежуток, на котором функция ![math]() непрерывна:
непрерывна:
 непрерывна:
непрерывна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие условия для непрерывной на отрезке ![math]() функции
функции ![math]() должны выполняться, чтобы
должны выполняться, чтобы ![math]() для некоторой точки
для некоторой точки ![math]() :
:
 функции
функции  должны выполняться, чтобы
должны выполняться, чтобы  для некоторой точки
для некоторой точки  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Тогда
. Тогда
 . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

4/5
Вычислить![math]()

4/3
Вычислить![math]()

1/5
Если ![math]() , то последовательность
, то последовательность ![math]()
 , то последовательность
, то последовательность 
(1) расходится
(2) сходится к ![math]()

(3) сходится к ![math]()

Вычислить![math]()

1
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
1
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Левой производной ![math]() функции
функции ![math]() в данной точке
в данной точке ![math]() называется
называется
 функции
функции  в данной точке
в данной точке  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть задана функция ![math]() . Отметьте верные утверждения:
. Отметьте верные утверждения:
 . Отметьте верные утверждения:
. Отметьте верные утверждения:
(1) функция определена на отрезке ![math]()

(2) является обратной для функции![math]() на
на ![math]()
 на
на 
(3) убывает в области определения
(4) производная равна![math]() на отрезке
на отрезке ![math]()
 на отрезке
на отрезке 
Если последовательность ![math]() такова, что интервал
такова, что интервал ![math]() при любом
при любом ![math]() содержит только конечное число членов последовательности, то ее предел
содержит только конечное число членов последовательности, то ее предел ![math]() равен
равен
 такова, что интервал
такова, что интервал  при любом
при любом  содержит только конечное число членов последовательности, то ее предел
содержит только конечное число членов последовательности, то ее предел  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Производная ![math]() -го порядка
-го порядка ![math]() разности двух функций
разности двух функций ![math]() равна
равна
 -го порядка
-го порядка  разности двух функций
разности двух функций  равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
2
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
2
Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0909
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0909
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какое условие теоремы Ролля не выполняется для функции ![math]() :
:
 :
:
(1) непрерывность на ![math]()

(2) дифференцируемость на ![math]()

(3) ![math]()

Пусть выполнены условия теоремы 5 (правило Лопиталя) для бесконечно больших функций ![math]() и
и ![math]() . Тогда предел
. Тогда предел ![math]()
 и
и  . Тогда предел
. Тогда предел 
(1) не существует
(2) равен ![math]()

(3) равен ![math]()

(4) равен нулю
(5) равен бесконечности
Каким свойством обладает многочлен Тейлора ![math]() функции
функции ![math]()
 функции
функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
2
Вычислить ![math]()

0
Решить уравнение ![math]()

(1) -1
(2) 1
(3) 4
(4) -4
(5) 2
(6) 3
(7) -3
(8) -2
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
0.125
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-0.125
Указать интервалы монотонности функции ![math]()

(1) возрастает на ![math]()

(2) возрастает на ![math]()

(3) убывает на ![math]() и возрастает на
и возрастает на ![math]()
 и возрастает на
и возрастает на 
(4) убывает на ![math]()

(5) возрастает на ![math]() и
и ![math]()
 и
и 
(6) убывает на ![math]() и
и ![math]()
 и
и 
Какие условия являются необходимыми, чтобы точка ![math]() была точкой перегиба кривой
была точкой перегиба кривой ![math]()
 была точкой перегиба кривой
была точкой перегиба кривой 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то ![math]() равно
равно
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое условие должно выполняться в точке ![math]() , чтобы при применении метода хорд точка пересечения хорды с осью
, чтобы при применении метода хорд точка пересечения хорды с осью ![math]() было приближением к корню уравнения
было приближением к корню уравнения ![math]() на отрезке
на отрезке ![math]() :
:
 , чтобы при применении метода хорд точка пересечения хорды с осью
, чтобы при применении метода хорд точка пересечения хорды с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
1
Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
0
Решить уравнение ![math]()

(1) -1
(2) 2
(3) -2
(4) 1
(5) 3
(6) -3
(7) 0
(8) 5
(9) -5
Найти точку перегиба функции ![math]() .
.
 .
.
-1
Найти точку перегиба функции ![math]() .
.
 .
.
-1
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Какое из заданных ниже соответствий является взаимно однозначным:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если ![math]() для
для ![math]() и
и ![math]() , то
, то ![math]()
 для
для  и
и  , то
, то 
(1) меньше или равен ![math]()

(2) больше или равен ![math]()

(3) равен ![math]()

(4) не обязательно существует
Какое свойство функции ![math]() является достаточным для того, чтобы функция
является достаточным для того, чтобы функция ![math]() являлась бесконечно малой при
являлась бесконечно малой при ![math]() (
(![math]() - б.м.ф. при
- б.м.ф. при ![math]() ):
):
 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):
(1) периодичность
(2) нечётность
(3) ограниченность
Множеством значений функции ![math]() является
является
 является
является
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

3
Даны две сходящиеся последовательности: ![math]() , причем
, причем ![math]() . Тогда предел последовательности
. Тогда предел последовательности ![math]()
 , причем
, причем  . Тогда предел последовательности
. Тогда предел последовательности 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

2
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какие из функций имеют равные правые и левые производные в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() бесконечно большая, то она
бесконечно большая, то она
 бесконечно большая, то она
бесконечно большая, то она
(1) ограничена снизу
(2) ограничена сверху
(3) ограничена
(4) неограниченна
Дифференциалом ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() называется
называется
 -го порядка
-го порядка  функции
функции  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть касательная к графику функции ![math]() , проведенная в точке
, проведенная в точке ![math]() параллельна прямой
параллельна прямой ![math]() . Найдите значение производной
. Найдите значение производной ![math]()
 , проведенная в точке
, проведенная в точке  параллельна прямой
параллельна прямой  . Найдите значение производной
. Найдите значение производной 
-4
Под каким углом пересекаются кривые ![math]() в точке
в точке ![math]()
 в точке
в точке 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0989
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.2
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Геометрический смысл теоремы Лагранжа состоит в том, что существует хотя бы одна точка графика функции ![math]() , в которой касательная
, в которой касательная
 , в которой касательная
, в которой касательная
(1) параллельна оси ![math]()

(2) перпендикулярна оси ![math]()

(3) параллельна хорде ![math]()

Какие утверждения справедливы:
(1) если ![math]() и
и ![math]() - бесконечно малые на бесконечности функции и существует предел
- бесконечно малые на бесконечности функции и существует предел ![math]() , то существует также предел
, то существует также предел ![math]() ;
;
 и
и  - бесконечно малые на бесконечности функции и существует предел
- бесконечно малые на бесконечности функции и существует предел  , то существует также предел
, то существует также предел  ;
;
(2) для бесконечно малых на бесконечности функций ![math]() и
и ![math]() , у которых и существует предел
, у которых и существует предел ![math]() , также существует предел
, также существует предел ![math]() ;
;
 и
и  , у которых и существует предел
, у которых и существует предел  , также существует предел
, также существует предел  ;
;
(3) если ![math]() и
и ![math]() - бесконечно большие на бесконечности функции и существует предел
- бесконечно большие на бесконечности функции и существует предел ![math]() , то существует также предел
, то существует также предел ![math]() ;
;
 и
и  - бесконечно большие на бесконечности функции и существует предел
- бесконечно большие на бесконечности функции и существует предел  , то существует также предел
, то существует также предел  ;
;
(4) для бесконечно больших на бесконечности функций ![math]() и
и ![math]() , у которых и существует предел
, у которых и существует предел ![math]() , также существует предел
, также существует предел ![math]() ;
;
 и
и  , у которых и существует предел
, у которых и существует предел  , также существует предел
, также существует предел  ;
; Какая из формул является выражением для остаточного члена ![math]() в форме Пеано:
в форме Пеано:
 в форме Пеано:
в форме Пеано:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
4
Вычислить ![math]()

-1
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) -1
(4) 3
(5) ![math]()

(6) ![math]()

(7) 0
(8) 1
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/64
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-7/24
Точка ![math]() называется точкой локального минимума функции
называется точкой локального минимума функции ![math]() , если
, если
 называется точкой локального минимума функции
называется точкой локального минимума функции  , если
, если
(1) ![math]()
![math]()


(2) ![math]()
![math]()


(3) ![math]()
![math]()


(4) ![math]()
![math]()


Какие условия являются достаточными, чтобы точка ![math]() была точкой перегиба кривой
была точкой перегиба кривой ![math]()
 была точкой перегиба кривой
была точкой перегиба кривой 
(1) при переходе через точку ![math]() знак
знак ![math]() не меняется
не меняется
 знак
знак  не меняется
не меняется
(2) при переходе через точку ![math]() знак
знак ![math]() постоянный
постоянный
 знак
знак  постоянный
постоянный
(3) при переходе через точку ![math]() знак
знак ![math]() меняется
меняется
 знак
знак  меняется
меняется Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то ![math]() равно
равно
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Второе приближение ![math]() корня уравнения
корня уравнения ![math]() на отрезке
на отрезке ![math]() методом касательных вычисляется по формуле:
методом касательных вычисляется по формуле:
 корня уравнения
корня уравнения  на отрезке
на отрезке  методом касательных вычисляется по формуле:
методом касательных вычисляется по формуле:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
3
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
-0.5
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
0.5
Найти точку перегиба функции ![math]() .
.
 .
.
-6
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/10
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Число ![math]() является
является
 является
является
(1) целым
(2) рациональным
(3) иррациональным
(4) натуральным
По определению, ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![math]() и
и ![math]() . Тогда (
. Тогда (![math]() - б.м.ф. при
- б.м.ф. при ![math]() ). Тогда предел функции
). Тогда предел функции ![math]()
 определена в некоторой окрестности точки
определена в некоторой окрестности точки  и
и  . Тогда (
. Тогда ( - б.м.ф. при
- б.м.ф. при  ). Тогда предел функции
). Тогда предел функции 
(1) не существует
(2) равен A
(3) не равен А
(4) больше А
Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() , то
, то
 непрерывна на отрезке
непрерывна на отрезке  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

-2
Вычислить![math]()

0
Вычислить![math]()

3
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

2
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() с помощью логарифмического дифференцирования вычисляется по формуле:
с помощью логарифмического дифференцирования вычисляется по формуле:
 с помощью логарифмического дифференцирования вычисляется по формуле:
с помощью логарифмического дифференцирования вычисляется по формуле:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется неубывающей, если
называется неубывающей, если ![math]()
 называется неубывающей, если
называется неубывающей, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана параметрически:
задана параметрически: ![math]() . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция ![math]() на интервале
на интервале ![math]() для того, чтобы существовала производная
для того, чтобы существовала производная ![math]() :
:
 задана параметрически:
задана параметрически:  . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция  на интервале
на интервале  для того, чтобы существовала производная
для того, чтобы существовала производная  :
:
(1) непрерывность
(2) дифференцируемость
(3) ограниченность
(4) монотонность
(5) периодичность
(6) существование обратной функции
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

1.01
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

1.9975
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какое выражение является формулой Коши для функций ![math]()
![math]() на отрезке [a,b]:
на отрезке [a,b]:

 на отрезке [a,b]:
на отрезке [a,b]:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какая их формул является разложением Маклорена для функции ![math]() c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
99
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
18
Для каких функций точка ![math]() является точкой локального максимума:
является точкой локального максимума:
 является точкой локального максимума:
является точкой локального максимума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для каких функций точка перегиба имеет абсциссу ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
0
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
1
Указать наименьший элемент множества ![math]()

-2
Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) -2
(4) 3
(5) 5
(6) 0
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вниз?
является выпуклой вниз?
 является выпуклой вниз?
является выпуклой вниз?
(1) 4
(2) 3
(3) 2
(4) 1
(5) 0
(6) -1
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Выражение ![math]() равно
равно
 равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какая из функций имеет предел на бесконечности, равный нулю:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть функции ![math]() определены в некоторой окрестности точки
определены в некоторой окрестности точки ![math]() и
и ![math]() . Тогда
. Тогда
 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и  . Тогда
. Тогда
(1) ![math]() , если
, если ![math]()
 , если
, если 
(2) ![math]() , если
, если ![math]()
 , если
, если 
(3) ![math]() , если
, если ![math]()
 , если
, если 
Отметьте верную формулу:
(1) ![math]()

(2) ![math]()

(3) ![math]()

На каком множестве должна быть непрерывна функция ![math]() для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
 для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
для того, чтобы она на этом множестве принимала свои наименьшее и наибольшее значения:
(1) на отрезке ![math]()

(2) на интервале ![math]()

(3) на полуинтервале ![math]()

(4) на полуинтервале ![math]()

Пусть ![math]() - бесконечно малые при
- бесконечно малые при ![math]() функции, причём
функции, причём ![math]() и
и ![math]() . Если
. Если ![math]() , то
, то
 - бесконечно малые при
- бесконечно малые при  функции, причём
функции, причём  и
и  . Если
. Если  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

-1/12
Вычислить![math]()

5/64
Вычислить![math]()

5/7
Вычислить![math]()

1
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
6
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
2
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Если касательная, проведённая к кривой ![math]() в точке
в точке ![math]() , параллельна оси Oy, то
, параллельна оси Oy, то ![math]()
 в точке
в точке  , параллельна оси Oy, то
, параллельна оси Oy, то 
(1) может равняться плюс бесконечности
(2) может равняться минус бесконечности
(3) равна конечному числу
Чему равна производная сложной функции ![math]() в точке
в точке ![math]() :
:
 в точке
в точке  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Приближённое значение функции ![math]() в точке
в точке ![math]() равно
равно
 в точке
в точке  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() ,
, ![math]() является
является
 ,
,  является
является
(1) возрастающей
(2) убывающей
(3) немонотонной
Постоянный вектор ![math]() не является пределом вектор-функции
не является пределом вектор-функции ![math]() при
при ![math]()
 не является пределом вектор-функции
не является пределом вектор-функции  при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.99
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.995
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какой должна быть функция ![math]() , чтобы теорема Лагранжа стала следствием теоремы Коши:
, чтобы теорема Лагранжа стала следствием теоремы Коши:
 , чтобы теорема Лагранжа стала следствием теоремы Коши:
, чтобы теорема Лагранжа стала следствием теоремы Коши:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
38
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
33
Какие из утверждений справедливы:
(1) если ![math]() , то функция
, то функция ![math]() имеет экстремум в точке
имеет экстремум в точке ![math]()
 , то функция
, то функция  имеет экстремум в точке
имеет экстремум в точке 
(2) если ![math]() - точка экстремума
- точка экстремума ![math]() , то
, то ![math]()
 - точка экстремума
- точка экстремума  , то
, то 
(3) если ![math]() - точка экстремума
- точка экстремума ![math]() , то
, то ![math]() - критическая точка
- критическая точка ![math]()
 - точка экстремума
- точка экстремума  , то
, то  - критическая точка
- критическая точка 
(4) если ![math]() - критическая точка
- критическая точка ![math]() , то
, то ![math]() - точка экстремума
- точка экстремума ![math]()
 - критическая точка
- критическая точка  , то
, то  - точка экстремума
- точка экстремума 
(5) если ![math]() или
или ![math]() - точка экстремума
- точка экстремума ![math]()
 или
или  - точка экстремума
- точка экстремума 
(6) если ![math]() или
или ![math]() - критическая точка
- критическая точка ![math]()
 или
или  - критическая точка
- критическая точка 
(7) если ![math]() - точка экстремума
- точка экстремума ![math]() , то
, то ![math]() или
или ![math]()
 - точка экстремума
- точка экстремума  , то
, то  или
или 
Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
2
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
-0.25
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) 0
(2) 2
(3) -2
(4) точек перегиба нет
(5) 1
(6) -1
Найти точку перегиба функции ![math]() .
.
 .
.
(1) -2
(2) 5
(3) -1
(4) точек перегиба нет
(5) 1
(6) 0
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Пусть ![math]() . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
 . Какие неравенства ему равносильны:
. Какие неравенства ему равносильны:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Отметьте верные утверждения
(1) определение непрерывности по Коши и по Гейне не эквивалентны
(2) если функция![math]() непрерывна в точке
непрерывна в точке ![math]() , то функции
, то функции ![math]() и
и![math]() непрерывны в этой точке
непрерывны в этой точке
 непрерывна в точке
непрерывна в точке  , то функции
, то функции  и
и непрерывны в этой точке
непрерывны в этой точке
(3) если функции![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]() , то функция
, то функция ![math]() непрерывна в этой точке
непрерывна в этой точке
 и
и  непрерывны в точке
непрерывны в точке  , то функция
, то функция  непрерывна в этой точке
непрерывна в этой точке Если ![math]() - б.м.ф. при
- б.м.ф. при ![math]() ,
, ![math]() и
и ![math]() , то
, то
 - б.м.ф. при
- б.м.ф. при  ,
,  и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

0
Вычислить![math]()

-2/3
Вычислить![math]()

-5/3
Вычислить![math]()

-8/15
Вычислить предел, используя асимптотические формулы ![math]()

25/9
Вычислить предел, используя асимптотические формулы ![math]()

3/10
Для каких из перечисленных функций ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Чему равна производная функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() убывает, то ее неограниченность означает, что
убывает, то ее неограниченность означает, что ![math]() равен
равен
 убывает, то ее неограниченность означает, что
убывает, то ее неограниченность означает, что  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна производная вектор-функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . Найдите силу тока в момент времени
. Найдите силу тока в момент времени ![math]() .
.
 , задается формулой
, задается формулой  . Найдите силу тока в момент времени
. Найдите силу тока в момент времени  .
.
25
Смещение груза на пружине описывается законом ![math]() . Найдите скорость
. Найдите скорость ![math]() тела в момент времени
тела в момент времени ![math]() .
.
 . Найдите скорость
. Найдите скорость  тела в момент времени
тела в момент времени  .
.
4
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.02
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.04
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) ![math]()

(6) -1
Вычислить предел ![math]()

1
Вычислить предел ![math]()

4
Для каких функций точка ![math]() является критической точкой:
является критической точкой:
 является критической точкой:
является критической точкой:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Прямая ![math]() является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции ![math]() , если
, если
 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]() или
или ![math]()
 или
или 
(4) ![math]()

С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 1
(3) 4
(4) -1
(5) 2
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 8
(2) точек перегиба нет
(3) 4
(4) -4
(5) 1
(6) 0
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
5
Для модуля ![math]() суммы двух чисел выбрать справедливое утверждение:
суммы двух чисел выбрать справедливое утверждение:
 суммы двух чисел выбрать справедливое утверждение:
суммы двух чисел выбрать справедливое утверждение:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Функция ![math]() при
при ![math]() , если
, если
 при
при  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

1
Вычислить![math]()

0
Вычислить предел, используя асимптотические формулы ![math]()

4
Вычислить предел, используя асимптотические формулы ![math]()

5/8
Если функция ![math]() дифференцируема в точке
дифференцируема в точке ![math]() , то она в этой точке
, то она в этой точке
 дифференцируема в точке
дифференцируема в точке  , то она в этой точке
, то она в этой точке
(1) имеет конечную производную ![math]()

(2) имеет бесконечную производную ![math]()

(3) непрерывна
(4) разрывна
Необходимое и достаточное условие сходимости последовательности ![math]() (критерий Коши ) формулируется следующим образом:
(критерий Коши ) формулируется следующим образом: ![math]()
 (критерий Коши ) формулируется следующим образом:
(критерий Коши ) формулируется следующим образом: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.005
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.005
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени  ?
?
4
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() ускорение точки было равным
ускорение точки было равным ![math]()
![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  ускорение точки было равным
ускорение точки было равным 
 ?
?
2
Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1)
![math]()

(2) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
5
При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
2
Пусть ![math]() - критическая точка
- критическая точка ![math]() , но
, но ![math]() непрерывна в
непрерывна в ![math]() . Тогда функция
. Тогда функция ![math]() в точке
в точке ![math]() имеет минимум, если её производная
имеет минимум, если её производная ![math]() при переходе через точку
при переходе через точку ![math]()
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет минимум, если её производная
имеет минимум, если её производная  при переходе через точку
при переходе через точку 
(1) меняет знак с минуса на плюс
(2) меняет знак с плюса на минус
(3) не меняет знак
Для функции ![math]() наклонные асимптоты при
наклонные асимптоты при ![math]() и
и ![math]()
 наклонные асимптоты при
наклонные асимптоты при  и
и 
(1) совпадают
(2) не совпадают
С помощью производной определите, какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

0
Найти точку перегиба функции ![math]()

0
Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Какое подмножество числовой прямой равносильно неравенству ![math]() :
:
 :
:
(1) отрезок ![math]()

(2) полуинтервал ![math]()

(3) полуинтервал ![math]()

(4) интервал ![math]()

Если функция ![math]() - бесконечно малая функция при
- бесконечно малая функция при ![math]() , то функция
, то функция ![math]()
 - бесконечно малая функция при
- бесконечно малая функция при  , то функция
, то функция 
(1) бесконечно большая
(2) бесконечно малая
(3) неограниченная
Как представить функцию ![math]() в виде композиции непрерывных функций
в виде композиции непрерывных функций ![math]() и
и ![math]()
 в виде композиции непрерывных функций
в виде композиции непрерывных функций  и
и 
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Что является асимптотической формулой для ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

3/2
Вычислить![math]()

0
Какие из перечисленных функций дифференцируемы в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если все частичные пределы последовательности одинаковы и равны ![math]() , то
, то
 , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.02
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.025
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Подобрать ![math]() так, чтобы при
так, чтобы при ![math]()
![math]()
 так, чтобы при
так, чтобы при 

2/3
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

0
Пусть в точке ![math]() функция
функция ![math]() имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
 функция
функция  имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
(1) если ![math]() и
и ![math]() , то
, то ![math]() - точка минимума для
- точка минимума для ![math]()
 и
и  , то
, то  - точка минимума для
- точка минимума для 
(2) если ![math]() и
и ![math]() , то
, то ![math]() - точка минимума для
- точка минимума для ![math]()
 и
и  , то
, то  - точка минимума для
- точка минимума для 
(3) если ![math]() - точка минимума для
- точка минимума для ![math]() , то
, то ![math]() и
и ![math]()
 - точка минимума для
- точка минимума для  , то
, то  и
и 
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Укажите точки разрыва функции ![math]()

(1) ![math]()

(2) точек разрыва нет
(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите наклонную асимптоту графика функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Какое из перечисленных ниже множеств является окрестностью точки ![math]()

(1) полуинтервал ![math]()

(2) интервал ![math]()

(3) интервал ![math]()

(4) интервал ![math]()

Число А называется пределом функции ![math]() справа
справа ![math]() , если
, если
 справа
справа  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

11/2
Вычислить![math]()

5/4
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) ![math]()

(4) -5
(5) 0
(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.515
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.4948
Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
4
Вычислить ![math]()

0
Отметить счетные множества
(1) 3Z - Множество целых чисел, кратных 3
(2) множество натуральных чисел, являющихся кубами ![math]()

(3) множество рациональных чисел Q
(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]()

(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/9
Какое из неравенств задаёт ![math]() -окрестность точки
-окрестность точки ![math]()
 -окрестность точки
-окрестность точки 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() , тогда
, тогда
 , тогда
, тогда
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

5/8
Вычислить![math]()

1/2
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать формулу Лагранжа для функции ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
2
Вычислить ![math]()

0
Найти точную верхнюю грань множества ![math]()

3
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 ; убывает на
; убывает на  и
и 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

8
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/2
Какое из перечисленных ниже множеств является множеством всех нижних граней для ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть функция ![math]() при
при![math]() и
и ![math]() при
при![math]()
 при
при и
и  при
при
(1) предел слева ![math]() равен 0
равен 0
 равен 0
равен 0
(2) предел справа ![math]() не равен пределу слева
не равен пределу слева ![math]()
 не равен пределу слева
не равен пределу слева 
(3) предел ![math]() существует
существует
 существует
существует Вычислить![math]()

9/98
Вычислить![math]()

7/8
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

1
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
(1) ![math]()

(2)
![math]()

Найти точную нижнюю грань множества ![math]()

-2
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Какое из перечисленных ниже множеств является ограниченным множеством:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

7
Вычислить![math]()

6/7
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
0
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
0
Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
2
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
-1
Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/2
Если ![math]() - точная нижняя грань множества
- точная нижняя грань множества ![math]() , то эта грань :
, то эта грань :
 - точная нижняя грань множества
- точная нижняя грань множества  , то эта грань :
, то эта грань :
(1) наименьшая нижняя
(2) наибольшая верхняя
(3) наименьшая верхняя
(4) наибольшая нижняя
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 4
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
9/2
Пусть задано множество ![math]() . Отметьте верные утверждения:
. Отметьте верные утверждения:
 . Отметьте верные утверждения:
. Отметьте верные утверждения:
(1) множество ![math]() счётно
счётно
 счётно
счётно
(2) множество всех нижних граней ![math]() пусто
пусто
 пусто
пусто
(3) точная верхняя грань множества ![math]() равна
равна![math]()
 равна
равна
(4) множество ![math]() ограничено
ограничено
 ограничено
ограничено Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/2
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
4
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/4
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
1275/101
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 2
(2) 3
(3) 6
(4) 4
(5) 9
(6) 12
Пусть ![math]() и
и ![math]() - множества натуральных, целых и рациональных чисел. Какая из записей верна:
- множества натуральных, целых и рациональных чисел. Какая из записей верна:
 и
и  - множества натуральных, целых и рациональных чисел. Какая из записей верна:
- множества натуральных, целых и рациональных чисел. Какая из записей верна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Указать область определения функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Функция ![math]() называется бесконечно малой функцией при
называется бесконечно малой функцией при ![math]() , стремящемся к
, стремящемся к ![math]() , если
, если ![math]()
 называется бесконечно малой функцией при
называется бесконечно малой функцией при  , стремящемся к
, стремящемся к  , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению ![math]() , функция
, функция ![math]() называется непрерывной в точке
называется непрерывной в точке ![math]() , если
, если ![math]()
 , функция
, функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если 
(1) равен ![math]()

(2) равен![math]()

(3) равен![math]()

(4) не существует
Для какого множества из непрерывности функции на нём следует её равномерная непрерывность:
(1) интервал ![math]()

(2) отрезок ![math]()

(3) полуинтервал ![math]()

(4) полуинтервал ![math]()

Вычислить![math]()

6
Вычислить![math]()

-6
Вычислить![math]()

5
Четвёртый член последовательности ![math]() равен
равен
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

1/5
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1/3
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]() если
если ![math]() и
и ![math]() , если
, если ![math]()
 - целая часть от
- целая часть от  .
.  если
если  и
и  , если
, если 
(1) да
(2) нет
Производной функции ![math]() в данной точке
в данной точке ![math]() называется
называется
 в данной точке
в данной точке  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие равенства верны:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() , где
, где ![math]()
 , где
, где 
Какая из перечисленных функций является обратной для функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется ограниченной, если
называется ограниченной, если ![math]()
 называется ограниченной, если
называется ограниченной, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() есть
есть
 -го порядка
-го порядка  функции
функции  есть
есть
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
10
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
5
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Каким условиям должны удовлетворять функции ![math]() и
и ![math]() в теореме Коши:
в теореме Коши:
 и
и  в теореме Коши:
в теореме Коши:
(1) непрерывность на ![math]()

(2) непрерывность на ![math]()

(3) ограниченность на ![math]()

(4) монотонность на ![math]()

(5) дифференцируемость на ![math]()

(6) дифференцируемость в точке ![math]()

(7) ![math]()

(8) ![math]()

(9) ![math]() на
на ![math]()
 на
на 
(10) ![math]() на
на ![math]()
 на
на 
Какую неопределённость нужно раскрыть при вычислении предела функции ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
2
Вычислить ![math]()

0
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
113/90
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-1
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-3
Функция ![math]() называется возрастающей на [a,b], если
называется возрастающей на [a,b], если ![math]()
 называется возрастающей на [a,b], если
называется возрастающей на [a,b], если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие утверждения справедливы:
(1) если ![math]() , то она принимает на нём наибольшее значение
, то она принимает на нём наибольшее значение
 , то она принимает на нём наибольшее значение
, то она принимает на нём наибольшее значение
(2) наибольшее значение ![math]() принимает только на концах отрезка
принимает только на концах отрезка
 принимает только на концах отрезка
принимает только на концах отрезка
(3) наибольшее значение ![math]() может принимать на концах отрезка
может принимать на концах отрезка
 может принимать на концах отрезка
может принимать на концах отрезка
(4) наибольшее значение ![math]() принимает только в точке локального максимума
принимает только в точке локального максимума
 принимает только в точке локального максимума
принимает только в точке локального максимума
(5) наибольшее значение ![math]() может принимать в точке локального максимума
может принимать в точке локального максимума
 может принимать в точке локального максимума
может принимать в точке локального максимума Если ![math]() и
и ![math]() , то прямая
, то прямая ![math]()
 и
и  , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Пусть для функции ![math]() в окрестности точки
в окрестности точки ![math]() существует производная
существует производная ![math]() -го порядка и
-го порядка и ![math]() - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда ![math]() - не является точкой минимума и максимума
- не является точкой минимума и максимума ![math]() , если
, если
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и  - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - не является точкой минимума и максимума
- не является точкой минимума и максимума  , если
, если
(1) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(2) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(3) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
(4) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
С помощью производной найти значение выражения ![math]() .
.
 .
.
0.5
С помощью производной найти значение выражения ![math]() .
.
 .
.
0.5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
4/33
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
1
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
-4
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
10
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
1/57
Пусть ![math]() (числа кратные 8-ми). Какое из перечисленных множеств есть множество
(числа кратные 8-ми). Какое из перечисленных множеств есть множество ![math]() :
:
 (числа кратные 8-ми). Какое из перечисленных множеств есть множество
(числа кратные 8-ми). Какое из перечисленных множеств есть множество  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению (Коши),![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая из перечисленных функций является б.б.ф. при ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие из перечисленных функций непрерывны в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Точка ![math]() называется точкой разрыва функции
называется точкой разрыва функции ![math]() второго рода , если в точке
второго рода , если в точке ![math]()
 называется точкой разрыва функции
называется точкой разрыва функции  второго рода , если в точке
второго рода , если в точке 
(1) конечные пределы слева и справа равны
(2) конечные пределы слева и справа не равны
(3) конечный предел слева или справа не существует
Пусть ![math]() б.м.ф. при
б.м.ф. при ![math]() и
и ![math]() . Тогда
. Тогда
 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

-1
Вычислить![math]()

2/3
Вычислить![math]()

1/9
Пусть ![math]() . Тогда, по определению предела,
. Тогда, по определению предела, ![math]()
 . Тогда, по определению предела,
. Тогда, по определению предела, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

2/3
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Производной функции![math]() является функция
является функция
 является функция
является функция
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если функции ![math]() дифференцируема, а
дифференцируема, а ![math]() не дифференцируема в точке
не дифференцируема в точке ![math]() , то их сумма
, то их сумма ![math]() в этой точке
в этой точке
 дифференцируема, а
дифференцируема, а  не дифференцируема в точке
не дифференцируема в точке  , то их сумма
, то их сумма  в этой точке
в этой точке
(1) дифференцируема
(2) не дифференцируема
Пусть функция ![math]() непрерывна и возрастает на
непрерывна и возрастает на ![math]() . Тогда обратная функция
. Тогда обратная функция ![math]() :
:
 непрерывна и возрастает на
непрерывна и возрастает на  . Тогда обратная функция
. Тогда обратная функция  :
:
(1) не определена в точке ![math]()

(2) непрерывна на отрезке, содержащем ![math]()

(3) возрастает и убывает на отрезке ![math]()

(4) возрастает на отрезке ![math]()

Последовательность ![math]() , где
, где ![math]() является
является
 , где
, где  является
является
(1) ограниченной
(2) неограниченной сверху
(3) неограниченной снизу
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
6
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Коши точка ![math]()

(1) совпадает с концами отрезка ![math]() или
или ![math]()
 или
или 
(2) лежит вне отрезка ![math]()

(3) принадлежит интервалу ![math]()

Пусть ![math]() и
и ![math]() - бесконечно малые на бесконечности функции, для которых существует предел
- бесконечно малые на бесконечности функции, для которых существует предел ![math]() . Тогда существует предел
. Тогда существует предел
 и
и  - бесконечно малые на бесконечности функции, для которых существует предел
- бесконечно малые на бесконечности функции, для которых существует предел  . Тогда существует предел
. Тогда существует предел
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 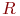 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-1
Пусть функция ![math]() непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную ![math]() на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
 непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
(1) ![math]() на
на ![math]() возрастает на [a,b]
возрастает на [a,b]
 на
на  возрастает на [a,b]
возрастает на [a,b]
(2) ![math]() на
на ![math]() возрастает на [a,b]
возрастает на [a,b]
 на
на  возрастает на [a,b]
возрастает на [a,b]
(3) ![math]() возрастает на
возрастает на ![math]() на
на ![math]()
 возрастает на
возрастает на  на
на 
(4) ![math]() возрастает на
возрастает на ![math]() на
на ![math]()
 возрастает на
возрастает на  на
на 
График дифференцируемой на интервале ![math]() функции
функции ![math]() не имеет на этом интервале выпуклость, направленную вверх или вниз, если график
не имеет на этом интервале выпуклость, направленную вверх или вниз, если график ![math]() лежит в пределах интервала
лежит в пределах интервала
 функции
функции  не имеет на этом интервале выпуклость, направленную вверх или вниз, если график
не имеет на этом интервале выпуклость, направленную вверх или вниз, если график  лежит в пределах интервала
лежит в пределах интервала
(1) не выше любой своей касательной
(2) не ниже любой своей касательной
(3) не выше и не ниже любой своей касательной
Для функции ![math]() точка (0,1) графика функции является
точка (0,1) графика функции является
 точка (0,1) графика функции является
точка (0,1) графика функции является
(1) точкой максимума
(2) точкой минимума
(3) точкой перегиба
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

(5) функция убывает на ![math]()

(6) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

(7) функция возрастает на ![math]()

(8) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 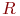 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наименьшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
4
Найти наименьшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
10
Укажите вертикальные асимптоты функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) нет
(6) ![math]()

Укажите точку максимума функции ![math]()

(1) -1
(2) 1
(3) 2
(4) 0
(5) -2
(6) нет
Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть ![math]() и
и ![math]() . Какое множество является пересечением
. Какое множество является пересечением ![math]()
 и
и  . Какое множество является пересечением
. Какое множество является пересечением 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() и
и ![math]() , то
, то
 и
и  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]() или
или ![math]()
 или
или 
Какое условие является достаточным для того, чтобы сумма двух функций ![math]() была бесконечно малой при при
была бесконечно малой при при ![math]() :
:
 была бесконечно малой при при
была бесконечно малой при при  :
:
(1) ![math]() - б.м.ф.,
- б.м.ф., ![math]() - б.м.ф.
- б.м.ф.
 - б.м.ф.,
- б.м.ф.,  - б.м.ф.
- б.м.ф.
(2) ![math]() - б.м.ф.,
- б.м.ф., ![math]() - ограниченная
- ограниченная
 - б.м.ф.,
- б.м.ф.,  - ограниченная
- ограниченная
(3) ![math]() ,
, ![math]() - б.м.ф.
- б.м.ф.
 ,
,  - б.м.ф.
- б.м.ф.
(4) ![math]() - б.м.ф.,
- б.м.ф., ![math]()
 - б.м.ф.,
- б.м.ф., 
Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() и
и ![math]() ,то
,то
 непрерывна в точке
непрерывна в точке  и
и  ,то
,то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Точка ![math]() для функции
для функции ![math]() является точкой разрыва
является точкой разрыва
 для функции
для функции  является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Вычислить![math]()

1/5
Вычислить![math]()

-1/7
Вычислить![math]()

1/3
Последовательность ![math]() является
является
 является
является
(1) сходящейся
(2) расходящейся
Вычислить![math]()

0
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
4
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
1/2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
1
Угловой коэффициент нормали, проведённой к кривой ![math]() в точке с абсциссой
в точке с абсциссой ![math]() , равен
, равен
 в точке с абсциссой
в точке с абсциссой  , равен
, равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для какого числа множеств выполняются правила дифференцирования их суммы:
(1) бесконечного
(2) конечного
Пусть функции ![math]() и
и ![math]() взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
 и
и  взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
(1) если производная ![math]() конечна и не равна нулю, то производная обратной функции в соответствующей точке тоже конечна
конечна и не равна нулю, то производная обратной функции в соответствующей точке тоже конечна
 конечна и не равна нулю, то производная обратной функции в соответствующей точке тоже конечна
конечна и не равна нулю, то производная обратной функции в соответствующей точке тоже конечна
(2) касательные взаимно обратных функций совпадают
(3) касательная к графику функции ![math]() в точке
в точке ![math]() является касательной к графику обратной функции, если она параллельна оси
является касательной к графику обратной функции, если она параллельна оси![math]()
 в точке
в точке  является касательной к графику обратной функции, если она параллельна оси
является касательной к графику обратной функции, если она параллельна оси
Запись ![math]() означает, что
означает, что ![math]()
 означает, что
означает, что 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна ![math]() -я производная функции
-я производная функции ![math]()
 -я производная функции
-я производная функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
2
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Найдите угловой коэффициент нормали к параболе ![math]() , перпендикулярной к прямой, соединяющей начало координат с вершиной параболы
, перпендикулярной к прямой, соединяющей начало координат с вершиной параболы
 , перпендикулярной к прямой, соединяющей начало координат с вершиной параболы
, перпендикулярной к прямой, соединяющей начало координат с вершиной параболы
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

К графику функции ![math]() в точке с абсциссой
в точке с абсциссой ![math]() проведена касательная. Найти абсциссу точки пересечения касательной и осью Ох
проведена касательная. Найти абсциссу точки пересечения касательной и осью Ох
 в точке с абсциссой
в точке с абсциссой  проведена касательная. Найти абсциссу точки пересечения касательной и осью Ох
проведена касательная. Найти абсциссу точки пересечения касательной и осью Ох Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В условиях теоремы Коши точка ![math]()

(1) совпадает с концами отрезка ![math]() или
или ![math]()
 или
или 
(2) лежит вне отрезка ![math]()

(3) принадлежит интервалу ![math]()

Каким условиям на бесконечности должны удовлетворять функции ![math]() и
и ![math]() , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
 и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
(1) ![math]() - бесконечно большая и
- бесконечно большая и ![math]() - бесконечно малая
- бесконечно малая
 - бесконечно большая и
- бесконечно большая и  - бесконечно малая
- бесконечно малая
(2) ![math]() - бесконечно малая и
- бесконечно малая и ![math]() -бесконечно большая
-бесконечно большая
 - бесконечно малая и
- бесконечно малая и  -бесконечно большая
-бесконечно большая
(3) ![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]()
 и
и  непрерывны в точке
непрерывны в точке 
(4) ![math]() и
и ![math]() дифференцируемы в окрестности точки
дифференцируемы в окрестности точки ![math]()
 и
и  дифференцируемы в окрестности точки
дифференцируемы в окрестности точки 
(5) существует ![math]()

(6) существует ![math]()

Верно ли, что функция ![math]() раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки ![math]()
 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 
(1) да
(2) нет
Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) -2
(6) 2
(7) -4
(8) 4
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
1/3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
1
Пусть функция ![math]() в точке
в точке ![math]() имеет производную
имеет производную ![math]() . Какое утверждение верно:
. Какое утверждение верно:
 в точке
в точке  имеет производную
имеет производную  . Какое утверждение верно:
. Какое утверждение верно:
(1) ![math]() убывает в точке
убывает в точке ![math]()
 убывает в точке
убывает в точке 
(2) ![math]() убывает в точке
убывает в точке ![math]()
 убывает в точке
убывает в точке 
(3) ![math]() убывает в точке
убывает в точке ![math]()
 убывает в точке
убывает в точке 
(4) ![math]() убывает в точке
убывает в точке ![math]()
 убывает в точке
убывает в точке 
Выпуклость кривой ![math]() в точке
в точке ![math]() направлена вверх, если
направлена вверх, если
 в точке
в точке  направлена вверх, если
направлена вверх, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для каких функций прямая ![math]() является вертикальной асимптотой:
является вертикальной асимптотой:
 является вертикальной асимптотой:
является вертикальной асимптотой:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Из предложенного списка выбрать те условия, которым должна удовлетворять функция ![math]() , чтобы уравнение
, чтобы уравнение ![math]() на отрезке
на отрезке ![math]() имело хотя бы одно решение:
имело хотя бы одно решение:
 , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке  имело хотя бы одно решение:
имело хотя бы одно решение:
(1) ![math]() непрерывна на
непрерывна на ![math]()
 непрерывна на
непрерывна на 
(2) ![math]() непрерывна на
непрерывна на ![math]()
 непрерывна на
непрерывна на 
(3) числа ![math]() и
и ![math]() одного знака
одного знака
 и
и  одного знака
одного знака
(4) числа ![math]() и
и ![math]() разных знаков
разных знаков
 и
и  разных знаков
разных знаков
(5) ![math]() одного знака на
одного знака на ![math]()
 одного знака на
одного знака на 
(6) ![math]() , меняющая знак на
, меняющая знак на ![math]()
 , меняющая знак на
, меняющая знак на 
(7) ![math]() одного знака на
одного знака на ![math]()
 одного знака на
одного знака на 
(8) ![math]() , меняющая знак на
, меняющая знак на ![math]()
 , меняющая знак на
, меняющая знак на 
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

(5) функция убывает на ![math]()

(6) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) 2
(6) -2
(7) 4
(8) -4
Из всех прямоугольников, вписанных в окружность радиуса 1, найти прямоугольник наибольшей площади. В ответе укажите его площадь.
2
Известно, что одно из двух чисел на 36 больше другого. Найдите эти числа, если известно, что их произведение принимает наименьшее значение. В ответе укажите большее из чисел.
18
Укажите вертикальные асимптоты функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) нет
(6) ![math]()

Укажите точку максимума функции ![math]()

(1) -1
(2) 1
(3) 2
(4) 0
(5) -2
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1000
Какое из предложенных числовых множеств является конечным:
(1) множество чётных чисел, меньших 7
(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая из функций является ограниченной в некоторой окрестности ![math]() , но не имеет конечного предела в этой точке:
, но не имеет конечного предела в этой точке:
 , но не имеет конечного предела в этой точке:
, но не имеет конечного предела в этой точке:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если ![math]() - б.м.ф. при
- б.м.ф. при ![math]() , а функция
, а функция ![math]() имеет конечный предел в точке
имеет конечный предел в точке ![math]() , то предел произведения
, то предел произведения ![math]()
 - б.м.ф. при
- б.м.ф. при  , а функция
, а функция  имеет конечный предел в точке
имеет конечный предел в точке  , то предел произведения
, то предел произведения 
(1) не существует
(2) равен нулю
(3) не равен нулю
(4) равен бесконечности
Указать числовой промежуток, на котором функция ![math]() непрерывна:
непрерывна:
 непрерывна:
непрерывна:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() . Сколько корней имеет данный многочлен:
. Сколько корней имеет данный многочлен:
 . Сколько корней имеет данный многочлен:
. Сколько корней имеет данный многочлен:
(1) один
(2) три
(3) хотя бы один
(4) ни одного
Пусть ![math]() . Тогда
. Тогда
 . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

-2
Вычислить![math]()

1/2
Вычислить![math]()

1/6
Вычислить![math]()

2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
3
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Если в точке ![math]() существует производная
существует производная ![math]() , то
, то
 существует производная
существует производная  , то
, то
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() является бесконечно малой, причем
является бесконечно малой, причем ![math]() , тогда
, тогда ![math]() равен
равен
 является бесконечно малой, причем
является бесконечно малой, причем  , тогда
, тогда  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Производная ![math]() -го порядка
-го порядка ![math]() произведения двух функций
произведения двух функций ![math]() равна
равна
 -го порядка
-го порядка  произведения двух функций
произведения двух функций  равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
25
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
1
Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1304
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1304
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какие числа могут быть точками ![math]() из теоремы Ролля для функции
из теоремы Ролля для функции ![math]()
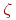 из теоремы Ролля для функции
из теоремы Ролля для функции 
(1) из интервала ![math]()

(2) из интервала ![math]()

(3) из интервала ![math]()

Пусть выполнены условия теоремы 6 (правило Лопиталя) для бесконечно больших функций ![math]() и
и ![math]() на бесконечности. Тогда предел
на бесконечности. Тогда предел ![math]()
 и
и  на бесконечности. Тогда предел
на бесконечности. Тогда предел 
(1) не существует
(2) равен ![math]()

(3) равен ![math]()

(4) равен нулю
(5) равен бесконечности
Как связаны многочлен Тейлора ![math]() функции
функции ![math]() , сама функция и остаточный член
, сама функция и остаточный член ![math]() :
:
 функции
функции  , сама функция и остаточный член
, сама функция и остаточный член  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решить уравнение ![math]()

(1) -1
(2) 1
(3) 3
(4) -3
(5) 2
(6) 0
(7) -2
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
3
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/27
Указать интервалы монотонности функции ![math]()

(1) возрастает на ![math]()

(2) возрастает на ![math]()

(3) убывает на ![math]() и возрастает на
и возрастает на ![math]()
 и возрастает на
и возрастает на 
(4) убывает на ![math]()

(5) возрастает на ![math]() и
и ![math]()
 и
и 
(6) убывает на ![math]() и
и ![math]()
 и
и 
Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то
(1) ![math]() или
или ![math]()
 или
или 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
0
Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
0.5
Решить уравнение ![math]()

(1) -2
(2) 1
(3) 2
(4) -1
(5) 3
(6) -3
Найти точку перегиба функции ![math]() .
.
 .
.
0.5
Найти точку перегиба функции ![math]() .
.
 .
.
1
Укажите вертикальные асимптоты функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Множество А называется счётным, если оно эквивалентно:
(1) множеству N натуральных чисел
(2) множеству Z целых чисел
(3) конечному множеству чисел
(4) множеству R действительных чисел
Какое свойство функции ![math]() является достаточным для того, чтобы функция
является достаточным для того, чтобы функция ![math]() являлась бесконечно малой при
являлась бесконечно малой при ![math]() (
(![math]() - б.м.ф. при
- б.м.ф. при ![math]() ):
):
 является достаточным для того, чтобы функция
является достаточным для того, чтобы функция  являлась бесконечно малой при
являлась бесконечно малой при  (
( - б.м.ф. при
- б.м.ф. при  ):
):
(1) периодичность
(2) нечётность
(3) ограниченность
Множеством значений функции ![math]() является
является
 является
является
(1) ![math]()

(2) ![math]()

(3) ![math]()

Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/2
Если ![math]() , то предел последовательности
, то предел последовательности ![math]()
 , то предел последовательности
, то предел последовательности 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

3
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какие из функций имеют равные правые и левые производные в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Дифференциал ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() можно вычислить по формуле
можно вычислить по формуле
 -го порядка
-го порядка  функции
функции  можно вычислить по формуле
можно вычислить по формуле
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти сумму ![math]() , где
, где ![math]() уравнение касательной к окружности
уравнение касательной к окружности ![math]() в точке
в точке ![math]()
 , где
, где  уравнение касательной к окружности
уравнение касательной к окружности  в точке
в точке 
-5
Под каким углами пересекаются кривые![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1503
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.3
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Остаточный член ![math]() для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
 для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
(1) в форме Пеано
(2) в форме Лагранжа
Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
2
Вычислить ![math]()

0
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) -2
(4) 4
(5) ![math]()

(6) ![math]()

(7) 2
(8) 0
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/12
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/64
Точка ![math]() не является точкой локального максимума функции
не является точкой локального максимума функции ![math]() , если
, если
 не является точкой локального максимума функции
не является точкой локального максимума функции  , если
, если
(1) ![math]()
![math]()


(2) ![math]()
![math]()


(3) ![math]()
![math]()


(4) ![math]()
![math]()


Если прямая ![math]() является наклонной асимптотой графика функции
является наклонной асимптотой графика функции ![math]() , то
, то
 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то
(1) ![math]() или
или ![math]()
 или
или 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Последовательности приближений корня уравнения ![math]() на отрезке
на отрезке ![math]() методом хорд и касательных являются
методом хорд и касательных являются
 на отрезке
на отрезке  методом хорд и касательных являются
методом хорд и касательных являются
(1) монотонными и неограниченными
(2) монотонными и ограниченными
(3) немонотонными и ограниченными
(4) немонотонными и неограниченными
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
1
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
-2
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
-3
Найти точку перегиба функции ![math]() .
.
 .
.
-7
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-9/7
Число ![math]() является
является
 является
является
(1) целым
(2) рациональным
(3) иррациональным
(4) натуральным
По определению, ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое условие является достаточным для ограниченности функции ![math]() на множестве
на множестве
 на множестве
на множестве
(1) непрерывность на отрезке ![math]()

(2) непрерывность на интервале ![math]()

(3) непрерывность на полуинтервале ![math]()

(4) непрерывность на полуинтервале ![math]()

Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/2
Вычислить![math]()

1/4
Вычислить![math]()

-1/3
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

2
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) нет
(2) да
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) нет
(2) да
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() задана параметрически:
задана параметрически: ![math]() . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция ![math]() на интервале
на интервале ![math]() для того, чтобы существовала производная
для того, чтобы существовала производная ![math]() :
:
 задана параметрически:
задана параметрически:  . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция  на интервале
на интервале  для того, чтобы существовала производная
для того, чтобы существовала производная  :
:
(1) непрерывность
(2) дифференцируемость
(3) ограниченность
(4) монотонность
(5) периодичность
(6) существование обратной функции
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.9933
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.5053
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какая их формул является разложением Маклорена для функции ![math]() c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
3
Вычислить ![math]()

0
Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
73
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
164
Для каких функций точка ![math]() является точкой локального минимума:
является точкой локального минимума:
 является точкой локального минимума:
является точкой локального минимума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Для каких функций точка перегиба имеет абсциссу ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
0
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
2
Указать наименьший элемент множества ![math]()

-1
Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) -2
(4) 3
(5) 1.5
(6) 0
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вверх?
является выпуклой вверх?
 является выпуклой вверх?
является выпуклой вверх?
(1) 2
(2) 1
(3) 0
(4) -1
(5) -2
(6) -3
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Выражение ![math]() равно
равно
 равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

Предел функции ![math]() на бесконечности
на бесконечности
 на бесконечности
на бесконечности
(1) не существует
(2) равен 1
(3) равен -1
(4) равен 0
Пусть функции ![math]() определены в некоторой окрестности точки
определены в некоторой окрестности точки ![math]() и
и ![math]() . Тогда
. Тогда
 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и  . Тогда
. Тогда
(1) ![math]() , если
, если ![math]() и
и ![math]()
 , если
, если  и
и 
(2) ![math]() , если
, если ![math]()
 , если
, если 
(3) ![math]()

Если функция ![math]() непрерывна на отрезке
непрерывна на отрезке ![math]() , то
, то
 непрерывна на отрезке
непрерывна на отрезке  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Какие условия должны выполняться, чтобы ![math]()

(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Вычислить![math]()

1/10
Вычислить![math]()

3
Вычислить![math]()

3/7
Вычислить![math]()

1/2
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
2
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
3
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

(6) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

По определению, функция ![math]() в точке
в точке ![math]() имеет бесконечную производную
имеет бесконечную производную ![math]() , если в этой точке
, если в этой точке
 в точке
в точке  имеет бесконечную производную
имеет бесконечную производную  , если в этой точке
, если в этой точке
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Каким условиям должны удовлетворять функции ![math]() в точках
в точках ![math]() и
и ![math]() соответственно , чтобы сложная функция
соответственно , чтобы сложная функция ![math]() была дифференцируемой в точке
была дифференцируемой в точке ![math]() :
:
 в точках
в точках  и
и  соответственно , чтобы сложная функция
соответственно , чтобы сложная функция  была дифференцируемой в точке
была дифференцируемой в точке  :
:
(1) ![math]() дифференцируема или
дифференцируема или ![math]() дифференцируема
дифференцируема
 дифференцируема или
дифференцируема или  дифференцируема
дифференцируема
(2) ![math]() непрерывна и
непрерывна и ![math]() дифференцируема
дифференцируема
 непрерывна и
непрерывна и  дифференцируема
дифференцируема
(3) ![math]() дифференцируема и
дифференцируема и ![math]() непрерывна
непрерывна
 дифференцируема и
дифференцируема и  непрерывна
непрерывна
(4) ![math]() дифференцируема и
дифференцируема и ![math]() дифференцируема
дифференцируема
 дифференцируема и
дифференцируема и  дифференцируема
дифференцируема Приближённое значение функции ![math]() в точке
в точке ![math]() равно
равно
 в точке
в точке  равно
равно
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() ,
, ![math]() является
является
 ,
,  является
является
(1) возрастающей
(2) убывающей
(3) немонотонной
Если постоянный вектор ![math]() является пределом вектор-функции
является пределом вектор-функции ![math]() , то
, то
 является пределом вектор-функции
является пределом вектор-функции  , то
, то
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.985
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
0.9925
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какие утверждения справедливы:
(1) теорема Коши следует из теоремы Лагранжа
(2) теорема Лагранжа следует из теоремы Коши
(3) теорема Ролля следует из теоремы Лагранжа
(4) теорема Лагранжа следует из теоремы Ролля
(5) теорема Коши следует из теоремы Ролля
(6) теорема Ролля следует из теоремы Коши
Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
20
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
316
Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
-1
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
2
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) -2
(2) 2
(3) -1
(4) точек перегиба нет
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) -1
(2) 2
(3) -2
(4) точек перегиба нет
(5) 1
(6) 0
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Пусть ![math]() . Какое неравенство ему равносильно?
. Какое неравенство ему равносильно?
 . Какое неравенство ему равносильно?
. Какое неравенство ему равносильно?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Отметьте верные утверждения
(1) определение непрерывности по Коши и по Гейне эквивалентны
(2) если функция![math]() непрерывна в точке
непрерывна в точке ![math]() , то функции
, то функции ![math]() и
и![math]() непрерывны в этой точке
непрерывны в этой точке
 непрерывна в точке
непрерывна в точке  , то функции
, то функции  и
и непрерывны в этой точке
непрерывны в этой точке
(3) если функции![math]() и
и ![math]() непрерывны в точке
непрерывны в точке ![math]() , то функции
, то функции ![math]() непрерывна в этой точке
непрерывна в этой точке
 и
и  непрерывны в точке
непрерывны в точке  , то функции
, то функции  непрерывна в этой точке
непрерывна в этой точке Если ![math]() и
и ![math]() - б.м.ф. при
- б.м.ф. при ![math]() . Какое условие необходимо и достаточно для того, чтобы
. Какое условие необходимо и достаточно для того, чтобы ![math]()
 и
и  - б.м.ф. при
- б.м.ф. при  . Какое условие необходимо и достаточно для того, чтобы
. Какое условие необходимо и достаточно для того, чтобы 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

0
Вычислить![math]()

0
Вычислить![math]()

16
Вычислить![math]()

1/2
Вычислить предел, используя асимптотические формулы ![math]()

1/3
Вычислить предел, используя асимптотические формулы ![math]()

1/4
Для каких из перечисленных функций ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Чему равна производная функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() возрастает и ее точная верхняя грань
возрастает и ее точная верхняя грань ![math]() , то предел последовательности
, то предел последовательности ![math]() равен
равен
 возрастает и ее точная верхняя грань
возрастает и ее точная верхняя грань  , то предел последовательности
, то предел последовательности  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . В какой момент времени сила тока равна
. В какой момент времени сила тока равна ![math]() ?
?
 , задается формулой
, задается формулой  . В какой момент времени сила тока равна
. В какой момент времени сила тока равна  ?
?
1
Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . Найдите силу тока в момент времени
. Найдите силу тока в момент времени ![math]() .
.
 , задается формулой
, задается формулой  . Найдите силу тока в момент времени
. Найдите силу тока в момент времени  .
.
5
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.03
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.06
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
2
Вычислить ![math]()

0
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) -2
(3) 0
(4) ![math]()

(5) ![math]()

(6) -1
Вычислить предел ![math]()

2
Вычислить предел ![math]()

-2
Для каких функций точка ![math]() является точкой экстремума:
является точкой экстремума:
 является точкой экстремума:
является точкой экстремума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) 3
(4) -2
(5) 1.5
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 10
(2) точек перегиба нет
(3) 4
(4) 5
(5) 1
(6) 0
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-12/7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3
Для модуля ![math]() разности двух чисел выбрать справедливое утверждение:
разности двух чисел выбрать справедливое утверждение:
 разности двух чисел выбрать справедливое утверждение:
разности двух чисел выбрать справедливое утверждение:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() , а функция
, а функция ![math]() непрерывна в точке
непрерывна в точке ![math]() , то сложная функция
, то сложная функция ![math]()
 непрерывна в точке
непрерывна в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке  , то сложная функция
, то сложная функция 
(1) разрывна в точке ![math]()

(2) непрерывна в точке ![math]()

(3) ![math]()

Что является асимптотической формулой для ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

-3/2
Вычислить![math]()

5/2
Вычислить предел, используя асимптотические формулы ![math]()

2
Вычислить предел, используя асимптотические формулы ![math]()

-2
Какое условие эквивалентно дифференцируемости функции ![math]() в точке
в точке ![math]() :
:
 в точке
в точке  :
:
(1) существование конечной производной ![math]()

(2) существование бесконечной производной ![math]()

(3) непрерывность в точке ![math]()

(4) разрывность в точке ![math]()

Последовательность ![math]() монотонно возрастает, а
монотонно возрастает, а ![math]() убывает, причем
убывает, причем ![math]() и
и ![math]() . Тогда по принципу вложенных отрезков
. Тогда по принципу вложенных отрезков
 монотонно возрастает, а
монотонно возрастает, а  убывает, причем
убывает, причем  и
и  . Тогда по принципу вложенных отрезков
. Тогда по принципу вложенных отрезков
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0075
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0075
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени  ?
?
(1) ![math]()
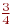
(2)
![math]()
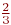
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() скорость точки была равна
скорость точки была равна ![math]() м/с?
м/с?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  скорость точки была равна
скорость точки была равна  м/с?
м/с?
1
Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]()

0
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
2
Найти ![math]() :
: ![math]()
 :
: 
-1/3
Пусть ![math]() - критическая точка
- критическая точка ![math]() , но
, но ![math]() непрерывна в
непрерывна в ![math]() . Тогда функция
. Тогда функция ![math]() в точке
в точке ![math]() имеет экстремум, если её производная
имеет экстремум, если её производная ![math]() при переходе через точку
при переходе через точку ![math]()
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет экстремум, если её производная
имеет экстремум, если её производная  при переходе через точку
при переходе через точку 
(1) меняет знак с минуса на плюс
(2) меняет знак с плюса на минус
(3) не меняет знак
Для функции ![math]() наклонные асимптоты при
наклонные асимптоты при ![math]() и
и ![math]()
 наклонные асимптоты при
наклонные асимптоты при  и
и 
(1) совпадают
(2) не совпадают
С помощью производной определите,какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

0
Найти точку перегиба функции ![math]()

0
Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) x=0
Укажите точку максимума функции ![math]()

(1) 0.5
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
-6
Какое подмножество числовой прямой равносильно неравенству ![math]() :
:
 :
:
(1) отрезок ![math]()

(2) полуинтервал ![math]()

(3) полуинтервал ![math]()

(4) интервал ![math]()

Если функция ![math]() - бесконечно большая функция при
- бесконечно большая функция при ![math]() , то предел функции
, то предел функции ![math]() равен
равен
 - бесконечно большая функция при
- бесконечно большая функция при  , то предел функции
, то предел функции  равен
равен
(1) ![math]()

(2) 0
(3) ![math]()

Как представить функцию ![math]() в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций ![math]() и
и ![math]()
 в виде композиции двух непрерывных функций
в виде композиции двух непрерывных функций  и
и 
(1) ![math]() и
и ![math]()
 и
и 
(2) ![math]() и
и ![math]()
 и
и 
(3) ![math]() и
и ![math]()
 и
и 
(4) ![math]() и
и ![math]()
 и
и 
Что является асимптотической формулой для ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

0
Вычислить![math]()

3/4
Какие из перечисленных функций дифференцируемы в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Последовательность ![math]() , у которой существуют хотя бы два различных частичных предела
, у которой существуют хотя бы два различных частичных предела ![math]() и
и ![math]() ,
, ![math]()
 , у которой существуют хотя бы два различных частичных предела
, у которой существуют хотя бы два различных частичных предела  и
и  ,
, 
(1) сходится к ![math]()

(2) сходится к ![math]()

(3) сходится к ![math]()

(4) расходится
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.03
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
2.0375
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
2
Вычислить ![math]()

0
Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Подобрать ![math]() так, чтобы при
так, чтобы при ![math]()
![math]()
 так, чтобы при
так, чтобы при 

4/3
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

2
Пусть в точке ![math]() функция
функция ![math]() имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка ![math]() была точкой максимума для
была точкой максимума для ![math]() :
:
 функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой максимума для
была точкой максимума для  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Укажите вертикальные асимптоты функции![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Укажите точку максимума функции ![math]()

(1) -0.25
(2) 1
(3) 2
(4) ![math]()

(5) 0
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Какое из перечисленных ниже множеств является окрестностью точки ![math]()

(1) полуинтервал ![math]()

(2) интервал ![math]()

(3) полуинтервал ![math]()

(4) интервал ![math]()

Предел справа ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

-2/5
Вычислить![math]()

3/5
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.5225
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.4927
Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]()

0
Отметить счетные множества
(1) 4Z - Множество целых чисел, кратных 4
(2) множество натуральных чисел, являющихся 4-ми степенями ![math]()

(3) множество рациональных чисел Q
(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 ; убывает на
; убывает на  и
и 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/6
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Какое из неравенств задаёт ![math]() -окрестность точки
-окрестность точки ![math]()
 -окрестность точки
-окрестность точки 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какое условие является критерием существования предела функции в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/6
Вычислить![math]()

8
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Определить количество корней уравнения ![math]() на всей числовой оси
на всей числовой оси
 на всей числовой оси
на всей числовой оси
1
Вычислить ![math]()

0
Найти точную верхнюю грань множества ![math]()

4
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

-1
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/6
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-7/2
Какое из перечисленных ниже множеств является множеством всех верхних граней для ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть функция ![math]() ,
, ![math]()
 ,
, 
(1) предел слева ![math]() равен 0
равен 0
 равен 0
равен 0
(2) предел справа ![math]() не равен пределу слева
не равен пределу слева ![math]()
 не равен пределу слева
не равен пределу слева 
(3) предел ![math]() существует
существует
 существует
существует Вычислить![math]()

1/8
Вычислить![math]()

-2
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

2
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
(1) ![math]()

(2)
![math]()

Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти точную нижнюю грань множества ![math]()

-5
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Какие из перечисленных ниже множеств являются ограниченными снизу множествами:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

1/4
Вычислить![math]()

0
Вычислить предел данной последовательности: ![math]()

(1) 1
(2) 2
(3) 0
(4) ![math]()

(5) -5
(6) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
-2
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
(1) ![math]()

(2)
![math]()

Найти точную верхнюю грань множества ![math]()

1/3
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
2
Найти точную верхнюю грань множества ![math]()

1/3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
5/2
Какое условие является достаточным для существования точной верхней грани множества:
(1) неограниченность снизу
(2) ограниченность сверху
(3) неограниченность сверху
(4) ограниченность снизу
Вычислить![math]()

0
Вычислить![math]()

0
Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 5
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2/3
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
(1) ![math]()

(2)
![math]()

Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
4
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
149
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
100/301
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 5
(2) 6
(3) 30
(4) 4
(5) 8
(6) 12
Число ![math]() является
является
 является
является
(1) целым
(2) рациональным
(3) иррациональным
(4) натуральным
Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

3/2
Вычислить![math]()

-3/2
Вычислить![math]()

1/2
 равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

1/12
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.99
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.504
Найти ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
20
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
909
Для каких функций точка ![math]() является точкой локального максимума:
является точкой локального максимума:
 является точкой локального максимума:
является точкой локального максимума:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
0
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
1
Указать наименьший элемент множества ![math]()

-2
Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) -2
(4) 3
(5) 5
(6) 0
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вниз?
является выпуклой вниз?
 является выпуклой вниз?
является выпуклой вниз?
(1) 0
(2) 1
(3) 2
(4) 3
(5) 4
(6) 5
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Какое условие является достаточным для существования точной нижней грани множества:
(1) неограниченность снизу
(2) ограниченность сверху
(3) неограниченность сверху
(4) ограниченность снизу
Вычислить![math]()

0
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 6
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
11/10
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/8
Указать область определения функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

По определению (Гейне), функция ![math]() называется непрерывной в точке
называется непрерывной в точке ![math]() , если
, если ![math]() , соответствующая
, соответствующая ![math]()
 называется непрерывной в точке
называется непрерывной в точке  , если
, если  , соответствующая
, соответствующая 
(1) сходится к ![math]()

(2) сходится к ![math]()

(3) сходится к ![math]()

(4) расходится
Какая из указанных функций является равномерно непрерывной на интервале ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить![math]()

-7
Вычислить![math]()

2
Вычислить![math]()

1
Вычислить![math]()

7
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Производной функции ![math]() в данной точке
в данной точке ![math]() называется
называется
 в данной точке
в данной точке  называется
называется
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Последовательность ![math]() называется неограниченной, если
называется неограниченной, если ![math]()
 называется неограниченной, если
называется неограниченной, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
11
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Какую неопределённость нужно раскрыть при вычислении предела функции ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
2
Вычислить ![math]()

0
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
193/90
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-1
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-3
Функция ![math]() называется неубывающей на [a,b], если
называется неубывающей на [a,b], если ![math]()
 называется неубывающей на [a,b], если
называется неубывающей на [a,b], если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какие утверждения справедливы:
(1) если ![math]() , то она принимает на наименьшее значение
, то она принимает на наименьшее значение
 , то она принимает на наименьшее значение
, то она принимает на наименьшее значение
(2) наименьшее значение ![math]() принимает только на концах отрезка
принимает только на концах отрезка
 принимает только на концах отрезка
принимает только на концах отрезка
(3) наименьшее значение ![math]() может принимать на концах отрезка
может принимать на концах отрезка
 может принимать на концах отрезка
может принимать на концах отрезка
(4) наименьшее значение ![math]() принимает только в точке локального минимума
принимает только в точке локального минимума
 принимает только в точке локального минимума
принимает только в точке локального минимума
(5) наименьшее значение ![math]() может принимать в точке локального минимума
может принимать в точке локального минимума
 может принимать в точке локального минимума
может принимать в точке локального минимума Если ![math]() или
или ![math]() , то прямая
, то прямая ![math]()
 или
или  , то прямая
, то прямая 
(1) может не быть асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
Пусть для функции ![math]() в окрестности точки
в окрестности точки ![math]() существует производная
существует производная ![math]() -го порядка и
-го порядка и ![math]() - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда ![math]() является точкой перегиба графика функции, если
является точкой перегиба графика функции, если
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и  - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  является точкой перегиба графика функции, если
является точкой перегиба графика функции, если
(1) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(2) ![math]() -четное и
-четное и ![math]()
 -четное и
-четное и 
(3) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
(4) ![math]() -нечетное и
-нечетное и ![math]()
 -нечетное и
-нечетное и 
С помощью производной найти значение выражения ![math]() .
.
 .
.
-0.5
С помощью производной найти значение выражения ![math]() .
.
 .
.
1.5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
19/99
Найти наибольшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
0
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
3
Отметьте верные утверждения для функции ![math]()

(1) функция четная;
(2) функция непериодическая;
(3) функция нечетная;
(4) график функции симметричен относительно оси ординат
(5) функция периодическая;
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
45
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
9/19
По определению (Коши),![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Какая из перечисленных функций является б.б.ф. при ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Пусть ![math]() б.м.ф. при
б.м.ф. при ![math]() и
и ![math]() . Тогда
. Тогда
 б.м.ф. при
б.м.ф. при  и
и  . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]() более высокого порядка, чем
более высокого порядка, чем ![math]()
 более высокого порядка, чем
более высокого порядка, чем 
(3) ![math]() более высокого порядка, чем
более высокого порядка, чем ![math]()
 более высокого порядка, чем
более высокого порядка, чем 
(4) ![math]() эквивалентны
эквивалентны
 эквивалентны
эквивалентны
(5) не сравнимы
Вычислить![math]()

-3
Вычислить![math]()

5/7
Вычислить![math]()

6
Пусть число ![math]() - предел последовательности
- предел последовательности ![math]() . Тогда
. Тогда ![math]() вне окрестности
вне окрестности ![math]() лежит
лежит
 - предел последовательности
- предел последовательности  . Тогда
. Тогда  вне окрестности
вне окрестности  лежит
лежит
(1) бесконечное число элементов ![math]()

(2) конечное число элементов ![math]()

Вычислить![math]()

3/7
Определить порядок малости m бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3/2
Определить порядок малости m бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3/2
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Производной функции![math]() является функция
является функция
 является функция
является функция
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если функции ![math]() дифференцируема в точке
дифференцируема в точке ![math]() и
и ![math]() , а
, а ![math]() не дифференцируема в точке
не дифференцируема в точке ![math]() , то их произведение
, то их произведение ![math]() в этой точке
в этой точке
 дифференцируема в точке
дифференцируема в точке  и
и  , а
, а  не дифференцируема в точке
не дифференцируема в точке  , то их произведение
, то их произведение  в этой точке
в этой точке
(1) дифференцируемо
(2) не дифференцируемо
Пусть функция ![math]() непрерывна и убывает на
непрерывна и убывает на![math]() . Тогда обратная функция
. Тогда обратная функция ![math]() :
:
 непрерывна и убывает на
непрерывна и убывает на . Тогда обратная функция
. Тогда обратная функция  :
:
(1) не определена в точке ![math]()

(2) непрерывна на отрезке ![math]()

(3) возрастает или убывает на отрезке ![math]()

(4) ![math]()

Последовательность ![math]() , где
, где ![math]() является
является
 , где
, где  является
является
(1) ограниченной
(2) ограниченной сверху
(3) неограниченной
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
24
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
26
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() . найти дифференциал
. найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  . найти дифференциал
. найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть ![math]() и
и ![math]() - бесконечно большие на бесконечности функции, для которых существует предел
- бесконечно большие на бесконечности функции, для которых существует предел ![math]() . Тогда существует предел
. Тогда существует предел
 и
и  - бесконечно большие на бесконечности функции, для которых существует предел
- бесконечно большие на бесконечности функции, для которых существует предел  . Тогда существует предел
. Тогда существует предел
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
3
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 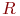 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-3
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-2
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 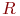 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-4
Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-10
Отметьте верные утверждения для функции ![math]() :
:
 :
:
(1) функция четная
(2) функция непериодическая
(3) график функции симметричен относительно оси ординат
(4) функция нечетная
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) нет
(2) 0
(3) 1
(4) 2
(5) -1
(6) -2
Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте верные утверждения:
(1) каждая ограниченная функция имеет предел в точке
(2) функция не может иметь в точке два разных предела
(3) определение предела по Коши и по Гейне эквивалентны
Если ![math]() - б.м.ф. при
- б.м.ф. при ![math]() , а функция
, а функция ![math]() имеет в точке
имеет в точке ![math]() конечный предел, отличный от нуля, то предел частного
конечный предел, отличный от нуля, то предел частного ![math]()
 - б.м.ф. при
- б.м.ф. при  , а функция
, а функция  имеет в точке
имеет в точке  конечный предел, отличный от нуля, то предел частного
конечный предел, отличный от нуля, то предел частного 
(1) не существует
(2) равен нулю
(3) не равен нулю
(4) равен бесконечности
Пусть ![math]() . Тогда
. Тогда
 . Тогда
. Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) не сравнимы
Вычислить![math]()

-1
Вычислить![math]()

3/4
Вычислить![math]()

5/7
Вычислить![math]()

3/5
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Если в точке ![math]() существует производная
существует производная ![math]() , то
, то
 существует производная
существует производная  , то
, то
(1) не существует![math]()

(2) производная в этой точке равна![math]()

(3) производная в этой точке не равна![math]() или
или![math]()
 или
или
Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если последовательность ![math]() является бесконечно малой, а
является бесконечно малой, а ![math]() - ограниченной (
- ограниченной (![math]() ) , то
) , то ![math]() равен
равен
 является бесконечно малой, а
является бесконечно малой, а  - ограниченной (
- ограниченной ( ) , то
) , то  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Пусть ![math]() взаимно обратные функции. Тогда производная
взаимно обратные функции. Тогда производная ![math]() -го порядка
-го порядка ![math]() равна
равна
 взаимно обратные функции. Тогда производная
взаимно обратные функции. Тогда производная  -го порядка
-го порядка  равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
16
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
1
Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0526
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0526
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Решить уравнение ![math]()

(1) -1
(2) -7
(3) 7
(4) 1
(5) 6
(6) 2
(7) -2
(8) -6
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
3
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-0.125
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
4
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
-0.25
Решить уравнение ![math]()

(1) -3
(2) 3
(3) 1
(4) -1
(5) 2
(6) -2
(7) 6
(8) -6
Найти точку перегиба функции ![math]() .
.
 .
.
0.5
Найти точку перегиба функции ![math]() .
.
 .
.
2
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) ![math]()

(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
- 6/7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
4
Предел функции ![math]() на бесконечности
на бесконечности
 на бесконечности
на бесконечности
(1) не существует
(2) равен 1
(3) равен -1
(4) равен 0
Пусть функции ![math]() определены в некоторой окрестности точки
определены в некоторой окрестности точки ![math]() и
и ![math]() ,. Тогда
,. Тогда
 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и  ,. Тогда
,. Тогда
(1) ![math]()

(2) ![math]() , если
, если ![math]()
 , если
, если 
(3) ![math]() , если
, если ![math]()
 , если
, если 
Вычислить![math]()

-2
Вычислить![math]()

7
Вычислить![math]()

3/2
Вычислить![math]()

5/11
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
3
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
3
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

По определению, функция ![math]() в точке
в точке ![math]() имеет бесконечную производную
имеет бесконечную производную ![math]() , если в этой точке
, если в этой точке
 в точке
в точке  имеет бесконечную производную
имеет бесконечную производную  , если в этой точке
, если в этой точке
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вектор-функция ![math]() называется непрерывной при
называется непрерывной при ![math]() , если
, если
 называется непрерывной при
называется непрерывной при  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.005
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.0025
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
19
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
909
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
-3
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
2.5
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) -2
(2) 2
(3) -1
(4) точек перегиба нет
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 1
(2) 2
(3) -2
(4) точек перегиба нет
(5) -1
(6) 0
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/3
Если функция ![math]() - бесконечно малая функция при
- бесконечно малая функция при ![math]() , то предел функции
, то предел функции ![math]() равен
равен
 - бесконечно малая функция при
- бесконечно малая функция при  , то предел функции
, то предел функции  равен
равен
(1) ![math]()

(2) 0
(3) ![math]()

Функция ![math]() является непрерывной в силу теоремы
является непрерывной в силу теоремы
 является непрерывной в силу теоремы
является непрерывной в силу теоремы
(1) о непрерывности сложной функции
(2) о непрерывности суммы и произведения функций
(3) о сохранении знака функции
Вычислить![math]()

1/2
Вычислить![math]()

0
Какие из перечисленных функций непрерывны, но не дифференцируемы в точке ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.99
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9875
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

2
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

0.5
Пусть в точке ![math]() функция
функция ![math]() имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка ![math]() была точкой минимума для
была точкой минимума для ![math]() :
:
 функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой минимума для
была точкой минимума для  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Предел слева ![math]() , если
, если
 , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

7/8
Вычислить![math]()

28
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала: . Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала: . Округлите значение до 4 знаков после запятой. ![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала: . Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала: . Округлите значение до 4 знаков после запятой.  ,
, 
0.4925
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.5031
Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
3
Вычислить ![math]()

0
Отметить счетные множества
(1) 5Z - Множество целых чисел, кратных 5
(2) множество натуральных чисел, являющихся 5-ми степенями ![math]()

(3) множество рациональных чисел Q
(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/12
Если функция ![math]() непрерывна в точке
непрерывна в точке ![math]() и
и ![math]() ,то
,то ![math]()
 непрерывна в точке
непрерывна в точке  и
и  ,то
,то 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Точка ![math]() для функции
для функции ![math]() является точкой разрыва
является точкой разрыва
 для функции
для функции  является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Пусть ![math]() б.м.ф. при
б.м.ф. при ![math]() и
и ![math]() .Тогда
.Тогда
 б.м.ф. при
б.м.ф. при  и
и  .Тогда
.Тогда
(1) ![math]() одного порядка
одного порядка
 одного порядка
одного порядка
(2) ![math]() более высокого порядка, чем
более высокого порядка, чем ![math]()
 более высокого порядка, чем
более высокого порядка, чем 
(3) ![math]() более высокого порядка, чем
более высокого порядка, чем ![math]()
 более высокого порядка, чем
более высокого порядка, чем 
(4) ![math]() эквивалентны
эквивалентны
 эквивалентны
эквивалентны
(5) не сравнимы
Вычислить![math]()

4
Вычислить![math]()

-1/9
Вычислить![math]()

1
Вычислить![math]()

4
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
1
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
1
Какое из перечисленных уравнений является уравнением касательной к кривой ![math]() в точке с абсциссой
в точке с абсциссой ![math]() :
:
 в точке с абсциссой
в точке с абсциссой  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Для какого числа функций выполняются правила дифференцирования их произведения:
(1) бесконечного
(2) конечного
По определению, запись ![math]() означает, что
означает, что ![math]()
 означает, что
означает, что 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Чему равна ![math]() -я производная функции
-я производная функции ![math]()
 -я производная функции
-я производная функции 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
(1) ![math]()

(2)
![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1/2
К графику функции ![math]() в точке с абсциссой
в точке с абсциссой ![math]() проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 19
проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 19
 в точке с абсциссой
в точке с абсциссой  проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 19
проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 19
19.5
Дана функция ![math]() . Найти угол (в градусах), который образует касательная к данной кривой в точке
. Найти угол (в градусах), который образует касательная к данной кривой в точке ![math]() с положительным направлением оси Ох
с положительным направлением оси Ох
 . Найти угол (в градусах), который образует касательная к данной кривой в точке
. Найти угол (в градусах), который образует касательная к данной кривой в точке  с положительным направлением оси Ох
с положительным направлением оси Ох
135
Для функции ![math]() ,
, ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Каким условиям в точке ![math]() должны удовлетворять функции
должны удовлетворять функции ![math]() и
и ![math]() , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
 должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
(1) ![math]() - бесконечно малая и - бесконечно малая
- бесконечно малая и - бесконечно малая
 - бесконечно малая и - бесконечно малая
- бесконечно малая и - бесконечно малая
(2) ![math]() - бесконечно большая и - бесконечно малая
- бесконечно большая и - бесконечно малая
 - бесконечно большая и - бесконечно малая
- бесконечно большая и - бесконечно малая
(3) ![math]() - бесконечно малая и - бесконечно большая
- бесконечно малая и - бесконечно большая
 - бесконечно малая и - бесконечно большая
- бесконечно малая и - бесконечно большая
(4) ![math]() и
и ![math]() непрерывны
непрерывны
 и
и  непрерывны
непрерывны
(5) ![math]() и
и ![math]() дифференцируемы для достаточно больших
дифференцируемы для достаточно больших ![math]()
 и
и  дифференцируемы для достаточно больших
дифференцируемы для достаточно больших 
(6) существует ![math]()

(7) существует ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) -3
(6) 3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
8/3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-11/24
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) 3
(6) -3
Из всех прямоугольников, вписанных в окружность радиуса ?2, найти прямоугольник наибольшей площади. В ответе укажите максимальную длину его стороны.
2
Известно, что одно из двух чисел меньше другого на 28. Найдите эти числа, если известно, что их произведение принимает наименьшее значение. В ответе укажите меньшее из чисел.
-14
Отметьте верные утверждения для функции ![math]() :
:
 :
:
(1) функция четная
(2) функция непериодическая
(3) график функции симметричен относительно оси ординат
(4) функция нечетная
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) нет
(2) ![math]()

(3) 1
(4) 0.75
(5) -1
(6) -2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Чему эквивалентна функция ![math]() при
при ![math]()
 при
при 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

2
Если ![math]() , то последовательность
, то последовательность ![math]()
 , то последовательность
, то последовательность 
(1) расходится
(2) сходится к ![math]()

(3) сходится к ![math]()

Вычислить![math]()

1/2
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Производная функции ![math]() равна
равна
 равна
равна
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Дифференциал ![math]() -го порядка
-го порядка ![math]() функции
функции ![math]() можно вычислить по формуле
можно вычислить по формуле
 -го порядка
-го порядка  функции
функции  можно вычислить по формуле
можно вычислить по формуле
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

К графику функции ![math]() в точке с абсциссой
в точке с абсциссой ![math]() проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 29
проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 29
 в точке с абсциссой
в точке с абсциссой  проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 29
проведена касательная. Найти абсциссу той точки касательной, ордината которой равна 29
10
Определить угол между левой и правой касательными к кривой ![math]() в точке
в точке ![math]()
 в точке
в точке 
90
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.0494
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1001
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Остаточный член ![math]() для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
 для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
(1) в форме Пеано
(2) в форме Лагранжа
(3) в форме Коши
Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
(1) ![math]()

(2)
![math]()

Вычислить ![math]()

0
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 1
(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) 2
(8) 0
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/64
Точка ![math]() не является точкой локального минимума функции
не является точкой локального минимума функции ![math]() , если
, если
 не является точкой локального минимума функции
не является точкой локального минимума функции  , если
, если
(1) ![math]()
![math]()


(2) ![math]()
![math]()


(3) ![math]()
![math]()


(4) ![math]()
![math]()


Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
0.5
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
7
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
-1.5
Найти точку перегиба функции ![math]() .
.
 .
.
2
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

0
Вычислить![math]()

0
Вычислить![math]()

-27
Вычислить![math]()

-1/2
Вычислить предел, используя асимптотические формулы ![math]()

2
Вычислить предел, используя асимптотические формулы ![math]()

1/2
Для каких из перечисленных функций ![math]() :
:
 :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Если последовательность ![math]() убывает и ее точная нижняя грань
убывает и ее точная нижняя грань ![math]() то предел последовательности
то предел последовательности ![math]()
 убывает и ее точная нижняя грань
убывает и ее точная нижняя грань  то предел последовательности
то предел последовательности 
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . Найдите силу тока в момент времени
. Найдите силу тока в момент времени ![math]() .
.
 , задается формулой
, задается формулой  . Найдите силу тока в момент времени
. Найдите силу тока в момент времени  .
.
3
Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . Найдите силу тока в момент времени
. Найдите силу тока в момент времени ![math]() .
.
 , задается формулой
, задается формулой  . Найдите силу тока в момент времени
. Найдите силу тока в момент времени  .
.
38
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.01
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.02
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
3
Вычислить ![math]()

-1
Отметьте значения, принадлежащие данному множеству ![math]()

(1) -1
(2) 2
(3) 0
(4) ![math]()

(5) ![math]()

(6) 1
Вычислить предел ![math]()

-10
Вычислить предел ![math]()

-6
Для каких функций точка ![math]() является критической точкой:
является критической точкой:
 является критической точкой:
является критической точкой:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) точек перегиба нет
(2) 2
(3) 4
(4) -2
(5) -1.5
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 12
(2) точек перегиба нет
(3) 4
(4) 6
(5) 1
(6) 0
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) 0.5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

2
Вычислить![math]()

3/2
Вычислить предел, используя асимптотические формулы ![math]()

3/2
Вычислить предел, используя асимптотические формулы ![math]()

2
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9975
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9975
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени  ?
?
(1) ![math]()
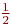
(2)
![math]()
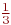
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() ускорение точки было равным
ускорение точки было равным ![math]()
![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  ускорение точки было равным
ускорение точки было равным 
 ?
?
0
Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
7
Вычислить ![math]()

0
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
0.5
Найти ![math]() :
: ![math]()
 :
: 
4/3
С помощью производной определите, какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

(1) точек перегиба нет
(2) 1
(3) -2
(4) 3
(5) 0
(6) 4
Найти точку перегиба функции ![math]()

0
Отметьте верные утверждения для функции ![math]()

(1) функция четная
(2) функция непериодическая
(3) функция нечетная
(4) график функции симметричен относительно оси ординат
(5) функция периодическая
(6) график функции симметричен относительно начала координат
Укажите точку минимума функции ![math]()

(1) 2
(2) 0
(3) 1
(4) нет
(5) ![math]()

(6) -3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
12
Вычислить![math]()

2/3
Вычислить![math]()

1/5
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать формулу Коши для функций ![math]() и
и ![math]() на отрезке
на отрезке ![math]() и найти соответствующее значение
и найти соответствующее значение ![math]() . В качестве ответа ввести значение
. В качестве ответа ввести значение ![math]()
 и
и  на отрезке
на отрезке  и найти соответствующее значение
и найти соответствующее значение  . В качестве ответа ввести значение
. В качестве ответа ввести значение 
2
Вычислить ![math]()

2
Найти точную верхнюю грань множества ![math]()

2
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]()

(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

0
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/2
Вычислить![math]()

1/2
Вычислить![math]()

0
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

1
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
4
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти точную нижнюю грань множества ![math]()

-7
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

5/8
Вычислить![math]()

1/16
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
-1
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
54
Найти точную верхнюю грань множества ![math]()

1/2
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
1
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
-1
Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-3/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
5/2
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-2
Найти ![math]() для функции
для функции ![math]()
![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции 
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
1
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
1
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Установить, чему равняется![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]() . Ответ укажите в виде несократимой дроби, например - 2/3.
. Ответ укажите в виде несократимой дроби, например - 2/3.
 и вычислить значение этого выражения при
и вычислить значение этого выражения при  . Ответ укажите в виде несократимой дроби, например - 2/3.
. Ответ укажите в виде несократимой дроби, например - 2/3.
100/201
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 3
(2) 2
(3) 6
(4) 9
(5) 12
(6) 5
По определению (Коши),![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

-3/2
Вычислить![math]()

-5/2
Вычислить![math]()

4
Вычислить![math]()

1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
3
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

1
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
4
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
3
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 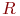 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-3
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-3
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

(7) функция возрастает на ![math]()

(8) функция убывает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

(7) функция возрастает на ![math]()

(8) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 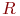 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наименьшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
6
Найти наименьшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
12
Укажите абсциссу точки пересечения графика функции с осью OX ![math]()

(1) 2
(2) нет
(3) -2
(4) 1
(5) -1
(6) 0
Укажите при каких значениях аргумента (из перечисленных) функция ![math]() является возрастающей
является возрастающей
 является возрастающей
является возрастающей
(1) -2
(2) -0.5
(3) 0.5
(4) 2
(5) 3
(6) 4
Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Точка ![math]() для функции
для функции ![math]() является точкой разрыва
является точкой разрыва
 для функции
для функции  является точкой разрыва
является точкой разрыва
(1) устранимой
(2) с конечным скачком
(3) второго рода
Б.м.ф. ![math]() при
при ![math]() имеет порядок малости
имеет порядок малости ![math]() , если
, если
 при
при  имеет порядок малости
имеет порядок малости  , если
, если
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/9
Вычислить![math]()

1/4
Вычислить![math]()

4
Вычислить![math]()

1/4
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
1/2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
1/2
Какое из перечисленных уравнений является уравнением нормали к кривой ![math]() в точке с абсциссой
в точке с абсциссой ![math]() :
:
 в точке с абсциссой
в точке с абсциссой  :
:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
-1
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
8
К графику функции ![math]() в точке с абсциссой
в точке с абсциссой ![math]() проведена касательная. Найти острый угол между касательной и осью
проведена касательная. Найти острый угол между касательной и осью
 в точке с абсциссой
в точке с абсциссой  проведена касательная. Найти острый угол между касательной и осью
проведена касательная. Найти острый угол между касательной и осью
30
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]()

0
Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) -6
(6) 0
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
4
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
-11/24
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) 6
(6) 0
Сумма двух целых чисел равна 24. Найдите эти числа, если известно, что их произведение принимает наибольшее значение. В ответе укажите большее из чисел.
12
Представьте число 3 в виде суммы двух положительных слагаемых так, чтобы сумма утроенного первого слагаемого и куба второго слагаемого была наименьшей. В ответе укажите большее из чисел.
2
Укажите абсциссу точки пересечения графика функции с осью OX ![math]()

(1) ![math]()

(2) нет
(3) -1.5
(4) 1
(5) -1
(6) 0
Укажите при каких значениях аргумента (из перечисленных) функция ![math]() является возрастающей
является возрастающей
 является возрастающей
является возрастающей
(1) -2
(2) -0.5
(3) 1.5
(4) 2
(5) 3
(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

10
Вычислить![math]()

5
Вычислить![math]()

1/3
Вычислить![math]()

8
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1/3
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
6
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
2
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 ,
,  найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

0
Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
34/9
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-1
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-3
С помощью производной найти значение выражения ![math]() .
.
 .
.
0.5
С помощью производной найти значение выражения ![math]() .
.
 .
.
-2.5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
8/9
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
5
Найти наибольшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
9
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
1/20
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
2/3
Вычислить![math]()

-2/3
Вычислить![math]()

-6
Вычислить![math]()

1/9
Вычислить![math]()

0
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
3
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
1
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Если ![math]() , то в точке
, то в точке ![math]() производная
производная ![math]()
 , то в точке
, то в точке  производная
производная 
(1) существует и равна ![math]()

(2) не существует
(3) существует и равна ![math]()

(4) существует и не равна ![math]()

(5) существует и не равна ![math]()

Если последовательность ![math]() является бесконечно большой, причем
является бесконечно большой, причем ![math]() . Тогда
. Тогда ![math]() равен
равен
 является бесконечно большой, причем
является бесконечно большой, причем  . Тогда
. Тогда  равен
равен
(1) ![math]()

(2) ![math]()

(3) ![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
8
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
2
Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1111
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1111
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

Решить уравнение ![math]()

(1) -2
(2) 2
(3) 3
(4) -3
(5) 1
(6) -1
(7) 0
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1
Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
0
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
1
Решить уравнение ![math]()

(1) -3
(2) 3
(3) -1
(4) 1
(5) 4
(6) -4
(7) 6
(8) -6
Найти точку перегиба функции ![math]() .
.
 .
.
-1
Найти точку перегиба функции ![math]() .
.
 .
.
-2
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/5
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

-5
Вычислить![math]()

10
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) да
(2) нет
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ординату точки кривой ![math]() касательная в которой параллельна оси Ох.
касательная в которой параллельна оси Ох.
 касательная в которой параллельна оси Ох.
касательная в которой параллельна оси Ох.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Определить угол между левой и правой касательными к кривой ![math]() в точке
в точке ![math]()
 в точке
в точке 
90
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1007
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1998
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

63
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 1
(4) 0
(5) ![math]()

(6) ![math]()

(7) -1
(8) 3
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/6
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/24
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
-3
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
1
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
5
Найти точку перегиба функции ![math]() .
.
 .
.
1
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

3
Вычислить![math]()

1/4
Вычислить![math]()

-1/12
Вычислить![math]()

0
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) да
(2) нет
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

2.0008
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.4933
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
515
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
1234
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
2
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
2
Указать наименьший элемент множества ![math]()

-3
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вверх?
является выпуклой вверх?
 является выпуклой вверх?
является выпуклой вверх?
(1) 1
(2) 2
(3) 3
(4) 4
(5) 5
(6) 6
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вверх?
является выпуклой вверх?
 является выпуклой вверх?
является выпуклой вверх?
(1) -2
(2) -1
(3) 0
(4) 1
(5) 2
(6) 3
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

-3
Вычислить![math]()

-3
Вычислить![math]()

-1/4
Вычислить![math]()

-1/3
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
2
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
4
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.01
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.005
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
35
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
215
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
6
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
5
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) 2
(2) -2
(3) -1
(4) точек перегиба нет
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) -0.5
(2) 2
(3) 4
(4) точек перегиба нет
(5) 1
(6) 0
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]()

1/4
Вычислить![math]()

1/5
Вычислить![math]()

5
Вычислить![math]()

-20
Вычислить предел, используя асимптотические формулы ![math]()

5/2
Вычислить предел, используя асимптотические формулы ![math]()

1/2
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . В какой момент времени сила тока равна
. В какой момент времени сила тока равна ![math]() ?
?
 , задается формулой
, задается формулой  . В какой момент времени сила тока равна
. В какой момент времени сила тока равна  ?
?
1
Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . В какой момент времени сила тока равна
. В какой момент времени сила тока равна ![math]() ?
?
 , задается формулой
, задается формулой  . В какой момент времени сила тока равна
. В какой момент времени сила тока равна  ?
?
2
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.02
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.04
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить ![math]()

-12
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) -1
(2) -3
(3) 0
(4) ![math]()

(5) ![math]()

(6) 1
Вычислить предел ![math]()

2
Вычислить предел ![math]()

-2
Если ![math]() , то прямая
, то прямая ![math]()
 , то прямая
, то прямая 
(1) не является асимптотой
(2) является наклонной асимптотой
(3) является горизонтальной асимптотой
(4) является вертикальной асимптотой
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) 2
(2) точек перегиба нет
(3) 4
(4) -2
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 14
(2) точек перегиба нет
(3) -7
(4) 7
(5) 1
(6) 0
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

-3/2
Вычислить предел, используя асимптотические формулы ![math]()

(1) ln 8/ln 2
(2) ln 6/ln 3
(3) ln 10/ln 2
(4) ln 12/ln 6
Вычислить предел, используя асимптотические формулы ![math]()

1/2
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 3 знаков после запятой.
. Округлите значение до 3 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 3 знаков после запятой.
. Округлите значение до 3 знаков после запятой.
1,995
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.995
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени
— время в секундах, измеренное с начала движения. Чему равно ускорение движения в момент времени  ?
?
2
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() скорость точки была равна
скорость точки была равна ![math]() м/с?
м/с?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  скорость точки была равна
скорость точки была равна  м/с?
м/с?
0
Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
7
Найти ![math]()

1
С помощью производной определите, какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

0
Найти точку перегиба функции ![math]()

(1) 1
(2) точек перегиба нет
(3) -2
(4) 3
(5) 0
(6) 4
Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) ![math]()

(5) ![math]()

(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
7
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Вычислить![math]()

10/11
Вычислить![math]()

12
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.98
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.975
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

3
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

0.125
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Укажите абсциссу точки пересечения графика функции ![math]() с осью OX
с осью OX
 с осью OX
с осью OX
(1) 2
(2) нет
(3) -2
(4) 1
(5) -1
(6) 0
Укажите точки перегиба функции ![math]()

(1) ![math]()

(2) ![math]()

(3) нет
(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

-15/2
Вычислить![math]()

1/3
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.485
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.5052
Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Вычислить ![math]()

0
Отметить счетные множества
(1) 6Z - Множество целых чисел, кратных 6
(2) множество натуральных чисел, являющихся 6-ми степенями ![math]()

(3) множество положительных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]()

(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 и
и  ; убывает на
; убывает на  и
и 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 ; убывает на
; убывает на  и
и 
(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() Варианты ответа:
Варианты ответа:
 Варианты ответа:
Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/9
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/9
Вычислить![math]()

2/5
Вычислить![math]()

5/9
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Вычислить ![math]()

0
Найти точную верхнюю грань множества ![math]()

3
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]()
 и
и  ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

-1
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Вычислить![math]()

1/3
Вычислить![math]()

1
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
-36
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

-4
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

-1/2
Вычислить![math]()

-10/11
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
0
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
(1) ![math]()

(2)
![math]()

Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
3
Найти точную верхнюю грань множества ![math]()

2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]()

1/2
Вычислить![math]()

1/7
Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 7
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
8/11
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/9
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-3
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
(1) ![math]()

(2) ![math]()

Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
1
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
100/401
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 4
(2) 37
(3) 148
(4) 3
(5) 6
(6) 9
Вычислить![math]()

-5
Вычислить![math]()

26
Вычислить![math]()

1
Вычислить![math]()

9
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Является ли следующая функция непрерывной в каждой точке своей области определения? Примечание: ![math]() - целая часть от
- целая часть от ![math]() .
. ![math]()
 - целая часть от
- целая часть от  .
. 
(1) да
(2) нет
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
0
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
1
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Написать уравнение касательной и нормали к параболе ![math]() в точке с абсциссой
в точке с абсциссой ![math]() .
.
 в точке с абсциссой
в точке с абсциссой  .
.
(1) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(2) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(3) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(4) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
(5) Касательная: ![math]() ; Нормаль:
; Нормаль: ![math]()
 ; Нормаль:
; Нормаль: 
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]() ,
, ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически:  ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]() \
\
 \
\ Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
163/90
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-2
Разложить по степеням ![math]() функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: ![math]()
 функцию, указать коэффициент при квадрате:
функцию, указать коэффициент при квадрате: 
-3
С помощью производной найти значение выражения ![math]() .
.
 .
.
3
С помощью производной найти значение выражения ![math]() .
.
 .
.
2
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
8/33
Найти наибольшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
4
Найти наименьшее значение функции ![math]() на отрезке
на отрезке ![math]() .
.
 на отрезке
на отрезке  .
.
-2
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -1
(2) 1
(3) 0
(4) -2
(5) 2
(6) нет
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
1/56
Записать пятый член последовательности ![math]() , если
, если ![math]()
 , если
, если 
3/5
Вычислить![math]()

-1
Вычислить![math]()

5/4
Вычислить![math]()

1/2
Вычислить![math]()

2/3
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
4
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2/3
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Определить какого рода точка разрыва у следующей функции. В качестве ответа введите число 1 или 2. ![math]()

2
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
4
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
6
Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти длину отрезка ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() ,
, ![math]()
 ,
, 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить ![math]()

0
Вычислить ![math]()

1
Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 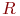 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-3
Разложить по степеням ![math]() функцию
функцию ![math]() указать коэффициент при квадрате:
указать коэффициент при квадрате:
 функцию
функцию  указать коэффициент при квадрате:
указать коэффициент при квадрате:
-2
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция возрастает на ![math]()

(2) функция убывает на ![math]()

(3) функция возрастает на ![math]()

(4) функция убывает на ![math]()

(5) функция возрастает на ![math]()

(6) функция убывает на ![math]()

Даны числовые множества: ![math]() – множество натуральных чисел,
– множество натуральных чисел, ![math]() – множество целых чисел,
– множество целых чисел, ![math]() – множество рациональных чисел,
– множество рациональных чисел, ![math]() – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
 – множество натуральных чисел,
– множество натуральных чисел,  – множество целых чисел,
– множество целых чисел,  – множество рациональных чисел,
– множество рациональных чисел, 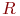 – множество действительных чисел. Тогда справедливо высказывание, что ...
– множество действительных чисел. Тогда справедливо высказывание, что ...
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-6
Найти наибольшее значение функции ![math]() при
при ![math]() .
.
 при
при  .
.
-12
Укажите ординату точки пересечения графика функции с осью OY ![math]()

(1) 2
(2) нет
(3) -1
(4) ![math]()

(5) -2
(6) 0
Укажите при каких значениях аргумента (из перечисленных) функция ![math]() является выпуклой вверх
является выпуклой вверх
 является выпуклой вверх
является выпуклой вверх
(1) -2
(2) 0.9
(3) 0
(4) -3
(5) 2
(6) 3
Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Записать формулу общего члена последовательности ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить![math]()

7
Вычислить![math]()

7/9
Вычислить![math]()

1/3
Вычислить![math]()

1
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
2
Определить порядок малости ![math]() бесконечно малой функции
бесконечно малой функции ![math]() относительно бесконечно малой функции
относительно бесконечно малой функции ![math]() при
при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 бесконечно малой функции
бесконечно малой функции  относительно бесконечно малой функции
относительно бесконечно малой функции  при
при  .
.  ,
,  ,
, 
1
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0).
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение f(0). 
1/2
Доопределить функцию ![math]() в точке
в точке ![math]() так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение ![math]() .
. ![math]()
 в точке
в точке  так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение
так, чтобы получившаяся функция была непрерывна. В качестве ответа введите значение  .
. 
0
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
3
Вычислить значение производной функции ![math]() в точке
в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 в точке
в точке  , пользуясь определением производной.
, пользуясь определением производной.
-2
Найдите коэффициент ![math]() уравнения
уравнения ![math]() касательной к графику функции
касательной к графику функции ![math]() , которая параллельная прямой
, которая параллельная прямой ![math]()
 уравнения
уравнения  касательной к графику функции
касательной к графику функции  , которая параллельная прямой
, которая параллельная прямой 
5
Найти свободный член уравнения касательной, записанной в виде ![math]() с угловым коэффициентом, которая параллельна данной прямой
с угловым коэффициентом, которая параллельна данной прямой ![math]() .
.
 с угловым коэффициентом, которая параллельна данной прямой
с угловым коэффициентом, которая параллельна данной прямой  .
.
-1
Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти дифференциал
найти дифференциал ![math]() . Выберите верный ответ.
. Выберите верный ответ.
 найти дифференциал
найти дифференциал  . Выберите верный ответ.
. Выберите верный ответ.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную от следующей вектор-функции: ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]()

0
Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при
, указать коэффициент при ![math]() :
: ![math]()
 функцию
функцию  , указать коэффициент при
, указать коэффициент при  :
: 
1/6
Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

Найти интервалы монотонности функции ![math]()
![math]() .
.

 .
.
(1) функция убывает на ![math]()

(2) функция возрастает на ![math]()

(3) функция убывает на ![math]()

(4) функция возрастает на ![math]()

(5) функция убывает на ![math]()

(6) функция возрастает на ![math]()

Отметьте значения, удовлетворяющие данному равенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Произведение двух положительных чисел равно 484. Найдите эти числа, если известно, что их сумма принимает наибольшее значение. В ответе укажите меньшее из чисел.
22
Представьте число 5 в виде суммы двух положительных слагаемых так, чтобы произведение первого слагаемого и куба второго слагаемого было наибольшим. В ответе укажите меньшее из чисел.
1.25
Укажите ординату точки пересечения графика функции с осью OY ![math]()

(1) 2
(2) нет
(3) -1
(4) ![math]()

(5) -2
(6) 0
Укажите при каких значениях аргумента (из перечисленных) функция ![math]() является выпуклой вверх
является выпуклой вверх
 является выпуклой вверх
является выпуклой вверх
(1) -2
(2) 1
(3) 0
(4) -1
(5) 2
(6) 3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
100
Вычислить![math]()

-1/2
Вычислить![math]()

6/5
Вычислить![math]()

2/3
Вычислить![math]()

2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
2
Определить порядок малости ![math]() для разности двух функций
для разности двух функций ![math]() относительно
относительно ![math]() при
при ![math]() .
. ![math]() ,
, ![math]()
 для разности двух функций
для разности двух функций  относительно
относительно  при
при  .
.  ,
, 
1/2
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Пользуясь теоремой Больцано-Коши, выяснить, обращается ли следующая функция в ноль на заданном отрезке? ![math]() ,
, ![math]()
 ,
, 
(1) да
(2) нет
Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
(1) ![math]()

(2)
![math]()

Вычислить значение производной функции в точке ![math]() , пользуясь определением производной.
, пользуясь определением производной.
 , пользуясь определением производной.
, пользуясь определением производной.
3
Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти угол пересечения между двумя линиями ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1765
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1765
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

1
Решить уравнение ![math]()

(1) -2
(2) 2
(3) 4
(4) -4
(5) 1
(6) -1
(7) -3
(8) 3
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/27
Разложить по ф. Тейлора до ![math]() в окрестности
в окрестности ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 в окрестности
в окрестности  функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-6
Найти точку локального минимума функции ![math]()
![math]() .
.

 .
.
-0.5
Найти точку локального максимума функции ![math]()
![math]() .
.

 .
.
-2
Решить уравнение ![math]()

(1) -3
(2) 3
(3) 2
(4) -2
(5) 1
(6) -1
(7) 7
(8) -7
Найти точку перегиба функции ![math]() .
.
 .
.
1
Найти точки перегиба функции ![math]() . В ответе укажите меньшую из них.
. В ответе укажите меньшую из них.
 . В ответе укажите меньшую из них.
. В ответе укажите меньшую из них.
0
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -0.1
(2) 0.1
(3) 0.9
(4) -2
(5) 2
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1/9
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

3
Вычислить![math]()

2
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Являются ли бесконечно малые величины ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

Решите неравенство методом интервалов, пользуясь свойством непрерывности функции. Укажите все правильные интервалы. ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти произведение координат точек кривой ![math]() ,в которых касательная параллельна биссектрисе первого координатного угла
,в которых касательная параллельна биссектрисе первого координатного угла
 ,в которых касательная параллельна биссектрисе первого координатного угла
,в которых касательная параллельна биссектрисе первого координатного угла
0
Дана кривая ![math]() . Найти произведение угловых коэффициентов нормали и касательной в точке
. Найти произведение угловых коэффициентов нормали и касательной в точке ![math]()
 . Найти произведение угловых коэффициентов нормали и касательной в точке
. Найти произведение угловых коэффициентов нормали и касательной в точке 
-4
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.1496
Для функции ![math]() вычислите дифференциал
вычислите дифференциал ![math]() и приращение функции
и приращение функции ![math]() в заданной точке
в заданной точке ![math]() при приращении аргумента
при приращении аргумента ![math]() . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой: ![math]() ,
, ![math]() ,
, ![math]()
 вычислите дифференциал
вычислите дифференциал  и приращение функции
и приращение функции  в заданной точке
в заданной точке  при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
,  ,
, 
0.2998
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

1
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 2
(4) 0
(5) ![math]()

(6) ![math]()

(7) -2
(8) 4
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
1/6
Разложить по ф. Маклорена до ![math]() функцию
функцию ![math]() , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: ![math]()
 функцию
функцию  , указать коэффициент при старшей степени:
, указать коэффициент при старшей степени: 
-1/24
Найти значение функции ![math]()
![math]() в точке локального минимума.
в точке локального минимума.

 в точке локального минимума.
в точке локального минимума.
-1
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
1.25
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
-3
Найти точку перегиба функции ![math]() .
.
 .
.
-4
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -4
(2) 4
(3) 0
(4) -2
(5) 2
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-5
Вычислить![math]()

1/2
Вычислить![math]()

4
Вычислить![math]()

3/2
Вычислить![math]()

1
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Являются ли функции ![math]() и
и ![math]() эквивалентными друг другу при
эквивалентными друг другу при ![math]() ?
? ![math]() ,
, ![math]() ,
, ![math]()
 и
и  эквивалентными друг другу при
эквивалентными друг другу при  ?
?  ,
,  ,
, 
(1) нет
(2) да
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) нет
(2) да
Пользуясь свойством непрерывности функции, определить, принимает ли функция ![math]() на заданном интервале данное значение?
на заданном интервале данное значение? ![math]() ,
, ![math]() ,
, ![math]()
 на заданном интервале данное значение?
на заданном интервале данное значение?  ,
,  ,
, 
(1) нет
(2) да
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть тело движется по закону ![math]() . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени ![math]()
 . Найти ускорение и скорость тела в момент времени
. Найти ускорение и скорость тела в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

2.0025
Приближенно вычислить данное значение, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]()

0.496
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

2
Вычислить ![math]()

1
Найти наибольший элемент множества ![math]()

1
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
484
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
5
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
1
Найти количество экстремумов у функции ![math]()
![math]() .
.

 .
.
2
Указать наименьший элемент множества ![math]()

1
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вниз?
является выпуклой вниз?
 является выпуклой вниз?
является выпуклой вниз?
(1) 3
(2) 2
(3) 1
(4) 0
(5) -1
(6) -2
При каком из перечисленных значении аргумента функция ![math]() является выпуклой вниз?
является выпуклой вниз?
 является выпуклой вниз?
является выпуклой вниз?
(1) 0
(2) -1
(3) -2
(4) -3
(5) -4
(6) -5
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) 5
(2) 7
(3) 0
(4) 1
(5) 3
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]()

1/9
Вычислить![math]()

1/6
Вычислить![math]()

-1/9
Вычислить![math]()

4/7
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
3
Подобрать параметр ![math]() так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины ![math]() и
и ![math]() были эквивалентными друг другу при
были эквивалентными друг другу при ![math]() .
. ![math]() ,
, ![math]() ,
, ![math]()
 так, чтобы бесконечно малые величины
так, чтобы бесконечно малые величины  и
и  были эквивалентными друг другу при
были эквивалентными друг другу при  .
.  ,
,  ,
, 
-2
Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Выберите график, соответствующий данной функции ![math]() .
. ![math]()
 .
. 
(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

В прямоугольнике стороны меняются по следующему закону ![math]() . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени ![math]()
 . Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени
. Узнать, с какой скоростью меняется площадь и периметр данного прямоугольника в момент времени 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.015
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.![math]() ,
, ![math]()
 в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой.
в данной точке, используя понятие дифференциала. Округлите значение до 4 знаков после запятой. ,
, 
1.0075
Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти ![math]() , если
, если ![math]()
 , если
, если 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]()

3
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Какова целая часть ![math]() ?
? ![math]()
 ?
? 
-34
Какова целая часть ![math]() ?
? ![math]()
 ?
? 
83
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
8
Найти значение функции ![math]()
![math]() в точке локального максимума.
в точке локального максимума.

 в точке локального максимума.
в точке локального максимума.
1
Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) 2
(2) -2
(3) -1
(4) точек перегиба нет
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 0.5
(2) 2
(3) -4
(4) точек перегиба нет
(5) 1
(6) 0
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -1
(2) 1
(3) 0
(4) -2
(5) 2
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Вычислить![math]()

3/2
Вычислить![math]()

-4/3
Вычислить![math]()

-7/12
Вычислить![math]()

1/70
Вычислить предел, используя асимптотические формулы ![math]()

(1) ln 7
(2) ln 8
(3) ln 9
(4) ln 10
Вычислить предел, используя асимптотические формулы ![math]()

1
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Пусть закон радиоактивного распада вещества записывается следующим образом: ![math]()
![math]() . Чему равна скорость распада момент времени
. Чему равна скорость распада момент времени ![math]() ?
?

 . Чему равна скорость распада момент времени
. Чему равна скорость распада момент времени  ?
?
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Количество электричества, протекающее через проводник, начиная с момента ![math]() , задается формулой
, задается формулой ![math]() . В какой момент времени сила тока равна
. В какой момент времени сила тока равна ![math]() ?
?
 , задается формулой
, задается формулой  . В какой момент времени сила тока равна
. В какой момент времени сила тока равна  ?
?
3
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.03
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
-0.06
Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить вторую производную ![math]() от функции, заданной параметрически:
от функции, заданной параметрически: ![math]()
 от функции, заданной параметрически:
от функции, заданной параметрически: 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить ![math]()

1
Вычислить ![math]()

1
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 3
(3) 0
(4) ![math]()

(5) ![math]()

(6) -1
Вычислить предел ![math]()

-8
Вычислить предел ![math]()

-6
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
С помощью производной определите, какие из неравенств верны.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]()
 при
при 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точку перегиба функции ![math]() .
.
 .
.
(1) 4
(2) точек перегиба нет
(3) 2
(4) -2
(5) 1
(6) 0
Найти точку перегиба функции ![math]() .
.
 .
.
(1) 16
(2) точек перегиба нет
(3) 8
(4) -8
(5) 1
(6) 0
Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -0.1
(2) 0.1
(3) 0.9
(4) -0.9
(5) 1
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

5/2
Вычислить![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить предел, используя асимптотические формулы ![math]()

2
Вычислить предел, используя асимптотические формулы ![math]()

(1) ln 5/ln 3
(2) ln 4/ln 3
(3) ln 9/ln 2
(4) ln 12/ln 6
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9925
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9925
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени ![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени
— время в секундах, измеренное с начала движения. Чему равна скорость движения в момент времени  ?
?
-1
Материальная точка движется прямолинейно по закону ![math]() , где
, где ![math]() — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах, ![math]() — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени ![math]() ускорение точки было равным
ускорение точки было равным ![math]()
![math]() ?
?
 , где
, где  — расстояние от точки отсчета в метрах,
— расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. В какой момент времени
— время в секундах, измеренное с начала движения. В какой момент времени  ускорение точки было равным
ускорение точки было равным 
 ?
?
1
Вычислить ![math]()

4
Вычислить ![math]()

1
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

При каких ![math]() имеет место равенство
имеет место равенство ![math]()
 имеет место равенство
имеет место равенство 
30
Найти ![math]()

0
С помощью производной определите, какие из неравенств верны.
(1) ![math]() <
< ![math]()
 <
< 
(2) ![math]() >
> ![math]()
 >
> 
(3) ![math]() <
< ![math]()
 <
< 
(4) ![math]() >
> ![math]()
 >
> 
С помощью производной, определите какие из неравенств верны.
(1) ![math]() >
> ![math]()
 >
> 
(2) ![math]() <
< ![math]()
 <
< 
(3) ![math]() >
> ![math]()
 >
> 
(4) ![math]() <
< ![math]()
 <
< 
Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Найти точку перегиба функции ![math]()

0
Найти точку перегиба функции ![math]()

0
Укажите наибольшее значение функции ![math]()

(1) -1.5
(2) 1.5
(3) 0
(4) -2
(5) 2
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

Вычислить![math]() , если
, если ![math]()
 , если
, если 
-7
Вычислить![math]()

7/12
Вычислить![math]()

-10
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.97
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.9625
Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Для функции ![math]() найти третий дифференциал
найти третий дифференциал ![math]()
 найти третий дифференциал
найти третий дифференциал 
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

-8
Вычислить ![math]()

1
Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

3
Найти ![math]() такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при ![math]()
![math]()
 такое, чтобы была верна приближенная формула при
такое, чтобы была верна приближенная формула при 

0
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли равенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) горизонтальных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Укажите ординату точки пересечения графика функции ![math]() с осью OY
с осью OY
 с осью OY
с осью OY
(1) 1
(2) нет
(3) 2
(4) ![math]()

(5) -2
(6) 0
Укажите наибольшее значение функции ![math]()

(1) -1
(2) 0.9
(3) 0
(4) -0.5
(5) 0.5
(6) нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
-1
Вычислить![math]() , если
, если ![math]()
 , если
, если 
4
Вычислить![math]()

7/15
Вычислить![math]()

8/3
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
0.4775
Вычислите приближенно значение функции ![math]() в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала: ![math]() ,
, ![math]() . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
 в данной точке, используя понятие дифференциала:
в данной точке, используя понятие дифференциала:  ,
,  . Округлите значение до 4 знаков после запятой.
. Округлите значение до 4 знаков после запятой.
1.5073
Вычислить ![math]()

-1
Вычислить ![math]()

1
Отметить счетные множества
(1) 7Z - Множество целых чисел, кратных 7
(2) множество натуральных чисел, являющихся 7-ми степенями ![math]()

(3) множество положительных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]()

(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Является ли счетным множество ![math]()

(1) да
(2) нет
Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Найти асимптоты графика функции ![math]() . Варианты ответа:
. Варианты ответа:
 . Варианты ответа:
. Варианты ответа:
(1) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(2) вертикальных асимптот нет
(3) ![math]() –наклонная асимптота
–наклонная асимптота
 –наклонная асимптота
–наклонная асимптота
(4) наклонных асимптот нет
(5) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(6) ![math]() – наклонная асимптота
– наклонная асимптота
 – наклонная асимптота
– наклонная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/6
Вычислить![math]()

1/3
Вычислить![math]()

3
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить ![math]()

2
Вычислить ![math]()

1
Найти точную верхнюю грань множества ![math]()

4
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() и
и ![math]()
 и
и 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() и
и ![math]() ; убывает на
; убывает на ![math]() и
и ![math]()
 и
и  ; убывает на
; убывает на  и
и 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти интервал монотонности функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(2) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(3) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(4) возрастает на ![math]() ; убывает на
; убывает на ![math]()
 ; убывает на
; убывает на 
(5) функция монотонна на всей числовой прямой
Найти точную верхнюю грань множества ![math]()

10
Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Найти асимптоты графика функции ![math]() .
.
 .
.
(1) вертикальных асимптот нет
(2) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота
(3) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(4) ![math]() – вертикальная асимптота
– вертикальная асимптота
 – вертикальная асимптота
– вертикальная асимптота
(5) горизонтальных асимптот нет
(6) ![math]() – горизонтальная асимптота
– горизонтальная асимптота
 – горизонтальная асимптота
– горизонтальная асимптота Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/8
Вычислить![math]()

-1
Вычислить![math]()

-5/3
Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Вычислить производную функции ![math]() , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
 , пользуясь правилами и формулами дифференцирования.
, пользуясь правилами и формулами дифференцирования.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Найти точную нижнюю грань множества ![math]()

3
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
16
Найти точную нижнюю грань множества ![math]()

-10
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Найти наклонные асимптоты графика функции ![math]() .
.
 .
.
(1) ![math]() при
при ![math]()
 при
при 
(2) ![math]() при
при ![math]() и
и ![math]()
 при
при  и
и 
(3) ![math]() при
при ![math]()
 при
при 
(4) ![math]() при
при ![math]()
 при
при 
(5) ![math]() при
при ![math]()
 при
при 
(6) наклонных асимптот нет
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]() , если
, если ![math]()
 , если
, если 
2
Вычислить![math]()

1/3
Вычислить![math]()

1/6
Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
(1)
![math]()

(2)
![math]()

Вычислить значение производной функции ![math]() в точке
в точке ![math]()
 в точке
в точке 
0
Найти точную верхнюю грань множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) ![math]()

(5) не существует
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
0
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
1
Найти точную верхнюю грань множества ![math]()

1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Вычислить![math]()

1/6
Вычислить![math]()

0
Найти наименьший элемент множества ![math]()

(1) не существует
(2) 0
(3) 1
(4) ![math]()

(5) 8
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) функция монотонна на всей числовой прямой
Найти точную нижнюю грань множества ![math]()

4
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/12
Вычислить![math]() , если
, если ![math]()
 , если
, если 
50/99
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-2
Найти ![math]() для функции
для функции ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 для функции
для функции  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) функция монотонна на всей числовой прямой
Найти ![math]() для функции
для функции ![math]()
 для функции
для функции 
1
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

-3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
3/2
Вычислить![math]() , если
, если ![math]()
 , если
, если 
0
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
2
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Определить, выполняется ли неравенство ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) да
(2) нет
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-5
Вычислить![math]() , если
, если ![math]()
 , если
, если 
1/3
Вычислить![math]() , если
, если ![math]()
 , если
, если 
6
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Сравнить числа ![math]() и
и ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и
и  и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
41230
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 3
(2) 9
(3) 2
(4) 4
(5) 8
(6) 27
Вычислить ![math]()

0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
13/9
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/180
Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

-1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

0
Вычислить ![math]()

(1) ![math]()

(2) ![math]()

Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) 0
(7) -2
(8) -1
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

(1) ![math]()

(2)
![math]()

Вычислить ![math]()

1
Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 3
Указать наименьший элемент множества ![math]()

5
Вычислить ![math]()

0
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) -3
(3) 0
(4) ![math]()

(5) ![math]()

(6) -1
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) -1
(4) -2
(5) -3
(6) 0,5
Вычислить ![math]()

-1
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Вычислить ![math]()

2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 8Z - Множество целых чисел, кратных 8
(2) множество натуральных чисел, являющихся 8-ми степенями ![math]()

(3) множество положительных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Вычислить ![math]()

2
Вычислить ![math]() и вписать номер правильного ответа:
и вписать номер правильного ответа:
 и вписать номер правильного ответа:
и вписать номер правильного ответа:
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти точную верхнюю грань множества ![math]()

2
Найти точную верхнюю грань множества ![math]()

3
Найти точную нижнюю грань множества ![math]()

1
Найти точную нижнюю грань множества ![math]()

0
Найти наименьший элемент множества ![math]()

2/3
Найти точную нижнюю грань множества ![math]()

0
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

-1
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
4
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-7
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
8990
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 3
(2) 9
(3) 2
(4) 4
(5) 8
(6) 27
Вычислить ![math]()

1
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/30
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
7/900
Вычислить ![math]()

1
Вычислить ![math]()

0
Вычислить ![math]()

0
Вычислить ![math]()

8
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) -3
(5) ![math]()

(6) ![math]()

(7) 0
(8) -1
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

0
Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 4
Указать наименьший элемент множества ![math]()

3
Вычислить ![math]()

0
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

0
Отметьте значения, принадлежащие данному множеству ![math]()

(1) -1
(2) 3
(3) 0
(4) ![math]()

(5) ![math]()

(6) 1
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) -1
(4) -2
(5) 2
(6) 0,5
Вычислить ![math]()

0
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Вычислить ![math]()

0
Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Вычислить ![math]()

0
Отметить счетные множества
(1) 9Z - Множество целых чисел, кратных 9
(2) множество натуральных чисел, являющихся 9-ми степенями ![math]()

(3) множество положительных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Вычислить ![math]()

1
Найти точную верхнюю грань множества ![math]()

3
Найти точную верхнюю грань множества ![math]()

2
Найти точную нижнюю грань множества ![math]()

0
Найти точную нижнюю грань множества ![math]()

-5
Найти наименьший элемент множества ![math]()

3/4
Найти точную нижнюю грань множества ![math]()

3
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

1
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
5
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-7
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, вычислить значение этого выражения ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
40319
При помощи математической индукции доказать, что при любом натуральном n>0 выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 4
(2) 37
(3) 148
(4) 3
(5) 6
(6) 9
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
19/15
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/300
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 2
(4) -4
(5) ![math]()

(6) ![math]()

(7) -2
(8) 0
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 5
Указать наименьший элемент множества ![math]()

-7
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) -2
(2) -3
(3) 0
(4) ![math]()

(5) ![math]()

(6) 2
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 3
(7) 0,5
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 10Z - Множество целых чисел, кратных 10
(2) множество натуральных чисел, являющихся 10-ми степенями ![math]()

(3) множество отрицательных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Найти точную верхнюю грань множества ![math]()

4
Найти точную верхнюю грань множества ![math]()

-4
Найти точную нижнюю грань множества ![math]()

2
Найти точную нижнюю грань множества ![math]()

-8
Найти наименьший элемент множества ![math]()

4/5
Найти точную нижнюю грань множества ![math]()

0
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
0
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

3
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
6
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-1
Установить, чему равняется ![math]() при помощи математической индукции
при помощи математической индукции
 при помощи математической индукции
при помощи математической индукции
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
10660
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 3
(2) 2
(3) 6
(4) 9
(5) 12
(6) 5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
97/45
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/825
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) -1
(4) ![math]()

(5) ![math]()

(6) ![math]()

(7) ![math]()

(8) ![math]()

Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 6
Указать наименьший элемент множества ![math]()

-5
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) 2
(2) 3
(3) 0
(4) ![math]()

(5) ![math]()

(6) -2
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 3
(7) 0,5
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 11Z - Множество целых чисел, кратных 11
(2) множество натуральных чисел, являющихся 11-ми степенями ![math]()

(3) множество отрицательных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Найти точную верхнюю грань множества ![math]()

2
Найти точную верхнюю грань множества ![math]()

-3
Найти точную нижнюю грань множества ![math]()

1/2
Найти точную нижнюю грань множества ![math]()

-6
Найти наименьший элемент множества ![math]()

5/6
Найти точную нижнюю грань множества ![math]()

-99
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-2
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

6
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
2
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-4
Установить, чему равняется ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
44100
При помощи математической индукции можно доказать, что при любом натуральном n выражение ![math]() делится на ...
делится на ...
 делится на ...
делится на ...
(1) 2
(2) 3
(3) 6
(4) 7
(5) 42
(6) 4
(7) 5
(8) 8
(9) 9
(10) 12
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
35/9
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
7/3300
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 1
(4) -3
(5) ![math]()

(6) ![math]()

(7) -4
(8) 2
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 7
Указать наименьший элемент множества ![math]()

1
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) 2
(2) -3
(3) 0
(4) ![math]()

(5) ![math]()

(6) -2
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) 2
(4) 3
(5) -1
(6) -2
(7) 4
(8) 0,5
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 12Z - Множество целых чисел, кратных 12
(2) множество натуральных чисел, являющихся 12-ми степенями ![math]()

(3) множество отрицательных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Найти точную верхнюю грань множества ![math]()

3
Найти точную верхнюю грань множества ![math]()

0
Найти точную нижнюю грань множества ![math]()

2
Найти точную нижнюю грань множества ![math]()

-4
Найти наименьший элемент множества ![math]()

6/7
Найти точную нижнюю грань множества ![math]()

1
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-3
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

9
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
2
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
1
Установить, чему равняется ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
325
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 2
(2) 3
(3) 6
(4) 4
(5) 8
(6) 12
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
82/45
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/150
Отметьте значения, удовлетворяющие данному неравенству ![math]()

(1) ![math]()

(2) ![math]()

(3) 2
(4) -4
(5) ![math]()

(6) ![math]()

(7) -5
(8) 4
Решить неравенство ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Найти наибольший элемент множества ![math]()

(1) 0
(2) 1
(3) ![math]()

(4) не существует
(5) 8
Указать наименьший элемент множества ![math]()

2
Отметить верные соотношения между множествами
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Задать множество перечислением элементов, если ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте значения, принадлежащие данному множеству ![math]()

(1) -2
(2) 3
(3) 0
(4) ![math]()

(5) ![math]()

(6) 2
Отметьте значения, принадлежащие данному множеству ![math]()

(1) 1
(2) 0
(3) 2
(4) 3
(5) 4
(6) -1
(7) -2
(8) 5
(9) 0,5
Изобразить графически точки множества А на плоскости ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

Изобразить на координатной плоскости множество ![math]()

(1) ![files]()

(2) ![files]()

(3) ![files]()

(4) ![files]()

(5) ![files]()

Зная А и В, найти объединение ![math]() и пересечение
и пересечение ![math]()
![math]()
 и пересечение
и пересечение 

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

(6) ![math]()

Пусть множество ![math]() и
и ![math]() . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что ![math]() .
.
 и
и  . Отметьте элементы, входящие в множество, если известно, что
. Отметьте элементы, входящие в множество, если известно, что  .
.
(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметить счетные множества
(1) 13Z - Множество целых чисел, кратных 13
(2) множество натуральных чисел, являющихся 13-ми степенями ![math]()

(3) множество отрицательных рациональных чисел ![math]()

(4) множество действительных чисел R
(5) множество всех точек отрезка ![math]()
![math]()


(6) множество всех точек интервала ![math]()
![math]()


Является ли счетным множество ![math]()

(1) да
(2) нет
Найти точную верхнюю грань множества ![math]()

4
Найти точную верхнюю грань множества ![math]()

9
Найти точную нижнюю грань множества ![math]()

3
Найти точную нижнюю грань множества ![math]()

4
Найти наименьший элемент множества ![math]()

7/8
Найти точную нижнюю грань множества ![math]()

1
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
-2
Найти точную верхнюю грань множества ![math]() , если
, если ![math]()
![math]()
 , если
, если 

9
Даны два множества ![math]() . Пусть
. Пусть![math]() Найти
Найти ![math]()
 . Пусть
. Пусть Найти
Найти 
4
Найти точную нижнюю грань множества ![math]() , если
, если ![math]() ,
, ![math]()
 , если
, если  ,
, 
-1
Установить, чему равняется ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Используя метод математической индукции, найти ![math]() и вычислить значение этого выражения при
и вычислить значение этого выражения при ![math]()
 и вычислить значение этого выражения при
и вычислить значение этого выражения при 
10000
При помощи математической индукции доказать, что при любом натуральном n выражение ![math]() делится на K
делится на K
 делится на K
делится на K
(1) 2
(2) 3
(3) 6
(4) 8
(5) 9
(6) 12
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
4/9
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
2/225
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) -1
(4) -2
(5) 2
(6) 0,5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
2/3
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
7/4950
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 4
(7) 0,5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/3
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/550
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) -1
(4) -2
(5) 2
(6) 0,5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
13/99
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/300
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 3
(7) 0,5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
3/11
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
1/396
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 5
(7) 0,5
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
7/9
Представить число ![math]() в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
 в виде несократимой рациональной дроби p/q
в виде несократимой рациональной дроби p/q
19/9900
Отметьте элементы множества ![math]()

(1) ![math]()

(2) ![math]()

(3) ![math]()

(4) ![math]()

(5) ![math]()

Отметьте элементы множества ![math]()

(1) 1
(2) 0
(3) 2
(4) -1
(5) -2
(6) 5
(7) 0,5
(8) 3