Главная /
Математика /
Дифференциальные уравнения и краевые задачи
Дифференциальные уравнения и краевые задачи - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс лекций посвящен изложению методов и теории дифференциальных уравнений и краевых задач.
Все ответы: Курс лекций посвящен изложению методов и теории дифференциальных уравнений и краевых задач.
Задано дифференциальное уравнение второго порядка с переменными коэффициентами: ![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 60 |
| c | 10 |
| f | 12 |
| g | 5 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-12
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение 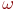 .
.
2
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
3
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 3 |
| b | 5 |
 .
.
5
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
`4
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -8 |
| a12 | 4 |
| a21 | -12 |
| a22 | 6 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
2
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | 14 |
| a12 | 4 |
| a21 | -4 |
| a22 | 6 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 60 |
| c | 10 |
| f | 12 |
| g | 5 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-15
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
3
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
4
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 3 |
| b | 5 |
 .
.
3
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
-24
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -8 |
| a12 | 4 |
| a21 | -12 |
| a22 | 6 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
3
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | 14 |
| a12 | 4 |
| a21 | -4 |
| a22 | 6 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 60 |
| c | 10 |
| f | 12 |
| g | 5 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
5
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
4
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 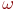 .
.
2
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 3 |
| b | 5 |
 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
-267
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -8 |
| a12 | 4 |
| a21 | -12 |
| a22 | 6 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
4
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | 14 |
| a12 | 4 |
| a21 | -4 |
| a22 | 6 |
10
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 60 |
| c | 10 |
| f | 12 |
| g | 5 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение 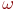 .
.
2
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
4
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
5
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 3 |
| b | 5 |
 .
.
5
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
-1071
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -13 |
| a12 | 4 |
| a21 | -22 |
| a22 | 6 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
6
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | 14 |
| a12 | 4 |
| a21 | -4 |
| a22 | 6 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 48 |
| c | 8 |
| f | 24 |
| g | 2 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-48
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
6
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 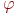 . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.
-0,644
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 3 |
| b | 5 |
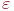 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
12279
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -7 |
| a12 | 7 |
| a21 | -4 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
4
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | -26 |
| a12 | 4 |
| a21 | -64 |
| a22 | 6 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 48 |
| c | 8 |
| f | 24 |
| g | 2 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-12
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
4
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
6
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 3 |
| b | 5 |
 , если:
, если:
| A | 12 |
| B | 3 |
6
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
49290
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -7 |
| a12 | 7 |
| a21 | -4 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
6
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | -26 |
| a12 | 4 |
| a21 | -64 |
| a22 | 6 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 48 |
| c | 8 |
| f | 24 |
| g | 2 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
4
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
6
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
8
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 3 |
| b | 5 |
 , если:
, если:
| A | 6 |
| B | 9 |
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
917797
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | -26 |
| a12 | 4 |
| a21 | -64 |
| a22 | 6 |
-10
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 48 |
| c | 8 |
| f | 24 |
| g | 2 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
2
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 2 |
| a1 | 3 |
| b0 | 4 |
| b1 | 1 |
| a | 0 |
| b |  |
| A | 26 |
| B | 22 |
| k | 4 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
4
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 3 |
| q | 12 |
| A | 4 |
| B | 6 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
4
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 3 |
| b | 5 |
 , если:
, если:
| A | 3 |
| B | 8 |
-5
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 3 |
| a1 | 4 |
| a2 | 5 |
| a3 | 2 |
| a4 | 4 |
| a5 | 1 |
| a6 | 2 |
| a7 | 6 |
| a8 | 9 |
| a9 | 7 |
 .
.
8260173
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | -26 |
| a12 | 4 |
| a21 | -64 |
| a22 | 6 |
1
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 168 |
| c | 13 |
| f | 24 |
| g | 7 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-48
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение 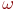 .
.
3
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
6
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 2 |
| b | 3 |
 .
.
3
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
9
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -15 |
| a12 | 3 |
| a21 | -60 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
3
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | -6 |
| a12 | 3 |
| a21 | -27 |
| a22 | 12 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 168 |
| c | 13 |
| f | 24 |
| g | 7 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-42
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
2
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
8
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 2 |
| b | 3 |
 .
.
2
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
-111
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -15 |
| a12 | 3 |
| a21 | -60 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
2
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | -6 |
| a12 | 3 |
| a21 | -27 |
| a22 | 12 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 168 |
| c | 13 |
| f | 24 |
| g | 7 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
6,2
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 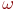 .
.
4
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 2 |
| b | 3 |
 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
-657
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -15 |
| a12 | 3 |
| a21 | -60 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
7
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | -6 |
| a12 | 3 |
| a21 | -27 |
| a22 | 12 |
3
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 288 |
| b | 168 |
| c | 13 |
| f | 24 |
| g | 7 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение 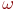 .
.
1
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
10
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 2 |
| b | 3 |
 .
.
3
Условия.
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
-375
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -19 |
| a12 | 3 |
| a21 | -80 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
6
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | -6 |
| a12 | 3 |
| a21 | -27 |
| a22 | 12 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() ,
, ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 17 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: ,
,  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-108
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
6
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 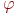 . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.
-0,644
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 2 |
| b | 3 |
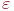 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
25515
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -19 |
| a12 | 3 |
| a21 | -80 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
-7
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | -18 |
| a12 | 3 |
| a21 | -75 |
| a22 | 12 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 17 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-27
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
-7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]()

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне 
32
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 2 |
| b | 3 |
 , если:
, если:
| A | 14 |
| B | 2 |
6
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
169775
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -19 |
| a12 | 3 |
| a21 | -80 |
| a22 | 12 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
-6
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | -18 |
| a12 | 3 |
| a21 | -75 |
| a22 | 12 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 17 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
8,5
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
-6
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
16
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 2 |
| b | 3 |
 , если:
, если:
| A | 12 |
| B | 3 |
4,5
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
441937
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | -18 |
| a12 | 3 |
| a21 | -75 |
| a22 | 12 |
-3
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки: .
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 17 |
| f | 36 |
| g | 3 |
 , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
1
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 3 |
| a1 | 1 |
| b0 | 7 |
| b1 | 6 |
| a | 0 |
| b |  |
| A | 27 |
| B | -85 |
| k | 9 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 6 |
| q | 96 |
| A | 8 |
| B | 24 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
8
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 2 |
| b | 3 |
 , если:
, если:
| A | 7 |
| B | 5 |
1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 1 |
| a1 | 5 |
| a2 | 3 |
| a3 | 6 |
| a4 | 7 |
| a5 | 2 |
| a6 | 4 |
| a7 | 8 |
| a8 | 3 |
| a9 | 2 |
 .
.
1325811
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | -18 |
| a12 | 3 |
| a21 | -75 |
| a22 | 12 |
1
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 27 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-108
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение 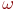 .
.
4
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
5
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 1 |
| b | 4 |
 .
.
4
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
38
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -7 |
| a12 | 7 |
| a21 | -4 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
9
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | 4 |
| a12 | 7 |
| a21 | 0 |
| a22 | 4 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 27 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
-27
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
5
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
12
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 1 |
| b | 4 |
 .
.
1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
226
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -7 |
| a12 | 7 |
| a21 | -4 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
5
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | 4 |
| a12 | 7 |
| a21 | 0 |
| a22 | 4 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 27 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение  .
.
13,5
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  , удовлетворяющее краевой задаче.
, удовлетворяющее краевой задаче.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 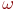 .
.
5
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 1 |
| b | 4 |
 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
-1548
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -7 |
| a12 | 7 |
| a21 | -4 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
7
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | 4 |
| a12 | 7 |
| a21 | 0 |
| a22 | 4 |
4
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 648 |
| b | 108 |
| c | 27 |
| f | 36 |
| g | 3 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: .
В ответе укажите значение
.
В ответе укажите значение 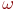 .
.
3
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение  .
.
13
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 1 |
| b | 4 |
 .
.
4
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
5142
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
| a11 | -11 |
| a12 | 7 |
| a21 | -8 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение дискриминанта характеристического уравнения.
20
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | 4 |
| a12 | 7 |
| a21 | 0 |
| a22 | 4 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 12 |
| c | -3 |
| f | 12 |
| g | 1 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-12
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
20
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать значение
.
В ответе указать значение 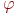 . В ответе привести три цифры после десятичной запятой.
. В ответе привести три цифры после десятичной запятой.
-0,395
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() .
.
| a | 1 |
| b | 4 |
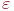 .
.
-1
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
-59994
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
| a11 | -11 |
| a12 | 7 |
| a21 | -8 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наименьшего из корней характеристического уравнения.
7
Дана система дифференциальных уравнений:
Найдите дискриминант характеристического уравнения.
| a11 | -10 |
| a12 | 7 |
| a21 | -7 |
| a22 | 4 |
0
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 12 |
| c | -3 |
| f | 12 |
| g | 1 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-3
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
40
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 1 |
| b | 4 |
 , если:
, если:
| A | 10 |
| B | 4 |
6
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
-564271
Дана система дифференциальных уравнений:
Рассмотрите фазовую плоскость:![math]() , где
, где ![math]() (
(![math]() – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
| a11 | -11 |
| a12 | 7 |
| a21 | -8 |
| a22 | 4 |
 , где
, где  (
( – корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
– корни характеристического уравнения системы).
В ответе указать значение наибольшего из корней характеристического уравнения.
20
Дана система дифференциальных уравнений:
Определите кратность корней характеристического уравнения (1 или 2).
| a11 | -10 |
| a12 | 7 |
| a21 | -7 |
| a22 | 4 |
2
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 12 |
| c | -3 |
| f | 12 |
| g | 1 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
-1,5
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
20
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
20
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 1 |
| b | 4 |
 , если:
, если:
| A | 9 |
| B | 2 |
7
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
10339291
Дана система дифференциальных уравнений:
Найдите корень характеристического уравнения.
| a11 | -10 |
| a12 | 7 |
| a21 | -7 |
| a22 | 4 |
-3
Задано дифференциальное уравнение второго порядка с переменными коэффициентами:![math]() , где
, где
Найти решение с помощью подстановки:![math]() .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид:![math]() , где
, где ![math]() .
В ответе укажите значение
.
В ответе укажите значение ![math]() .
.
 , где
, где
| a | 72 |
| b | 12 |
| c | -3 |
| f | 12 |
| g | 1 |
 .
Показать, что решение имеет вид:
.
Показать, что решение имеет вид: , где
, где  .
В ответе укажите значение
.
В ответе укажите значение  .
.
3
Задана краевая задача:
Для дифференциального уравнения:![math]() .
.
Показать, что решение имеет вид:![math]() .
В ответе указать значение
.
В ответе указать значение ![math]() .
.
 .
.
| a0 | 7 |
| a1 | 4 |
| b0 | 6 |
| b1 | 2 |
| a | 0 |
| b |  |
| A | 129 |
| B | 82 |
| k | 16 |
 .
В ответе указать значение
.
В ответе указать значение  .
.
7
Дана задача Коши для дифференциального уравнения:
![math]()
Показать, что решение имеет вид:
![math]() А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
![math]() Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне ![math]() и
и ![math]() и
и ![math]() .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне ![math]() .
.

| p | 7 |
| q | 175 |
| A | 12 |
| B | 25 |
 А также, что решение может быть представлено в виде:
А также, что решение может быть представлено в виде:
 Найти сколько корней имеет решение в диапазоне
Найти сколько корней имеет решение в диапазоне  и
и  и
и  .
В ответе указать, сколько корней имеет решение в диапазоне
.
В ответе указать, сколько корней имеет решение в диапазоне  .
.
10
Дана система дифференциальных уравнений:
Показать, что первыми интегралами системы являются выражения вида:
В ответе указать значение ![math]() , если:
, если:
| a | 1 |
| b | 4 |
 , если:
, если:
| A | 8 |
| B | 3 |
5
Дано характеристическое уравнение:
![math]()
Составить матрицу Гурвица и вычислить значение главного диагонального минора ![math]() .
.

| a0 | 6 |
| a1 | 7 |
| a2 | 8 |
| a3 | 3 |
| a4 | 2 |
| a5 | 5 |
| a6 | 6 |
| a7 | 7 |
| a8 | 5 |
| a9 | 9 |
 .
.
51696455
Дана система дифференциальных уравнений:
Определите устойчиво (1) или неустойчиво (2) решение системы в начале координат.
| a11 | -10 |
| a12 | 7 |
| a21 | -7 |
| a22 | 4 |
1