Главная /
Математика /
Численные методы
Численные методы - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс знакомит с численными методами и возможностью их применения на практике.
Все ответы: Курс знакомит с численными методами и возможностью их применения на практике.
Смотрите также:
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,025
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,25
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | 2 | 7 | |
| 7 | 3 | 27 |
5
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
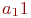 .
.
| 1 | 2 |
| 7 | 3 |
3
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 2 |
| 1 | 2 | 7 | |
| 7 | 3 | 27 |
5
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -7 | 12 | 4 |
-2
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
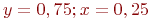 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,196
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
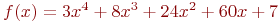 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
-264
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
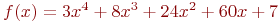 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,528948
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
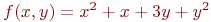 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,5
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
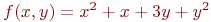 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,33
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,023
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
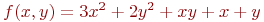 .
Имеется условие:
.
Имеется условие:
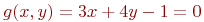 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
(1) f=41; g=17
(2) f=143; g=22
(3) f=131; g=36
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 2 | 6 | 0 | 1 | 72 |
| 1 | -3 | -6 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 60 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 16 | 80 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 0 | 25 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,850
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,5243
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 2. Чему равно
равна 2. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,8
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 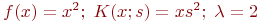 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0134
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 16 |
| 3 | 28 |
| 4 | 34 |
| 5 | 47 |
| 6 | 59 |
| 7 | 62 |
| 8 | 74 |
| 9 | 85 |
| 10 | 96 |
| 11 | 106 |
| 12 | 117 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
9,874
В урне 5 белых и 6 черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Найти вероятность того, что оба шара будут белыми.
(1) 2/11
(2) 1/6
(3) 3/11
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,187
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
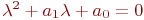 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 4 |
| 5 | 2 |
 .
.
5
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
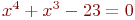 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,75
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,023
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
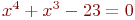 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,93958
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,887
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
0,0000014
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
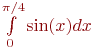 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0021
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
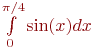 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
7430
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000134
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,04
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,875
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 4 | 1 | 3 | 29 | |
| 3 | 3 | 4 | 32 | |
| 2 | 5 | 7 | 39 |
10
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
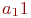 .
.
| 4 | 1 | 3 |
| 3 | 3 | 4 |
| 2 | 5 | 7 |
1
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 3 |
 | 2 |
| 4 | 1 | 3 | 29 | |
| 3 | 3 | 4 | 32 | |
| 2 | 5 | 7 | 39 |
10
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -12 | 47 | -60 | 5 |
6
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
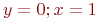 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,4764
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
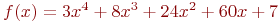 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
14448982335
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
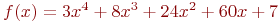 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-40,831794
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
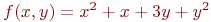 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,5
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
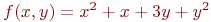 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,23
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00032
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти при каких значениях
.
Найти при каких значениях ![math]() и
и ![math]() достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
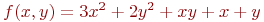 .
Имеется условие:
.
Имеется условие:
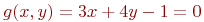 .
Найти при каких значениях
.
Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (0,037;0,222)
(2) (-1,030;-0,424)
(3) (-0,186;-0,514)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 6 | 6 | 0 | 1 | 72 |
| 1 | -4 | -9 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 90 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 46 | 70 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 20 | 35 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,989
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,5262
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1. Чему равно
равна 1. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,1
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 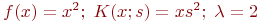 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0539
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 16 |
| 3 | 28 |
| 4 | 34 |
| 5 | 47 |
| 6 | 59 |
| 7 | 62 |
| 8 | 74 |
| 9 | 85 |
| 10 | 96 |
| 11 | 106 |
| 12 | 117 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-3,181
В урне 5 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут разных цветов.
(1) 6/11
(2) 1/2
(3) 5/11
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,964
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
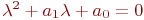 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 4 |
| 5 | 2 |
 .
.
14
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
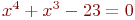 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,125
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
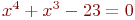 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,125
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
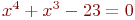 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
-1,55067
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,030
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000996
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
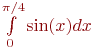 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0021
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
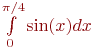 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
6658
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000008
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность 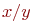 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,065
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
-0,6875
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 4 | 1 | 4 | 5 | 46 | |
| 5 | 6 | 2 | 1 | 42 | |
| 7 | 3 | 3 | 4 | 53 | |
| 1 | 2 | 2 | 2 | 24 |
13
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
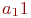 .
.
| 4 | 1 | 4 | 5 |
| 5 | 6 | 2 | 1 |
| 7 | 3 | 3 | 4 |
| 1 | 2 | 2 | 2 |
-8
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 4 |
 | 1 |
 | 6 |
| 4 | 1 | 4 | 5 | 46 | |
| 5 | 6 | 2 | 1 | 42 | |
| 7 | 3 | 3 | 4 | 53 | |
| 1 | 2 | 2 | 2 | 24 |
13
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -13 | 59 | -107 | 60 | 1 |
-24
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
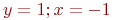 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,875
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
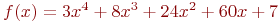 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
93
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
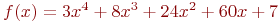 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,527191
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
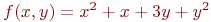 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
-0,6
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
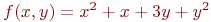 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,49
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,047
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
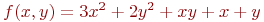 .
Имеется условие:
.
Имеется условие:
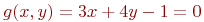 .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
(1) 0,370
(2) -4,788
(3) -2,796
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 1 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 6 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 8 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,192
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,5266
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5. Чему равно
равна 1,5. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,0
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 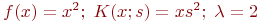 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,1214
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 16 |
| 3 | 28 |
| 4 | 34 |
| 5 | 47 |
| 6 | 59 |
| 7 | 62 |
| 8 | 74 |
| 9 | 85 |
| 10 | 96 |
| 11 | 106 |
| 12 | 117 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
9,666
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью хотя бы из одной урны извлечены 2 белых шара?
(1) 17/45
(2) 28/45
(3) 16/45
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,749
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
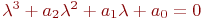 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 4 | 3 |
| 2 | 1 | 2 |
| 7 | 2 | 4 |
 .
.
8
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
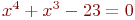 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,63
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,448
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
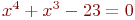 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,97691
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,448
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,00000002
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
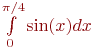 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
0,0000004
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
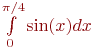 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
386
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000051
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 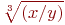 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,020
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,53125
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 5 | 5 | 7 | 1 | 6 | 68 | |
| 3 | 1 | 5 | 2 | 4 | 48 | |
| 2 | 4 | 3 | 2 | 3 | 44 | |
| 5 | 2 | 2 | 4 | 2 | 55 | |
| 2 | 3 | 6 | 3 | 1 | 41 |
17
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
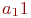 .
.
| 5 | 5 | 7 | 1 | 6 |
| 3 | 1 | 5 | 2 | 4 |
| 2 | 4 | 3 | 2 | 3 |
| 5 | 2 | 2 | 4 | 2 |
| 2 | 3 | 6 | 3 | 1 |
198
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 2 |
 | 1 |
 | 6 |
 | 5 |
| 5 | 5 | 7 | 1 | 6 | 68 | |
| 3 | 1 | 5 | 2 | 4 | 48 | |
| 2 | 4 | 3 | 2 | 3 | 44 | |
| 5 | 2 | 2 | 4 | 2 | 55 | |
| 2 | 3 | 6 | 3 | 1 | 41 |
17
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 1 | -20 | 150 | -520 | 809 | -420 | 7 |
0
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
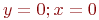 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
4,998
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
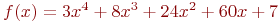 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
233316950
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
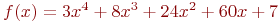 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-40,832012
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
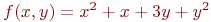 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
-1,0
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
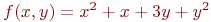 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,49
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00065
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
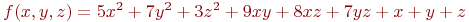 .
Имеется условие:
.
Имеется условие:
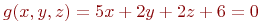 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
(1) f=592; g=40
(2) f=419; g=22
(3) f=385; g=44
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 2 | 2 | 1 | 0 | 0 | 10 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2,5 | 0 | 0 | 42 | 52,5 | 20 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,442
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,5267
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,75. Чему равно
равна 1,75. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,4
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 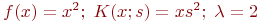 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,2159
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 16 |
| 3 | 28 |
| 4 | 34 |
| 5 | 47 |
| 6 | 59 |
| 7 | 62 |
| 8 | 74 |
| 9 | 85 |
| 10 | 96 |
| 11 | 106 |
| 12 | 117 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-1,833
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 2 орла и не менее 5-ти очков на игральной кости?
(1) 1/8
(2) 1/4
(3) 3/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-7,881
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
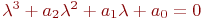 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 4 | 3 |
| 2 | 1 | 2 |
| 7 | 2 | 4 |
 .
.
14
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
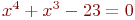 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9375
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
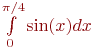 методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000001
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
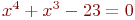 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 8-го знака после запятой (без округления).
-0,00000001
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,005
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000107
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
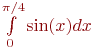 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 7-го знака после запятой (без округления).
0,0000009
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
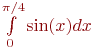 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
9336
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000072
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 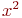 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,8
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,953125
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | 2 | 7 | |
| 7 | 3 | 27 |
-11
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 1 | 2 |
| 7 | 3 |
-0,0909
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 3 |
 | 0 |
| 1 | 2 | 7 | |
| 7 | 3 | 27 |
5
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -7 | 12 | 4 |
7
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
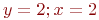 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,181
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
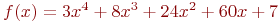 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
-11
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
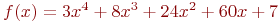 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,528277
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
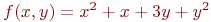 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,50
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
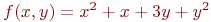 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,50
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,13
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
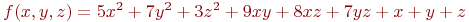 .
Имеется условие:
.
Имеется условие:
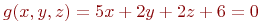 .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (-2,631;-0,157;3,736)
(2) (52,16;-5,8;-7,44)
(3) (-7,241;-4,517;5,655)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 7 | 3 | 2 | 1 | 0 | 0 | 15 |
| 0 | 6 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 7 | 16 | 7 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
5,658
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,4421
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,625. Чему равно
равна 1,625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,2
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 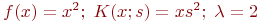 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,3374
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать коэффициенты эмпирической формулы ![math]() методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений ![math]() относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 16 |
| 3 | 28 |
| 4 | 34 |
| 5 | 47 |
| 6 | 59 |
| 7 | 62 |
| 8 | 74 |
| 9 | 85 |
| 10 | 96 |
| 11 | 106 |
| 12 | 117 |
 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,001
Вероятность выпадения дождя 3/4. Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку вдень экзамена 1/2. С какой вероятностью придётся мокнуть под дождём на платформе в плохом настроении, вызванном провалом на экзамене?
(1) 3/32
(2) 9/32
(3) 3/8
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,278
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
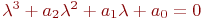 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 4 | 3 |
| 2 | 1 | 2 |
| 7 | 2 | 4 |
 .
.
15
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
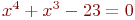 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
1,984375
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000010
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
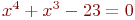 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 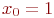 . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
-21
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,291
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000855
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
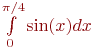 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,74
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
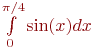 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
7430
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000102
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 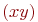 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
1,3
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
-0,0546875
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 4 | 1 | 3 | 29 | |
| 3 | 3 | 4 | 32 | |
| 2 | 5 | 7 | 39 |
18
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 4 | 1 | 3 |
| 3 | 3 | 4 |
| 2 | 5 | 7 |
0,0555
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 5 |
 | 3 |
 | 0 |
| 4 | 1 | 3 | 29 | |
| 3 | 3 | 4 | 32 | |
| 2 | 5 | 7 | 39 |
10
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -12 | 47 | -60 | 5 |
12
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
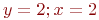 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,057
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
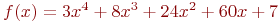 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
36922
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
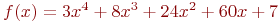 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-40,831899
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
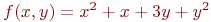 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,30
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
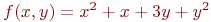 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,49
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0031
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
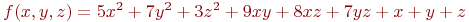 .
Имеется условие:
.
Имеется условие:
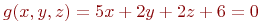 .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
(1) -1,421
(2) 430,36
(3) -98,172
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 5 | 2 | 1 | 0 | 20 |
| 0 | 3 | 1 | 0 | 1 | 35 |
| 1 | -4 | -6 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 25 | 60 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 20 | 1 | 16 | 60 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 10 | 0 | 20 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,822
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,6911
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5625. Чему равно
равна 1,5625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,1
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 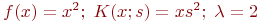 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,4859
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 43 |
| 3 | 85 |
| 4 | 167 |
| 5 | 259 |
| 6 | 354 |
| 7 | 501 |
| 8 | 630 |
| 9 | 819 |
| 10 | 1016 |
| 11 | 1220 |
| 12 | 1456 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,359
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа компьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью посадка пройдёт в штатном режиме? Ответ введите с точностью до 3-го знака после запятой (без округления).
0,087
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,920
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
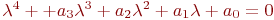 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 1 | 4 | 2 | 2 |
| 3 | 5 | 1 | 9 |
| 5 | 7 | 3 | 7 |
| 2 | 6 | 6 | 5 |
 .
.
14
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
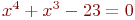 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,673
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 4 | 1 | 3 | 29 | |
| 3 | 3 | 4 | 32 | |
| 2 | 5 | 7 | 39 |
18
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
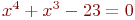 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 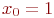 . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
7
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,162
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,00000001
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
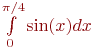 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,74
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
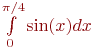 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
6658
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000217
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины 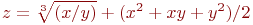 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
2,0
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
-0,98046875
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 4 | 1 | 4 | 5 | 46 | |
| 5 | 6 | 2 | 1 | 42 | |
| 7 | 3 | 3 | 4 | 53 | |
| 1 | 2 | 2 | 2 | 24 |
-29
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 4 | 1 | 4 | 5 |
| 5 | 6 | 2 | 1 |
| 7 | 3 | 3 | 4 |
| 1 | 2 | 2 | 2 |
-0,0344
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 2 |
 | 4 |
 | 1 |
 | 0 |
| 4 | 1 | 4 | 5 | 46 | |
| 5 | 6 | 2 | 1 | 42 | |
| 7 | 3 | 3 | 4 | 53 | |
| 1 | 2 | 2 | 2 | 24 |
13
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -13 | 59 | -107 | 60 | 1 |
13
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
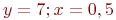 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,601
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
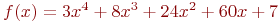 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
41
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
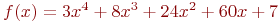 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,528277
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
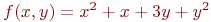 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,50
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
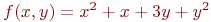 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-0,50
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,15
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
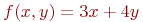 .
Имеется условие:
.
Имеется условие:
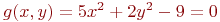 .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
(1) (-0,574;-1,916) и (0,574;1,916)
(2) (-0,340;-1,359) и (0,340;1,359)
(3) (-0,197;-1,834) и (0,197;1,834)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 6 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 6 | 1 | 0 | 1 | 0 | 80 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 160 |
| 1 | -4 | -8 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 20 | 120 | 80 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 20 | 0 | 0 | 30 | 70 | 80 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 10 | 0 | 0 | 0 | 30 | 80 | 120 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
3,359
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,6911
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,6. Чему равно
равна 1,6. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,1
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 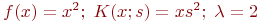 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,6614
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 43 |
| 3 | 85 |
| 4 | 167 |
| 5 | 259 |
| 6 | 354 |
| 7 | 501 |
| 8 | 630 |
| 9 | 819 |
| 10 | 1016 |
| 11 | 1220 |
| 12 | 1456 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-3,171
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы был Тибальд родственник Монтекки. Если бы не он всё обошлось бы без крови. С какой вероятностью никакой любви не случилось бы?
(1) 1/2
(2) 1/8
(3) 1/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-1,116
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
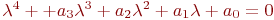 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 1 | 4 | 2 | 2 |
| 3 | 5 | 1 | 9 |
| 5 | 7 | 3 | 7 |
| 2 | 6 | 6 | 5 |
 .
.
61
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
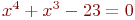 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,97695
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
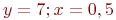 . В ответе указать значение
. В ответе указать значение  после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,981
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
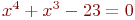 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 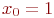 . В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00067
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,027
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,00000002
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
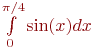 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0001
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
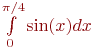 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
386
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000001630
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность величины
. Найти относительную погрешность величины ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины 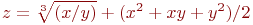 .
.
 | 0,1 |
 | 0,2 |
 | 4 |
 | 5 |
0,065
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
-0,435546875
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 5 | 5 | 7 | 1 | 6 | 68 | |
| 3 | 1 | 5 | 2 | 4 | 48 | |
| 2 | 4 | 3 | 2 | 3 | 44 | |
| 5 | 2 | 2 | 4 | 2 | 55 | |
| 2 | 3 | 6 | 3 | 1 | 41 |
816
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 5-го знака после запятой (без округления).
| 5 | 5 | 7 | 1 | 6 |
| 3 | 1 | 5 | 2 | 4 |
| 2 | 4 | 3 | 2 | 3 |
| 5 | 2 | 2 | 4 | 2 |
| 2 | 3 | 6 | 3 | 1 |
0,00122
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 3 |
 | 2 |
 | 1 |
 | 6 |
 | 0 |
| 5 | 5 | 7 | 1 | 6 | 68 | |
| 3 | 1 | 5 | 2 | 4 | 48 | |
| 2 | 4 | 3 | 2 | 3 | 44 | |
| 5 | 2 | 2 | 4 | 2 | 55 | |
| 2 | 3 | 6 | 3 | 1 | 41 |
17
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 1 | -20 | 150 | -520 | 809 | -420 | 7 |
20
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
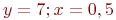 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,408
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
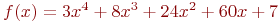 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
9121781
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
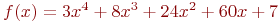 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-40,831899
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
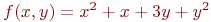 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-0,6;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,50
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
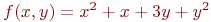 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-1,4;0,5). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,50
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0035
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
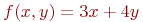 .
Имеется условие:
.
Имеется условие:
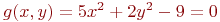 .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
(1) (-9,391) и (9,391)
(2) (-1,359) и (1,359)
(3) (-0,197) и (0,197)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 2 | 2 | 1 | 0 | 30 |
| 0 | 8 | 6 | 0 | 1 | 80 |
| 1 | -2 | -6 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10/3 | 0 | 12 | 20 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 0 | 0 | 16 | 80 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 40/3 | 10/3 | 0 | 80 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,665
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,6911
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,59375. Чему равно
равна 1,59375. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,59375. Чему равно
равна 1,59375. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,1
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 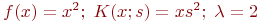 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,8639
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 8 |
| 2 | 43 |
| 3 | 85 |
| 4 | 167 |
| 5 | 259 |
| 6 | 354 |
| 7 | 501 |
| 8 | 630 |
| 9 | 819 |
| 10 | 1016 |
| 11 | 1220 |
| 12 | 1456 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
5,984
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом наступят серьёзные осложнения. Какова вероятность того, что осложнений не будет? Ответ округлите до 3-го знака после запятой (без округления).
0,998
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-7,716
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
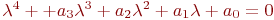 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 1 | 4 | 2 | 2 |
| 3 | 5 | 1 | 9 |
| 5 | 7 | 3 | 7 |
| 2 | 6 | 6 | 5 |
 .
.
70
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
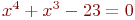 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00202
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,424
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
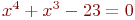 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 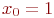 . В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке шестого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
42,62998
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,002
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
0,000000121
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
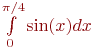 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0003
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
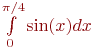 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
9336
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000005215
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
0,05
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,5
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 2 | 4 | 14 | |
| 3 | 5 | 18 |
4
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
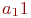 .
.
| 2 | 4 |
| 3 | 5 |
5
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 3 |
| 2 | 4 | 14 | |
| 3 | 5 | 18 |
4
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -8 | 12 | 6 |
-1
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
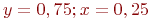 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,706
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
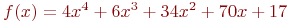 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
-264
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
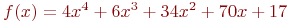 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,045997
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
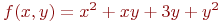 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
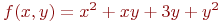 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,50
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,078
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
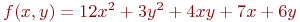 .
Имеется условие:
.
Имеется условие:
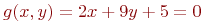 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
(1) f=41; g=17
(2) f=143; g=22
(3) f=131; g=36
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 96 |
| 1 | -4 | -8 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 60 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 16 | 80 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 0 | 25 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,947
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
5,4325
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 2. Чему равно
равна 2. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
5,0
Численно решить интегральное уравнение: ![math]() , где
, где
![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где
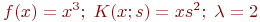 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0033
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 12 |
| 2 | 22 |
| 3 | 31 |
| 4 | 30 |
| 5 | 43 |
| 6 | 62 |
| 7 | 65 |
| 8 | 72 |
| 9 | 87 |
| 10 | 94 |
| 11 | 102 |
| 12 | 120 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
9,524
В урне 5 белых и 6 черных шаров. Из урны вынимают шар и возвращают его в урну. Потом вынимают ещё один раз шар. Найти вероятность того, что оба шара будут белыми.
(1) 2/11
(2) 25/121
(3) 3/11
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,094
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
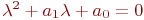 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 1 | 6 |
| 7 | 3 |
 .
.
4
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
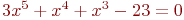 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,375
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,078
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
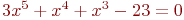 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,15290
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,452
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
0,000000096
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
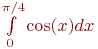 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0008
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
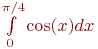 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
823
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000104
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
0,06
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
-0,5
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | 1 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
16
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
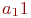 .
.
| 1 | 1 | 2 |
| 5 | 1 | 3 |
| 2 | 4 | 2 |
-10
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 6 |
 | 3 |
| 1 | 1 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
16
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -16 | 76 | -96 | 8 |
5
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
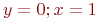 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,7199
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
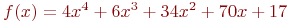 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
19351415010
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
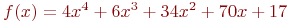 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-21,098368
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
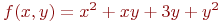 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
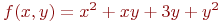 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,43
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0024
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти при каких значениях
.
Найти при каких значениях ![math]() и
и ![math]() достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
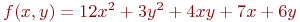 .
Имеется условие:
.
Имеется условие:
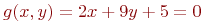 .
Найти при каких значениях
.
Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (0,037;0,222)
(2) (-1,030;-0,424)
(3) (-0,185;-0,514)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 10 |
| 0 | 6 | 5 | 0 | 1 | 96 |
| 1 | -1 | -7 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 90 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 46 | 70 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 20 | 35 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,197
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
6,1723
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1. Чему равно
равна 1. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,3
Численно решить интегральное уравнение: ![math]() , где
, где
![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где
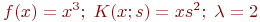 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0174
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 12 |
| 2 | 22 |
| 3 | 31 |
| 4 | 30 |
| 5 | 43 |
| 6 | 62 |
| 7 | 65 |
| 8 | 72 |
| 9 | 87 |
| 10 | 94 |
| 11 | 102 |
| 12 | 120 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,242
В урне 5 белых и 6 черных шаров. Из урны вынимаются сразу два шара. Найти вероятность того, что эти шары будут одного цвета.
(1) 5/121
(2) 1/20
(3) 5/11
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,008
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
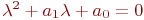 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 1 | 6 |
| 7 | 3 |
 .
.
39
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
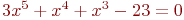 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,75
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
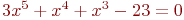 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,75
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
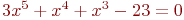 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
-13,59004
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,093
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000205
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
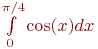 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0009
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
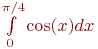 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
1595
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000017
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность 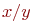 .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
0,11
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
-1,0
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 3 | 2 | 4 | 3 | 38 | |
| 1 | 3 | 5 | 4 | 48 | |
| 1 | 4 | 4 | 2 | 35 | |
| 2 | 3 | 3 | 3 | 38 |
13
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
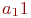 .
.
| 3 | 2 | 4 | 3 |
| 1 | 3 | 5 | 4 |
| 1 | 4 | 4 | 2 |
| 2 | 3 | 3 | 3 |
-12
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 3 |
 | 2 |
 | 7 |
| 3 | 2 | 4 | 3 | 38 | |
| 1 | 3 | 5 | 4 | 48 | |
| 1 | 4 | 4 | 2 | 35 | |
| 2 | 3 | 3 | 3 | 38 |
13
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -17 | 92 | -172 | 96 | 8 |
0
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
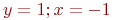 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,876
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
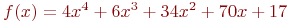 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
93
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
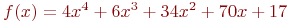 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,045222
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
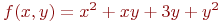 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,4
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
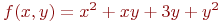 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,89
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,11
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
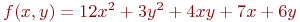 .
Имеется условие:
.
Имеется условие:
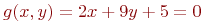 .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
(1) 0,370
(2) -4,788
(3) -2,796
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 1 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 4 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 7 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,715
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
7,2593
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5. Чему равно
равна 1,5. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,2
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 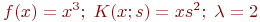 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0483
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 12 |
| 2 | 22 |
| 3 | 31 |
| 4 | 30 |
| 5 | 43 |
| 6 | 62 |
| 7 | 65 |
| 8 | 72 |
| 9 | 87 |
| 10 | 94 |
| 11 | 102 |
| 12 | 120 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
9,444
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью ни из одной урны не были извлечены 2 белых шара?
(1) 17/45
(2) 28/45
(3) 16/45
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,190
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
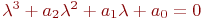 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 4 | 5 | 6 |
| 1 | 7 | 5 |
| 3 | 9 | 8 |
 .
.
19
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
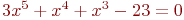 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 1-го знака после запятой (без округления).
14,7
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,880
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
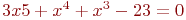 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,39157
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,880
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
0,000000008
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
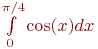 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000001
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
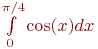 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
386
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000062
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 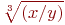 .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
0,034
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
-0,5
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | 2 | 3 | 2 | 1 | 39 | |
| 3 | 6 | 4 | 1 | 2 | 61 | |
| 2 | 3 | 2 | 6 | 2 | 76 | |
| 3 | 6 | 3 | 3 | 3 | 75 | |
| 1 | 2 | 3 | 4 | 2 | 56 |
19
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
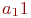 .
.
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
57
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 6 |
 | 3 |
 | 8 |
 | 1 |
| 1 | 2 | 3 | 2 | 1 | 39 | |
| 3 | 6 | 4 | 1 | 2 | 61 | |
| 2 | 3 | 2 | 6 | 2 | 76 | |
| 3 | 6 | 3 | 3 | 3 | 75 | |
| 1 | 2 | 3 | 4 | 2 | 56 |
19
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 1 | -24 | 211 | -816 | 1300 | -672 | 2 |
0
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
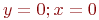 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0003
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
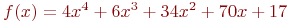 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
307324432
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
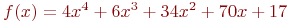 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-21,098145
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
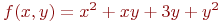 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
-1,0
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
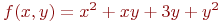 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,90
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0034
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
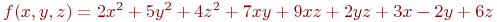 .
Имеется условие:
.
Имеется условие:
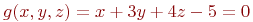 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
(1) f=634; g=40
(2) f=419; g=22
(3) f=385; g=44
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 4 | 4 | 1 | 0 | 0 | 10 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 140 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2,5 | 0 | 0 | 42 | 52,5 | 20 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
4,398
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
8,1421
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,75. Чему равно
равна 1,75. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,6
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 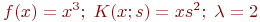 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,1018
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 12 |
| 2 | 22 |
| 3 | 31 |
| 4 | 30 |
| 5 | 43 |
| 6 | 62 |
| 7 | 65 |
| 8 | 72 |
| 9 | 87 |
| 10 | 94 |
| 11 | 102 |
| 12 | 120 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,277
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 2 орла и не более 5-ти очков на игральной кости?
(1) 1/8
(2) 1/4
(3) 3/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,060
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
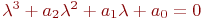 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 4 | 5 | 6 |
| 1 | 7 | 5 |
| 3 | 9 | 8 |
 .
.
48
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
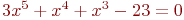 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,375
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
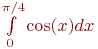 методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000003
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
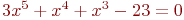 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
-0,90032
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,010
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 9-го знака после запятой (без округления).
0,000000007
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
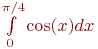 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000002
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
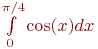 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
2971
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000086
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 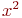 .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
1,6
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,5
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 2 | 4 | 14 | |
| 3 | 5 | 18 |
-2
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 3-го знака после запятой (без округления).
| 2 | 4 |
| 3 | 5 |
-0,500
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 1 |
 | 0 |
| 2 | 4 | 14 | |
| 3 | 5 | 18 |
4
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -8 | 12 | 6 |
8
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
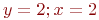 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,183
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
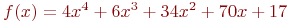 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
-11
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
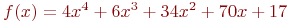 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,045518
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
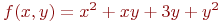 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,64
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
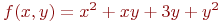 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,29
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
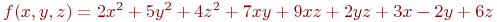 .
Имеется условие:
.
Имеется условие:
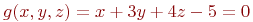 .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (-4,807;-1035;10,053)
(2) (84,640;-8,200;-13,760)
(3) (-7,241;-4,517;5,655)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 3 | 5 | 4 | 1 | 0 | 0 | 25 |
| 0 | 2 | 12 | 6 | 0 | 1 | 0 | 72 |
| 0 | 5 | 35 | 1 | 0 | 0 | 1 | 280 |
| 1 | -3 | -8 | -2 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
14,022
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5191
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,625. Чему равно
равна 1,625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,4
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 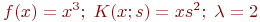 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,1842
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать коэффициенты эмпирической формулы ![math]() методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений ![math]() относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 12 |
| 2 | 22 |
| 3 | 31 |
| 4 | 30 |
| 5 | 43 |
| 6 | 62 |
| 7 | 65 |
| 8 | 72 |
| 9 | 87 |
| 10 | 94 |
| 11 | 102 |
| 12 | 120 |
 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,017
Вероятность выпадения дождя 3/4. Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку в день экзамена 1/2. С какой вероятностью придётся мокнуть под дождём на платформе в хорошем настроении, вызванном положительной оценкой на экзамене?
(1) 3/32
(2) 9/32
(3) 3/8
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,142
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
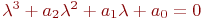 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 4 | 5 | 6 |
| 1 | 7 | 5 |
| 3 | 9 | 8 |
 .
.
7
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
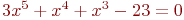 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
1,421875
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000010
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
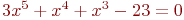 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 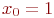 . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
-18
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,401
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000731
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
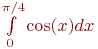 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,12
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
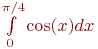 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
823
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000105
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 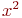 .
.
 | 0,6 |
 | 0,3 |
 | 4 |
 | 5 |
4,8
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
1,0
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | 1 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
22
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 1 | 1 | 2 |
| 5 | 1 | 3 |
| 2 | 4 | 2 |
0,0454
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 7 |
 | 6 |
 | 0 |
| 1 | 1 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
16
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -16 | 76 | -96 | 8 |
16
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
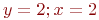 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,0576
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
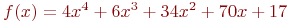 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
55980
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
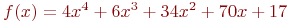 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-21,098236
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
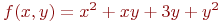 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,30
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
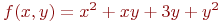 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,015
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
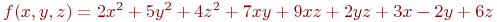 .
Имеется условие:
.
Имеется условие:
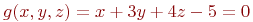 .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
(1) 57,526
(2) 494,680
(3) -98,172
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 7 | 1 | 1 | 0 | 10 |
| 0 | 4 | 2 | 0 | 1 | 40 |
| 1 | -2 | -8 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 10 | 60 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 15 | 0 | 16 | 60 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 20 | 80 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
3,808
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9178
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5625. Чему равно
равна 1,5625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,3
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 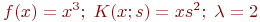 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,3012
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 7 |
| 2 | 47 |
| 3 | 80 |
| 4 | 170 |
| 5 | 250 |
| 6 | 350 |
| 7 | 512 |
| 8 | 620 |
| 9 | 800 |
| 10 | 1024 |
| 11 | 1227 |
| 12 | 1468 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,617
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа компьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью для обеспечения посадки достаточно будет провести ремонт двигателя? Ответ введите с точностью до 3-го знака после запятой (без округления).
0,028
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,020
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
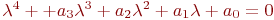 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 6 | 7 | 8 |
| 3 | 9 | 5 | 2 |
| 8 | 2 | 3 | 1 |
| 3 | 4 | 8 | 2 |
 .
.
16
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
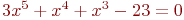 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,395
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | 1 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
22
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
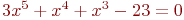 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 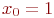 . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
22
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,074
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,00000001
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
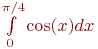 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,12
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
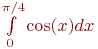 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
1595
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000197
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины 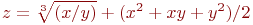 .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
3,3
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
-0,5
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 3 | 2 | 4 | 3 | 38 | |
| 1 | 3 | 5 | 4 | 48 | |
| 1 | 4 | 4 | 2 | 35 | |
| 2 | 3 | 3 | 3 | 38 |
-32
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 3 | 2 | 4 | 3 |
| 1 | 3 | 5 | 4 |
| 1 | 4 | 4 | 2 |
| 2 | 3 | 3 | 3 |
-0,0312
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 1 |
 | 3 |
 | 2 |
 | 0 |
| 3 | 2 | 4 | 3 | 38 | |
| 1 | 3 | 5 | 4 | 48 | |
| 1 | 4 | 4 | 2 | 35 | |
| 2 | 3 | 3 | 3 | 38 |
13
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -17 | 92 | -172 | 96 | 8 |
17
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
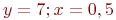 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,886
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
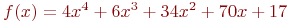 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
41
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
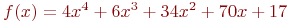 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,045518
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
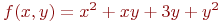 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,99
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
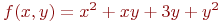 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,41
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
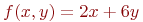 .
Имеется условие:
.
Имеется условие:
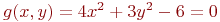 .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
(1) (-0,575;-1,917) и (-0,575;-1,917)
(2) (-0,339;-1,358) и (0,339;1,358)
(3) (-0,197;-1,834) и (0,197;1,834)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 20 |
| 0 | 6 | 1 | 1 | 0 | 1 | 0 | 60 |
| 0 | 2 | 4 | 1 | 0 | 0 | 1 | 140 |
| 1 | -6 | -8 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 10 | 0 | 0 | 0 | 0 | 120 | 60 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 0 | 20 | 60 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 10 | 10 | 0 | 0 | 20 | 80 | 60 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
7,973
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9186
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,6. Чему равно
равна 1,6. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,4
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 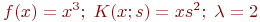 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,4590
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 7 |
| 2 | 47 |
| 3 | 80 |
| 4 | 170 |
| 5 | 250 |
| 6 | 350 |
| 7 | 512 |
| 8 | 620 |
| 9 | 800 |
| 10 | 1024 |
| 11 | 1227 |
| 12 | 1468 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-6,304
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы был Тибальд родственник Монтекки. Если бы не он всё обошлось бы без крови. "Ромео и Джульетта" Шекспира была бы не трагедией, а мелодрамой с хорошим концом. С какой вероятностью это случилось бы?
(1) 1/2
(2) 1/8
(3) 1/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,290
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
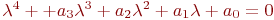 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 6 | 7 | 8 |
| 3 | 9 | 5 | 2 |
| 8 | 2 | 3 | 1 |
| 3 | 4 | 8 | 2 |
 .
.
45
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
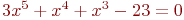 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,40365
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
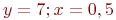 . В ответе указать значение
. В ответе указать значение  после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после десяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,013
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
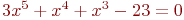 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 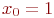 . В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00004
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,013
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,00000004
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
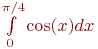 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0001
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
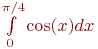 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
386
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000002397
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность величины
. Найти относительную погрешность величины ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины 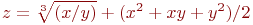 .
.
 | 0,2 |
 | 0,3 |
 | 4 |
 | 5 |
0,10
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
-0,5
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | 2 | 3 | 2 | 1 | 39 | |
| 3 | 6 | 4 | 1 | 2 | 61 | |
| 2 | 3 | 2 | 6 | 2 | 76 | |
| 3 | 6 | 3 | 3 | 3 | 75 | |
| 1 | 2 | 3 | 4 | 2 | 65 |
-3
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 3-го знака после запятой (без округления).
| 1 | 2 | 3 | 2 | 1 |
| 3 | 6 | 4 | 1 | 2 |
| 2 | 3 | 2 | 6 | 2 |
| 3 | 6 | 3 | 3 | 3 |
| 1 | 2 | 3 | 4 | 2 |
-0,333
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 1 |
 | 6 |
 | 3 |
 | 8 |
 | 0 |
| 1 | 2 | 3 | 2 | 1 | 39 | |
| 3 | 6 | 4 | 1 | 2 | 61 | |
| 2 | 3 | 2 | 6 | 2 | 76 | |
| 3 | 6 | 3 | 3 | 3 | 75 | |
| 1 | 2 | 3 | 4 | 2 | 56 |
19
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 1 | -24 | 211 | -816 | 1300 | -672 | 2 |
24
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
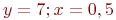 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,091
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
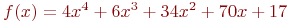 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
11842350
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
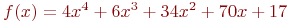 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-21,098236
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
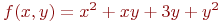 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (0,4;-1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-2,00
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
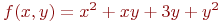 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (0,5;-1,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,021
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
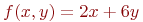 .
Имеется условие:
.
Имеется условие:
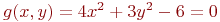 .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
(1) (-0,575) и (0,575)
(2) (-8,831) и (8,831)
(3) (-1,834) и (1,834)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 6 | 4 | 1 | 0 | 10 |
| 0 | 4 | 8 | 0 | 1 | 40 |
| 1 | -4 | -8 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 10 | 20 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 2.5 | 0 | 20 | 20 |
(3)
| X1 | X2 | X3 | X4 | P |
| 2.5 | 5.5 | 0 | 0 | 25 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,847
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9187
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,6125. Чему равно
равна 1,6125. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,3
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 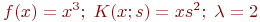 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,6635
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 7 |
| 2 | 47 |
| 3 | 80 |
| 4 | 170 |
| 5 | 250 |
| 6 | 350 |
| 7 | 512 |
| 8 | 620 |
| 9 | 800 |
| 10 | 1024 |
| 11 | 1227 |
| 12 | 1468 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
12,132
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом возможны серьёзные осложнения. Какова вероятность заболевания без осложнений? Ответ округлите до 3-го знака после запятой (без округления).
0,002
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,146
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
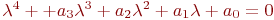 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 6 | 7 | 8 |
| 3 | 9 | 5 | 2 |
| 8 | 2 | 3 | 1 |
| 3 | 4 | 8 | 2 |
 .
.
7
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
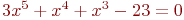 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
-0,00606
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,557
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
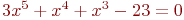 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 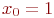 . В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке пятого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
75,21733
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,001
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 7-го знака после запятой (без округления).
0,0000004
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
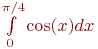 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0003
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
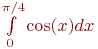 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
2971
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000010320
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
0,075
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,75
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 3 | 6 | 9 | |
| 1 | 7 | -2 |
4
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
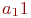 .
.
| 3 | 6 |
| 1 | 7 |
7
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | -1 |
| 3 | 6 | 9 | |
| 1 | 7 | -2 |
4
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -12 | 35 | 7 |
-4
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
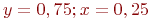 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,7061
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
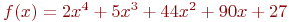 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
-264
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
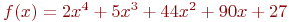 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,103931
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
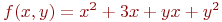 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
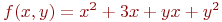 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,47
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,18
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
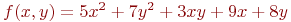 .
Имеется условие:
.
Имеется условие:
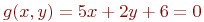 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (2;3).
(1) f=41; g=17
(2) f=143; g=22
(3) f=131; g=36
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 4 | 1 | 1 | 0 | 5 |
| 0 | 2 | 9 | 0 | 1 | 45 |
| 1 | -4 | -5 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 60 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 16 | 80 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 0 | 25 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,728
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9271
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 2. Чему равно
равна 2. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. Чему равно
равна 2. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,6
Численно решить интегральное уравнение: ![math]() , где
, где
![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где
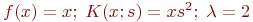 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,1). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,1055
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 28 |
| 2 | 35 |
| 3 | 25 |
| 4 | 55 |
| 5 | 64 |
| 6 | 76 |
| 7 | 83 |
| 8 | 90 |
| 9 | 108 |
| 10 | 117 |
| 11 | 123 |
| 12 | 140 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,552
В урне 5 белых и 6 черных шаров. Из урны вынимают два шара. Потом возвращают их в в урну и вынимают ещё один раз шар. Найти вероятность того, что все три шара будут белыми.
(1) 5/33
(2) 25/121
(3) 3/11
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,094
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
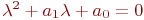 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 4 | 1 |
| 7 | 8 |
 .
.
12
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
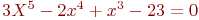 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,375
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,18
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
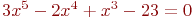 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 11-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,23584
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,278
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 1-го знака после запятой (без округления).
8,41
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
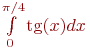 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0030
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
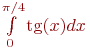 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
287
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000274
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 2-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность  .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
0,02
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,125
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 3 | 7 | 6 | 87 | |
| 1 | 4 | 5 | 58 | |
| 4 | 6 | 8 | 106 |
17
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
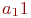 .
.
| 3 | 7 | 6 |
| 1 | 4 | 5 |
| 4 | 6 | 8 |
2
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 3 |
 | 8 |
| 3 | 7 | 6 | 87 | |
| 1 | 4 | 5 | 58 | |
| 4 | 6 | 8 | 106 |
17
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -16 | 83 | -140 | 4 |
24
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
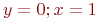 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5092
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
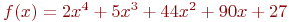 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
на левой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите с точностью до 3-го знака после запятой.
9640734894
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
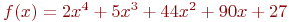 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-22,488910
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
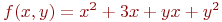 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 5-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
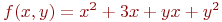 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 10-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,60
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,010
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти при каких значениях
.
Найти при каких значениях ![math]() и
и ![math]() достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
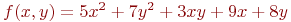 .
Имеется условие:
.
Имеется условие:
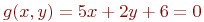 .
Найти при каких значениях
.
Найти при каких значениях  и
и  достигается условный экстремум. Ответ — с точностью до 3-го знака.
достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (0,037;0,222)
(2) (-1,030;-0,424)
(3) (-0,186;-0,514)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 3 | 1 | 1 | 0 | 5 |
| 0 | 6 | 5 | 0 | 1 | 45 |
| 1 | -3 | -7 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 12 | 90 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 10 | 0 | 46 | 70 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 0 | 20 | 35 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,784
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9271
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1. Чему равно
равна 1. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. Чему равно
равна 1. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
2,9
Численно решить интегральное уравнение: ![math]() , где
, где
![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где
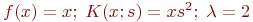 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,2). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,2220
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом наименьших квадратов эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 28 |
| 2 | 35 |
| 3 | 25 |
| 4 | 55 |
| 5 | 64 |
| 6 | 76 |
| 7 | 83 |
| 8 | 90 |
| 9 | 108 |
| 10 | 117 |
| 11 | 123 |
| 12 | 140 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,076
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,995
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
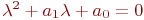 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 4 | 1 |
| 7 | 8 |
 .
.
25
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
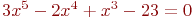 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,75
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
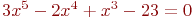 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,75
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
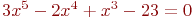 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 11-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
-17,12934
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,076
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,622
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
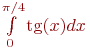 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0030
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
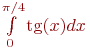 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
363
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000043
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность
. Найти относительную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность
. Найти относительную погрешность 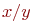 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
0,095
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
-0,5625
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 4 | 1 | 3 | 4 | 43 | |
| 3 | 2 | 1 | 2 | 31 | |
| 1 | 2 | 5 | 3 | 38 | |
| 2 | 3 | 4 | 1 | 34 |
15
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
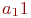 .
.
| 4 | 1 | 3 | 4 |
| 3 | 2 | 1 | 2 |
| 1 | 2 | 5 | 3 |
| 2 | 3 | 4 | 1 |
-21
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 5 |
 | 2 |
 | 5 |
| 4 | 1 | 3 | 4 | 43 | |
| 3 | 2 | 1 | 2 | 31 | |
| 1 | 2 | 5 | 3 | 38 | |
| 2 | 3 | 4 | 1 | 34 |
15
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -17 | 99 | -223 | 140 | 1 |
-72
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
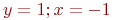 . В ответе указать значение
. В ответе указать значение  после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после шести итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,496
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
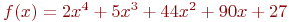 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
93
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
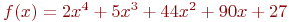 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,102906
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
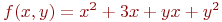 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
-1,0
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
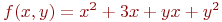 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,91
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 2-го знака после запятой (без округления).
. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,20
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
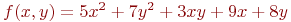 .
Имеется условие:
.
Имеется условие:
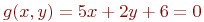 .
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
.
Найти значение условного экстремума. Ответ — с точностью до 3-го знака.
(1) 0,370
(2) -4,788
(3) -2,796
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 1 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 4,5 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 8 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 12 | 80 | 90 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 32 | 70 | 80 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10 | 0 | 0 | 36 | 80 | 90 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,850
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9272
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5. Чему равно
равна 1,5. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. Чему равно
равна 1,5. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,7
Численно решить интегральное уравнение: ![math]() , где
, где
![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где
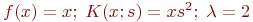 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,3). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,3495
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 28 |
| 2 | 35 |
| 3 | 25 |
| 4 | 55 |
| 5 | 64 |
| 6 | 76 |
| 7 | 83 |
| 8 | 90 |
| 9 | 108 |
| 10 | 117 |
| 11 | 123 |
| 12 | 140 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,500
В первой урне 3 белых шара и 7 чёрных. Во второй урне 6 белых и 4 чёрных. Из обеих урн вынимают по 2 шара. С какой вероятностью только из одной урны извлечены 2 белых шара?
(1) 17/45
(2) 28/45
(3) 16/45
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,094
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
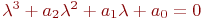 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 5 | 2 |
| 1 | 3 | 9 |
| 2 | 7 | 6 |
 .
.
12
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
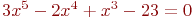 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 3-х делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
-3,16
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,525
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
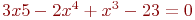 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать координату 66-той точки сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,59649
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение многочлена в точке
. В ответе привести значение многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,525
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,15
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
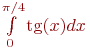 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000001
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
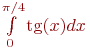 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
38
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000035
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 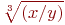 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
0,029
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 5-го знака после запятой (без округления).
. Ответ введите с точностью до 5-го знака после запятой (без округления).
-0,96875
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней.
| 1 | -1 | 3 | 1 | 5 | |
| 4 | -1 | 5 | 4 | 4 | |
| 2 | -2 | 4 | 1 | 6 | |
| 1 | -4 | 5 | -1 | 3 |
21
Дана квадратная матрица. Найти значение алгебраического дополнения элемента ![math]() .
.
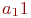 .
.
| 2 | 4 | 3 | 3 | 2 |
| 2 | 5 | 3 | 1 | 2 |
| 1 | 4 | 1 | 4 | 3 |
| 2 | 3 | 2 | 5 | 6 |
| 1 | 4 | 5 | 6 | 8 |
84
Решить методом Гаусса систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 0 |
 | 0 |
| 4 | 1 | -1 | 3 | |
| 2 | -2 | 1 | 1 | |
| 1 | -1 | 2 | 5 |
6
Дан многочлен ![math]() . Разделить его на многочлен
. Разделить его на многочлен ![math]() . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 . Разделить его на многочлен
. Разделить его на многочлен  . Сумму коэффициентов получившегося многочлена записать в ответ.
. Сумму коэффициентов получившегося многочлена записать в ответ.
 |  |  |  |  |  |  |
| 1 | -24 | 218 | -916 | 1701 | -980 | 1 |
432
Организовать поиск решения системы уравнений методом простой итерации.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
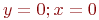 . В ответе указать значение
. В ответе указать значение  после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после трёх итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
5,029
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
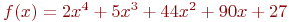 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 4-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
155522583
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
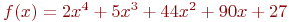 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 30-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-22,488485
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
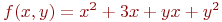 методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,1. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 20-ти циклов. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,4
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
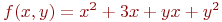 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (1;1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 25-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,91
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,011
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
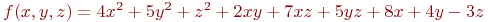 .
Имеется условие:
.
Имеется условие:
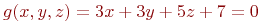 .
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
.
Вычислить значение функции (округлить до целых) и проверить: выполняется ли условие в точке (4;5;2).
(1) f=634; g=40
(2) f=419; g=22
(3) f=385; g=44
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 5 | 3 | 1 | 0 | 0 | 10 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2,5 | 0 | 0 | 42 | 52,5 | 20 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 2 | 0 | 0 | 63 | 128 | 18 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,910
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,9272
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,75. Чему равно
равна 1,75. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. Чему равно
равна 1,75. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,2
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 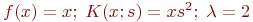 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,4). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,4881
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 28 |
| 2 | 35 |
| 3 | 25 |
| 4 | 55 |
| 5 | 64 |
| 6 | 76 |
| 7 | 83 |
| 8 | 90 |
| 9 | 108 |
| 10 | 117 |
| 11 | 123 |
| 12 | 140 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,416
Подброшены три монеты и игральная кость. С какой вероятностью выпадет 1 орёл и не более 4-х очков на игральной кости?
(1) 1/8
(2) 1/4
(3) 3/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,996
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
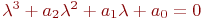 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 5 | 2 |
| 1 | 3 | 9 |
| 2 | 7 | 6 |
 .
.
27
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
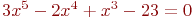 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать левую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5625
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
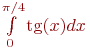 методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 100 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000005
Задано уравнение ![math]() ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
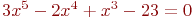 ; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом хорд на отрезке [1;4]. В ответе указать значение левой части уравнения в 66-той точке сечения отрезка хордой. Ответ введите с точностью до 5-го знака после запятой (без округления).
-0,80941
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,016
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0794
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
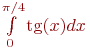 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать абсолютную величину разности между истинным значением интеграла и расчётным. Ответ введите с точностью до 6-го знака после запятой (без округления).
0,000003
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
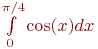 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз абсолютная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
726
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000021
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 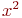 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
2,4
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 6-го знака после запятой (без округления).
. Ответ введите с точностью до 6-го знака после запятой (без округления).
-0,890625
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 3 | 6 | 9 | |
| 1 | 7 | -2 |
15
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 3 | 6 |
| 1 | 7 |
-0,0666
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 5 |
 | 0 |
| 3 | 6 | 9 | |
| 1 | 7 | -2 |
4
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | -12 | 35 | 7 |
12
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
 |
 |
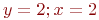 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 4-го знака после запятой (без округления).
2,1831
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
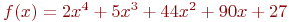 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
-11
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
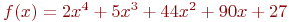 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,103298
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
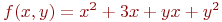 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,30
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
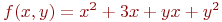 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,97
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,5
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
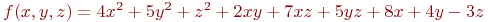 .
Имеется условие:
.
Имеется условие:
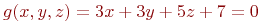 .
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
.
Найти в какой точке достигается условный экстремум. Ответ — с точностью до 3-го знака.
(1) (-4,807;-1035;10,053)
(2) (52,160;-5,80;-7,440)
(3) (0,543;0,413;-1,974)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 4 | 9 | 3 | 1 | 0 | 0 | 27 |
| 0 | 6 | 9 | 2 | 0 | 1 | 0 | 81 |
| 0 | 1 | 16 | 5 | 0 | 0 | 1 | 160 |
| 1 | -4 | -9 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 80 | 45 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 5 | 0 | 0 | 12 | 105 | 40 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 3 | 0 | 0 | 54 | 112 | 27 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
3,340
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,3670
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,625. Чему равно
равна 1,625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. Чему равно
равна 1,625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
4,0
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 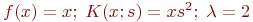 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,5). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,6376
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать коэффициенты эмпирической формулы ![math]() методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений ![math]() относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 28 |
| 2 | 35 |
| 3 | 25 |
| 4 | 55 |
| 5 | 64 |
| 6 | 76 |
| 7 | 83 |
| 8 | 90 |
| 9 | 108 |
| 10 | 117 |
| 11 | 123 |
| 12 | 140 |
 методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений
методом средних и методом наименьших квадратов. В ответе во сколько раз дисперсия значений  относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
относительно зависимости полученной методом средних больше, чем дисперсия относительно зависимости полученной методом наименьших квадратов. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,000
Вероятность получения положительной оценки на экзамене 3/4. Вероятность опоздания на последнюю электричку вдень экзамена 1/2. С какой вероятностью всё будет хорошо?
(1) 3/32
(2) 9/32
(3) 3/8
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,140
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
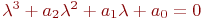 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 3 | 5 | 2 |
| 1 | 3 | 9 |
| 2 | 7 | 6 |
 .
.
73
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
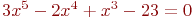 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать правую границу отрезка полученного после 6-ти делений. Ответ введите с точностью до 6-го знака после запятой (без округления).
1,609375
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 10-го знака после запятой (без округления).
0,0000000003
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
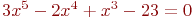 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 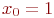 . В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение левой части уравнения в точке нулевого приближения (целое число).
-21
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,257
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,067
Вычислить значение интеграла ![math]() методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
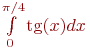 методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "левых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
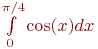 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "левых" прямоугольников. Ответ округлить до целых.
287
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000024
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность
. Найти абсолютную погрешность ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность
. Найти абсолютную погрешность 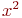 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
2,4
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 7-го знака после запятой (без округления).
. Ответ введите с точностью до 7-го знака после запятой (без округления).
-0,3671875
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 3 | 7 | 6 | 87 | |
| 1 | 4 | 5 | 58 | |
| 4 | 6 | 8 | 106 |
30
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 3 | 7 | 6 |
| 1 | 4 | 5 |
| 4 | 6 | 8 |
0,0333
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 6 |
 | 3 |
 | 0 |
| 3 | 7 | 6 | 87 | |
| 1 | 4 | 5 | 58 | |
| 4 | 6 | 8 | 106 |
17
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 0 | 1 | -16 | 83 | -140 | 4 |
16
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
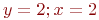 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,057
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
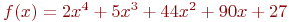 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на левой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
27989
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
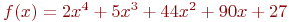 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на левой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-22,488658
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
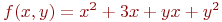 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 30-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,65
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
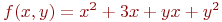 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 40 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,97
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти абсолютную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,048
Задана функция трёх переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
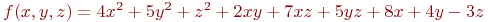 .
Имеется условие:
.
Имеется условие:
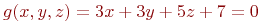 .
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
.
Найти значение функции в условным экстремуме. Ответ — с точностью до 3-го знака.
(1) 57,526
(2) 430,36
(3) 6,715
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 5 | 1 | 0 | 20 |
| 0 | 2 | 3 | 0 | 1 | 50 |
| 1 | -4 | -6 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 0 | 15 | 0 | 10 | 40 |
(2)
| X1 | X2 | X3 | X4 | P |
| 0 | 4 | 0 | 38 | 24 |
(3)
| X1 | X2 | X3 | X4 | P |
| 0 | 5 | 10 | 0 | 20 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,220
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5269
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,5625. Чему равно
равна 1,5625. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. Чему равно
равна 1,5625. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,9
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 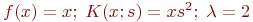 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,6). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,7982
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 18 |
| 2 | 50 |
| 3 | 91 |
| 4 | 169 |
| 5 | 257 |
| 6 | 354 |
| 7 | 524 |
| 8 | 612 |
| 9 | 799 |
| 10 | 1010 |
| 11 | 1212 |
| 12 | 1453 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
10,218
Вероятность отказа бортового компьютера 0,01. Вероятность отказа двигателя 0,03. Вероятность отказа навигационной системы 0,05. После отказа двигателя спутник не сможет сойти с орбиты. В случае отказа к омпьютера или навигационной системы спутник не сможет правильно выбрать место приземления. С какой вероятностью потребуется ремонт только компьютера или только навигационной системы? Ответ введите с точностью до 3-го знака после запятой (без округления).
0,037
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,992
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
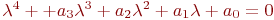 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 3 | 5 | 1 |
| 2 | 5 | 9 | 3 |
| 7 | 3 | 4 | 6 |
| 2 | 4 | 5 | 2 |
 .
.
13
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
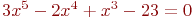 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 6-ти делений. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,56
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 2 | 2 | 2 | 19 | |
| 5 | 1 | 3 | 50 | |
| 2 | 4 | 2 | 44 |
8
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
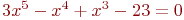 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 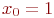 . В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
. В ответе указать значение производной от левой части уравнения в точке нулевого приближения (целое число).
10
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,093
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0962
Вычислить значение интеграла ![math]() методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
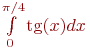 методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
методом "правых" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 1-го знака после запятой (без округления).
0,8
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
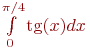 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "правых" прямоугольников. Ответ округлить до целых.
363
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000028
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины ![math]() .
.
Ответ введите с точностью до 1-го знака после запятой (без округления).
 и
и  . Найти абсолютную погрешность величины
. Найти абсолютную погрешность величины 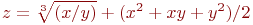 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
2,6
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 8-го знака после запятой (без округления).
. Ответ введите с точностью до 8-го знака после запятой (без округления).
0,33984375
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 4 | 1 | 3 | 4 | 43 | |
| 3 | 2 | 1 | 2 | 31 | |
| 1 | 2 | 5 | 3 | 38 | |
| 2 | 3 | 4 | 1 | 34 |
-55
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 4-го знака после запятой (без округления).
| 4 | 1 | 3 | 4 |
| 3 | 2 | 1 | 2 |
| 1 | 2 | 5 | 3 |
| 2 | 3 | 4 | 1 |
-0,0181
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 3 |
 | 5 |
 | 2 |
 | 0 |
| 4 | 1 | 3 | 4 | 43 | |
| 3 | 2 | 1 | 2 | 31 | |
| 1 | 2 | 5 | 3 | 38 | |
| 2 | 3 | 4 | 1 | 34 |
15
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 0 | 1 | -17 | 99 | -223 | 140 | 1 |
17
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
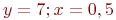 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,971
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
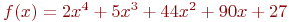 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
41
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
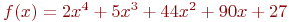 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-1,103298
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
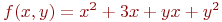 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-2,00
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
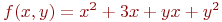 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
-1,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для ![math]() . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только одного члена ряда для  . Ответ введите с точностью до 1-го знака после запятой (без округления).
. Ответ введите с точностью до 1-го знака после запятой (без округления).
1,0
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
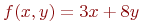 .
Имеется условие:
.
Имеется условие:
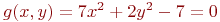 .
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
.
Найти положение условных экстремумов. Ответ — с точностью до 3-го знака.
(1) (-0,575;-1,917) и (-0,575;-1,917)
(2) (-0,340;-1,359) и (0,340;1,359)
(3) (-0,196;-1,834) и (0,196;1,834)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | X5 | X6 | |
| 0 | 2 | 2 | 4 | 1 | 0 | 0 | 30 |
| 0 | 8 | 1 | 1 | 0 | 1 | 0 | 45 |
| 0 | 1 | 4 | 1 | 0 | 0 | 1 | 120 |
| 1 | -8 | -4 | -4 | 0 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 30/7 | 75/7 | 0 | 0 | 0 | 510/7 | 540/7 |
(2)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 0 | 10/7 | 0 | 0 | 36/7 | 70 | 80 |
(3)
| X1 | X2 | X3 | X4 | X5 | X6 | P |
| 30 | 75 | 0 | 0 | 36 | 160 | 90/7 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,335
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5269
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,6. Чему равно
равна 1,6. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. Чему равно
равна 1,6. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,9
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 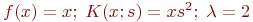 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,7). Ответ введите с точностью до 4-го знака после запятой (без округления).
0,9698
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 18 |
| 2 | 50 |
| 3 | 91 |
| 4 | 169 |
| 5 | 257 |
| 6 | 354 |
| 7 | 524 |
| 8 | 612 |
| 9 | 799 |
| 10 | 1010 |
| 11 | 1212 |
| 12 | 1453 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-3,281
Пусть вероятность рождения мальчика 0,5. Если бы на месте детей Капулетти (Джульетты) и Монтекки (Ромео) оказались однополые дети, то ничего не случилось бы. Важным звеном драмы были друг Ромео Меркуцио и Тибальд родственник Монтекки. Если бы на их месте были бы девочки, то "Ромео и Джульетта" Шекспира была бы не трагедией, а комедией с хорошим концом. С какой вероятностью это случилось бы?
(1) 1/2
(2) 1/8
(3) 1/16
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,140
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
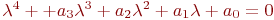 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 3 | 5 | 1 |
| 2 | 5 | 9 | 3 |
| 7 | 3 | 4 | 6 |
| 2 | 4 | 5 | 2 |
 .
.
52
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
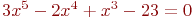 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать координату середины отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
1,60745
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
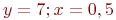 . В ответе указать значение
. В ответе указать значение  после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после двадцати итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,999
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
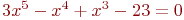 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 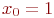 . В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
0,00021
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,171
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,233
Вычислить значение интеграла ![math]() методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
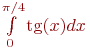 методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом "центральных" прямоугольников. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0004
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
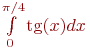 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы трапеций. Ответ округлить до целых.
38
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000069
Даны значения и абсолютные погрешности величин ![math]() и
и ![math]() . Найти относительную погрешность величины
. Найти относительную погрешность величины ![math]() .
.
Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  . Найти относительную погрешность величины
. Найти относительную погрешность величины 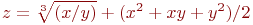 .
.
 | 0,3 |
 | 0,1 |
 | 4 |
 | 5 |
0,084
Вычислить значение многочлена Чебышева степени ![math]() (
(![math]() ) при
) при ![math]() . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
 (
( ) при
) при  . Ответ введите с точностью до 9-го знака после запятой (без округления).
. Ответ введите с точностью до 9-го знака после запятой (без округления).
0,876953125
Вычислить главный определитель системы линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов.
| 1 | -1 | 3 | 1 | 5 | |
| 4 | -1 | 5 | 4 | 4 | |
| 2 | -2 | 4 | 1 | 6 | |
| 1 | -4 | 5 | -1 | 3 |
-3
Дана квадратная матрица. Найти значение определителя обратной матрицы. Ответ введите с точностью до 5-го знака после запятой (без округления).
| 2 | 4 | 3 | 3 | 2 |
| 2 | 5 | 3 | 1 | 2 |
| 1 | 4 | 1 | 4 | 3 |
| 2 | 3 | 2 | 5 | 6 |
| 1 | 4 | 5 | 6 | 8 |
0,00366
Решить методом Гаусса-Зейделя систему линейных алгебраических уравнений заданных матрицей левой части и столбцом свободных членов. В ответе указать сумму корней. В Качестве нулевого приближения использовать значения корней заданных в таблице:
 | 0 |
 | 0 |
 | 0 |
| 4 | 1 | -1 | 3 | |
| 2 | -2 | 1 | 1 | |
| 1 | -1 | 2 | 5 |
6
Дан многочлен ![math]() . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 . Найти его корни. Сумму корней записать в ответ.
. Найти его корни. Сумму корней записать в ответ.
 |  |  |  |  |  |  |
| 1 | -24 | 218 | -916 | 1701 | -980 | 1 |
24
Организовать поиск решения системы уравнений методом Гаусса-Зейделя.
Поиск начать с точки ![math]() . В ответе указать значение
. В ответе указать значение ![math]() после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
 |
 |
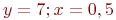 . В ответе указать значение
. В ответе указать значение  после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
после девяти итераций. Ответ введите с точностью до 3-го знака после запятой (без округления).
2,021
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
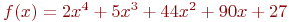 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
на правой границе интервала поиска на 8-м этапе деления отрезка. Ответ введите в виде целого числа без округления.
6107392
Организуйте методом золотого сечения поиск минимума функции ![math]() . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение ![math]() на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
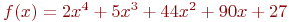 . Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение
. Поиск организуйте на отрезке [-1200;1250]. В ответе укажите значение  на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
на правой границе интервала поиска на 50-м этапе деления отрезка. Ответ введите с точностью до 6-го знака после запятой (без округления).
-22,488658
Организовать процесс поиска минимума функции ![math]() методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по ![math]() и завершается спуском по
и завершается спуском по ![math]() . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
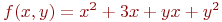 методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по
методом покоординатного спуска. Шагом 0,01. Цикл спуска начинается со спуска по  и завершается спуском по
и завершается спуском по  . Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты
. Производные вычисляются численно. Спуск начать из точки (-1;0,4). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 100 циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,00
Организовать процесс поиска минимума функции ![math]() градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты ![math]() , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
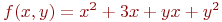 градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты
градиентным методом. Шагом 0,1. Производные вычисляются аналитически. Поиск начать из точки (-0,5;-1,1). В ответе указать значение координаты  , в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
, в которой будет находиться процесс оптимизации после 80-ти циклов. Ответ введите с точностью до 2-го знака после запятой (без округления).
0,99
Разложение функции ![math]() в ряд имеет вид:
в ряд имеет вид: ![math]() . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в ряд имеет вид:
в ряд имеет вид:  . Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для
. Найти относительную погрешность вычислений, возникающую при суммировании только двух членов ряда для  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,096
Задана функция двух переменных:
![math]() .
Имеется условие:
.
Имеется условие:
![math]() .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
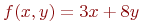 .
Имеется условие:
.
Имеется условие:
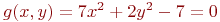 .
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
.
Найти значения функции в условных экстремумах. Ответ — с точностью до 3-го знака.
(1) (-9,391) и (9,391)
(2) (-8,832) и (8,832)
(3) (-15,264) и (15,264)
Дана симплекс таблица. Найти решение.
| P | X1 | X2 | X3 | X4 | |
| 0 | 8 | 2 | 1 | 0 | 25 |
| 0 | 4 | 8 | 0 | 1 | 65 |
| 1 | -6 | -8 | 0 | 0 | 0 |
(1)
| X1 | X2 | X3 | X4 | P |
| 1.25 | 7.5 | 0 | 0 | 67.5 |
(2)
| X1 | X2 | X3 | X4 | P |
| 2.25 | 10 | 0 | 16.5 | 80 |
(3)
| X1 | X2 | X3 | X4 | P |
| 1 | 5 | 2 | 0 | 25 |
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,518
Организовать решение методом Рунге-Кутта дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 4-го знака после запятой (без округления).
. Ответ введите с точностью до 4-го знака после запятой (без округления).
1,5269
Для дифференциального уравнения ![math]() задана краевая задача
задана краевая задача ![math]() . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия: ![math]() ; производная в точке
; производная в точке ![math]() равна 1,6125. Чему равно
равна 1,6125. Чему равно ![math]() . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
 задана краевая задача
задана краевая задача  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. Чему равно
равна 1,6125. Чему равно  . Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
. Шаг решения методом Эйлера 0,1. Ответ введите с точностью до 1-го знака после запятой (без округления).
3,9
Численно решить интегральное уравнение: ![math]() , где
, где ![math]() . Использовать шаг
. Использовать шаг ![math]() . Решение получить на сетке:
. Решение получить на сетке:
Подсказка. Необходимо решить матричное уравнение: ![math]() ; где
; где ![math]() . Где
. Где ![math]() . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
 , где
, где 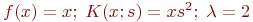 . Использовать шаг
. Использовать шаг  . Решение получить на сетке:
. Решение получить на сетке:
 |
| 0,0 |
| 0,1 |
| 0,2 |
| 0,3 |
| 0,4 |
| 0,5 |
| 0,6 |
| 0,7 |
| 0,8 |
 ; где
; где  . Где
. Где  . Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
. Привести значение y(0,8). Ответ введите с точностью до 4-го знака после запятой (без округления).
1,1524
Заданы значения двенадцати пар ![math]() и
и ![math]() .
.
Подобрать методом средних эмпирическую формулу ![math]() . В ответе указать значение
. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 и
и  .
.
 |  |
| 1 | 18 |
| 2 | 50 |
| 3 | 91 |
| 4 | 169 |
| 5 | 257 |
| 6 | 354 |
| 7 | 524 |
| 8 | 612 |
| 9 | 799 |
| 10 | 1010 |
| 11 | 1212 |
| 12 | 1453 |
 . В ответе указать значение
. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
13,562
Вероятность заразиться гриппом 0,2. Вероятность получить пищевое отравление 0,01. В случае отравления и заболевания гриппом внаступят серьёзные осложнения. Какова вероятность осложнений? Ответ округлите до 3-го знака после запятой (без округления).
0,206
Построить кубический сплайн ![math]() для интерполяции значений функции
для интерполяции значений функции ![math]() на сетке значений
на сетке значений ![math]() . В ответе привести значение
. В ответе привести значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 для интерполяции значений функции
для интерполяции значений функции  на сетке значений
на сетке значений  . В ответе привести значение
. В ответе привести значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
-0,991
Найти абсолютные значения коэффициентов характеристического уравнения ![math]() для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
В ответе указать значение ![math]() .
.
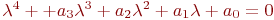 для нахождения собственных значений матрицы:
для нахождения собственных значений матрицы:
| 2 | 3 | 5 | 1 |
| 2 | 5 | 9 | 3 |
| 7 | 3 | 4 | 6 |
| 2 | 4 | 5 | 2 |
 .
.
28
Задано уравнение ![math]() ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
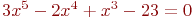 ; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
; организовать его решение методом дихотомии на отрезке [1;4]. В ответе указать значение левой части уравнения в середине отрезка полученного после 14-ти делений. Ответ введите с точностью до 5-го знака после запятой (без округления).
-0,00287
Организовать решение методом Эйлера дифференциального уравнения: ![math]() . Начальные условия
. Начальные условия ![math]() . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
1,332
Задано уравнение ![math]() ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять ![math]() . В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
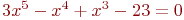 ; организовать его решение касательных. За нулевое приближение принять
; организовать его решение касательных. За нулевое приближение принять 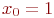 . В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
. В ответе указать значение производной от левой части уравнения в точке седьмого приближения. Ответ введите с точностью до 5-го знака после запятой (без округления).
74,68017
Используя значения функции ![math]() в точках
в точках ![math]() и
и ![math]() построить интерполяционный многочлен
построить интерполяционный многочлен ![math]() . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке ![math]() . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
 в точках
в точках  и
и  построить интерполяционный многочлен
построить интерполяционный многочлен  . В ответе привести разницу между значением функции и значением многочлена в точке
. В ответе привести разницу между значением функции и значением многочлена в точке  . Ответ введите с точностью до 3-го знака после запятой (без округления).
. Ответ введите с точностью до 3-го знака после запятой (без округления).
0,015
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для ![math]() и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке ![math]() , где
, где ![math]() . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Лагранжа для  и вычислить значение многочлена Лагранжа в точке
и вычислить значение многочлена Лагранжа в точке  , где
, где  . В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
. В ответе указать относительную погрешность приближения функции в процентах. Ответ введите с точностью до 2-го знака после запятой (без округления).
1,11
Вычислить значение интеграла ![math]() методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
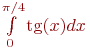 методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
методом трапеций. Интервал интегрирования разбить на 128 участков. В ответе указать модуль относительной погрешности (в процентах) по сравнению с истинным значением интеграла. Ответ введите с точностью до 4-го знака после запятой (без округления).
0,0009
Вычислить значение интеграла ![math]() по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
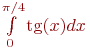 по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
по формуле Симпсона (без разбиения отрезка). В ответе указать во сколько раз относительная погрешность этой формулы меньше чем у формулы "центральных" прямоугольников. Ответ округлить до целых.
726
Дана сетка значений ![math]() , где
, где ![math]() принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для ![math]() и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке ![math]() , где
, где ![math]() . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
 , где
, где  принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для
принимает значения 0; 1; 2; 3; 4; 5; 6; 7; 8. Построить многочлен Ньютона для  и вычислить значение многочлена Ньютона в точке
и вычислить значение многочлена Ньютона в точке  , где
, где  . В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
. В ответе указать абсолютную погрешность приближения функции. Ответ введите с точностью до 11-го знака после запятой (без округления).
0,00000000266