Главная / Экономика / Логистика

Логистика - ответы на тесты Интуит

Правильные ответы выделены зелёным цветом.
Все ответы: Данный курс знакомит с моделями, используемыми в логистике – науке исследующей оптимальные способы управления запасами и их распределение.

Смотрите также:

Менеджмент

Найти оптимальный объем партии с точки зрения минимума расходов на приобретение товаров, если цена товара зависит от объема партии math

как

а стоимость хранения как math

. Ответ округлить до одного знака после запятой.

3,5

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

835

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать общее количество груза экспедируемого в направлении B-I (целое число).

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	8	6	4	6	110
II	2	7	2	3	40
III	5	7	8	3	70
IV	8	5	2	3	50
Наличие	90	40	50	90	270

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1530

(2) 1250

(3) 1060

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 2; 7.

Для производства продукции используются ресурсы трех видов в следующих количествах (первое число относится к первому виду продукции, второе ко второму).

Первый ресурс: 1 и 6.

Второй ресурс: 3 и 1

Третий ресурс: 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти программу производства, приносящую наибольшую прибыль.

(1) продукции первого вида 0 единиц второго вида 6 единиц

(2) продукции первого вида 2 единиц второго вида 0 единиц

(3) продукции первого вида 0 единиц второго вида 7 единиц

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	4	1	1	0	10
0	2	6	0	1	72
1	-3	-6	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	60

(2)

X1	X2	X3	X4	P
0	10	0	16	80

(3)

X1	X2	X3	X4	P
0	5	0	0	25

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение суммы весов. Ответ округлить до двух знаков после запятой.

0,29

Задана продолжительность работ для перевода системы из состояния в состояние. Найти общее минимально возможное время выполнения работы для перевода системы из состояния 0 в конечное состояние (целое число).

Состояние	1	2	3
0	5	3	4
1		2	2
2			4

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	5
	2
	-1
	3
	0,2

Найти равновесный спрос. Ответ введите с точностью до 1-й цифры после запятой.

2,6

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		12

Найти оптимальный размер заказа. Ответ округлить до целых.

224

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1\;5\;4\\
8\;2\;3\\
4\;5\;7
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
52\\
70\\
91\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		12

Найти оптимальный размер заказа. Ответ округлить до целых.

224

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный объем поставки товара А. Ответ округлить до целых.

224

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку средней суточной потребности. Ответ -- целое число.

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

. Учтите, что при сложении и умножении случайных величин полученная случайная величина имеет среднее квадратичное отклонение, определяемое формулой: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,001
	0,999
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика A к потребителю I (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Для составления исходного плана перевозок по методу Фогеля нужно определить разности между двумя минимальными тарифами в каждой строке и столбце. В ответе укажите полученную разность для первой строки (целое число).

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю I (целое число).

Найти величину минимальных расходов на приобретение товаров, если цена товара зависит от объема партии math

как

, а стоимость хранения как math

	-1
	1
	9
	2
	-8
	5

Ответ округлить до двух знаков после запятой.

1,75

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				30
III				40
Наличие	25	40	25	90

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

450

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать общее количество груза экспедируемого в направлении A-II (целое число).

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	8	6	4	6	110
II	2	7	2	3	40
III	5	7	8	3	70
IV	8	5	2	3	50
Наличие	90	40	50	90	270

Найти оптимальный план перевозок и определить его стоимость.

(1) 1100

(2) 930

(3) 820

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 2; 7.

Первый ресурс: 1 и 6.

Второй ресурс: 3 и 1

Третий ресурс: 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти наибольшую прибыль.

(1) 42

(2) 12

(3) 10

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	7	1	1	0	10
0	6	6	0	1	72
1	-4	-9	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	90

(2)

X1	X2	X3	X4	P
0	10	0	46	70

(3)

X1	X2	X3	X4	P
0	5	0	20	35

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего X. Ответ округлить до одного знака после запятой.

3,4

Состояние	1	2	3	4
0	5	3	4
1		2	2	7
2			4	6
3				3

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	5
	2
	-1
	3
	0,2

Найти равновесную цену. Ответ введите с точностью до 1-й цифры после запятой.

1,2

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Цена товара (руб./ед.)	1500

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

310

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
2\;5\;4\\
8\;1\;3\\
4\;4\;7
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
50\\
70\\
90\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		12

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

310

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку дисперсии суточной потребности. Ответ округлить до одного знака после запятой.

8,8

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,001
	0,999
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

999

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю I (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю II (целое число).

Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до двух знаков после запятой.

	-1
	1
	9
	2
	-8
	5

3,39

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				65
III				50
Наличие	35	60	30	125

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

670

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать общее количество груза экспедируемого в направлении B-II (целое число).

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	5	1	2	110
II	7	1	8	6	40
III	6	3	3	7	70
IV	4	2	1	3	50
Наличие	90	40	50	90	270

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1160

(2) 1250

(3) 1440

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 30\\
3X_1+X_2+5X_3 \le 55\\
3X_1+2X_2+X_3 \le 9

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	7	1	2	1	0	0	10
0	6	6	6	0	1	0	72
0	7	8	7	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	12	80	90

(2)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	32	70	80

(3)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	36	80	90

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего квадрата math

. Ответ округлить до двух знаков после запятой.

19,17

Состояние	1	2	3	4	5
0	5	3	4
1		2	2	7
2			4	6	2
3				3	5
4					3

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	5
	2
	-1
	3
	0,2

Найти найти цену предложения, при которой товарооборот максимален. Ответ введите с точностью до 2-й цифры после запятой.

1,25

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку среднего квадратичного отклонения суточной потребности. Ответ округлить до двух знаков после запятой.

2,97

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&2&1\\
2&6&5\\
3&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
12\\
22\\
18\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		12

Найти наименьшие удельные затраты. Ответ округлить до целых.

605

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный объем поставки товара В. Ответ округлить до целых.

245

Даны данные за 10 дней о потребности в материальном ресурсе.

2,97

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

ящиков апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет math

день. Известно, что к началу первого дня остаток на складе составлял math

ящиков. Расход апельсинов в течение дня и поставки на склад характеризуются случайными нормально распределенными величинами. Проанализируйте план поставок апельсинов на склад и выберите верный вариант ответа:

(1) план поставок оптимален, нехватка товара практически не наблюдается, увеличение промежутка между поставками на 30% приводит к дефициту товара на складе

(2) план поставок оптимален, увеличение промежутка между поставками на 30% не приводит к дефициту товара на складе

(3) план поставок неоптимален, регулярно наблюдается существенная нехватка товара на складе

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю II (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика A к получателю III (целое число).

Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-1
	1
	9
	2
	-8
	5

0,9

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				35
III				5
Наличие	25	5	20	50

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

320

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать общее количество груза экспедируемого в направлении A-I (целое число).

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	5	1	2	110
II	7	1	8	6	40
III	6	3	3	7	70
IV	4	2	1	3	50
Наличие	90	40	50	90	270

Найти оптимальный план перевозок и определить его стоимость.

(1) 1550

(2) 770

(3) 1680

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 30\\
3X_1+X_2+5X_3 \le 55\\
3X_1+2X_2+X_3 \le 9

Функция определена только при неотрицательных значениях переменных.

(1) 45

(2) 48

(3) 105

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	7	2	2	1	0	0	10
0	6	12	6	0	1	0	72
0	7	16	7	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	2,5	0	0	42	52,5	20

(3)

X1	X2	X3	X4	X5	X6	P
0	2	0	0	63	128	18

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего math

. Ответ округлить до двух знаков после запятой.

37,25

Состояние	1	2	3	4	5	6
0	5	3	4
1		2	2	7
2			4	6	2
3				3	5
4					3	7
5						9

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	5
	2
	-1
	3
	0,2

Найти физический объем спроса при цене обеспечивающей максимум товарооборота. Ответ введите с точностью до 1-й цифры после запятой.

2,5

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок неоптимален

(2) план поставок оптимален

(3) при увеличении объема поставок апельсинов на склад в три раза, в магазин будут поступать только свежие фрукты

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&5&4\\
8&2&3\\
4&5&7
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
52\\
70\\
91\end{matrix}

Найти значение главного определителя системы. Ответ — целое число.

-93

Известны следующие данные.

Стоимость заказа (руб.)		15
Потребность (шт./ед.времени)		35
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		14

Найти оптимальный размер заказа. Ответ округлить до целых.

229

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный объем поставки товара Г. Ответ округлить до целых.

548

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

0,94

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок неоптимален

(2) план поставок оптимален

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика B к потребителю III (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю I (целое число).

Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-1
	1
	9
	2
	-8
	5

0,9

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1320

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 1 (целое число).

230

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	8	6	4	6	70
II	2	7	2	3	30
III	5	7	8	3	40
IV	8	5	2	3	60
Наличие	80	10	50	60	200

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1260

(2) 1170

(3) 810

Найти при каких значениях фиктивных переменных, вводимых в симплекс методе, достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 30\\
3X_1+X_2+5X_3 \le 55\\
3X_1+2X_2+X_3 \le 9

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	7	3	2	1	0	0	15
0	6	12	6	0	1	0	72
0	7	16	7	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	105	40

(3)

X1	X2	X3	X4	X5	X6	P
0	3	0	0	54	112	27

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего произведения math

. Ответ округлить до двух знаков после запятой.

204,13

Состояние	1	2	3	4	5	6	7
0	5	3	4
1		2	2	7
2			4	6	2
3				3	5
4					3	7	2
5						9	3
6							4

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	5
	2
	-1
	3
	0,2

Найти максимально возможный товарооборот. Ответ введите с точностью до 3-й цифры после запятой.

3,125

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю III (целое число).

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
2&5&4\\
8&1&3\\
4&4&7
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
50\\
70\\
90\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

-118

Известны следующие данные.

Стоимость заказа (руб.)		15
Потребность (шт./ед.времени)		35
Стоимость хранения (руб./ед./ед.времени)		0,02
Цена товара (руб./ед.)		14

Найти наименьшие удельные затраты. Ответ округлить до целых.

495

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный период поставки товара А. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

5,06

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

день. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок неоптимален

(2) план поставок оптимален

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю II (целое число).

Найти цену, при которой спрос максимален, если спрос на товар зависит от цены math

как

. Ответ округлить до одного знака после запятой.

	-1
	1
	9

0,5

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				30
III				40
Наличие	25	40	25	90

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

625

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

190

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	8	6	4	6	70
II	2	7	2	3	30
III	5	7	8	3	40
IV	8	5	2	3	60
Наличие	80	10	50	60	200

Найти оптимальный план перевозок и определить его стоимость.

(1) 780

(2) 570

(3) 1180

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 30\\
3X_1+X_2+5X_3 \le 55\\
3X_1+2X_2+X_3 \le 9

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	5	2	1	0	20
0	3	1	0	1	35
1	-4	-6	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	25	60

(2)

X1	X2	X3	X4	P
0	20	1	16	60

(3)

X1	X2	X3	X4	P
0	5	10	0	20

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ округлить до двух знаков после запятой.

10,18

Состояние	1	2	3	4	5	6	7	8
0	5	3	4
1		2	2	7
2			4	6	2
3				3	5
4					3	7	2
5						9	3	2
6							4	4
7								6

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	7
	5
	-2
	2
	0,3

Найти равновесный спрос. Ответ округлите до 1-й цифры после запятой.

0,6

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

190

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&2&1\\
2&6&5\\
3&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
12\\
22\\
18\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		13
Потребность (шт./ед.времени)		42
Стоимость хранения (руб./ед./ед.времени)		0,015
Цена товара (руб./ед.)		11

Найти оптимальный размер заказа. Ответ округлить до целых.

270

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный период поставки товара Б. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

6,94

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

ящик апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) при уменьшении объема поставок апельсинов на склад в два раза, в магазине практически не будет наблюдаться дефицит апельсинов

(2) время между поставками на склад апельсинов можно увеличить на 40% без ущерба для покупателей

(3) на складе практически никогда не наблюдается дефицит фруктов при увеличении объемов поставок на склад на 25%

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика C к потребителю IV (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика B к получателю III (целое число).

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-1
	1
	9

9,25

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				65
III				50
Наличие	35	60	30	125

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1060

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 3 (целое число).

270

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	5	1	2	70
II	7	1	8	6	30
III	6	3	3	7	40
IV	4	2	1	3	60
Наличие	80	10	50	60	200

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1530

(2) 740

(3) 1940

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 20\\
3X_1+X_2+5X_3 \le 20\\
3X_1+2X_2+X_3 \le 30

Функция определена только при неотрицательных значениях переменных.

(1) 28

(2) 48

(3) 10

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	6	2	4	1	0	0	20
0	6	6	1	0	1	0	80
0	2	4	1	0	0	1	160
1	-4	-8	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	20	120	80

(2)

X1	X2	X3	X4	X5	X6	P
0	20	0	0	30	70	80

(3)

X1	X2	X3	X4	X5	X6	P
10	0	0	0	30	80	120

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ округлить до двух знаков после запятой.

2,65

Состояние	1	2	3	4	5	6	7	8	9
0	5	3	4
1		2	2	7
2			4	6	2
3				3	5
4					3	7	2
5						9	3	2
6							4	4	3
7								6	2
8									6

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	7
	5
	-2
	2
	0,3

Найти равновесную цену. Ответ округлите до 1-й цифры после запятой.

1,3

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	6	2	4	1	0	0	20
0	6	6	1	0	1	0	80
0	2	4	1	0	0	1	160
1	-4	-8	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	20	120	80

(2)

X1	X2	X3	X4	X5	X6	P
0	20	0	0	30	70	80

(3)

X1	X2	X3	X4	X5	X6	P
10	0	0	0	30	80	120

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1\;2\;1\\
2\;6\;5\\
3\;2\;8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
12\\
22\\
18\end{matrix}

Найти обратную матрицу и вычислить абсолютное значение ее определителя. Ответ округлить до четырех знаков после запятой.

0,0455

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Критический объем поставки		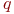12000
Цена товара если (руб./ед.)		12
Цена товара если (руб./ед.)		10

Найти оптимальный объем поставок. Ответ округлить до целых.

224

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальный период поставки товара В. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

4,12

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) площади склада используются нерационально

(2) время между поставками на склад апельсинов можно увеличить на 40% без ущерба для покупателей

(3) на складе практически никогда не наблюдается дефицит фруктов

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю IV (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе количество груза экспедируемого от поставщика C к получателю II (целое число).

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

7,13

Задана таблица транспортных тарифов.

	A	B	C
I	3	9	5
II	8	5	8
III	5	9	7

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				35
III				5
Наличие	25	5	20	50

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

385

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	7	5	8
II	4	3	8
III	5	4	6

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			15
II			30
Наличие	25	20
Продукт 3
	A	B	Потребность
I			30
II			20
Наличие	40	10

Решить многопродуктовую транспортную задачу. В ответе указать общие расходы на доставку всех трех продуктов (целое число).

690

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	5	1	2	70
II	7	1	8	6	30
III	6	3	3	7	40
IV	4	2	1	3	60
Наличие	80	10	50	60	200

Найти оптимальный план перевозок и определить его стоимость.

(1) 640

(2) 1570

(3) 2180

При следующих ограничениях:

X_1+2X_2+3X_3 \le 20\\
3X_1+X_2+5X_3 \le 30\\
3X_1+2X_2+X_3 \le 40

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	2	2	1	0	30
0	8	6	0	1	80
1	-2	-6	0	0	0

(1)

X1	X2	X3	X4	P
0	10/3	0	12	20

(2)

X1	X2	X3	X4	P
0	0	0	16	80

(3)

X1	X2	X3	X4	P
0	40/3	10/3	0	80

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение остаточного среднего квадратичного отклонения определяемого по формуле: math

. Ответ округлить до двух знаков после запятой.

1,74

Состояние	1	2	3	4	5	6	7	8	9	10
0	5	3	4
1		2	2	7
3				3	5
4					3	7	2
5						9	3	2
6							4	4	3
7								6	2
8									6	5
9										2

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	7
	5
	-2
	2
	0,3

Найти найти цену предложения, при которой товарооборот максимален. Ответ округлите до 1-й цифры после запятой.

0,7

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	12	3
2	24	5
3	35	6
4	46	7
5	51	7
6	63	8
7	78	8
8	82	9
9	94	9
10	102	10

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

. Ответ округлить до двух знаков после запятой.

1,74

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&5&4\\
8&2&3\\
4&5&7
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
52\\
70\\
91\end{matrix}

0,0108

Известны следующие данные.

Стоимость заказа (руб.)		10
Потребность (шт./ед.времени)		50
Стоимость хранения (руб./ед./ед.времени)		0,02
Критический объем поставки		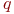12000
Цена товара если (руб./ед.)		12
Цена товара если (руб./ед.)		10

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		10	30	25	15
Потребность (шт./ед.времени)		50	80	120	100
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		12	7,5	9	10
Объем склада (ед.)	1500

Найти оптимальные удельные затраты при единичных объемах хранения каждого вида товаров. Ответ округлить до целых.

3330

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

7,88

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

ящика апельсинов в день. Среднее квадратичное отклонение периода поставки товара с базы на склад составляет math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) время между поставками на склад апельсинов можно увеличить на 15% без ущерба для покупателей

(2) время между поставками на склад апельсинов можно увеличить на 10% без ущерба для покупателей

(3) площади склада используются нерационально

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					90
II					45
III					130
IV					130
V					80
Наличие	50	175	100	150	475

Составить исходный план перевозок методом северо-западного угла. В ответе указать величину груза экспедируемого от поставщика D к потребителю V (целое число).

Задана таблица транспортных тарифов.

	A	B	C	D
I	7	3	5	2
II	4	1	6	4
III	5	8	3	5
IV	8	7	6	2
V	5	3	1	4

Задана таблица транспортных тарифов.

	A	B	C
I	7	1	5
II	2	5	2
III	5	1	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				20
II				75
III				60
Наличие	35	80	40	155

Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).

230

как

а стоимость хранения как math

	-4
	2
	5
	5
	-5
	4

Ответ округлить до одного знака после запятой.

1,5

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1020

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	9	5	7	100
II	1	3	5	2	40
III	4	7	3	5	60
IV	6	4	3	5	50
Наличие	80	40	40	90	250

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1250

(2) 1170

(3) 1060

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 6; 5.

Первый ресурс: 1 и 6.

Второй ресурс 3 и 1

Третий ресурс 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти программу производства, приносящую наибольшую прибыль.

(1) продукции первого вида 0 единиц второго вида 6 единиц

(2) продукции первого вида 2 единиц второго вида 0 единиц

(3) продукции первого вида 0 единиц второго вида 7 единиц

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	3	1	1	0	10
0	4	8	0	1	96
1	-4	-8	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	60

(2)

X1	X2	X3	X4	P
0	10	0	16	80

(3)

X1	X2	X3	X4	P
0	5	0	0	25

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение суммы весов. Ответ округлить до трех знаков после запятой.

0,235

Состояние	1	2	3
0	2	6	7
1		4	3
2			2

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	6
	3
	1
	2
	0,1

Найти равновесный спрос. Ответ округлите до целых.

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7,5

Найти оптимальный размер заказа. Ответ округлить до целых.

310

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6\;7\;9\\
2\;3\;5\\
7\;2\;8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
45\\
21\\
29\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7,5

Найти оптимальный размер заказа. Ответ округлить до целых.

310

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный объем поставки товара А. Ответ округлить до целых.

212

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку средней суточной потребности. Ответ округлить до одного знака после запятой.

6,4

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,005
	0,995
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти величину минимальных расходов на приобретение товаров, если цена товара зависит от объема партии math

как

, а стоимость хранения как math

	-4
	2
	5
	5
	-5
	4

Ответ округлить до двух знаков после запятой.

6,75

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

475

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	9	5	7	100
II	1	3	5	2	40
III	4	7	3	5	60
IV	6	4	3	5	50
Наличие	80	40	40	90	250

Найти оптимальный план перевозок и определить его стоимость.

(1) 970

(2) 1150

(3) 820

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 6; 5.

Первый ресурс: 1 и 6.

Второй ресурс 3 и 1

Третий ресурс 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти наибольшую прибыль.

(1) 12

(2) 10

(3) 30

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	4	1	1	0	10
0	6	5	0	1	96
1	-1	-7	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	90

(2)

X1	X2	X3	X4	P
0	10	0	46	70

(3)

X1	X2	X3	X4	P
0	5	0	20	35

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего math

. Ответ округлить до двух знаков после запятой.

7,16

Состояние	1	2	3	4
0	2	6	7
1		4	3	3
2			2	2
3				9

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	6
	3
	1
	2
	0,1

Найти равновесную цену. Ответ округлите до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

155

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6\;0\;4\\
2\;6\;5\\
10\;2\;8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
42\\
20\\
28\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

118

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7,5

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

155

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку дисперсии суточной потребности. Ответ округлить до двух знаков после запятой.

8,84

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,005
	0,995
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

995

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-4
	2
	5
	5
	-5
	4

0,9

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				40
II				120
III				10
Наличие	30	60	80	170

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

910

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	8	6	7	100
II	1	3	6	2	40
III	4	7	6	5	60
IV	6	4	3	5	50
Наличие	80	40	40	90	250

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1250

(2) 1170

(3) 1230

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 40\\
3X_1+X_2+5X_3 \le 15\\
3X_1+2X_2+X_3 \le 60

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	3	1	4	1	0	0	10
0	2	4	6	0	1	0	72
0	5	7	1	0	0	1	140
1	-3	-8	-2	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	12	80	90

(2)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	32	70	80

(3)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	36	80	90

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего квадрата math

. Ответ округлить до двух знаков после запятой.

58,82

Состояние	1	2	3	4	5
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					1

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	6
	3
	1
	2
	0,1

Найти найти цену предложения, при которой товарооборот максимален. Ответ округлите до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

2,97

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&2&5\\
2&6&4\\
2&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
10\\
20\\
12\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7,5

Найти наименьшие удельные затраты. Ответ округлить до целых.

616

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный объем поставки товара В. Ответ округлить до целых.

110

Даны данные за 10 дней о потребности в материальном ресурсе.

2,97

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

день. Известно, что к началу первого дня остаток на складе составлял math

(3) план поставок неоптимален, регулярно наблюдается существенная нехватка товара на складе

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-4
	2
	5
	5
	-5
	4

3,6

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				20
III				30
Наличие	15	30	15	90

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

345

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	8	6	7	100
II	1	3	6	2	40
III	4	7	6	5	60
IV	6	4	3	5	50
Наличие	80	40	40	90	250

Найти оптимальный план перевозок и определить его стоимость.

(1) 1010

(2) 1550

(3) 1680

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 40\\
3X_1+X_2+5X_3 \le 15\\
3X_1+2X_2+X_3 \le 60

Функция определена только при неотрицательных значениях переменных.

(1) 105

(2) 48

(3) 45

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	3	4	4	1	0	0	10
0	2	12	6	0	1	0	72
0	5	35	1	0	0	1	140
1	-3	-8	-2	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	2,5	0	0	42	52,5	20

(3)

X1	X2	X3	X4	X5	X6	P
0	2	0	0	63	128	18

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего math

. Ответ округлить до одного знака после запятой.

43,2

Состояние	1	2	3	4	5	6
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					3	3
5						8

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	6
	3
	1
	2
	0,1

Найти физический объем спроса при цене обеспечивающей максимум товарооборота. Ответ округлите до целых.

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок оптимален

(2) в магазине наблюдается постоянный острый дефицит апельсинов

(3) в магазине не будет наблюдаться дефицит апельсинов, если период поставок фруктов на склад уменьшить в два раза

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6&7&9\\
2&3&5\\
7&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
45\\
21\\
29\end{matrix}

Найти значение главного определителя системы. Ответ — целое число.

Известны следующие данные.

Стоимость заказа (руб.)		32
Потребность (шт./ед.времени)		81
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7

Найти оптимальный размер заказа. Ответ округлить до целых.

322

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный объем поставки товара Г. Ответ округлить до целых.

548

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

0,94

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок оптимален

(2) в магазине наблюдается постоянный острый дефицит апельсинов

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

3,6

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1760

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 1 (целое число).

260

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	9	5	7	20
II	1	3	5	2	40
III	4	7	3	5	30
IV	6	4	3	5	20
Наличие	40	20	10	40	110

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 390

(2) 1260

(3) 810

При следующих ограничениях:

X_1+2X_2+3X_3 \le 40\\
3X_1+X_2+5X_3 \le 15\\
3X_1+2X_2+X_3 \le 60

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	3	5	4	1	0	0	25
0	2	12	6	0	1	0	72
0	5	35	1	0	0	1	280
1	-3	-8	-2	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	105	40

(3)

X1	X2	X3	X4	X5	X6	P
0	3	0	0	54	112	27

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего произведения math

. Ответ округлить до двух знаков после запятой.

234,61

Состояние	1	2	3	4	5	6	7
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					3	3	4
5						8	7
6							1

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	6
	3
	1
	2
	0,1

Найти максимально возможный товарооборот. Ответ округлите до целых.

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6&0&4\\
2&6&5\\
10&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
42\\
20\\
28\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		32
Потребность (шт./ед.времени)		81
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		7

Найти наименьшие удельные затраты. Ответ округлить до целых.

583

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный период поставки товара А. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

5,46

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) уровни расхода и поставок фруктов на склад выровняются к исходу первого месяца работы склада

(2) в магазине наблюдается острый дефицит апельсинов

(3) в магазине будет наблюдаться дефицит апельсинов, если период поставок фруктов на склад уменьшить в два раза

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти цену, при которой спрос максимален, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-4
	2
	5

0,25

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

805

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

185

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	9	5	7	20
II	1	3	5	2	40
III	4	7	3	5	30
IV	6	4	3	5	20
Наличие	40	20	10	40	110

Найти оптимальный план перевозок и определить его стоимость.

(1) 1180

(2) 880

(3) 350

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 40\\
3X_1+X_2+5X_3 \le 25\\
3X_1+2X_2+X_3 \le 50

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	7	1	1	0	10
0	4	2	0	1	40
1	-2	-8	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	10	60

(2)

X1	X2	X3	X4	P
0	15	0	16	60

(3)

X1	X2	X3	X4	P
0	10	0	20	80

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ записать с точностью до двух знаков после запятой.

-9,87

Состояние	1	2	3	4	5	6	7	8
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					3	3	4
5						8	7	7
6							1	5
7								3

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	8
	3
	1
	5
	0,1

Найти равновесный спрос. Ответ округлите до 1-й цифры после запятой.

5,4

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

185

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1&2&5\\
2&6&4\\
2&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
10\\
20\\
12\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

-16

Известны следующие данные.

Стоимость заказа (руб.)		31
Потребность (шт./ед.времени)		41
Стоимость хранения (руб./ед./ед.времени)		0,05
Цена товара (руб./ед.)		6,5

Найти оптимальный размер заказа. Ответ округлить до целых.

226

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный период поставки товара Б. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

7,34

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) уровни расхода и поставок фруктов на склад выровняются к исходу первого месяца работы склада

(2) в магазине наблюдается острый дефицит апельсинов в первую неделю работы

(3) в первую неделю в магазине не будет наблюдаться дефицит апельсинов, если период поставок фруктов на склад уменьшить в два раза

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-4
	2
	5

5,25

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				40
II				120
III				10
Наличие	30	60	80	170

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1460

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 3 (целое число).

465

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	8	6	7	20
II	1	3	6	2	40
III	4	7	6	5	30
IV	6	4	3	5	20
Наличие	40	20	10	40	110

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 420

(2) 1440

(3) 940

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 30\\
3X_1+X_2+5X_3 \le 10\\
3X_1+2X_2+X_3 \le 60

Функция определена только при неотрицательных значениях переменных.

(1) 70

(2) 48

(3) 45

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	2	2	4	1	0	0	20
0	6	1	1	0	1	0	60
0	2	4	1	0	0	1	140
1	-6	-8	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
10	0	0	0	0	120	60

(2)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	0	20	60

(3)

X1	X2	X3	X4	X5	X6	P
10	10	0	0	20	80	60

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ округлить до двух знаков после запятой.

113,87

Состояние	1	2	3	4	5	6	7	8	9
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					3	3	4
5						8	7	7
6							1	5	9
7								3	5
8									3

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	8
	3
	1
	5
	0,1

Найти равновесную цену. Ответ округлите до 1-й цифры после запятой.

0,9

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	2	2	4	1	0	0	20
0	6	1	1	0	1	0	60
0	2	4	1	0	0	1	140
1	-6	-8	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
10	0	0	0	0	120	60

(2)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	0	20	60

(3)

X1	X2	X3	X4	X5	X6	P
10	10	0	0	20	80	60

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
1\;2\;5\\
2\;6\;4\\
2\;2\;8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
10\\
20\\
12\end{matrix}

0,0625

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Критический объем поставки		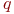14000
Цена товара если (руб./ед.)		7,5
Цена товара если (руб./ед.)		6

Найти оптимальный объем поставок. Ответ округлить до целых.

310

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

Найти оптимальный период поставки товара В. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

4,52

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) уровни расхода и поставок фруктов на склад выровняются к исходу первого месяца работы склада

(2) в магазине наблюдается острый дефицит апельсинов

(3) в первую неделю в магазине не будет наблюдаться дефицит апельсинов

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ ввести в виде целого числа.

	-1
	2
	5

Задана таблица транспортных тарифов.

	A	B	C
I	2	9	1
II	8	5	9
III	9	9	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				10
II				20
III				30
Наличие	15	30	15	60

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

535

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	9	7	10
II	6	5	10
III	7	6	8

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			15
II			30
Наличие	5	40
Продукт 2
	A	B	Потребность
I			10
II			20
Наличие	15	15
Продукт 3
	A	B	Потребность
I			35
II			30
Наличие	50	15

910

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	4	8	6	7	20
II	1	3	6	2	40
III	4	7	6	5	30
IV	6	4	3	5	20
Наличие	40	20	10	40	110

Найти оптимальный план перевозок и определить его стоимость.

(1) 370

(2) 1020

(3) 280

При следующих ограничениях:

X_1+2X_2+3X_3 \le 50\\
3X_1+X_2+5X_3 \le 10\\
3X_1+2X_2+X_3 \le 40

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	6	4	1	0	10
0	4	8	0	1	40
1	-4	-8	0	0	0

(1)

X1	X2	X3	X4	P
0	5	0	10	20

(2)

X1	X2	X3	X4	P
0	2.5	0	20	20

(3)

X1	X2	X3	X4	P
2.5	5.5	0	0	25

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

. Ответ округлить до трех знаков после запятой.

1,485

Состояние	1	2	3	4	5	6	7	8	9	10
0	2	6	7
1		4	3	3
2			2	2	1
3				9	9
4					3	3	4
5						8	7	7
6							1	5	9
7								3	5
8									3	9
9										3

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	8
	3
	1
	5
	0,1

1,3

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	102	10
2	95	10
3	83	9
4	77	8
5	65	8
6	52	7
7	46	7
8	37	6
9	24	5
10	15	4

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

. Ответ округлить до трех знаков после запятой.

1,485

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6&7&9\\
2&3&5\\
7&2&8
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
45\\
21\\
29\end{matrix}

0,0156

Известны следующие данные.

Стоимость заказа (руб.)		30
Потребность (шт./ед.времени)		80
Стоимость хранения (руб./ед./ед.времени)		0,05
Критический объем поставки		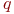14000
Цена товара если (руб./ед.)		7,5
Цена товара если (руб./ед.)		6

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		15	10	15	10
Потребность (шт./ед.времени)		30	60	40	150
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		10	8	7	13
Объем склада (ед.)	1300

3038

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

8,28

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) уровни расхода и поставок фруктов на склад выровняются к исходу первого месяца работы склада

(2) в магазине наблюдается острый дефицит апельсинов

(3) в первую неделю в магазине будет часто наблюдаться дефицит апельсинов

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					80
II					55
III					110
IV					115
V					50
Наличие	60	155	55	140	410

Задана таблица транспортных тарифов.

	A	B	C	D
I	5	8	6	1
II	2	5	3	1
III	3	4	4	2
IV	6	1	5	5
V	2	2	2	3

Задана таблица транспортных тарифов.

	A	B	C
I	8	1	9
II	2	5	1
III	1	1	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				50
II				130
III				20
Наличие	40	70	90	200

Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).

240

как

а стоимость хранения как math

	-3
	4
	7
	4
	-7
	5

Ответ округлить до одного знака после запятой.

1,5

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1170

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	3	7	4	6	100
II	2	4	3	3	40
III	3	5	6	3	60
IV	5	5	2	6	50
Наличие	80	40	40	90	250

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 1060

(2) 1250

(3) 1530

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 5; 4.

Первый ресурс: 1 и 6.

Второй ресурс 3 и 1

Третий ресурс 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти программу производства, приносящую наибольшую прибыль.

(1) продукции первого вида 2 единиц второго вида 0 единиц

(2) продукции первого вида 0 единиц второго вида 6 единиц

(3) продукции первого вида 0 единиц второго вида 7 единиц

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	4	1	1	0	5
0	2	9	0	1	45
1	-4	-5	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	60

(2)

X1	X2	X3	X4	P
0	10	0	16	80

(3)

X1	X2	X3	X4	P
0	5	0	0	25

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение суммы весов. Ответ округлить до двух знаков после запятой.

0,49

Состояние	1	2	3
0	4	5	7
1			5
2			7

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	4
	2
	2
	2
	0,4

Найти равновесный спрос. Ответ округлите до целых.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Цена товара (руб./ед.)		9

Найти оптимальный размер заказа. Ответ округлить до целых.

245

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
3\;2\;4\\
5\;7\;8\\
2\;4\;1
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
44\\
97\\
36\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Цена товара (руб./ед.)		9

Найти оптимальный размер заказа. Ответ округлить до целых.

245

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный объем поставки товара А. Ответ округлить до целых.

150

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку средней суточной потребности. Ответ округлить до одного знака после запятой.

7,9

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,01
	0,99
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти величину минимальных расходов на приобретение товаров, если цена товара зависит от объема партии math

как

, а стоимость хранения как math

	-3
	4
	7
	4
	-7
	5

Ответ округлить до двух знаков после запятой.

9,75

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				100
III				25
Наличие	60	60	40	160

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

855

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	3	7	4	6	100
II	2	4	3	3	40
III	3	5	6	3	60
IV	5	5	2	6	50
Наличие	80	40	40	90	250

Найти оптимальный план перевозок и определить его стоимость.

(1) 1020

(2) 930

(3) 820

Производство двух видов продукции приносит прибыль в расчете на единицу, соответственно, 5; 4.

Первый ресурс: 1 и 6.

Второй ресурс 3 и 1

Третий ресурс 4 и 7.

Ресурсы имеются в количествах, соответственно: 54; 6 и 42.

Найти наибольшую прибыль.

(1) 24

(2) 12

(3) 42

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	3	1	1	0	5
0	6	5	0	1	45
1	-3	-7	0	0	0

(1)

X1	X2	X3	X4	P
0	10	0	12	90

(2)

X1	X2	X3	X4	P
0	10	0	46	70

(3)

X1	X2	X3	X4	P
0	5	0	20	35

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего math

. Ответ округлить до двух знаков после запятой.

2,84

Состояние	1	2	3	4
0	4	5	7
1			5	5
2			7	3
3				6

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	4
	2
	2
	2
	0,4

Найти равновесную цену. Ответ введите с точностью до 1-й цифры после запятой.

0,5

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

190

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6\;2\;4\\
8\;2\;8\\
2\;4\;6
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
40\\
20\\
36\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Цена товара (руб./ед.)		9

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный объем поставки товара Б. Ответ округлить до целых.

190

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти оценку дисперсии суточной потребности. Ответ округлить до двух знаков после запятой.

14,09

Пусть вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. Аналогично, вероятность того, что в течение дня потребуется math

- ремонтных комплектов составляет math

. При этом, величины math

являются случайными с математическими ожиданиями: math

и средними квадратичными отклонениями: math

Исследуйте распределение случайных величин определяющих расход ремонтных комплектов за math

дней.

	0,01
	0,99
	1000
	20
	10
	2
	1

Укажите ожидаемое количество дней (целое число), в течение которых расход составит math

комплектов.

990

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти цену, при которой спрос равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до двух знаков после запятой.

	-3
	4
	7
	4
	-7
	5

1,74

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				25
II				125
III				15
Наличие	50	50	65	165

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1060

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	2	3	4	5	100
II	1	2	4	6	40
III	3	1	5	1	60
IV	4	1	2	4	50
Наличие	80	40	40	90	250

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 680

(2) 1250

(3) 1170

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 6\\
3X_1+X_2+5X3_ \le 21\\
3X_1+2X_2+X_3 \le 300

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	4	1	3	1	0	0	10
0	6	4,5	2	0	1	0	81
0	1	8	5	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	12	80	90

(2)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	32	70	80

(3)

X1	X2	X3	X4	X5	X6	P
0	10	0	0	36	80	90

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего квадрата math

. Ответ округлить до двух знаков после запятой.

14,69

Состояние	1	2	3	4	5
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	4
	2
	2
	2
	0,4

Найти найти цену предложения, при которой товарооборот максимален. Ответ округлите до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

3,75

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
4&6&6\\
8&2&4\\
6&2&4
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
6\\
2\\
8\end{matrix}

Найти сумму корней системы. Ответ -- целое число.

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Цена товара (руб./ед.)		9

Найти наименьшие удельные затраты. Ответ округлить до целых.

1105

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный объем поставки товара В. Ответ округлить до целых.

200

Даны данные за 10 дней о потребности в материальном ресурсе.

3,75

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(2) план поставок неоптимален, регулярно наблюдается существенная нехватка товара на складе

(3) план поставок оптимален, увеличение промежутка между поставками на 30% не приводит к дефициту товара на складе

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти величину спроса, при котором он равен предложению, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-3
	4
	7
	4
	-7
	5

4,9

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				25
II				90
III				15
Наличие	50	50	30	130

Найти минимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

745

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	2	3	4	5	100
II	1	2	4	6	40
III	3	1	5	1	60
IV	4	1	2	4	50
Наличие	80	40	40	90	250

Найти оптимальный план перевозок и определить его стоимость.

(1) 510

(2) 1570

(3) 1550

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 6\\
3X_1+X_2+5X_3 \le 21\\
3X_1+2X_2+X_3 \le 30

Функция определена только при неотрицательных значениях переменных.

(1) 45

(2) 48

(3) 105

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	4	5	3	1	0	0	10
0	6	9	2	0	1	0	81
0	1	16	5	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	2,5	0	0	42	52,5	20

(3)

X1	X2	X3	X4	X5	X6	P
0	2	0	0	63	128	18

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего math

. Ответ округлить до трех знаков после запятой.

21,275

Состояние	1	2	3	4	5	6
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2	5
5						7

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	4
	2
	2
	2
	0,4

Найти физический объем спроса при цене обеспечивающей максимум товарооборота. Ответ округлите до целых.

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок оптимален в первые две недели, нехватка товара практически не наблюдается, увеличение промежутка между поставками на 30% приводит к дефициту товара на складе

(2) план поставок может считаться оптимальным только в первую неделю

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
3&2&4\\
5&7&8\\
2&4&1
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
44\\
97\\
36\end{matrix}

Найти значение главного определителя системы. Ответ — целое число.

-29

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		100
Стоимость хранения (руб./ед./ед.времени)		0,15
Цена товара (руб./ед.)		9,4

Найти оптимальный размер заказа. Ответ округлить до целых.

183

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный объем поставки товара Г. Ответ округлить до целых.

445

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти погрешность оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

1,19

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(2) план поставок может считаться оптимальным только в первую неделю

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти величину предложения, при котором оно равно спросу, если спрос на товар зависит от цены math

как

, а предложение как math

. Ответ округлить до одного знака после запятой.

	-3
	4
	7
	4
	-7
	5

4,9

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1695

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 1 (целое число).

170

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	3	7	4	6	60
II	2	4	3	3	30
III	3	5	6	3	30
IV	5	5	2	6	30
Наличие	10	70	50	20	150

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 800

(2) 1260

(3) 810

При следующих ограничениях:

X_1+2X_2+3X_3 \le 6\\
3X_1+X_2+5X_3 \le 21\\
3X_1+2X_2+X_3 \le 30

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	4	9	3	1	0	0	27
0	6	9	2	0	1	0	81
0	1	16	5	0	0	1	160
1	-4	-9	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	80	45

(2)

X1	X2	X3	X4	X5	X6	P
0	5	0	0	12	105	40

(3)

X1	X2	X3	X4	X5	X6	P
0	3	0	0	54	112	27

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение среднего произведения math

. Ответ округлить до двух знаков после запятой.

116,66

Состояние	1	2	3	4	5	6	7
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2	5	8
5						7	2
6							5

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	4
	2
	2
	2
	0,4

Найти максимально возможный товарооборот. Ответ округлите до целых.

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	5	7	2	6
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
6&2&4\\
8&2&8\\
2&4&6
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
40\\
20\\
36\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

-72

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		100
Стоимость хранения (руб./ед./ед.времени)		0,15
Цена товара (руб./ед.)		9,4

Найти наименьшие удельные затраты. Ответ округлить до целых.

967

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный период поставки товара А. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

6,71

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

день. Известно, что к началу первого дня остаток на складе составлял math

(2) в магазине не будет наблюдаться дефицит апельсинов

(3) план поставок оптимален, увеличение промежутка между поставками на 30% приводит к дефициту товара на складе

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти цену, при которой спрос максимален, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-3
	4
	7

0,67

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				100
III				25
Наличие	60	60	40	160

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1380

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

220

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	3	7	4	6	60
II	2	4	3	3	30
III	3	5	6	3	30
IV	5	5	2	6	30
Наличие	10	70	50	20	150

Найти оптимальный план перевозок и определить его стоимость.

(1) 610

(2) 880

(3) 1180

Найти при каких значениях переменных достигает максимума целевая функция:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 10\\
3X_1+X_2+5X3_ \le 20\\
3X_1+2X_2+X_3 \le 30

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	8	5	1	0	20
0	2	3	0	1	50
1	-4	-6	0	0	0

(1)

X1	X2	X3	X4	P
0	15	0	10	40

(2)

X1	X2	X3	X4	P
0	4	0	38	24

(3)

X1	X2	X3	X4	P
0	5	10	0	20

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ округлить до одного знака после запятой.

8,5

Состояние	1	2	3	4	5	6	7	8
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2	5	8
5						7	2	3
6							5	7
7								9

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	3
	2,5
	1
	2
	0,3

Найти равновесный спрос. Ответ округлите до 1-й цифры после запятой.

1,9

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 2 (целое число).

220

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
4&6&6\\
8&2&4\\
6&2&4
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
6\\
2\\
8\end{matrix}

Найти значение главного определителя системы. Ответ -- целое число.

-24

Известны следующие данные.

Стоимость заказа (руб.)		20
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,01
Цена товара (руб./ед.)		10

Найти оптимальный размер заказа. Ответ округлить до целых.

693

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный период поставки товара Б. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

9,09

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок оптимален только в первые две недели, нехватка товара практически не наблюдается, увеличение промежутка между поставками на 30% приводит к дефициту товара на складе

(2) в первый месяц работы на складе практически не наблюдается нехватки товара

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-3
	4
	7

8,33

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				25
II				125
III				15
Наличие	50	50	65	165

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1415

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

Решить многопродуктовую транспортную задачу. В ответе указать расходы на доставку продукта 3 (целое число).

285

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	2	3	4	5	60
II	1	2	4	6	30
III	3	1	5	1	30
IV	4	1	2	4	30
Наличие	10	70	50	20	150

Создать исходный план перевозок методом северо-западного угла и определить его стоимость.

(1) 500

(2) 440

(3) 1250

Найти значение максимума целевой функции:

При следующих ограничениях:

X_1+2X_2+3X_3 \le 10\\
3X_1+X_2+5X_3 \le 10\\
3X_1+2X_2+X_3 \le 60

Функция определена только при неотрицательных значениях переменных.

(1) 45

(2) 32

(3) 105

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	2	2	4	1	0	0	30
0	8	1	1	0	1	0	45
0	1	4	1	0	0	1	120
1	-8	-4	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
30/7	75/7	0	0	0	510/7	540/7

(2)

X1	X2	X3	X4	X5	X6	P
0	10/7	0	0	36/7	70	80

(3)

X1	X2	X3	X4	X5	X6	P
30	75	0	0	36	160	90/7

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

статистические веса. В ответе указать значение math

. Ответ записать с точностью до двух знаков после запятой.

-2,86

Состояние	1	2	3	4	5	6	7	8	9
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2	5	8
5						7	2	3
6							5	7	4
7								9	3
8									7

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	3
	2,5
	1
	2
	0,3

Найти равновесную цену. Ответ округлите до 1-й цифры после запятой.

0,4

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4	X5	X6
0	2	2	4	1	0	0	30
0	8	1	1	0	1	0	45
0	1	4	1	0	0	1	120
1	-8	-4	-4	0	0	0	0

(1)

X1	X2	X3	X4	X5	X6	P
30/7	75/7	0	0	0	510/7	540/7

(2)

X1	X2	X3	X4	X5	X6	P
0	10/7	0	0	36/7	70	80

(3)

X1	X2	X3	X4	X5	X6	P
30	75	0	0	36	160	90/7

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
4\;6\;6\\
8\;2\;4\\
6\;2\;4
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
6\\
2\\
8\end{matrix}

0,0417

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Критический объем поставки		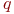10000
Цена товара если (руб./ед.)		9
Цена товара если (руб./ед.)		7

Найти оптимальный объем поставок. Ответ округлить до целых.

245

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

Найти оптимальный период поставки товара В. Ответ округлить до целых.

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти нижнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

5,53

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок оптимален только в первые две недели

(2) к исходу первой недели работы потребители практически не могут купить апельсины

(3) план поставок оптимален

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Найти максимальный уровень спроса, если спрос на товар зависит от цены math

как

. Ответ округлить до двух знаков после запятой.

	-1
	3
	7

9,25

Задана таблица транспортных тарифов.

	A	B	C
I	1	8	6
II	9	6	9
III	6	8	4

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				25
II				90
III				15
Наличие	50	50	30	130

Найти максимальный по стоимости план перевозок и определить его стоимость. Ответ -- целое число.

1100

Имеются три поставщика math

и три потребителя math

. Задана матрица транспортных тарифов.

	A	B	C
I	6	4	7
II	3	2	7
III	4	3	5

Есть данные о наличии и потребности в трех видах продукции.

	A	B	Потребность
Продукт 1
I			20
II			40
Наличие	10	50
Продукт 2
	A	B	Потребность
I			20
II			50
Наличие	40	30
Продукт 3
	A	B	Потребность
I			35
II			35
Наличие	55	15

675

Задана транспортная таблица.

Потребители	Поставщики				Потребность
Потребители	I	II	III	IV	Потребность
I	2	3	4	5	60
II	1	2	4	6	30
III	3	1	5	1	30
IV	4	1	2	4	30
Наличие	10	70	50	20	150

Найти оптимальный план перевозок и определить его стоимость.

(1) 1800

(2) 340

(3) 1570

При следующих ограничениях:

X_1+2X_2+3X_3 \le 10\\
3X_1+X_2+5X_3 \le 10\\
3X_1+2X_2+X_3 \le 40

Функция определена только при неотрицательных значениях переменных.

(1)

(2)

(3)

Дана симплекс таблица. Найти решение.

P	X1	X2	X3	X4
0	8	2	1	0	25
0	4	8	0	1	65
1	-6	-8	0	0	0

(1)

X1	X2	X3	X4	P
1.25	7.5	0	0	67.5

(2)

X1	X2	X3	X4	P
2.25	10	0	16.5	80

(3)

X1	X2	X3	X4	P
1	5	2	0	25

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

. Ответ округлить до двух знаков после запятой.

2,79

Состояние	1	2	3	4	5	6	7	8	9	10
0	4	5	7
1			5	5
2			7	3	6
3				6	4
4				1	2	5	8
5						7	2	3
6							5	7	4
7								9	3
8									7	4
9										6

Пусть спрос подчиняется закону math

, где

-цена. Предложение зависит от цены math

следующим образом: math

. При изменении баланса спроса и предложения цена изменяется в соответствии с законом: math

. Решение этого дифференциально уравнения имеет вид: math

; где

- цена до изменения баланса спроса и предложения.

	3
	2,5
	1
	2
	0,3

0,6

Заданы

наборов (

) значений двух переменных: math

(уровень сервисного обслуживания) и math

(уровень целевого параметра - экономический эффект). Величина math

- это оценочное значение, полученное с погрешностью math


1	4	2
2	17	4
3	25	5
4	37	6
5	43	6
6	51	7
7	57	7
8	62	8
9	70	8
10	75	9

Построить уравнение линейной регрессии: math

, где

. Для вычисления средних значений используются формулы:

\bar x=\frac{\sum_{i=1}^n (x_iw_i)}{\sum_{i=1}^n w_i},\\
\bar y=\frac{\sum_[i=1}^n(y_iw_i)}{\sum_{i=1}^n w_i};\\
\overline {xy}=\frac{\sum_{i=1}^n(x_iy_iw_i)}{\sum_{i=1}^nw_i};\\
\overline {x^2}=\frac{\sum_{i=1}^n(x_i^2w_i)}{\sum_{i=1}^nw_i}.

Здесь

. Ответ округлить до двух знаков после запятой.

2,79

Дана матрица левой части системы линейных алгебраических уравнений:

\begin{matrix}
3&2&4\\
5&7&8\\
2&4&1
\end{matrix}

Дан столбец свободных членов:

\begin{matrix}
44\\
97\\
36\end{matrix}

0,0345

Известны следующие данные.

Стоимость заказа (руб.)		25
Потребность (шт./ед.времени)		120
Стоимость хранения (руб./ед./ед.времени)		0,1
Критический объем поставки		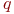10000
Цена товара если (руб./ед.)		9
Цена товара если (руб./ед.)		7

Найти оптимальный период поставок. Ответ округлить до целых.

Известны следующие данные.

Виды товаров		A	Б	В	Г
Стоимость заказа (руб.)		5	12	16	11
Потребность (шт./ед.времени)		45	75	125	90
Стоимость хранения (руб./ед./ед.времени)		0,02	0,05	0,1	0,01
Цена товара (руб./ед.)		7	5	3	12
Объем склада (ед.)	1000

2182

Даны данные за 10 дней о потребности в материальном ресурсе.

Найти верхнюю границу доверительного интервала math

для оценки средней суточной потребности. Ответ округлить до двух знаков после запятой.

10,27

С базы на склад в среднем раз в math

дней поставляют апельсины в количестве math

ящиков. Объем поставок со склада в ближайший магазин случаен и характеризуется средним количеством в math

ящиков апельсинов в день, со средним квадратичным отклонением math

дня. Известно, что к началу первого дня остаток на складе составлял math

(1) план поставок существенно неоптимален

(2) дефицит апельсинов в магазине можно ликвидировать, если уменьшить период между поставками фруктов на склад в два раза

(3) план поставок оптимален

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	D	Потребность
I					40
II					35
III					70
IV					35
V					60
Наличие	20	95	50	75	240

Задана таблица транспортных тарифов.

	A	B	C	D
I	9	2	3	3
II	3	3	4	5
III	5	7	2	6
IV	7	5	1	3
V	2	4	4	3

Задана таблица транспортных тарифов.

	A	B	C
I	9	2	4
II	1	4	1
III	4	2	6

Заданы сведения о наличии груза у отправителей и потребность в грузе у получателей.

	A	B	C	Потребность
I				35
II				135
III				25
Наличие	60	60	75	195

Решить транспортную задачу. В ответе указать минимальные расходы на перевозку (целое число).

255