Главная /
Базы данных /
Статистические методы анализа данных
Статистические методы анализа данных - ответы на тесты Интуит
Правильные ответы выделены зелёным цветом.
Все ответы: Курс посвящен изучению современных методов анализа данных.
Все ответы: Курс посвящен изучению современных методов анализа данных.
Смотрите также:
Известны парные коэффициенты корреляции случайных величин ![math]()
: ![math]()
Частный коэффициент корреляции случайных величин ![math]()
и ![math]()
при фиксированном значении ![math]()
будет
: 
Частный коэффициент корреляции случайных величин 
и 
при фиксированном значении 
будет
(1) положительным
(2) отрицательным
(3) равным нулю
Фактором в задаче однофакторного дисперсионного анализа называют
(1) значение измеряемого признака
(2) переменную, которая влияет на значение измеряемого признака
(3) погрешность измеряемого признака
Переменная ![math]()
измерена в количественной шкале. Результаты измерений этой переменной
измерена в количественной шкале. Результаты измерений этой переменной
(1) можно представить в порядковой шкале измерений
(2) можно представить в номинальной шкале измерений
(3) нельзя представить в какой-либо другой шкале измерений
Признаки ![math]()
и ![math]()
измерены в номинальной шкале. Какой критерий можно применить для проверки гипотезы о независимости этих признаков?
и измерены в номинальной шкале. Какой критерий можно применить для проверки гипотезы о независимости этих признаков?
(1) ранговый критерий Спирмена
(2) ранговый критерий Кендэла
(3) критерий хи-квадрат Фишера-Пирсона
(4) критерий, основанный на выборочном коэффициенте корреляции
Каким (какими) из перечисленных свойств удовлетворяет корреляционное отношение ![math]()
переменной ![math]()
по ![math]()
?
переменной по ?
(1) ![math]()
(2) ![math]()
(3) если переменные ![math]()
и ![math]()
связаны соотношением ![math]()
, то ![math]()
и связаны соотношением 
, то 
Задача однофакторного дисперсионного анализа является обобщением задачи проверки гипотезы об однородности двух выборок против альтернативы о том, что рассматриваемые выборки различаются
(1) параметром масштаба
(2) параметром сдвига
(3) типом распределения
Переменная ![math]()
измеряется в номинальной шкале и имеет 5 градаций, переменная ![math]()
измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные ![math]()
и ![math]()
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
измеряется в номинальной шкале и имеет 5 градаций, переменная 
измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные и зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
(1) 10
(2) 4
(3) 9
(4) 7
Сто (100) студентов прошли тестирование по математическому анализу и по физике. Пусть переменная Х- рейтинг студентов по математическому анализу, а переменная Y- рейтинг по физике. Коэффициент корреляции Спирмена для переменных ![math]()
и ![math]()
оказался равным 0.6. Эта информация
и оказался равным 0.6. Эта информация
(1) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная положительная связь
и существует монотонная положительная связь
(2) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная отрицательная связь
и существует монотонная отрицательная связь
(3) позволяет сделать вывод о том, что на уровне значимости 0.05 нет оснований для отклонения гипотезы о независимости показателей ![math]()
и ![math]()
и
(4) не позволяет сделать вывод о зависимости или независимости показателей ![math]()
и ![math]()
и МНК-оценка параметра ![math]()
линейной регрессионной модели является
линейной регрессионной модели является
(1) смещенной оценкой параметра ![math]()
(2) несмещенной оценкой параметра ![math]()
только при гауссовском распределении шумов
только при гауссовском распределении шумов
(3) несмещенной оценкой параметра ![math]()
при любом распределении шумов
при любом распределении шумов Погрешности наблюдений в модели однофакторного дисперсионного анализа должны удовлетворять следующим условиям:
(1) быть независимыми и иметь стандартное гауссовское распределение
(2) быть независимыми и иметь гауссовское распределение с известными параметрами m и ![math]()
(3) быть независимыми и иметь гауссовское распределение с неизвестными параметрами m и ![math]()
(4) быть независимыми и иметь одинаковые распределения с нулевым математическим ожиданием
Для номинального признака ![math]()
, имеющего 5 градаций, и номинального признака ![math]()
, имеющего 4 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 23.13. Согласно таблицам, квантили распределения хи-квадрат ![math]()
, ![math]()
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
, имеющего 5 градаций, и номинального признака , имеющего 4 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 23.13. Согласно таблицам, квантили распределения хи-квадрат 
, 
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
(1) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть
(2) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует принять
и следует принять
(3) на уровне значимости 0.01 нет оснований для отклонения гипотезы о независимости признаков ![math]()
и ![math]()
и
(4) на уровне значимости 0.01 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть В ходе эксперимента получена реализация двумерной выборки. Известно, что первое наблюдение (5;3) , а второе (3;1). Можно сказать, что эти пары
(1) согласованы
(2) несогласованы
(3) коррелированны
(4) некоррелированны
Рассматривается модель линейной регрессии ![math]()
, ![math]()
, где ![math]()
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения ![math]()
. Для оценивания неизвестных параметров ![math]()
применен метод наименьших квадратов (МНК). Величины дисперсий ![math]()
, полученных МНК-оценок, зависят от
, 
, где 
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения 
. Для оценивания неизвестных параметров 
применен метод наименьших квадратов (МНК). Величины дисперсий 
, полученных МНК-оценок, зависят от
(1) вида матрицы плана
(2) значения ![math]()
(3) дисперсии погрешностей ![math]()
(4) константы ![math]()
Наблюдения ![math]()
описываются моделью следующего вида ![math]()
, где
![math]()
-неизвестное общее среднее, ![math]()
-отклонение от среднего, вызванное изменением уровня факторной переменной, ![math]()
- погрешности с нулевым математическим ожиданием.
Контраст ![math]()
параметров ![math]()
в этой модели задан следующим образом
![math]()
, где ![math]()
.
Определенный таким образом контраст характеризует
описываются моделью следующего вида 
, где
-неизвестное общее среднее, 
-отклонение от среднего, вызванное изменением уровня факторной переменной, 
- погрешности с нулевым математическим ожиданием.
Контраст параметров 
в этой модели задан следующим образом
, где 
.
Определенный таким образом контраст характеризует
(1) среднее значение отклика
(2) дисперсию отклика
(3) разность средних значений откликов, соответствующих первому и второму уровням фактора
(4) разность средних значений откликов, соответствующих первому и третьему уровням фактора
(5) разность дисперсий откликов, соответствующих первому и второму уровням фактора
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент ассоциации Юла. Этот коэффициент
и , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент ассоциации Юла. Этот коэффициент
(1) измеряет силу односторонней несимметричной связи между признаками ![math]()
и ![math]()
и
(2) измеряет силу двусторонней симметричной связи между признаками
(3) позволяет на заданном уровне значимости принять решение о зависимости (независимости) признаков ![math]()
и ![math]()
и Коэффициент конкордации Кендалла ![math]()
, где ![math]()
, может принимать значения
, где 
, может принимать значения
(1) ![math]()
(2) ![math]()
(3) ![math]()
Проблема мультиколлинеарности в линейной регрессионной модели обусловлена следующим обстоятельством
(1) наличием линейной зависимости между выходной (результирующей) переменной и входными (объясняющими) переменными
(2) наличием линейной зависимости между входными (объясняющими) переменными
(3) погрешности имеют различные дисперсии
Рассматривается задача двухфакторного дисперсионного анализа. Основная (проверяемая) гипотеза заключается в том, что
(1) главный фактор не оказывает влияния на отклик
(2) мешающий фактор не оказывает влияния на отклик
(3) и главный и мешающий факторы не оказывают влияния на отклик
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана ![math]()
. Полученное значение следует трактовать таким образом:
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана 
. Полученное значение следует трактовать таким образом:
(1) коэффициент корреляции переменных ![math]()
и ![math]()
равен 0.3
и равен 0.3
(2) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков и
(3) прогноз любой категории признака ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков и
(4) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков и
(5) прогноз любой категории признака ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 30%, если при прогнозировании будет учтено совместное распределение признаков и Для двумерной гауссовской выборки ![math]()
вычислен выборочный коэффициент корреляции ![math]()
. Какое распределение имеет статистика ![math]()
в том случае, когда случайные величины ![math]()
и ![math]()
независимы?
вычислен выборочный коэффициент корреляции 
. Какое распределение имеет статистика 
в том случае, когда случайные величины и независимы?
(1) распределение Стьюдента с 15-ю степенями свободы ![math]()
(2) распределение Стьюдента с 13-ю степенями свободы ![math]()
(3) стандартное гауссовское ![math]()
(4) распределение хи-квадрат с 14-ю степенями свободы ![math]()
(5) распределение хи-квадрат с 13-ю степенями свободы ![math]()
У каждого из n объектов измеряется большое количество показателей. Требуется без нарушения существенной структуры данных перейти к пространству показателей меньшей размерности. Такая процедура сжатия возможна
(1) всегда
(2) в случае некоррелированности показателей
(3) в случае сильной коррелированности показателей
Для проверки основной гипотезы в задаче однофакторного дисперсионного анализа применяют F-критерий и ранговый критерий Краскела-Уоллиса. Известно, что наблюдения имеют нормальное распределение, а число уровней фактора равно К. Чему равна в этом случае асимптотическая относительная эффективность по Питмену критерия Краскела- Уоллиса по отношению к F-критерию?
(1) ![math]()
(2) ![math]()
(3) 0.864
(4) ![math]()
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности ![math]()
. Полученный результат можно трактовать следующим образом
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности 
. Полученный результат можно трактовать следующим образом
(1) признаки ![math]()
и ![math]()
независимы
и независимы
(2) признаки ![math]()
и ![math]()
зависимы
и зависимы
(3) этот коэффициент не позволяет сделать вывод о зависимости или независимости признаков ![math]()
и ![math]()
. Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками ![math]()
и ![math]()
слабая
и . Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками и слабая По двумерной гауссовской выборке ![math]()
известного объема n вычислен выборочный коэффициент корреляции ![math]()
. Имея эту информацию, можно
известного объема n вычислен выборочный коэффициент корреляции . Имея эту информацию, можно
(1) на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин ![math]()
и ![math]()
для любого n>3
и для любого n>3
(2) на заданном уровне значимости проверить гипотезу о независимости случайных величин ![math]()
и ![math]()
для любого n>3
и для любого n>3
(3) на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин ![math]()
и ![math]()
только при достаточно большом объеме выборки n
и только при достаточно большом объеме выборки n
(4) на заданном уровне значимости проверить гипотезу о независимости случайных величин ![math]()
и ![math]()
только при достаточно большом объеме выборки n
и только при достаточно большом объеме выборки n Известны парные коэффициенты корреляции случайных величин ![math]()
: ![math]()
Частный коэффициент корреляции случайных величин ![math]()
и ![math]()
при фиксированном значении ![math]()
будет
: 
Частный коэффициент корреляции случайных величин и при фиксированном значении будет
(1) положительным
(2) отрицательным
(3) равным нулю
Откликом в задаче однофакторного дисперсионного анализа называют
(1) значение измеряемого признака
(2) переменную, которая влияет на значение измеряемого признака
(3) погрешность измеряемого признака
Переменная ![math]()
измерена в порядковой шкале. Результаты измерений этой переменной
измерена в порядковой шкале. Результаты измерений этой переменной
(1) можно представить в количественной шкале измерений
(2) можно представить в номинальной шкале измерений
(3) нельзя представить в какой-либо другой шкале измерений
Переменная ![math]()
измерена в номинальной шкале, а переменная ![math]()
- в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
измерена в номинальной шкале, а переменная - в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
(1) преобразовать переменную ![math]()
в номинальную переменную и применить критерий хи-квадрат
в номинальную переменную и применить критерий хи-квадрат
(2) преобразовать переменную ![math]()
в количественную переменную и применить критерий для проверки независимости количественных переменных
в количественную переменную и применить критерий для проверки независимости количественных переменных
(3) применить критерий Колмогорова-Смирнова
Рассматривается модель следующего вида ![math]()
, в которой ![math]()
и ![math]()
– наблюдаемые случайные величины, а ![math]()
- ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и ![math]()
независимы. Корреляционным отношением переменной ![math]()
по ![math]()
называют
, в которой и – наблюдаемые случайные величины, а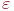 
- ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и 
независимы. Корреляционным отношением переменной по называют
(1) ![math]()
(квадрат коэффициента корреляции переменных ![math]()
и ![math]()
)
(квадрат коэффициента корреляции переменных и )
(2) ![math]()
(3) ![math]()
Количество уровней фактора в задаче однофакторного дисперсионного анализа может быть
(1) любым целым числом ![math]()
(2) любым целым числом ![math]()
(3) любым положительным действительным числом
Переменная ![math]()
измеряется в номинальной шкале и имеет 6 градаций, переменная ![math]()
измеряется в номинальной шкале и имеет 4 градации. Для того чтобы выяснить, являются ли переменные ![math]()
и ![math]()
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
измеряется в номинальной шкале и имеет 6 градаций, переменная измеряется в номинальной шкале и имеет 4 градации. Для того чтобы выяснить, являются ли переменные и зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
(1) 24
(2) 15
(3) 10
(4) 23
В учебной части имеются данные о количестве пропущенных занятий (показатель Х) и успеваемости по дисциплине "Анализ данных" (показатель Y) ста студентов. Коэффициент корреляции Спирмена для переменных ![math]()
и ![math]()
оказался равным -0.7. Эта информация
и оказался равным -0.7. Эта информация
(1) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная положительная связь
и существует монотонная положительная связь
(2) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная отрицательная связь
и существует монотонная отрицательная связь
(3) позволяет сделать вывод о том, что на уровне значимости 0.05 нет оснований для отклонения гипотезы о независимости показателей ![math]()
и ![math]()
и
(4) не позволяет сделать вывод о зависимости или независимости показателей ![math]()
и ![math]()
и МНК-оценка параметра ![math]()
линейной регрессионной модели совпадает с оценкой максимального правдоподобия параметра ![math]()
линейной регрессионной модели совпадает с оценкой максимального правдоподобия параметра
(1) при любом распределении шумов
(2) в том случае, когда шумы имеют гауссовское распределение
(3) в том случае, когда функция плотности распределения шумов является четной
Необходимым условием для применения F-критерия в задаче однофакторного дисперсионного анализа является следующее требование
(1) погрешности имеют стандартное гауссовское распределение
(2) погрешности имеют гауссовское распределение с нулевым математическим ожиданием и одинаковыми дисперсией
(3) погрешности имеют некоторое непрерывное распределение с нулевым математическим ожиданием
Для номинального признака ![math]()
, имеющего 6 градаций, и номинального признака ![math]()
, имеющего 3 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 20.67. Согласно таблицам, квантили распределения хи-квадрат ![math]()
, ![math]()
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
, имеющего 6 градаций, и номинального признака , имеющего 3 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 20.67. Согласно таблицам, квантили распределения хи-квадрат 
, 
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
(1) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть
(2) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует принять
и следует принять
(3) на уровне значимости 0.01 нет оснований для отклонения гипотезы о независимости признаков ![math]()
и ![math]()
и
(4) на уровне значимости 0.01 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть В ходе эксперимента получена реализация двумерной выборки. Известно, что первое наблюдение (7;3) , а второе (3;5). Можно сказать, что эти пары
(1) согласованы
(2) несогласованы
(3) коррелированны
(4) некоррелированны
Рассматривается модель линейной регрессии ![math]()
, ![math]()
, где ![math]()
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения ![math]()
. Для оценивания неизвестных параметров ![math]()
применен метод наименьших модулей (МНМ). Величины дисперсий ![math]()
, полученных МНМ-оценок, зависят от
, , где - ненаблюдаемые центрированные погрешности, имеющие плотность распределения . Для оценивания неизвестных параметров применен метод наименьших модулей (МНМ). Величины дисперсий , полученных МНМ-оценок, зависят от
(1) вида матрицы плана
(2) значения ![math]()
(3) дисперсии погрешностей ![math]()
(4) константы ![math]()
Наблюдения ![math]()
описываются моделью следующего вида ![math]()
, где
![math]()
-неизвестное общее среднее, ![math]()
-отклонение от среднего, вызванное изменением уровня факторной переменной, ![math]()
- погрешности с нулевым математическим ожиданием.
Контраст ![math]()
параметров ![math]()
в этой модели задан следующим образом
![math]()
, где ![math]()
.
Определенный таким образом контраст характеризует
описываются моделью следующего вида , где
-неизвестное общее среднее, -отклонение от среднего, вызванное изменением уровня факторной переменной, - погрешности с нулевым математическим ожиданием.
Контраст параметров в этой модели задан следующим образом
, где 
.
Определенный таким образом контраст характеризует
(1) среднее значение отклика
(2) дисперсию отклика
(3) разность средних значений откликов, соответствующих первому и второму уровням фактора
(4) разность средних значений откликов, соответствующих первому и третьему уровням фактора
(5) разность дисперсий откликов, соответствующих первому и третьему уровням фактора
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент контингенции. Этот коэффициент
и , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент контингенции. Этот коэффициент
(1) измеряет силу односторонней несимметричной связи между признаками ![math]()
и ![math]()
и
(2) измеряет силу двусторонней симметричной связи между признаками
(3) позволяет на заданном уровне значимости принять решение о зависимости (независимости) признаков ![math]()
и ![math]()
и Для группы из ![math]()
экспертов вычислен коэффициент конкордации Кендалла ![math]()
. Значение ![math]()
близкое к единице нужно трактовать следующим образом:
экспертов вычислен коэффициент конкордации Кендалла . Значение близкое к единице нужно трактовать следующим образом:
(1) данная группа экспертов не обладает единой системой предпочтений
(2) данная группа экспертов обладает единой системой предпочтений
(3) имея эту информацию, нельзя сделать каких-либо содержательных выводов о согласованности экспертной группы
К каким последствиям может привести наличие мультиколлинеарности в линейной регрессионной модели?
(1) существенному изменению оценок регрессионных параметров при незначительном изменении матрицы плана
(2) смещенности оценок параметров регрессии
(3) большим дисперсиям оценок регрессионных параметров
Необходимым условием применения критерия Пейджа в задаче двухфакторного дисперсионного анализа является
(1) гауссовость наблюдений
(2) априорная информация о том, что при увеличении уровня главного фактора среднее значение отклика будет увеличиваться
(3) априорная информация о том, что при увеличении уровня мешающего фактора среднее значение отклика будет увеличиваться
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана ![math]()
. Полученное значение следует трактовать таким образом:
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана 
. Полученное значение следует трактовать таким образом:
(1) коэффициент корреляции переменных ![math]()
и ![math]()
равен 0.4
и равен 0.4
(2) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков и
(3) прогноз любой категории признака ![math]()
будет улучшен на 40%, если при прогнозировании учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 40%, если при прогнозировании учтено совместное распределение признаков и
(4) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков и
(5) прогноз любой категории признака ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 40%, если при прогнозировании будет учтено совместное распределение признаков и Для двумерной гауссовской выборки ![math]()
вычислен выборочный коэффициент корреляции ![math]()
. Какое распределение имеет статистика ![math]()
в том случае, когда случайные величины ![math]()
и ![math]()
независимы?
вычислен выборочный коэффициент корреляции . Какое распределение имеет статистика 
в том случае, когда случайные величины и независимы?
(1) распределение Стьюдента с 10-ю степенями свободы ![math]()
(2) распределение Стьюдента с 12-ю степенями свободы ![math]()
(3) стандартное гауссовское ![math]()
(4) распределение хи-квадрат с 10-ю степенями свободы ![math]()
(5) распределение хи-квадрат с 11-ю степенями свободы ![math]()
Вектор показателей ![math]()
требуется наилучшим образом описать вектором общих факторов ![math]()
размерности ![math]()
. Новые показатели ![math]()
должны удовлетворять следующему условию
требуется наилучшим образом описать вектором общих факторов 
размерности 
. Новые показатели 
должны удовлетворять следующему условию
(1) ![math]()
при ![math]()
при 
(2) ![math]()
при ![math]()
при
(3) ![math]()
, при ![math]()
, при 
Для проверки основной гипотезы в задаче двухфакторного дисперсионного анализа применяют F-критерий и ранговый критерий Фридмана. Известно, что наблюдения имеют нормальное распределение, количество уровней главного фактора равно k, а количество уровней мешающего фактора равно n. Чему равна в этом случае асимптотическая относительная эффективность по Питмену критерия Фридмана по отношению к F-критерию?
(1) ![math]()
(2) ![math]()
(3) 0.864
(4) ![math]()
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент Крамера ![math]()
. Полученный результат можно трактовать следующим образом
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент Крамера 
. Полученный результат можно трактовать следующим образом
(1) признаки ![math]()
и ![math]()
независимы
и независимы
(2) признаки ![math]()
и ![math]()
зависимы
и зависимы
(3) этот коэффициент не позволяет сделать вывод о зависимости или независимости признаков ![math]()
и ![math]()
. Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками ![math]()
и ![math]()
слабая
и . Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками и слабая По двумерной выборке ![math]()
, соответствующей некоторому распределению ![math]()
, вычислен выборочный коэффициент корреляции ![math]()
. Объем выборки n известен. Имея эту информацию, можно
, соответствующей некоторому распределению 
, вычислен выборочный коэффициент корреляции . Объем выборки n известен. Имея эту информацию, можно
(1) на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин ![math]()
и ![math]()
для любого n>3
и для любого n>3
(2) на заданном уровне значимости проверить гипотезу о независимости случайных величин ![math]()
и ![math]()
для любого n>3
и для любого n>3
(3) на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин ![math]()
и ![math]()
только при достаточно большом объеме выборки n
и только при достаточно большом объеме выборки n
(4) на заданном уровне значимости проверить гипотезу о независимости случайных величин ![math]()
и ![math]()
только при достаточно большом объеме выборки n
и только при достаточно большом объеме выборки n Известны парные коэффициенты корреляции случайных величин ![math]()
: ![math]()
Частный коэффициент корреляции случайных величин ![math]()
и ![math]()
при фиксированном значении ![math]()
будет
: 
Частный коэффициент корреляции случайных величин и при фиксированном значении будет
(1) положительным
(2) отрицательным
(3) равным нулю
Уровнем фактора в задаче однофакторного дисперсионного анализа называют
(1) значение измеряемого признака
(2) переменную, которая влияет на значение измеряемого признака
(3) конкретную реализацию фактора
Переменная ![math]()
измерена в номинальной шкале. Результаты измерений этой переменной
измерена в номинальной шкале. Результаты измерений этой переменной
(1) можно представить в количественной шкале измерений
(2) можно представить в порядковой шкале измерений
(3) нельзя представить в какой-либо другой шкале измерений
Признаки ![math]()
и ![math]()
измерены в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
и измерены в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
(1) преобразовать обе переменные в номинальные переменные и применить критерий хи-квадрат
(2) преобразовать обе переменные в порядковые переменные и применить ранговый критерий Спирмена
(3) применить критерий Колмогорова-Смирнова
Коэффициент множественной корреляции ![math]()
между выходной (результирующей) переменной ![math]()
и входными (объясняющими) переменными ![math]()
обладает следующими свойствами
между выходной (результирующей) переменной и входными (объясняющими) переменными 
обладает следующими свойствами
(1) ![math]()
(2) ![math]()
(3) ![math]()
(4) ![math]()
(5) если ![math]()
, то ![math]()
, то 
Основная (проверяемая) гипотеза в задаче однофакторного дисперсионного анализа состоит в том, что
(1) неизвестные средние значения наблюдений одинаковы при различных уровнях фактора
(2) неизвестные дисперсии наблюдений одинаковы при различных уровнях фактора
(3) ненаблюдаемые погрешности имеют одинаковое распределение при различных уровнях фактора
Переменная ![math]()
измеряется в номинальной шкале и имеет 3 градаций, переменная ![math]()
измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные ![math]()
и ![math]()
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
измеряется в номинальной шкале и имеет 3 градаций, переменная измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные и зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
(1) 2
(2) 5
(3) 6
Сто(100) студентов-математиков прошли тестирование по математическому анализу (показатель Х) и английскому языку (показатель Y). Коэффициент корреляции Спирмена для переменных ![math]()
и ![math]()
оказался равным 0.4. Эта информация
и оказался равным 0.4. Эта информация
(1) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная положительная связь
и существует монотонная положительная связь
(2) позволяет на уровне значимости 0.05 сделать вывод о том, что между показателями ![math]()
и ![math]()
существует монотонная отрицательная связь
и существует монотонная отрицательная связь
(3) позволяет сделать вывод о том, что на уровне значимости 0.05 нет оснований для отклонения гипотезы о независимости показателей ![math]()
и ![math]()
и
(4) не позволяет сделать вывод о зависимости или независимости показателей ![math]()
и ![math]()
и Пусть ![math]()
- МНК-оценка неизвестного регрессионного параметра ![math]()
, ![math]()
- любая несмещенная оценка этого параметра, а ![math]()
- некоторый детерминированный вектор. Неравенство ![math]()
выполняется
- МНК-оценка неизвестного регрессионного параметра , 
- любая несмещенная оценка этого параметра, а 
- некоторый детерминированный вектор. Неравенство 
выполняется
(1) всегда
(2) в том случае, когда функция плотности распределения шумов является четной и шумы имеют конечную дисперсию
(3) в том случае, когда шумы имеют гауссовское распределение
Необходимым условием для применения критерия Краскела-Уоллиса в задаче однофакторного дисперсионного анализа является следующее требование
(1) погрешности имеют стандартное гауссовское распределение
(2) погрешности имеют гауссовское распределение с нулевым математическим ожиданием и дисперсией ![math]()
(3) погрешности имеют некоторое непрерывное распределение с нулевым математическим ожиданием
Для номинального признака ![math]()
, имеющего 4 градаций, и номинального признака ![math]()
, имеющего 6 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 26.07. Согласно таблицам квантили распределения хи-квадрат ![math]()
, ![math]()
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
, имеющего 4 градаций, и номинального признака , имеющего 6 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 26.07. Согласно таблицам квантили распределения хи-квадрат 
, 
.
Какой (какие) выводы можно сделать, опираясь на полученный результат?
(1) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть
(2) на уровне значимости 0.05 гипотезу о независимости признаков ![math]()
и ![math]()
следует принять
и следует принять
(3) на уровне значимости 0.01 нет оснований для отклонения гипотезы о независимости признаков ![math]()
и ![math]()
и
(4) на уровне значимости 0.01 гипотезу о независимости признаков ![math]()
и ![math]()
следует отвергнуть
и следует отвергнуть В ходе эксперимента получена реализация двумерной выборки. Известно, что первое наблюдение (10;3) , а второе (3;1). Можно сказать, что эти пары
(1) согласованы
(2) несогласованы
(3) коррелированны
(4) некоррелированны
Рассматривается модель линейной регрессии ![math]()
, ![math]()
, где ![math]()
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения ![math]()
. Для оценивания неизвестных параметров ![math]()
применен ранговый метод. Величины дисперсий ![math]()
, полученных R-оценок, зависят от
, , где - ненаблюдаемые центрированные погрешности, имеющие плотность распределения . Для оценивания неизвестных параметров применен ранговый метод. Величины дисперсий , полученных R-оценок, зависят от
(1) вида матрицы плана
(2) значения ![math]()
(3) дисперсии погрешностей ![math]()
(4) константы ![math]()
Наблюдения ![math]()
описываются моделью следующего вида ![math]()
, где
![math]()
-неизвестное общее среднее, ![math]()
-отклонение от среднего, вызванное изменением уровня факторной переменной, ![math]()
- погрешности с нулевым математическим ожиданием.
Контраст ![math]()
параметров ![math]()
в этой модели задан следующим образом
![math]()
, где ![math]()
.
Определенный таким образом контраст характеризует
описываются моделью следующего вида , где
-неизвестное общее среднее, -отклонение от среднего, вызванное изменением уровня факторной переменной, - погрешности с нулевым математическим ожиданием.
Контраст параметров в этой модели задан следующим образом
, где 
.
Определенный таким образом контраст характеризует
(1) среднее значение отклика
(2) дисперсию отклика
(3) разность средних значений откликов, соответствующих первому и второму уровням фактора
(4) разность средних значений откликов, соответствующих второму и третьему уровням фактора
(5) разность дисперсий откликов, соответствующих второму и третьему уровням фактора
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислена статистика хи-квадрат. Эта статистика
и , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислена статистика хи-квадрат. Эта статистика
(1) измеряет силу односторонней несимметричной связи между признаками ![math]()
и ![math]()
и
(2) измеряет силу двусторонней симметричной связи между признаками
(3) позволяет на заданном уровне значимости принять решение о зависимости (независимости) признаков ![math]()
и ![math]()
и Коэффициент согласованности Кендалла ![math]()
для двух выборок может принимать значения
для двух выборок может принимать значения
(1) ![math]()
(2) ![math]()
(3) ![math]()
Какой (какие) из нижеперечисленных фактов свидетельствует о наличии мультиколлинеарности в линейной регрессионной модели?
(1) в корреляционной матрице входных (объясняющих) переменных есть значения, модуль которых близок к единице
(2) корреляционная матрица входных (объясняющих) переменных является диагональной
(3) коэффициент детерминации близок к единице
(4) матрица ![math]()
(![math]()
- матрица плана) имеет высокий показатель обусловленности ![math]()
, ![math]()
- собственные значения матрицы ![math]()
(
- матрица плана) имеет высокий показатель обусловленности 
, 
- собственные значения матрицы Необходимым условием применения F-критерия в задаче двухфакторного дисперсионного анализа является следующее требование
(1) погрешности имеют стандартное гауссовское распределение
(2) погрешности имеют гауссовское распределение с нулевым математическим ожиданием
(3) погрешности имеют распределение Стьюдента
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана ![math]()
. Полученное значение следует трактовать таким образом:
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана 
. Полученное значение следует трактовать таким образом:
(1) коэффициент корреляции переменных ![math]()
и ![math]()
равен 0.2
и равен 0.2
(2) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков и
(3) прогноз любой категории признака ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков и
(4) прогноз модальной (наиболее вероятной) категории признака ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков и
(5) прогноз любой категории признака ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков ![math]()
и ![math]()
будет улучшен на 20%, если при прогнозировании будет учтено совместное распределение признаков и Для двумерной гауссовской выборки ![math]()
вычислен выборочный коэффициент корреляции ![math]()
. Какое распределение имеет статистика ![math]()
в том случае, когда случайные величины ![math]()
и ![math]()
независимы?
вычислен выборочный коэффициент корреляции . Какое распределение имеет статистика 
в том случае, когда случайные величины и независимы?
(1) распределение Стьюдента с 14-ю степенями свободы ![math]()
(2) распределение Стьюдента с 12-ю степенями свободы ![math]()
(3) стандартное гауссовское ![math]()
(4) распределение хи-квадрат с 14-ю степенями свободы ![math]()
(5) распределение хи-квадрат с 13-ю степенями свободы ![math]()
Вектор показателей ![math]()
представлен в виде ![math]()
,где F- вектор общих факторов размерности ![math]()
, ![math]()
- вектор случайных погрешностей размерности k, А - матрица нагрузок размерности ![math]()
. Элементы ![math]()
,![math]()
![math]()
матрицы А - это
представлен в виде 
,где F- вектор общих факторов размерности , - вектор случайных погрешностей размерности k, А - матрица нагрузок размерности 
. Элементы 
,
матрицы А - это
(1) ![math]()
(2) ![math]()
(3) ![math]()
Для проверки основной гипотезы в задаче двухфакторного дисперсионного анализа применяют F-критерий и ранговый критерий Фридмана. Асимптотическая относительная эффективность по Питмену критерия Фридмана по отношению к F-критерию зависит от
(1) распределения наблюдений
(2) количества уровней главного фактора
(3) количества уровней мешающего фактора
Для признаков ![math]()
и ![math]()
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности ![math]()
. Полученный результат можно трактовать следующим образом
и , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности 
. Полученный результат можно трактовать следующим образом
(1) признаки ![math]()
и ![math]()
независимы
и независимы
(2) признаки ![math]()
и ![math]()
зависимы
и зависимы
(3) этот коэффициент не позволяет сделать вывод о зависимости или независимости признаков ![math]()
и ![math]()
. Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками ![math]()
и ![math]()
умеренная
и . Однако, если вычисленное значение статистики хи-квадрат попадает в критическую область, то можно сказать, что сила связи между признаками и умеренная
(4) этот коэффициент не позволяет сделать вывод о зависимости или независимости признаков ![math]()
и ![math]()
. Однако, если вычисленное значение статистики хи-квадрат попадает в
критическую область, то можно сказать, что сила связи между признаками ![math]()
и ![math]()
слабая
и . Однако, если вычисленное значение статистики хи-квадрат попадает в
критическую область, то можно сказать, что сила связи между признаками и слабая Известно, что коэффициент корреляции случайных величин ![math]()
и ![math]()
равен нулю. Это означает, что
и равен нулю. Это означает, что
(1) линейная связь между случайными величинами ![math]()
и ![math]()
отсутствует
и отсутствует
(2) случайные величины ![math]()
и ![math]()
линейно зависимы
и линейно зависимы
(3) случайные величины ![math]()
и ![math]()
зависимы
и зависимы
(4) случайные величины ![math]()
и ![math]()
независимы
и независимы
(5) если случайный вектор ![math]()
является гауссовским, то случайные величины ![math]()
и ![math]()
независимы
является гауссовским, то случайные величины и независимы