Главная / Алгоритмы и дискретные структуры / Введение в теорию графов

Введение в теорию графов - ответы на тесты Интуит

Правильные ответы выделены зелёным цветом.
Все ответы: Приводятся начальные сведения о графах, основные понятия и определения, способы представления графов. Рассматриваются основные операции над графами, такие как - объединение, пересечение, кольцевая сумма, удаление вершины, удаление ребра, замыкание и стягивание.
Какого типа граф изображен на рисунке?files
(1) орграф
(2) граф
(3) смешанный граф
Выполнить операцию объединения G1 G2 для графов, показанных на рисунке 1files files files
(1) граф представлен на рис.2 а
(2) граф представлен на рис.2 б
(3) граф представлен на рис.2 в
(4) нет верного рисунка
Найти прямые отображения для вершин х1 и х2 графа, показанного на рисунке files
(1) Г+1 (х1) = {х1, х2, х3, х4}, Г+1 (х2) = {х1, х3 }
(2) Г+1 (х1) = { х2, х3, х4}, Г+1 (х2) = {х1, х3 }
(3) Г+1 (х1) = { х3, х1, х2}, Г+1 (х2) = {х3, х1 }
Для графа, представленного на рисунке 1 построить матрицу достижимости Rfiles
а
X1X2X3X4X5
X111111
R=X200111
X300110
X400010
X500011
б
X1X2X3X4X5
X111111
R=X200111
X300010
X400000
X500010
в
X1X2X3X4X5
X111111
R=X201111
X300110
X400010
X500011
(1) б
(2) а
(3) в
Какие из приведенных на рисунке графов являются полными? files
(1) а, с
(2) а, с, d
(3) c
Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его подграфами?files files
(1) а
(2) b
(3) с
(4) d
(5) e
(6) f
Методом Мальгранжа разбить граф, представленный ниже матрицей смежности, на подграфы
X1X2X3X4X5X6X7X8
X111010000
X210100010
X300001000
X400100000
X500010000
X600000000
X701000101
X810000000
(1) G1={x1, x2 , х7, х8 }, G2 = { х3, х4, х5 }, G3 ={х6}
(2) G1={x1, x2 , х7, х8 }, G2 = { х3, х4 }, G3 ={ х5 ,х6}
(3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7, х8 }
Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин A и E.files
(1) A →​ B →​ B, A →​ В →​ C, E →​ F →​ A, E →​ B →​ B, E →​ B →​ C, E →​ F →​ D
(2) A →​ В →​ C, E →​ F →​ A, E →​ B →​ C, E →​ F →​ D
(3) A →​ В →​ C, E →​ F →​ A, E →​ B →​ B, E →​ B →​ C, E →​ F →​ D
Обновление пометок происходит по формуле:
(1) L(хi) = min [ L(хi), L(p) + C(p, хi) ]
(2) L(хi) = min [ L(хi), L(p) - C(p, хi) ]
(3) L(хi) = min [ L(хi), C(p, хi) ]
Какие вершины инцидентны дуге f в графе на рисунке?files
(1) 2
(2) 1, 2, 3
(3) 2, 3
Выполнить операцию объединения G1 ∪ G2 для графов, представленных матрицами смежности в таблице 1
Матрица смежности G1
X1X2X3X4X5
X100001
X210010
X300000
X400100
X501010
Матрица смежности G2
X1X2X3X4X5
X100001
X210101
X300000
X401101
X500000
a
X1X2X3X4X5
X100001
X210000
X300000
X400100
X500000
б
X1X2X3X4X5
X100000
X200111
X300000
X401001
X501010
в
X1X2X3X4X5
X100001
X210111
X300000
X401101
X501010
(1) граф представлен б
(2) граф представлен а
(3) граф представлен в
Найти обратные отображения для вершин х3 и х4 графа, показанного на рисунке files
(1) Г-1 (х3) = {х6, х4 }, Г–1 (х4) ={х1, х3 }
(2) Г–1 (х3) = {х2, х3 }, Г–1 (х4) ={х1, х3 , х4}
(3) Г–1 (х3) = {х1, х2 }, Г–1 (х4) ={х1, х3 , х4}
Для графа, приведенного на рисунке 1, найти матрицу контрдостижимости.files
а
X1X2X3X4X5
X110000
Q=X211000
X311100
X410111
X511001
б
X1X2X3X4X5
X110000
Q=X211000
X311100
X411111
X511001
в
X1X2X3X4X5
X110000
Q=X211000
X311100
X411110
X511001
(1) а
(2) в
(3) б
По матрицам смежности, приведенным ниже определить какие из графов являются полными.
а
1111
0011
0001
1111
b
0101
0001
0010
1010
c
1011
1101
0111
1111
d
0000
1000
1100
1110
(1) а, c, d
(2) a, с
(3) d
Для графа G = (X, A), представленного на рисунке 1, описать матрицей смежности порожденный подграф {х1,х2,х3,х4,х5}files
а
X1X2X3X4X5
X101000
X200101
X300001
X400100
X500100
b
X1X2X3X4X5
X101000
X200101
X300011
X400010
X500110
c
X1X2X3X4X5
X101000
X200101
X300011
X400000
X500100
(1) c
(2) b
(3) а
Методом Мальгранжа разбить граф, представленный на рисунке, на максимальные сильно связные подграфыfiles
(1) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х4, х7, х8 }
(2) G1={x1, x2 , х8 }, G2 = { х3, , х7, х5 }, G3 ={х6 , х4}
(3) G1={x1, x2 , х3, х5 , х7, х8 }, G2 ={ х4 , х6}
Построить орцепи максимальной длины из вершин A и B графа, изображенного на рисунке files
(1) (A, B) →​ (B, C), (B, С)
(2) (A, B) →​ (B, C), (B, B) →​ (B, C)
(3) (A, B) →​ (B, B) →​ (B, C), (B, B) →​ (B, C)
Для нахождения кратчайшего пути от s к хi, предшествующую вершину xi* можно найти как одну из вершин, для которой
(1) L(xi*)-c(xi*)=L(xi)
(2) L(xi*) c(xi*)=L(xi)
(3) L(xi*) + c(xi*)=L(xi* xi)
Какие дуги инцидентны вершине 3 в графе на рисунке?files
(1) a
(2) a, e, f
(3) d, e, f
Для графа G1, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х1,х2). Верно ли результат представлен матрицей смежности ниже? files
X(1,2)X3X4X5
X(1,2)111
X3
X41
X511
(1) неверно
(2) верно
Найти прямые многозначные отображения 4-го порядка для вершин х1 и х2 графа, показанного на рисунке files
(1) Г+4(х1) ={ х1, х2, х3, х4, х5, х6}, Г+4(х2) ={ х1,х3, х4, х5, х6}
(2) Г+4(х1) ={ х2, х3, х4, х5, х6}, Г+4(х2) ={ х1, х2, х3, х4, х5, х6}
(3) Г+4(х1) ={ х1, х2, х3, х4, х5, х6}, Г+4(х2) ={ х1, х2, х3, х4, х5, х6}
Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х1 и х7.files
(1) {х1, х2, х3, х4 }
(2) {х1, х2, х4, х7}
(3) { х1, х2, х3, х4, х7}
Какие из приведенных на рисунке графов являются симметрическими?files
(1) a
(2) a, с
(3) а, c, d
Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где xi,xj ∈ A' тогда и только тогда, когда i+j нечетно files
(1) G = (Х, А), где Х = {хi}, i = 1, 2, …, 8 – множество вершин; А = {ai }, i = 1, 2, ..., 7 – множество дуг, причем А = {(х1, х2), (х4, х7), (х2, х4 ), (х2, х3), (х3, х8), (х4 , х1), (х7 , х6), }
(2) G = (Х, А), где Х = {хi}, i = 1, 2, …,8 – множество вершин; А = {ai }, i = 1, 2, ... – множество дуг, причем А = {(х1, х2), (х2, х3), (х2, х5 ), (х2, х7), (х3, х4), (х8 , х7), (х7 , х6), (х3, х6), (х5 , х7), (х7 , х6) }
(3) G = (Х, А), где Х = {хi}, i = 1, 2, …,8 – множество вершин; А = {ai }, i = 1, 2, ..., 7– множество дуг, причем А = {(х1, х2), (х2, х3), (х2, х5 ), (х3, х4), (х1, х8), (х8 , х7), (х7 , х6), }
Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного на рисункеfiles
(1) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х4, х7, х8 }
(2) G1={x1, x2 , х8 }, G2 = { х3, , х7, х5 }, G3 ={х6 , х4}
(3) G1={x1, x2 , х7, х8 }, G2 ={ х4, х3, х5} G3 ={ х6}
Построить простые орцепи максимальной длины из вершин A и B графа, изображенного на рисунке files
(1) (A, B) →​ (B, B) →​ (B, C), (B, C)
(2) (A, B) →​ (B, B) →​ (B, C), (B, B) →​ (B, C)
(3) (A, B) →​ (B, C), (B, C)
Найти кратчайший путь от вершины 1 к вершине 5 графа, представленного на рисунке files
(1) 12
(2) 15
(3) 16
Перечислите дуги, являющиеся петлями в графе на рисунке?files
(1) a, c
(2) c, a, d, e
(3) d, e
Для графа G2, показанном на рисунке 1, выполнить операцию стягивания двух вершин (х1,х2). Верно ли результат представлен матрицей смежности ниже?files
X(1,2)X3X4X5
X(1,2)11
X3
X4111
X5
(1) неверно
(2) верно
Найти обратные многозначные отображения 3-го порядка для вершин х3и х4графа, показанного на рисунке files
(1) Г-3(х3)={х1, х4 }, Г-3(х4) = {х2, х4 }
(2) Г-3(х3)={х1, х4 }, Г-3(х4) =
(3) Г-3(х3)={х2, х4 }, Г-3(х4) =
Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 2. files
(1) между F и A
(2) между D и B
(3) между E и C
Какие из приведенных на рисунке графов являются антисимметрическими? files
(1) а, b, d
(2) a, с
(3) b
Найти максимальный сильно связанный подграф, включающий вершину C, для графа, матрица смежности которого представлена ниже
ABCDEFGK
A11001000
B00101100
C00101000
D00000001
E00000100
F10000010
G00000001
K00010000
(1) Gмсс={ B, C, E, F}
(2) Gмсс={A, B, C, E, F}
(3) Gмсс={A, B, C, F}

Для графа на рисунке даны маршруты из вершины A в вершину F:files

a) (A, B), (B, C), (C, G), (G, F)

b) (A, K), (K, H), (H, F)

c) (A, C), (C, E), (E, D), (D, C), (C, H), (H, F)

d) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

Найти среди них цепи

(1) a, b
(2) a, b, c
(3) a, b, c, d
Найти кратчайший путь от вершины x1 к вершине x5 графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис.Б files
(1) 13
(2) 19
(3) 18
Найдите полустепени исхода и захода для вершины х2 графаfiles
(1) d0(х2)=3, dt(х2)=2
(2) d0(х2)=2, dt(х2)=2
(3) d0(х2)=2, dt(х2)=1
В графе G6 , показанном на рис. 1 удалить вершину х1. Результат представлен ниже в матричном видеfiles
а
X2X3
X201
X310
б
X1X2
X101
X210
в
X1X3
X101
X310
(1) верно б
(2) верно а
(3) верно в
Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х1и х2,files
(1) Т+(х1) = { х1, х2, х3, х5, х6}, Т+( х2) ={ х1, х2, х3, х4, х5, х6}
(2) Т+(х1) = { х1, х2, х3, х5, х6}, Т+( х2) ={ х1, х2, х3, х5, х6}
(3) Т+(х1) = { х1, х2, х3, х4, х5, х6}, Т+( х2) ={ х1, х2, х3, х4, х5, х6}
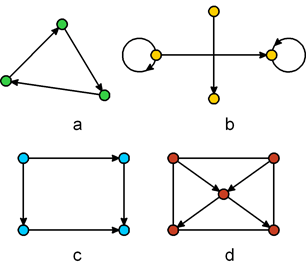
Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 3.files
(1) между D и B
(2) между A и D
(3) между A и C
Какие из приведенных на рисунке графов являются антисимметрическими?files
(1) a
(2) b
(3) c
(4) d
Какие из приведенных на рисунке графов являются сильно связными?files
(1) a, d, e
(2) a, d
(3) d

На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна. files

Скорость оборота капитала n -го пути судна найдем как суммарную выгоду пути, деленную на суммарное время, т. е.

vn=∑ ai/ ∑ bi

  • A →​ B →​ C →​ D →​ E →​ A
  • A →​ B →​ C →​ E →​ D →​ A.
  • A →​ D →​ B →​ C →​ E →​ A.
  • A →​ C →​ E →​ D →​ B →​ A.
    • (1) 3
    (2) 1
    (3) 2
    (4) 4
    Для графа, представленного на рисунке 1а, построить базу относительно вершины х1.filesfiles
    (1) рис. 2a
    (2) рис. 2b
    (3) рис. 2c
    Для графа, изображенного на рисунке, дать описание перечислением.files
    (1) G4=(Х, А) , где Х = { хi }, i = 1, 2, 3,4 – множество вершин; А = { ai }, i = 1, 2, ..., 5 множество дуг, причем А = {(х2, х1), (х4, х1), (х3, х1), (х2, х4) }
    (2) G=(Х, А) , где Х = { хi }, i = 1, 2, 3,4 – множество вершин; А = { ai }, i = 1, 2, ..., 5 множество дуг, причем А = {(х2, х1), (х4, х1), (х3, х1), (х2, х4) }
    (3) G=(Х, А) , где Х = { хi }, i = 1, 2, 3,4 – множество вершин; А = { ai }, i = 1, 2, ..., 5 множество дуг, причем А = {(х2, х1), (х4, х1), (х3, х1), (х2, х4), (х3, х3) }
    В графе G6 , показанном на рис. 1 удалить дугу (х3,х2). Результат представлен в матричном виде ниже files
    а
    X1X2X3
    X111
    X211
    X31
    б
    X1X2X3
    X11
    X211
    X311
    в
    X1X2X3
    X11
    X211
    X311
    (1) верно б
    (2) верно а
    (3) верно в
    Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х5и х6,files
    (1) Т-(х5) ={ х1, х2, х4}, Т-(х6) = { х1, х2, х4, х5, х6}
    (2) Т-(х5) ={ х1, х2, х4, х5 }, Т-(х6) = { х1, х2, х4, х5, х6}
    (3) Т-(х5) ={ х1, х2, х4, х5 }, Т-(х6) = { х1, х2, х4, х5}
    Для графа, данного на рисунке найти количество путей длиной 4 между всеми вершинами графаfiles
    (1) 14
    (2) 24
    (3) 15
    Является ли граф на рисунке двудольнымfiles
    (1) да
    (2) нет
    Выделить в графе на рисунке с сильную компоненту, содержащую максимальное число элементов. files
    (1) < х2, х3, х4, х5 >
    (2) < х2, х4, х5 >
    (3) < х4, х5 >
    files

    Для графа, представленного на рисунке даны замкнутые пути:

    М1: (х2, х3), (х3, х4), (х4, х7), (х7, х2)

    М2: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2) (х2, х3), (х3, х7), (х7, х2)

    М3: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2)

    М4: (х3, х4), (х4, х5), (х5, х7), (х7, х3)

    М5: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х1)

    М6: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6) (х6, х1)

    М7: (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6), (х6, х1), (х1, х2)

    Какие из этих путей являются контурами?

    (1) контурами являются: M1, M2,M3, М4, М5, М6, М7
    (2) контурами являются: M1, M3, М4, М5, М6, М7
    (3) контурами являются: M1, M2, М4, М5, М6
    Для графа, представленного на рисунке, дана матрица смежности. Верно ли представлен граф?files
    матрица смежности
    X1X2X3X4
    X11100
    X20011
    X30000
    X41110
    (1) не верно
    (2) верно
    Является ли граф, представленный на рисунке, планарным? files
    (1) нет
    (2) да
    Выделить в графе на рисунке b одностороннюю компоненту, содержащую максимальное число элементов. files
    (1) < х2, х3, х5 >
    (2) < х1, х2, х5 >
    (3) < х1, х2, х3, х5 >
    Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы. files
    (1) эйлеров цикл –(F, C), (C, A), (A, F), (F, E), (E, D), (D, C), (C, B), (B, D) или (D, C), (C, B), (B, D), (D, E), (E, F), (F, C), (C, A), (A, F)
    (2) гамильтонов цикл :(A, C), (C, B), (B, D), (D, E), (E, F), (F, A); эйлеров цикл отсутствует
    (3) гамильтонов цикл отсутствует, эйлеров цикл отсутствует
    По матрице смежности, данной ниже подсчитать количество петель графа.
    101100
    010101
    000101
    001001
    100000
    010001
    (1) петель нет
    (2) 3
    (3) 2
    Для графа на рисунке найти сильную компоненту, содержащую элемент х1files
    (1) G1 = {х1, х2}
    (2) G1 = {х1, х2, х8 }
    (3) G1 = {х1, х7, х8 }
    По матрице инциденций найти полустепени исхода для Х2
    a1a2a3a4a5a6a7a8a9a10
    X11-110101000
    X201-11000000
    X3000-1-110100
    X4000000-1-110
    X500000000-1-1
    X600000-10001
    (1) d0(х2)=3
    (2) d0(х2)=1
    (3) d0(х2)=2
    Является ли граф, изображенный на рисунке орграфом?files
    (1) не является
    (2) является
    (3) это смешанный граф
    Выполнить операцию пересечения G1 G2 для графов, показанных на рисунке 1 files files files
    (1) граф представлен на рис.2 в
    (2) граф представлен на рис.2 б
    (3) граф представлен на рис.2 а
    Найти прямые отображения для вершин х3 и х4 графа, показанного на рисунке files
    (1) Г+1 (х3) = {х4, х6 }, Г+1 (х4) = {х5 }
    (2) Г+1 (х3) = {х4, х6 }, Г+1 (х4) = {х5, х4}
    (3) Г+1 (х3) = {х1, х2 }, Г+1 (х4) = {х5, х4}
    Какая из представленных матриц достижимости соответствует графу на рисунке 1?
    а
    X1X2X3X4X5X6
    X1000111
    R=X2101111
    X3100111
    X4100011
    X5100101
    X6100110
    б
    X1X2X3X4X5X6
    X1100111
    R=X2111111
    X3101111
    X4100111
    X5100111
    X6100111
    в
    X1X2X3X4X5X6
    X1111111
    R=X2010000
    X3011000
    X4111111
    X5111111
    X6111111
    files
    (1) а
    (2) б
    (3) в
    Какие из приведенных на рисунке графов являются полными?files
    (1) а, b, d
    (2) а, b
    (3) b и d
    Дан граф на рисунке 1. Какие из приведенных на рисунке 2 графов являются его остовными подграфами?filesfiles
    (1) а, с, d, e, f
    (2) а, e
    (3) все
    Методом Мальгранжа разбить граф, представленный ниже матрицей смежности, на подграфы
    X1X2X3X4X5X6X7
    X11101000
    X21010010
    X30000100
    X40010000
    X50001000
    X60100001
    X71000000
    (1) G1={x1, x2 , х7}, G2 = { х3, х4 }, G3 ={ х5 ,х6}
    (2) G1={x1, x2 , х7, х6 }, G2 = { х3, х4, х5 }
    (3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7 }
    Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вершин A и D.files
    (1) A →​ В →​ C, D →​ E →​ F, D →​ F →​ D
    (2) A →​ B →​ B, A →​ В →​ C, D →​ E →​ F, D →​ F →​ D, D →​ F →​ A, D →​ E →​ B
    (3) A →​ В →​ C, D →​ E →​ F
    Для чего использую алгоритм Дейкстра?
    (1) для поиска максимального сильного подграфа
    (2) для поиска кратчайших путей
    (3) для поиска вершин графа, имеющих нечетную степень
    (4) для построения матрицы смежности
    Какие вершины инцидентны дуге d в графе на рисунке?files
    (1) 1, 3
    (2) 1, 2, 3
    (3) 2
    Выполнить операцию пересечения G1 ∩ G2 для графов, представленных матрицами смежности в таблице 1
    Матрица смежности G1
    X1X2X3X4X5
    X100001
    X210010
    X300000
    X400100
    X501010
    Матрица смежности G2
    X1X2X3X4X5
    X100001
    X210101
    X300000
    X401101
    X500000
    a
    X1X2X3X4X5
    X100001
    X210000
    X300000
    X400100
    X500000
    б
    X1X2X3X4X5
    X100000
    X200111
    X300000
    X401001
    X501010
    в
    X1X2X3X4X5
    X100001
    X210111
    X300000
    X401101
    X501010
    (1) граф представлен б
    (2) граф представлен а
    (3) граф представлен в
    Найти обратные отображения для вершин х5и х6графа, показанного на рисунке files
    (1) Г–1 (х5) = { х6, х4}, Г–1 (х6) = { х3 ,х6 }
    (2) Г–1 (х5) = { х6, х4}, Г–1 (х6) = { х3},
    (3) Г–1 (х5) = { х6, х4}, Г–1 (х6) = { х6, х4}
    Какая из представленных матриц контрдостижимости соответствует графу на рис. 1?
    а
    X1X2X3X4X5X6
    X1000111
    Q=X2101111
    X3100111
    X4100011
    X5100101
    X6100110
    б
    X1X2X3X4X5X6
    X1100111
    Q=X2111111
    X3101111
    X4100111
    X5100111
    X6100111
    в
    X1X2X3X4X5X6
    X1111111
    Q=X2010000
    X3011000
    X4111111
    X5111111
    X6111111
    files
    (1) а
    (2) б
    (3) в
    По матрицам смежности определить какие из графов являются полными.
    а
    11110
    01010
    00110
    00010
    11110
    b
    01010
    00011
    11000
    00101
    10100
    c
    11011
    11101
    01111
    10111
    11111
    d
    00000
    10000
    11000
    11100
    11110
    (1) а, b, d
    (2) b, d
    (3) d
    Для графа G = (X, A) , представленного на рисунке 1, описать матрицей смежности порожденный подграф {х1,х2,х3, ,х5, х7} files
    а
    X1X2X3X5X7
    X101000
    X200101
    X300001
    X500100
    X700100
    b
    X1X2X3X5X7
    X101000
    X200110
    X300010
    X500100
    X710010
    c
    X1X2X3X5X7
    X101000
    X200101
    X300011
    X500001
    X710100
    (1) c
    (2) b
    (3) а
    Методом Мальгранжа разбить граф, представленный матрицей смежности, на максимальные сильно связные подграфы
    X1X2X3X4X5X6X7X8
    X101000001
    X210101000
    X300011000
    X400000100
    X500100010
    X600010000
    X710001100
    X800000010
    (1) G1={x1, x2 , х7, х8 }, G2 = { х3, х4 }, G3 ={ х5 ,х6}
    (2) G1={x1, x2 , х3, х5, х7, х8 }, G2 = { х4, х6}
    (3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7, х8 }
    Построить орцепи максимальной длины из вершин D и B графа, изображенного на рисунке files
    (1) (B, C), (D, E) →​ (E, F) →​ →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, C)
    (2) (B, B) →​ (B, C), (D, E) →​ (E, F) →​ →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, B) →​ (B, C)
    (3) (B, B) →​ (B, C), (D, E) →​ (E, F) →​ →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, C)
    Если с помощью алгоритма Дейкстры требуется найти кратчайшие пути от вершины x3 до других вершин графа, то в первой итерации ей присваивается пометка со значением ...
    (1) 3
    (2) 0
    (3) равным количеству вершин графа
    (4) равным количеству ребер графа
    Какие дуги инцидентны вершине 2 в графе на рисунке?files
    (1) c
    (2) b, c, f
    (3) e, c, f
    Для графа G1, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х3,х4). Верно ли результат представлен матрицей смежности ниже? files
    X1X2X(3,4)X5
    X11
    X21
    X(3,4)1
    X511
    (1) неверно
    (2) верно
    Найти прямые многозначные отображения 2-го порядка для вершин х3 и х4 графа, показанного на рисунке files
    (1) Г+2 (х3) = {х1, х4, х5}, Г+2 (х4) = { х2, х4, х5, }
    (2) Г+2 (х3) = { х4, х5}, Г+2 (х4) = { х2, х4, х5, }
    (3) Г+2 (х3) = {х1, х4, х5}, Г+2 (х4) = { х2, х4 }
    Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х1 и х6. files
    (1) {х1, х2, х3, х4, х6, х7}
    (2) {х1, х2, х3, х4, х7}
    (3) {х1, х2, х5, х4 }
    Какие из приведенных на рисунке графов являются симметрическими?files
    (1) a, с
    (2) а, c, d
    (3) a
    Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где xi,xj ∈X тогда и только тогда, когда i+j четно files
    (1) G = (Х, А), где X – множество вершин; А = {ai }, i = 1, 2, ..., 5– множество дуг, причем А = {(х7, х5), (х5, х3), (х3, х5 ), (х4, х6), (х6, х4), (х7, х1) }
    (2) G = (Х, А), где Х = {хi}, i = 1, 2, …,8– множество вершин; А = {ai }, i = 1, 2, ..., 7– множество дуг, причем А = {(х1, х3), (х2, х4), (х2, х6 ), (х3, х5), (х1, х7), (х8 , х6), (х7 , х1) }
    (3) G = (Х, А), где Х = {хi}, i = 1, 2, …,8 – множество вершин; А = {ai }, i = 1, 2, ...– множество дуг, причем А = {(х1, х3), (х2, х4), (х2, х6 ), (х2, х8), (х3, х5), (х3 , х7), (х4 , х6), (х6, х8) }
    Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного матрицей смежности
    X1X2X3X4X5X6X7X8
    X111100000
    X210100010
    X300001000
    X400110000
    X500011000
    X600000100
    X701000101
    X810101000
    (1) G1={x1, x2 , х7, х8 }, G2 = { х3, х4, х5 }, G3 ={х6}
    (2) G1={x1, x2 , х7, х8 }, G2 = { х3, х4 }, G3 ={ х5 ,х6}
    (3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7, х8 }
    Построить простые орцепи максимальной длины из вершин A и D графа, изображенного на рисунке files
    (1) (A, B) →​ (B, C), (D, E) →​ (E, F) →​ (F, A) →​ (A, B) →​ (B, C)
    (2) (A, B) →​ (B, C), (D, E) →​ (E, F) →​ (F, A) →​ (A, B) →​ (B, B) →​ (B, C)
    (3) (A, B) →​ (B, B) →​ (B, C), (D, E) →​ (E, F) →​ (F, A) →​ (A, B) →​ (B, C)
    Найти кратчайший путь от вершины 1 к вершине 6 графа, представленного на рисунке files
    (1) 8
    (2) 13
    (3) 15
    Какие дуги являются петлями в графе на рисунке?files
    (1) a, c
    (2) f, c
    (3) c, a, d, e
    (4) f
    Для графа G2, показанном на рисунке 1, выполнить операцию стягивания двух вершин (х3,х4). Верно ли результат представлен матрицей смежности ниже?files
    X1X2X(3,4)X5
    X11
    X2111
    X(3,4)11
    X5
    (1) неверно
    (2) верно
    Найти обратные многозначные отображения 4-го порядка для вершин х1 и х2 графа, показанного на рисунке files
    (1) Г-4 (х1) = { х2 ,х5 }, Г-4 (х2) = {х5 }
    (2) Г-4 (х1) = { х2}, Г-4 (х2) = {х5 }
    (3) Г-4 (х1) = { х2}, Г-4 (х2) = {х5 , х1}
    Для графа, данного на рисунке найти количество путей длиной 2 между всеми вершинами графа.files
    (1) 8
    (2) 18
    (3) 13
    Какие из приведенных на рисунке графов являются полными симметрическими?files
    (1) а, b, c
    (2) b, с
    (3) все
    Найти максимальный сильно связанный подграф, включающий вершину Е, для графа, матрица смежности которого представлена ниже
    ABCDEFGK
    A11001000
    B00101100
    C00101000
    D00000001
    E00000100
    F10000010
    G00000001
    K00010000
    (1) Gмсс={ B, C, E, F}
    (2) Gмсс={A, B, C, E, F}
    (3) Gмсс={A, B, E, F}

    Для графа на рисунке даны маршруты из вершины A в вершину F:files

    a) (A, B), (B, C), (C, G), (G, F)

    b) (A, K), (K, H), (H, F)

    c) (A, C), (C, E), (E, D), (D, C), (C, H), (H, F)

    d) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

    Найти среди них простые цепи

    (1) a, c
    (2) a, b
    (3) a, b, c
    Найти кратчайший путь от вершины x1 к вершине x10 графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Б files
    (1) 15
    (2) 16
    (3) 18
    Найдите полустепени исхода и захода для вершины х3 графаfiles
    (1) d0(х3)=3, dt(х3)=2
    (2) d0(х3)=1, dt(х3)=2
    (3) d0(х3)=2, dt(х3)=1
    В графе G6 , показанном на рис. 1 удалить вершину х2. Результат представлен в матричном виде ниже files
    а
    X2X3
    X201
    X210
    б
    X1X2
    X101
    X210
    в
    X1X3
    X101
    X310
    (1) верно б
    (2) верно а
    (3) верно в
    Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х3 и х4 files
    (1) Т+(х1) = { х1, х2, х3}, Т+( х2) ={ х1, х2, х3, х5, х6}
    (2) Т+(х1) = { х1, х3 }, Т+( х2) ={ х1, х2, х3, х5, х6}
    (3) Т+(х3) = { х3}, Т+( х4) ={ х1, х2, х3, х4, х5, х6}
    Для графа, данного на рисунке найти количество путей длиной 3 между всеми вершинами графа.files
    (1) 13
    (2) 9
    (3) 11
    Какие из приведенных на рисунке графов являются полными симметрическими?files
    (1) а, b, c
    (2) b, с
    (3) b
    Какие из приведенных на рисунке графов являются односторонне связными?files
    (1) d, e
    (2) a, d
    (3) e

    На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна. filesvn=∑ ai / ∑ bi

    (1) A →​ D →​ B →​ C →​ E →​ A
    (2) A →​ B →​ C →​ E →​ D →​ B
    (3) A →​ B →​ C →​ D →​ E →​ A
    (4) A →​ C →​ E →​ D →​ B →​ A
    Для графа, представленного на рисунке 1а, построить базу относительно вершины х7.filesfiles
    (1) рис. 2a
    (2) рис. 2b
    (3) рис. 2c
    Для графа, изображенного на рисунке, дать описание с помощью отображений files
    (1) G = (X, Г)) , где X = {хi}, i = 1, 2, ..., 4 – множество вершин, Г(х1)= , Г(х2) ={ х1, х4 }, Г(х3) = { х1, х3 }, Г(х4) = { х1 } – отображения
    (2) G = (X, Г)) , где X = {хi}, i = 1, 2, ..., 4 – множество вершин, Г(х2) ={ х1, х4 }, Г(х3) = { х1, х3 }, Г(х4) = { х1 } – отображения
    (3) G = (X, Г)) , где X = {хi}, i = 1, 2, ..., 4 – множество вершин, Г(х1)= , Г(х2) ={ х1, х4 }, Г(х3) = { х1}, Г(х4) = { х1 } – отображения
    В графе G6 , показанном на рис. 1 удалить дугу (х1,х2). Результат представлен ниже в матричном виде files
    а
    X1X2X3
    X111
    X211
    X31
    б
    X1X2X3
    X11
    X211
    X311
    в
    X1X2X3
    X11
    X211
    X311
    (1) верно б
    (2) верно а
    (3) верно в
    Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х3 и х4files
    (1) Т-(х3) = { х3, х2, х4, х1, х5}, Т-( х4) ={ х4 }
    (2) Т-(х3) = { х2, х4, х1, х5}, Т-( х4) =⊕
    (3) Т-(х3) = { х3, х2, х4, х1, х5}, Т-( х4) = ⊕
    Для графа, данного на рисунке найти между какими вершинами наибольшее число путей длиной 4.files
    (1) между B и A
    (2) между A и C
    (3) между D и C
    (4) между D и B
    Является ли граф на рисунке двудольным? files
    (1) да
    (2) нет
    Выделить в графе на рисунке e сильную компоненту, содержащую максимальное число элементов. files
    (1) < х1, х2, х4, х5 >
    (2) < х1, х2, х3, х4, х5 >
    (3) < х2, х4, х5 >
    files

    Для графа, представленного на рисунке даны замкнутые пути:

    М1: (х2, х3), (х3, х4), (х4, х7), (х7, х2)

    М2: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2) (х2, х3), (х3, х7), (х7, х2)

    М3: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2)

    М4: (х3, х4), (х4, х5), (х5, х7), (х7, х3)

    М5: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х1)

    М6: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6) (х6, х1)

    М7: (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6), (х6, х1), (х1, х2)

    Какие из этих путей являются гамильтоновыми контурами?

    (1) гамильтоновыми контурами являются: М6, М7
    (2) гамильтоновыми контурами являются: М4, М6
    (3) гамильтоновыми контурами являются: M2, М4, М6, М7
    Для графа, представленного на рисунке, дана матрица инциденций. Верно ли представлен граф?files
    матрица инциденций
    a1a2a3a4a5a6a7
    X1011000-1
    X20-10-1100
    X30000-1-10
    X400-11011
    (1) верно
    (2) не верно
    Является ли граф, представленный на рисунке, планарным? files
    (1) да
    (2) нет
    Выделить в графе на рисунке а одностороннюю компоненту, содержащую максимальное число элементов. files
    (1) < х2, х3, х4, х5>
    (2) < х2, х3, х4 >
    (3) < х1, х3, х4 >
    Для графа, представленного на рисунке построить гамильтоновы и эйлеровы циклы. files
    (1) гамильтонов цикл отсутствует, эйлеров цикл – (х1, х2), (х2, х3), (х3, х4), (х4, х6), (х6, х5), (х5, х1)
    (2) гамильтоновы циклы:(х1, х2), (х2, х3), (х3, х4), (х4, х6), (х6, х5), (х5, х1) или (х5, х1), (х1, х2), (х2, х3), (х3, х4), (х4, х6), (х6, х5); эйлеров цикл отсутствует
    (3) гамильтонов цикл:(х1, х2), (х2, х3), (х3, х4), (х4, х6), (х6, х5), (х5, х1) ; эйлеров цикл: (х5, х1), (х1, х2), (х2, х3), (х3, х4), (х4, х6), (х6, х5)
    По матрице смежности, данной ниже подсчитать полустепень исхода второй вершины do(х2)
    101100
    010101
    000101
    001001
    100000
    010001
    (1) d0(х2)=2
    (2) d0(х2)=3
    (3) d0(х2)=-2
    Для графа на рисунке найти сильную компоненту, содержащую элемент х5files
    (1) G2 = { х3, х5}
    (2) G2 = { х3, х4, х5}
    (3) G2 = { х2, х3,х5}
    По матрице инциденций найти полустепени захода для Х2
    a1a2a3a4a5a6a7a8a9a10
    X12-110101000
    X201-11000000
    X3000-1-110100
    X4000000-1-110
    X500000000-1-1
    X600000-10001
    (1) dt(х2)=2
    (2) dt(х2)=3
    (3) dt(х2)=1
    Является ли граф, изображенный на рисунке смешанным графом?files
    (1) не является
    (2) является
    Выполнить операцию нахождения кольцевой суммы G1 G2 для графов, показанных на рисунке 1files files files
    (1) граф представлен на рис.2 в
    (2) граф представлен на рис.2 б
    (3) граф представлен на рис.2 а
    Найти прямые отображения для вершин х5 и х6графа, показанного на рисунке files
    (1) Г+1 (х5) = {х2 }, Г+1 (х6) = {х1, х5 }
    (2) Г+1 (х5) = {х2 }, Г+1 (х6) = {х1, х3 }
    (3) Г+1 (х5) = {х5 }, Г+1 (х6) = {х1, х5 }
    Для графа, представленного на рисунке построить матрицу достижимости и определить для какой из вершин графа достижимо наибольшее число вершин.files
    (1) Х1
    (2) Х2
    (3) Х1 и Х2
    Какие из приведенных на рисунке графов являются полными?files
    (1) а, с, d
    (2) c
    (3) а, с
    Дан граф на риунке 1. Какой из приведенных на рисунке 2 графов является для него порожденным подграфом?filesfiles
    (1) a
    (2) b
    (3) с
    (4) d
    (5) ef
    (6) f
    Методом Мальгранжа разбить граф, представленный на рисунке, на подграфыfiles
    (1) G1={x1, x2 , х7, х8 }, G2 = { х3, х4, х5 }, G3 ={х6}
    (2) G1={x1, x2 , х7, х8 }, G2 = { х3, х4, х6 }, G3 ={х5}
    (3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7, х8 }
    Построить все возможные пути длиной 2 в графе, изображенном на рисунке для вер­шин E и Bfiles
    (1) E →​ F →​ A, E →​ B →​ B, E →​ B →​ C, E →​ F →​ D, B →​ В →​ C
    (2) E →​ F →​ A, E →​ B →​ C, E →​ F →​ D
    (3) E →​ F →​ A, E →​ B →​ C, E →​ F →​ D, B →​ В →​ C
    Обновление пометок на каждой итерации алгоритма Дейкстры происходит
    (1) для вершин графа, имеющих временные метки и входящих в прямое отображение для рассматриваемой вершины
    (2) для всех вершин графа
    (3) для вершин графа, имеющих временные метки
    Какие вершины инцидентны дуге b в графе на рисунке?files
    (1) 1, 2
    (2) 2
    (3) 1, 2, 3
    Выполнить операцию нахождения кольцевой суммы G1 ⊕ G2 для графов, представленных матрицами смежности в таблице 1
    Матрица смежности G1
    X1X2X3X4X5
    X100001
    X210010
    X300000
    X400100
    X501010
    Матрица смежности G2
    X1X2X3X4X5
    X100001
    X210101
    X300000
    X401101
    X500000
    a
    X1X2X3X4X5
    X100001
    X210000
    X300000
    X400100
    X500000
    б
    X1X2X3X4X5
    X100000
    X200111
    X300000
    X401001
    X501010
    в
    X1X2X3X4X5
    X100001
    X210111
    X300000
    X401101
    X501010
    (1) граф представлен б
    (2) граф представлен а
    (3) граф представлен в
    Найти обратные отображения для вершин х1и х2графа, показанного на рисунке files
    (1) Г–1 (х1) = { х2 }, Г–1 (х2) = {х5 }
    (2) Г–1 (х1) = { х1, х2, х6}, Г–1 (х2) = { х1, х5 }
    (3) Г–1 (х1) = { х2 , х6}, Г–1 (х2) = {х5 , х1}
    Для графа, представленного на рисунке построить матрицу контрдостижимости и определить какая из вершин достижима для наибольшего числа вершин графа.files
    (1) Х1
    (2) Х4
    (3) Х2
    По матрицам смежности определить какие из графов являются полными.
    а
    1111
    0011
    0001
    0000
    b
    0101
    0001
    0010
    1010
    c
    1010
    1101
    0111
    0111
    d
    1010
    1100
    0110
    1010
    (1) а, c, d
    (2) a
    (3) a, с
    Для графа G = (X, A) , представленного на рисунке 1, описать матрицей смежности порожденный подграф {х2,х3, х4,х5, х6} files
    а
    X2X3X4X5X6
    X201010
    X300110
    X400001
    X501000
    X600100
    b
    X2X3X4X5X6
    X201000
    X300110
    X400100
    X500010
    X610010
    c
    X2X3X4X5X6
    X201000
    X300101
    X400001
    X501001
    X610100
    (1) b
    (2) c
    (3) a
    Методом Мальгранжа разбить граф, представленный на рисунке, на максимальные сильно связные подграфыfiles
    (1) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х4, х7, х8 }
    (2) G1={x1, x2 , х3, х5 , х7, х8 }, G2 ={ х4 , х6}
    (3) G1={x1, x2 , х8 }, G2 = { х3, , х7, х5 }, G3 ={х6 , х4}
    Построить орцепи максимальной длины из вершин E и F графа, изображенного на рисунке files
    (1) (E, F) →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, C), (F, D) →​
    (2) (E, F) →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B,B) →​ (B, C), (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, B) →​ (B, C)
    (3) (E, F) →​ (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, C), (F, D) →​ (D, F) →​ (F, A) →​ (A, B) →​ (B, C)
    Значение постоянной метки показывает
    (1) значение среднего пути
    (2) значение кратчайшего пути
    (3) число итераций
    Какие дуги инцидентны вершине 1 в графе на рисунке?files
    (1) b, e
    (2) a
    (3) a, b, d, e
    Для графа G1, показанном на рисунке 1, выполнить операцию отождествления двух вершин (х3,х4). Верно ли результат представлен на рис. 2а? files files
    (1) неверно
    (2) верно
    Найти прямые многозначные отображения 3-го порядка для вершин х5 и х6 графа, показанного на рисунке files
    (1) Г+3(х5) ={ х1, х2, х3, х4, х6}, Г+3(х6) ={ х1, х2, х3, х4, х5, х6}
    (2) Г+3(х5) ={ х1, х2, х3, х4, х6}, Г+3(х6) ={ х2, х3, х4, х5, х6}
    (3) Г+3(х5) ={ х1, х2, х3, х4, х5, х6}, Г+3(х6) ={ х1, х2, х3, х4, х5}
    Для графа, представленного на рисунке, найти: вершины, входящие в путь между вершинами х1и х3. files
    (1) {х1, х2, х3, х7}
    (2) {х1, х2, х3, х4 , х7}
    (3) {х1, х2, х3, х4}
    Какие из приведенных на рисунке графов являются симметрическими? files
    (1) а, b, d
    (2) a, b
    (3) b
    Для графа G = (X, A) , представленного на рисунке, описать явно остовный подграф(X, A’) , где xi,xj ∈ A' тогда и только тогда, когда i+j < 10files
    (1) G = (Х, А), где Х = {хi}, i = 1, 2, …, 8 – множество вершин; А = {ai }, i = 1, 2, ..., 7– множество дуг, причем А = {(х1, х2), (х4, х5), (х2, х4 ), (х2, х3), (х3, х5), (х4 , х1), (х7 , х1), }
    (2) G = (Х, А), где Х = {хi}, i = 1, 2, …,8– множество вершин; А = {ai }, i = 1, 2, ...7 – множество дуг, причем А = {(х1, х2), (х1, х8), (х2, х3 ), (х2, х5), (х3, х5), (х5 , х3), (х3 , х4), (х7 , х1) }
    (3) G = (Х, А), где Х = {хi}, i = 1, 2, …,8 – множество вершин; А = {ai }, i = 1, 2, ..., 7 – множество дуг, причем А = {(х1, х2), (х2, х3), (х2, х5 ), (х3, х4), (х1, х8), (х1 , х7), (х5 , х3), }
    Метод разбиения графа по матрицам R и Q рассмотреть на примере графа, изображенного матрицей смежности
    X1X2X3X4X5X6X7X8
    X111010000
    X210101010
    X300001000
    X400110000
    X500011000
    X600000100
    X701100101
    X810000001
    (1) G1={x1, x2 , х7, х8 }, G2 = { х3, х4 }, G3 ={ х5 ,х6}
    (2) G1={x1, x2 , х7, х8 }, G2 = { х3, х4, х5 }, G3 ={х6}
    (3) G1={x1, x2 }, G2 = { х3, х4, х5 }, G3 ={х6, х7, х8 }
    Построить простые орцепи максимальной длины из вершин F и E графа, изображенного на рисунке files
    (1) (E, F) →​ (F, A) →​ (A, B) →​ (B, B) →​ (B, C), (F, A) →​ (A, B) →​ (B, C)
    (2) (E, F) →​ (F, A) →​ (A, B) →​ (B, C), (F, A) →​ (A, B) →​ (B, C)
    (3) (E, F) →​ (F, A) →​ (A, B) →​ (B, C), (F, A) →​ (A, B) →​ (B, B) →​ (B, C)
    Найти кратчайший путь от вершины 1 к вершине 8 графа, представленного на рисунке files
    (1) 16
    (2) 19
    (3) 13
    Какие дуги являются петлями в графе на рисунке ?files
    (1) d
    (2) d и f
    (3) c и b
    Для графа G2, показанном на рисунке a, выполнить операцию стягивания двух вершин (х3,х4). Верно ли результат представлен графом на рисунке б?files
    (1) неверно
    (2) верно
    Найти обратные многозначные отображения 4-го порядка для вершин х5 и х3графа, показанного на рисунке files
    (1) Г-4 ( х5) ={ х1, х4 }, Г-4 ( х3)={х2 , х5 , х1}
    (2) Г-4 ( х5) ={ х1, х4 }, Г-4 ( х3)={х2 }
    (3) Г-4 ( х5) ={ х1, х4 }, Г-4 ( х3)={х2 ,х1 }
    Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: F и C или D и Bfiles
    (1) одинаковое количество
    (2) между D и B
    (3) между F и C
    Какие из приведенных на рисунке графов являются антисимметрическими?files
    (1) а, b, d
    (2) a,b,c
    (3) a, с
    Найти максимальный сильно связанный подграф, включающий вершину F, для графа, матрица смежности которого представлена ниже
    ABCDEFGK
    A11001000
    B00101100
    C00101000
    D00000001
    E00000100
    F10000010
    G00000001
    K00010000
    (1) Gмсс={ B, C, E, F}
    (2) Gмсс={A, B, C, E, F}
    (3) Gмсс={A, B, E, F}

    Для графа на рисунке даны маршруты из вершины A в вершину F:files

    a) (A, B), (B, C), (C, F)

    b) (A, K), (K, H), (H, F)

    c) (A, K), (K, H), (H, C), (C, K), (K, H), (H, F)

    Найти среди них цепи

    (1) a, b, c
    (2) a, b
    (3) a
    Найти кратчайший путь от вершины x1 к вершине x9 графа, представленного на рисунке А, матрица расстояний между вершинами дана на рис. Бfiles
    (1) 21
    (2) 12
    (3) 10
    Найдите полустепени исхода и захода для вершины х1 (вершина обзначена на рисунке цифрой 1) графаfiles
    (1) d0(х1)=3, dt(х1)=2
    (2) d0(х1)=2, dt(х1)=2
    (3) d0(х1)=2, dt(х1)=1
    В графе G6 , показанном на рис. 1 удалить вершину х3. Результат представлен в матричном виде ниже files
    а
    X2X3
    X201
    X210
    б
    X1X2
    X101
    X210
    в
    X1X3
    X101
    X310
    (1) верно б
    (2) верно а
    (3) верно в
    Для графа, изображенного на рисунке найти прямые транзитивные замыкания для вершин х5и х6,files
    (1) Т+(х5) = { х1, х2, х3, х5, х6}, Т+(х6) = { х6}
    (2) Т+(х5) = { х1, х2, х3, х5}, Т+(х6) = { х6}
    (3) Т+(х5) = { х1, х2, х3, х5, х6}, Т+(х6) = { х1, х2, х6}
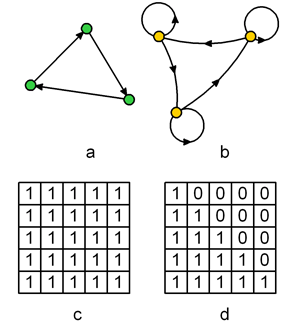
    Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: A и C или B и Dfiles
    (1) между Aи C
    (2) одинаковое количество
    (3) между B и D
    Какие из приведенных на рисунке графов являются полными антисимметрическими?files
    (1) а
    (2) a, d
    (3) все
    Какие из приведенных на рисунке графов являются слабо связными?files
    (1) b, f
    (2) b, c, f
    (3) c, f
    На рисунке дан граф со взвешенными дугами, который представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку(a, b), причем а равно выгоде, получаемой при обслуживании этого маршрута, а b – времени обслуживания маршрута. Найти, какой из перечисленных путей наиболее выгодный (в терминах скорости оборота капитала) путь судна. filesvn=∑ ai/ ∑ bi
    (1) A →​ B →​ C →​ D →​ E →​ A
    (2) A →​ B →​ C →​ E →​ D →​ B
    (3) A →​ D →​ B →​ C →​ E →​ A
    Для графа, представленного на рисунке 1а, построить базу относительно вершины х3.filesfiles
    (1) рис. 2b
    (2) рис. 2a
    (3) рис. 2c
    Для files графа, изображенного на рисунке, дано описание с помощью отображений. G = (X, Г) , где X = {хi}, i = 1, 2, 3, 4 – множество вершин, Г(х1)= , Г(х2) ={ х1, х4 }, Г(х3) = { х1, х3 }, Г(х4) = { х1 } – отображения. Верно ли оно?
    (1) не верно
    (2) верно
    В графе G6 , показанном на рис. 1 удалить дугу (х1,х3). Результат представлен ниже в матричном виде files
    а
    X1X2X3
    X111
    X211
    X31
    б
    X1X2X3
    X11
    X211
    X311
    в
    X1X2X3
    X11
    X211
    X311
    (1) верно б
    (2) верно а
    (3) верно в
    Для графа, изображенного на рисунке найти обратные транзитивные замыкания для вершин х1 и х2,files
    (1) Т-(х1) = { х1, х2, х3, х4, х5 }, Т-(х2) ={ х1, х2, х4, х5 }
    (2) Т–(х1) = { х1, х2, х4, х5 }, Т-(х2) ={ х1, х2, х3, х4, х5 }
    (3) Т-(х1) = { х1, х2, х4, х5 }, Т-(х2) ={ х1, х2, х4, х5 }
    Для графа, данного на рисунке определить между какой парой вершин большее количество путей длиной 2: F и C или E и Cfiles
    (1) между F и C
    (2) одинаковое количество
    (3) между E и C
    Является ли граф на рисунке двудольным? files
    (1) нет
    (2) да
    Выделить в графе на рисунке f сильную компоненту, содержащую максимальное число элементов. files
    (1) < х3, х2, х4, х5 >
    (2) < х2, х4, х5 >
    (3) < х2, х5 >
    files

    Для графа, представленного на рисунке даны замкнутые пути:

    М1: (х2, х3), (х3, х4), (х4, х7), (х7, х2)

    М2: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2) (х2, х3), (х3, х7), (х7, х2)

    М3: (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х2)

    М4: (х3, х4), (х4, х5), (х5, х7), (х7, х3)

    М5: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х6), (х6, х1)

    М6: (х1, х2), (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6) (х6, х1)

    М7: (х2, х3), (х3, х4), (х4, х5), (х5, х7), (х7, х6), (х6, х1), (х1, х2)

    Какие из этих путей являются эйлеровыми контурами?

    (1) эйлеровыми контурами являются M2, М7
    (2) эйлеровыми контурами являются М4, М6
    (3) эйлеровых контуров нет
    Даны матрицы смежности и матрица инцидентности. Соответствуют ли они графу на рисунке?files
    матрица смежности
    X1X2X3X4
    X11100
    X20011
    X30000
    X41110
    матрица инциденций
    a1a2a3a4a5a6a7
    X1011000-1
    X20-10-1100
    X30000-1-10
    X400-11011
    (1) соответствует матрица инцидентности
    (2) не соответствуют обе матрицы
    (3) соответствует матрица смежности
    Является ли граф, представленный на рисунке, планарным? files
    (1) да
    (2) нет
    Выделить в графе на рисунке f одностороннюю компоненту, содержащую максимальное число элементов. files
    (1) < х1, х2, х4,х5 >
    (2) < х1, х4, х5 >
    (3) < х1,х2, х3, х4,х5 >
    Для графа, представленного на рисунке построить гамильтонов цикл и эйлеров путь. files
    (1) гамильтонов цикл: A →​ B →​ C →​ D →​ E →​ A; эйлеров цикл: B →​ C →​ D →​ A →​ B →​ D →​ E →​ A →​ C
    (2) гамильтонов цикл: A →​ B →​ D →​ C →​ A →​ E; эйлеров цикл: B →​ C →​ D →​ A →​ B →​ D →​ E →​ A →​ C
    (3) гамильтонов цикл: A →​ B →​ C →​ D →​ E →​ A; эйлеров цикл: A →​ B →​ C →​ D →​ A →​ C →​ B →​ D →​ E →​ A
    По матрице смежности, данной ниже подсчитать полустепень захода второй вершины dt(х2)
    101100
    010101
    000101
    001001
    100000
    010001
    (1) dt(х2)=2
    (2) dt(х2)=3
    (3) dt(х2)=-2
    Для графа на рисунке найти сильную компоненту, содержащую элемент х4files
    (1) G2 = { х4,х3}
    (2) G2 = { х4, х6}
    (3) G2 = { х4, х3,х6, х7}
    Соответствует ли матрица инциденций матрице смежности (обе матрицы представлены ниже):
    матрица инциденций
    a1a2a3a4a5a6a7a8a9a10
    X11-110101000
    X201-11000000
    X3000-1-110100
    X4000000-1-110
    X500000000-1-1
    X600000-10001
    матрица смежности
    X1X2X3X4X5X6
    X1111100
    X2101000
    X3000101
    X4000010
    X5000000
    X6000010
    (1) соответсвует только для неориентированного графа
    (2) не соответствует
    (3) соответсвует
    Для графа G1, показанном на рисунке a, выполнить операцию стягивания двух вершин (х1,х2). Верно ли результат представлен графом на рисунке б?files
    (1) неверно
    (2) верно
    Какие из приведенных на рисунке графов являются деревьями?files
    (1) а, b
    (2) a, с, d
    (3) все